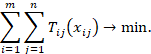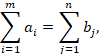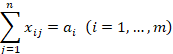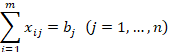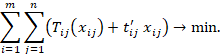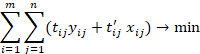Article
citation information:
Kowalik,
P., Stopka, O. Time minimization delivery planning with the time-quantity dependence. Scientific Journal of Silesian University of
Technology. Series Transport. 2025, 128,
95-114. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2025.128.6
Przemysław KOWALIK[1],
Ondrej STOPKA[2]
TIME MINIMIZATION
DELIVERY PLANNING WITH
THE TIME-QUANTITY DEPENDENCE
Summary. One of the classical
problems in transportation planning is represented minimizing the maximal
delivery time of a uniform commodity between sources and destinations, known as
the Bottleneck Transportation Problem (BTP). It assumes that a fixed transportation
time – independent of the quantity of the transported commodity – is assigned
to each source-to-destination route. In some cases, however, the quantity of
the transported commodity may affect the transportation time, e.g., because of
the duration of loading/unloading the commodity to/from the vehicle. Extensions
of the BTP as well as the closely related Total Time Minimization
Transportation Problem (TTMTP) which include the linear time-quantity
dependence of the delivery time are considered. Whereas similar optimization
problems known in the literature are nonlinear, linear programming is used in
this research. Linear optimization provides better performance of the
optimization software in comparison with nonlinear optimization. The above fact
is illustrated by improving solutions to the problems known in the literature.
A detailed insight into the issue of the existence of integer optimal solutions
and interpretations of optimal solutions is also provided.
Keywords: transport optimization, bottleneck transportation problem, total time
minimizing transportation problem, integer linear programming
1. INTRODUCTION AND LITERATURE REVIEW
Transportation is one of the most important
human activities, essential for businesses, public services, emergency aid, and
military operations. The optimization of transportation operations has always
been an interest of decision makers. However, the mathematical complexity of
many real-world problems is often an obstacle in the efficient search for
optimal solutions. The beginnings of the contemporary scientific approach to
transportation optimization date back to the second quarter of the 20th
century, when papers by Tolstoi [1],
Kantorovich [2]
and Hitchcock [3]
were published. Especially the problem considered by Hitchcock, known as the
Hitchcock Transportation Problem, the Standard
Transportation problem (STP), the Cost Minimization Transportation Problem
(CMTP) or just the Transportation Problem (TP) was a “starting point” in the
modern optimization of transport operations. It can be briefly described as the
allocation of a uniform commodity on the routes connecting sources with limited
supplies to destinations with defined demands. The goal of the allocation is to
minimize the total transportation (also referred to as shipping) cost while the
demands are satisfied, and the limits of supplies are not exceeded. Moreover,
the transportation cost on each route is the product of a fixed unit cost and
the amount of the commodity and the total transportation cost is the sum of the
costs on all routes, making the total transportation cost a multivariable
linear function. In 1951 Dantzig [4]
expressed the STP as a linear programming problem and solved it using the
simplex method. Because of a specific mathematical form of the STP which allows
for the use of computational techniques not available for “general” linear
programming problems, many various solving methods like the Stepping Stone
Method [5],
Vogel’s Approximation Method or VAM [6],
Least Cost Method or LCM [7],
modified Stepping Stone Method [8],
Lowest Allocation Method or LAM [9],
some modifications of Vogel’s Method [10-11]
have been developed.
Even though TP was itself a great achievement,
it turned out as early as in 1950’s that reliable modeling
the decisions related to the real-world transportation required more elaborate
mathematics, which resulted in creating many extensions of STP (see e.g. [13]).
In particular, minimization of the total cost (of the transportation itself
only or increased by some other costs) was no longer a unique criterion of
optimality used in extensions of STP.
Among the optimality criteria other than the
minimization cost, the time minimization is one of the most important ones.
This criterion requires a more detailed description in the context of
optimization of transportation activities because it has two different meanings
under the same name. The first meaning is “to minimize the time in which the
commodity is delivered to all the destinations, assuming that the
transportation started simultaneously at all the sources”. This criterion is modeled under the names the Bottleneck/Time Minimizing
Transportation Problem. Another meaning can be “to minimize the total time in
which the transportation of the commodity is performed (the sum of the
transportation times on all routes connecting sources and destinations)”. The
latter criterion is modeled as the Total Time
Minimizing Transportation Problem.
The both meanings of “the time minimization”
refer to two separate time-related optimality criteria that occur instead of
the cost minimization criterion of STP (or some of its extensions) while the
constraints regarding the flow of the commodity remain unchanged. The first
criterion results from situations in which the time of completing the
deliveries, not the cost, matters, like deliveries of emergency supplies to
locations affected by disasters, ammunition to battlefields, perishable goods
to customers, etc. The second one results from the necessity of minimizing the
usage of scarce resources like the work time of drivers or plane/ship crews. To
continue, an important assumption must be made. Namely, for both of the
abovementioned criteria, it is assumed that there is a fixed transportation
time assigned to each source-destination pair, which does not depend on the
quantity of the transported commodity. A motivation for such an assumption is
that if a non-zero flow of the commodity is scheduled to a route, then the
commodity on this route is transported in a single vehicle or in a “team” of
vehicles traveling together (e.g., a single truck or a convoy of trucks). For
simplicity reasons, in later considerations we assume that if a positive
quantity of the commodity is transported, then a single vehicle is always used
for transportation on any source-to-destination route (and such a route is then
called “a used route”). When the time-optimization criteria are applied, the
time of the transportation on any specific route is a discontinuous function of
the quantity of the commodity, which equals zero for the argument equal to zero
and equals a constant positive number for a positive argument.
The difference between the two abovementioned
criteria is the objective function. For the first one, it is the maximum of the
transportation times over all the routes, whereas for the second one, it is the
sum of the transportation times over all the routes. The first case is more
represented in the literature, and it is known as the Bottleneck Transportation
Problem (BTP) or the Time Minimizing Transportation Problem (TMTP). The second
problem is known as the Total Time Minimizing Transportation Problem (TTMTP).
The earliest time-optimal version of the problem
known today as BTP or TMTP was formulated by Barsov in 1959 [15],
who named it the Transportation Problem Time with a Time Criterion. Further
developments in solving BTP are due to Nesterov [16],
Grabowski [17,18]
(as the Transportation Problems with Minimal Time), Szwarc [19,20] (as the Time Transportation Problem) and Hammer (as the Time
Minimizing Transportation Problem) [21]. All those authors used modifications of the simplex
method to solve the problem. Garfinkel and Rao in [22] used an approach based on the Hungarian method
instead. Garfinkel and Rao were also the first ones to use the name “Bottleneck
Transportation Problem”. More progress was achieved by Sharma and Swarup [23],
Bhatia, Swarup and Puri [24],
Seshan and Tikekar [25], Issermann [26].
Another approach to solving BTP is to consider it as a special case of
so-called bottleneck linear programming [27].
BTP allowed to model decisions that were
impossible to be handled by STP. BTP in its “pure” form, however, also turned
out not to be sufficient for modeling some real-world
decisions, and this is why many extensions of BTP have been created in response
to the needs of decision-makers. Those extensions included the Capacitated
Bottleneck Facility Location Problem [28],
the Bottleneck Capacitated Transportation Problem with Bounds on Rim Conditions
[29],
the Time Minimizing Transportation Problem with Mixed Constraints [30].
The time optimization in transportation planning
does not need to occur instead of the cost optimization as a unique criterion
of optimality. They may “coexist”, being both – not necessarily equally –
important to a decision maker. This is why some models that consider both
optimality criteria have also been created. In [31]
the Bottleneck-Cost Transportation Problem was introduced as a bi-criteria
optimization problem in which the total cost and the delivery time are
minimized simultaneously. In [32]
two complementary bi-level programming models are considered in which either minimizing the maximal
delivery time is the primary and minimizing the cost is the second-level
optimality criterion or vice versa. In [33]
the Constrained Bottleneck Transportation Problem (CBTP) was introduced, in
which a budget constraint (the maximal total transportation cost) was added.
Dropping the assumption of the lack of
dependence of the transportation time on the actual quantity of the transported
commodity, which is a main issue investigated in this paper, has also been
considered but to a limited extent only. In [34]
such a dependence was introduced as an increasing
piecewise constant function. This dependence resulted from the necessity of
performing multiple trips for each source-destination pair due to insufficient
capacities of the available vehicles. A version of BTP with the transportation
time being proportional to the quantity of the delivered commodity instead of
the fixed time was considered in [33].
The quantity-dependent and fixed components of the delivery time were joined
together into one model in [35]
and [36].
In those papers, the unloading time proportional to the amount of the delivered
commodity, added to the fixed time was considered. In [36]
the standard BTP model was extended by including both the loading and unloading
time and also by considering using many vehicles per route because of the
limited availability of vehicles. In this paper the concepts of the
time-quantity dependence from [35],
[36] and
[36]
are joined together and extended into one mathematical model (without multiple
vehicle usage considered in [36],
however).
This paper is intended to present a
comprehensive theoretical background and to provide an efficient computational
method for the transportation problem with the time minimization and the
time-quantity dependence. Whereas this paper is devoted mainly to an extension
of BTP that includes the time-quantity dependence, an analogical extension of
TTMTP is also considered. Particular goals of the paper are the following.
The first goal is to formulate an extension of
BTP to the case in which the minimal delivery time depends also on the quantity
of the transported commodity, based on the research in the field. This
extension concerns a wider range of practical applications of the model than
those defined in [35]
and [36],
but without changing its mathematical form. A new name for the considered
problem is also introduced to better conform to the existing naming conventions
in the field. An analogical extension of TTMTP (based on [38])
is also introduced.
The second and most important goal is to
reformulate the proposed extension of BTP which is, like the “pure” BTP, a
nonlinear optimization problem, to be a linear optimization problem. The reason
for the reformulation is practical. Whereas the linear formulation of the
considered problem is formally equivalent to the nonlinear one, the performance
of optimization software may be poor in the case of nonlinear optimization,
resulting in calculating worse, suboptimal solutions instead of optimal ones.
This phenomenon occurred in [36].
Unfortunately, no efficient method of obtaining optimal solutions was presented
or even suggested. In this paper it was shown that optimizing a linear version
of the considered problem allows finding an optimal solution. An analogical
linearization of the extension of TTMTP is also performed.
The third goal is to discuss the existence of
integer-valued optimal solutions of the considered optimization problems
depending on the values of the parameters, as well as the necessity of imposing
integer constraints on the variables.
The paper has the following structure. Section 2
reviews BTP and TTMTP as formulated nonlinear programming problems and presents
their extensions, which include a component of the delivery time depending on
the quantity of the transported commodity. Those extensions, primarily
nonlinear, are later reformulated as linear programming problems. The issues
related to integer-valued optimal solutions are also discussed. In Section 3,
two example problems, one from [35]
and one from [36],
are solved as linear programming problems to show the improvement in the
quality of the solutions obtained thanks to using linear optimization instead
of nonlinear. The results of other calculations related to the existence of
integer optimal solutions. Section 5 contains a discussion on the considered
models themselves as well as on the results of the performed calculations. In
Section 6, final conclusions are presented.
2. DATA AND
METHODS
The
main topic of this section is an extension of BTP with the quantity-time
dependence and its linearization. An analogical extension and linearization
will be performed on TTMTP.
Let
us introduce the necessary notation, common to BTP and TTMTP, and their
extensions. A uniform commodity is to be delivered from 
sources to 
destinations. The transportation time for each
“source-destination” pair is constant and does not depend on the amount of the
commodity. However, if no commodity is transported, then the transportation
time is obviously equal to zero. Each “source-destination” pair is called a route
from source 
to destination 
. The following
parameters are given:
·
– maximal possible
supply from source 
·
– demand of destination 
;
·
– transportation
time of any non-zero quantity of the commodity from source to destination 
;
·
– the maximal
capacity of the route from source to destination (optional
parameters) .
The variables
denote quantities of the commodity through all the routes:
·
– amount of the
commodity transported from source to destination .
The
above parameters and variables are identical to those in the STP except for 
.
On the other hand, no cost-related parameters occur in BTP and TTMTP. The
interpretation of can be just as simple as “the trip time from 
to ”.
An assumption is also made that the delivery on each route is performed by a
single vehicle. The value includes the “true” time in motion (the
driving time), but it can also include time required for the rest or refueling or any other inevitable breaks.
Finally,
the delivery time of any (zero or positive) quantity of the commodity from
source to destination can be then expressed as the following
conditional formula:
|
|
(1) |
The
goal of transportation planning in the BTP model is to complete the deliveries
of the commodity as soon as possible, assuming that they start simultaneously
from all the sources. In other words, the latest time of completing all the
deliveries is calculated. Alternatively, the goal can be formulated as all the
deliveries must reach their destinations simultaneously, and the earliest start
time of some deliveries is calculated. This goal means that, no matter if for
the latest time of completing or the earliest start time, the maximum of 
over all 
must be minimized. Finally, the objective
function of BTP is the following:
|
|
(2) |
The
only difference between TTMTP and BTP is the objective function, which in TTMTP
is just the sum of the transportation times on all the routes:
|
|
(3) |
Both BTP and TTMTP share the same
set of constraints, initially introduced in STP. For simplicity of the
notation, we also assume additionally that the problem under consideration is
balanced, i.e., the sum of all the maximal possible supplies (the total maximal
possible supply) is equal to the sum of all the demands (the total demand):
|
|
(4) |
Both
objective functions (2) and (3) are subject to the constraints:
|
|
(5) |
|
|
|
|
|
(6) |
|
|
|
|
|
(7) |
|
|
|
|
|
(8) |
Constraints (8) are imposed only if it is necessary,
i.e., if there are upper bounds on the capacities of the routes. The details of
using (8) will be discussed later.
A
remark on integer solutions is necessary. A well-known property of STP
concerning the existence of integer-valued optimal solutions is now reminded.
If all the parameters 
,
and, if defined, 
are integer, then the constraints (5-8) define
a feasible set in which that all the basic feasible solutions (the coordinates
of the corner points of the feasible set) are all integer. In this case, the
optimal solutions (one or more) are also integer because they are found among
the basic feasible solutions. This property is not restricted to STP, however,
it holds also for BTP and TTMTP, as explained below.
In
[39]
it was proved that the objective function of BTP (2) is a concave function, and
due to the concavity of the objective function, the search for an optimal
solution is restricted to the set of the basic feasible solutions only. Thus,
if 
and, if defined, 
in
BTP are all integer, then the basic feasible solutions, and what follows, also
optimal solutions are integer. This is why there is no need to impose integer
constraints on .
As
to TTMTP, it is mathematically equivalent to the Pure Fixed Charge
Transportation Problem (PFCTP) [40]
in which the fixed cost parameters are replaced with the time parameters .
PFCTP itself is a special case of the Fixed Charge Transportation Problem
(FCTP) [41],
[42].
One of the basic properties of all the linear fixed charge problems is that the
optimum is attained at a corner point of the feasible set of the continuous
variables [42].
So again, if and, if defined, in
TTMTP are all integers, then the basic feasible solutions and optimal solutions
are also integer.
Both BTP and TTMTP, even though useful
in many real-world applications, may be, in some circumstances, too simple to
meet the needs of decision makers. In particular, they do not take into account
the fact that the delivery process on any route may depend on the quantity of
the commodity (obviously besides the dependence “zero time for no
commodity/fixed time for a positive quantity of the commodity”). As it
previously mentioned, this dependence was considered in [35] and [36] as the
unloading time and in [36]
as both the loading and unloading times. In all the above cases, loading and
unloading times were assumed to be proportional to the quantity of the
delivered commodity on each route. However, it is easy to notice that the
abovementioned dependencies can be interpreted in a wider sense than that
formulated in [35], [36] and [36]. Namely, it is not loading and unloading times
only that sometimes must be included in the total delivery time. There can also
be a possible increase in the transportation time itself caused by slowing down
the vehicle carrying the heavy load. The sum of the loading time, the unloading
time, and the transportation time increase, all of which depend on the quantity
of the transported commodity being transported, will be referred to as the quantity-dependent
time. The quantity-dependent time added to the quantity transportation time
gives the value of the actual delivery time.
The simplest way to include in an optimization process the quantity-time
dependence is to assume that the quantity-dependent time is proportional to the
quantity of the commodity. Obviously, loading and unloading times of the same
amount of commodity do not need to be equal. They may also differ at various
locations due to the availability of necessary equipment and staff. The
quantity-dependent transportation time increase may also be different on
various routes, for example, because of various road quality.
Extensions
of BTP and TTMTP that include the quantity-dependent time into the optimization
criteria as described above
will be named the Quantity Dependent Bottleneck Transportation Problem (QDBTP)
and the Quantity Dependent Total Time Minimizing Transportation Problem
(QDTTMTP), respectively.
We
need to introduce the following additional parameters in order to extend the
previously considered models to QDBTP and QDTTMTP, respectively:
·
– the unit quantity-dependent time, i.e., the
sum of the times of loading and unloading one unit of the commodity on the
route from source 
to destination plus the increase of the transportation time
resulting from transporting one unit of the commodity on the route from source to destination 
.
The
assumption that the quantity-dependent time is proportional to the quantity of
the commodity means that the quantity-dependent time for a route connecting to is 
and the delivery time for that route is 
.
The parameters 
are used in the objective functions of QDBTP
and QDTTMTP only. However, they all share the same set of constraints,
initially introduced in STP (with one exception connected with integer
constraints in QDBTP, discussed later).
The
objective function for QDBTP is:
|
|
(9) |
The objective
function for QDTTMTP:
|
|
(10) |
Both (9) and (10) are subject to the constraints (5-8).
Whereas
the constraints (5-8) are linear, both objective
functions (9) and (10) are not linear and not smooth (see Figure 2). The lack
of linearity and smoothness of the objective functions (9) and (10) results
from nonlinearity of , 
.
Moreover in (9), nonlinear formulas are arguments for another nonlinear function
max.
The
calculations in [36] showed that optimizing the QDBTP models with the objective
function (9) (transformed, but still nonlinear) may lead to ambiguous,
suboptimal solutions. Instead, in this paper, a linearization, i.e., a
transformation of QDBTP into a linear programming problem, is considered.
Linearization of QDTTMTP is performed by using the same technique.
Linearization
described below consists of well-known transformations, applied to the two
considered objective functions.
The
first step is linearization of . Whereas
explicit constraints (8) restricting the route capacities in STP and, what
follows, in BTP/QDBTP and TTMTP/ QDTTMTP are optional, it does not mean that can attain arbitrarily large values. Instead,
implicit capacity constraints for all the routes exist. Indeed, by (5) and (6),
the quantity of the transported commodity on each route cannot exceed the
minimum of the maximal possible supply at the source and the demand at the
destination:
|
|
(11) |
The value 
is an implicit upper bound on the commodity
flow on the route connecting to .
An optional maximal route capacity 
may affect the feasible set and an optimal
solution only if 
.
From a practical point of view, in BTP/QDBTP and TTMTP/ QDTTMTP, parameters must
be specified explicitly, usually if the vehicle can carry the maximal payload
not larger than (e.g., due to the technical specification of
the vehicle or restrictions imposed by the condition of the road
infrastructure). Let 
denote the maximal common upper bound on the
commodity flow for all routes, which is the maximum of all the upper bounds :
|
|
(12) |
By (11) and (12):
|
|
(13) |
The inequalities (13) are
satisfied for any ,
so adding them as constraints does not affect the feasible set. After a slight
transformation, they are used to linearize .
Next,
new auxiliary binary variables are introduced:
·
– indicating if a
non-zero quantity of the commodity is transported along the route from to (
– “the route from to is used”/”one vehicle is travelling from to ” ) or
not (
– “the route from to is not used”/”zero vehicles are travelling
from to ”). .
Let
us notice that (1) can be expressed as:
|
|
(14) |
By the definition of 
,
(14) can be expressed as:
|
|
(15) |
The
following inequalities define the relationships between and which
provide an indication of whether a non-zero amount of commodity is transported
(
)
or no commodity (
)
is transported:
|
|
(16) |
Inequalities
(16) will become another group of constraints of the models, added to (5-8).
Obviously, if 
,
then (16) is equivalent to (13) and it does not affect the feasible set. If 
,
then also 
,
what, together with 
(7) results in .
The
transformation (15) is sufficient to linearize QDTTMTP by replacing (1) with
(15) in (3). However, this is not the case for QDBTP as another transformation
of the optimization model must be done because of the presence of the max
function.
The objective function of QDBTP (9) can be expressed now in the form:
|
|
(17) |
In
order to “remove” the max function from (17), a new variable 
is defined:
|
|
(18) |
Since
|
|
(19) |
then by (18) and (19):
|
|
(20) |
If
(20) is added as another
group of constraints to (5-8) and (16), then minimizing a new objective
function composed of a single variable is equivalent to minimizing the original
objective function of QDBTP (3). The variable and constraints (20) are obviously redundant
in QDTTMTP.
Finally,
the linearized versions of QDBTP and QDTTMTP are:
|
|
(21) |
|
|
|
|
|
|
|
(QDTTMTP) |
(22) |
The subject to the constraints (common for QDBTP
and QDTTMTP, unless specified):
|
|
(23) |
|
|
|
|
|
(24) |
|
|
|
|
|
(25) |
|
|
|
|
|
(26) |
|
|
|
|
|
(27) |
|
|
|
|
|
(28) |
|
|
|
|
|
(29) |
|
|
|
|
|
(30) |
In order to provide consistent numbering for linear
versions of QDBTP and QDTTMTP, some numbers of the formulas are repeated,
where (23-26) are identical to (5-8), (28) to (16) and (29) to (20)
respectively.
Obviously, if all the 
,
then QDBTP and QDTTMTP – both as nonlinear and linear optimization models –
reduce to BTP and TTMTP, respectively.
The
linear formulation of BTP (21), (23-29) is almost identical to CBTP Model II in [33].
The only difference is the lack of the budget (the maximal transportation cost)
constraint, present in [33].
On the other hand, QDBTP in its linear version can be considered as an
extension of CBTP Model II from [33]
which includes the quantity-dependent time delivery time, and with the budget
constraint being removed.
Introducing
the constraints (30) needs some more explanation. As it has been stated, if 
and, if defined, in
BTP or TTMTP are all integer, then the basic feasible solutions, and what
follows, also optimal solutions are integer. This property also holds for
QDTTMTP which is mathematically equivalent to FCTP, where the fixed cost
parameters are replaced with the time-parameters and the variable cost parameters are replaced
with the time-parameters .
Then, by [42],
the existence of integer optimal solutions is “guaranteed” in QDTTMTP like in
TTMTP. However, unlike in case of BTP, in QDBTP integer constraints on must be imposed, if necessary. Solutions of
example problems later in this paper showed that without imposing integer constraints on the
variables integer optimal values of in QDBTP are not “guaranteed” even if the
parameters if and, if defined, are all integers.
Before
introducing further theoretical considerations and presenting the results of
calculations for example problems, an important remark on the variables must be
made. The variables are
auxiliary binary variables that are defined as indicators of a non-zero ()
or zero () flow of the commodity from source to destination
. However, because of properties resulting from
(28), the interpretation of the value as an indicator of a non-zero flow from source
to destination is to some
extent ambiguous. Namely, if ,
then what means that the value indicates zero flow of the commodity from to ,
but not necessarily each zero flows must be “marked” by .
If ,
then, by (28), there can be either or what means that the value indicates all the non-zero flows of the
commodity, but it may also indicate zero flows on some routes. This ambiguity concerning the interpretation
of does
not affect finding an optimal solution – neither of QDBTP nor of QDTTMTP –
understood as all the values 
for which the objective function is minimized.
However, in QDBTP it
is possible that for some optimal values ,
the corresponding optimal values .
It is necessary to know the above fact in order to understand correctly the
results of the calculations. On the other hand, a couple of values and can never happen in an optimal solution of
QDTTMTP (it is possible only in the case of nonoptimal feasible solutions).
In real-world applications, BTP/QDBTP and
TTMTP/QDTTMTP do not need to be balanced problems. If the total maximal
possible supply of sources is not equal to the total demand of destinations,
i.e., (4) does not hold, or even more sophisticated so-called mixed constraints
occur, then (5) or (6) must be replaced with appropriate sets of constraints.
3. RESULTS
A linear programming formulation
of QDBTP was verified by addressing the problems known
from the literature of the subject, namely from [35]
and [36].
The problem considered in [36]
concerns some extension of QDBTP with the opportunity of using multiple
vehicles per route, and this is why it was not fully suitable for comparative
calculations, as the models with one vehicle per route only are considered in
this paper. Both [35]
and [36]
consider the unloading time only as the quantity-dependent component of the
delivery time. However, since the definition of QDBTP joins together all the delays added to the
“standard” transportation time on any route as the quantity-dependent time, the
abovementioned examples are obviously instances of QDBTP. Below there are more
precise characteristics of the examples and the solutions obtained in the
quoted papers compared to the solutions calculated for this paper. All the
solutions calculated for this paper were obtained by using linear programming
with binary variables 
and,
when necessary, integer constraints imposed on variables .
Detailed references to the formulas for each model are given below the tables
with the results (also for quoted results of nonlinear calculations) [44].
As
to the optimization software, Excel 365 Version 2406 and the add-in OpenSolver 2.9.4 [43]
running on Windows 11 PRO 23H2 were used. The computer was a Dell Latitude 5440
with a 13th Gen Intel Core i5-1345U 1.60 GHz processor, 16 GB of RAM, and NVMe SN740 WD 1 TB SSD.
Whereas a commonly used symbolic notation for optimal
solutions of optimization problems is to use the symbols of the variables with
the asterisk in the superscript, in this section the meaning of this notation
will be widened. The symbols 
and 
will stand for a solution calculated by the optimization software, no matter
whether it is optimal or suboptimal.
Analogically, in this section 
stands for the
minimal delivery time calculated by the optimization software. This time may be
either optimal or suboptimal.
Whereas the problems both from [35]
and [36]
were solved, the results for the problem from [36]
only are presented below. The reason is
that the problem from [35]
turned out to have the same delivery time when solved as a linear programming
problem. Instead, in the case of the problem from [36]
using linear optimization resulted in a significant improvement of the
solution.
Example
Problem
from [36]:
9 sources, 16 destinations,
unbalanced (total possible supply 171, total demand 158), non-zero unloading time at each destination, and an
integer-valued optimal solution required. The problem is
based on real-world data where sources and destinations
are located in 25 cities in Poland. The input data – parameters of the
problem are presented in Table 1.
Tab. 1
Parameters
of the example problem
|
|
Transportation times |
|
|||||||||||||||
|
Source/ |
D1 |
D2 |
D3 |
D4 |
D5 |
D6 |
D7 |
D8 |
D9 |
D10 |
D11 |
D12 |
D13 |
D14 |
D15 |
D16 |
Supplies
|
|
S1 |
2 |
6 |
5 |
6 |
6 |
8 |
9 |
14 |
11 |
9 |
12 |
14 |
10 |
11 |
13 |
15 |
15 |
|
S2 |
4 |
2 |
7 |
5 |
3 |
8 |
5 |
9 |
8 |
7 |
10 |
11 |
11 |
11 |
12 |
13 |
20 |
|
S3 |
7 |
1 |
8 |
5 |
3 |
8 |
2 |
6 |
5 |
6 |
8 |
8 |
10 |
9 |
10 |
10 |
23 |
|
S4 |
6 |
3 |
5 |
3 |
1 |
5 |
3 |
6 |
4 |
3 |
6 |
7 |
6 |
6 |
7 |
8 |
16 |
|
S5 |
7 |
6 |
5 |
2 |
3 |
2 |
6 |
8 |
4 |
2 |
4 |
7 |
3 |
4 |
5 |
8 |
21 |
|
S6 |
11 |
7 |
9 |
7 |
6 |
8 |
5 |
3 |
2 |
4 |
4 |
2 |
7 |
7 |
6 |
5 |
17 |
|
S7 |
6 |
10 |
2 |
3 |
5 |
1 |
10 |
11 |
7 |
5 |
7 |
9 |
3 |
4 |
6 |
8 |
19 |
|
S8 |
14 |
11 |
12 |
9 |
9 |
10 |
8 |
5 |
4 |
6 |
4 |
1 |
9 |
7 |
6 |
3 |
22 |
|
S9 |
13 |
10 |
9 |
9 |
8 |
6 |
9 |
8 |
5 |
6 |
2 |
4 |
5 |
3 |
2 |
2 |
18 |
|
Demands |
12 |
9 |
7 |
15 |
9 |
10 |
12 |
10 |
18 |
9 |
6 |
12 |
6 |
6 |
8 |
9 |
|
|
Unloading times |
0.33 |
0.33 |
0.17 |
0.5 |
0.33 |
0.33 |
0.33 |
0.33 |
0.67 |
0.33 |
0.17 |
0.5 |
0.17 |
0.17 |
0.33 |
0.33 |
|
Source: [36]
The
calculations in [36]
were performed for the model with the objective function (9) (transformed)
subject to (5) (with = replaced with ≤), (6-7) and (30) in three variants (two of them including additional
constraints (8)). The purpose of introducing additional constraints was to
“shrink” the feasible set and, in this way, improve the result of
calculations. Those additional constraints had nothing to do with considering
any actual restrictions of the flow of commodities and were in fact just a
“mathematical trick” serving as attempts to improve suboptimal solutions.
·
Variant 1 – the problem as described above
without additional constraints (8).
·
Variant 2 – the problem like in Variant 1 in which additional
constraints (8), as described below, were added. Moreover, a new upper bound 
,
lower than the lowest – “natural” common upper bound 
defined in (12), is imposed on the amount of
the commodity transported on each route .
This upper bound 
– the average of the solution of Variant I,
i.e., the average of 
calculated in MATLAB and in Excel. The
additional constraints (8) were 
.
·
Variant 3 – like Variant 2 but the upper bound
imposed on variables is decreased to the largest less than the upper bound in Variant 2 (
).
Calculations
whose results are presented in this paper were performed for the model (21)
subject to (23) (with = replaced with ≤), (24-25), (27-30), (a linear QDBTP). A comparison between
the results from [36]
and the ones calculated for this paper is presented in Table 2.
The
parameters are unloading times only, so 
for each
and there is
no need to repeat them in many rows. Unloading times other than 0.5 stand for rounded
values of fractions: 0.17 for 1/6, 0.333 for 1/3 and 0.67 for 2/3
what correspond for 10, 20 and 40 minutes, respectively.
Tab.
2
A brief comparison of the results for Example 2
|
|
Solution in [36] – |
Solution
calculated for this paper – linear problem |
|
|
Software |
Excel (unknown version) with built-in Solver |
MATLAB (unknown version) |
Excel 365 with add-in OpenSolver
2.9.4 |
|
Calculated minimal |
Variant 1:13.3 |
Variant 1: 12.72 |
6.333 |
|
Variant 2: 9.3 |
Variant 2: 12.34 |
||
|
Variant 3: 9.0 |
Variant 3: 13.98 |
||
|
Number of used |
Variant 1: 80 |
Variant 1: 24 |
33 |
|
Variant 2: 61 |
Variant 2: NA |
||
|
Variant 3: 62 |
Variant 3: NA |
||
|
Total
delivery |
Variant 1: 492 |
Variant 1: 176 |
179 |
|
Variant 2: 381 |
Variant 2: NA |
||
|
Variant 3: 384 |
Variant 3: NA |
||
Since Variants 2 and 3 impose upper limits on the
quantity of the commodity for each route, then the solutions for the nonlinear
model are only fully comparable to the linear model for of Variant 1. Whereas
the values returned by
optimization software theoretically should be equal for the nonlinear model in
Variant 1 and the linear model, in fact they were over twice as bad for
nonlinear optimization. The above results show that nonlinear optimization can
be an inefficient way of solving QDBTP, at least for some of its instances.
Calculations in Excel resulted in significant improvements of the value when additional
upper limits on were added (Variant 2 vs Variant 1: better by 4
hours/30.08%, Variant 3 vs Variant 1: better by 4.3
hours/32.33%). However, those results are still much worse that 
obtained for
the linear model. Calculations in MATLAB showed that additional upper limits on
improved the result slightly (Variant 2 vs Variant 1: better by 0.38
hours/2.99%) or even made it worse (Variant 3 vs Variant 1: worse by 1.26
hours/9.91%). Anyway, it is worth noting that the solution for
Variant 1 calculated in MATLAB results in lower values for the number of used
vehicles/routes and the total delivery time in comparison with any other
solution calculated in Excel, no matter if the model was nonlinear or linear.
Dropping
the integer constraints imposed on results in a solution with 
in which
the variables are
partially non-integer. The above fact proves the necessity of using integer
constraints on in QDBTP.
The
data from Table 1 was also used for an instance of the QDTTMTP problem. The
minimal total delivery time on all the routes turned out to be 101 hours, the
number of used vehicles/ routes was 17 and all the deliveries were completed
after 12.3333 hours, which is the time of delivering 11 units of the commodity
from source 3 to destination 9.
4. DISCUSSION
This
paper summarizes the concept of considering delays depending proportionally on
the quantity of the transported commodity in time minimization transportation
planning. This summary includes extending the existing interpretation of the
time-quantity dependence, naming the optimization problems, determining
connections with analogical models, and providing an efficient way of
calculating the optimal solutions [46].
The
main goals of the paper are discussed below.
The
first goal was to just formulate extensions of BTP and TTMTP to the case in
which the quantity of the commodity causes the increase of the overall delivery
time because of loading and unloading the commodity as well as slowing down the
trip. Those extensions were named the Quantity Dependent Bottleneck
Transportation Problem (QDBTP) and the Quantity Dependent Total Time
Minimization Transportation Problem (QDTTMTP), respectively. Whereas QDBTP is
not a new extension in the mathematical sense, the possible interpretation of
the quantity-time dependence was widened to compare with that presented in the
literature. Newly introduced QDTTMTP turned out to be a “time optimization
version” of the Fixed Charge Transportation Problem (FCTP).
The
second goal was to express QDBTP and QDTTMTP as linear programming problems,
based on analogical formulations for BTP and QDBTP. Those formulations
bring many advantages.
1.
They allow one to find an optimal solution in
cases when solving an original nonlinear problem – because of limitations of optimization software –
may not.
2.
It allows for using general-purpose optimization
software for solving, i.e., there is no necessity to create dedicated solving
algorithms.
It
is necessary to say that the linear formulation of QDBTP (and, to some extent,
also of QDTTMTP) results also in some issues that may be perceived negatively.
However, the issues are more technical features than real disadvantages. The issues are as follows:
1.
In the linear formulation of QDBTP or QDTTMT for
each variable standing for the quantity of the transported
commodity, an auxiliary binary variable is introduced. It means that
twice as many variables are required to compare with the linear formulation.
Moreover, the number of linear constraints to compare with the nonlinear formulation increases by 
for QDTTMTP and by 2 for QDBTP.
2.
In case of QDBTP, on some routes there may be optimal values 
“coupled” with 
.
This phenomenon means that some routes are incorrectly marked as “used”, but it
does not affect the optimality of the solution in variables. The only practical consequence is
that the total number of used routes/vehicles must be calculated as the number
of for which 
, (
)
not the number of 
for which .
The
third goal was to discuss the existence of the “guaranteed” integer optimal
solutions in the optimization models under consideration. It turned out that,
unlike in case of BTP, QDBTP does not have “guaranteed” integer optimal
solutions (in variables) even if all the maximal supplies of
sources and the demands of
destinations are integer. Technically speaking, it means that whenever the
amount of the commodity on each route must be an integer, imposing the integer
constraints on variables is necessary. This feature may be a
disadvantage only in cases when the abovementioned integer constraints are the
reason to slow down the calculations unacceptably.
5. CONCLUSIONS
In
this paper, it was shown that QDBTP formulated as a linear programming problem
can be an efficient approach to time-critical transportation planning. The most
important advantage is that this approach results in obtaining optimal
solutions in cases in which solving original nonlinear problems failed.
Moreover, problems of that kind can be solved optimally using general purpose
optimization software without the necessity of creating dedicated algorithms
and software that implement them. The abovementioned fact does not exclude,
however, searching for dedicated algorithms if using standard linear
programming turns out to result in an unacceptably long time to solve the
problems essential for real-world applications. The linear formulation of QDBTP
also allows for easily formulating problems with second-level optimality
criteria regarding many possible economic and ecological aspects of
transportation planning.
QDTTMTP
- an extension of TTMTP with an analogical quantity-dependent component of the
objective function as well as its linear formulation was also introduced in the
study.
A
possible occurrence of multiple optimal solutions in QDBTP makes it possible to
consider second-level
optimality criteria for QDBTP. Namely, for a given
(the minimal
delivery time – the optimal value of the
objective function of QDBTP) there can be alternative solutions which differ in features such as like the
total delivery time, number of used vehicles/routes, delivery cost, fuel
consumption, mileage. Each of those features (as well as possibly some other)
can become a second-level
optimality criterion, and a new optimization problem can be formulated. Such a
problem is of the form “minimize a second-level
optimality criterion (e.g., the total delivery cost) subject to the constraints
of the initial problem completed the delivery time set to . Whereas the idea of second-level optimality criteria for
QDBTP is quite simple, it requires a separate paper to be presented precisely.
Both
QDBTP and QDTTMTP can obviously be developed further in many aspects. Some
propositions are mentioned below. The two models can easily be extended to
include issues of packing and storage of the transported commodity or the
possibility of using multiple vehicles on a single route.
New
issues may arise if we consider using electric-powered vehicles (EV). Time
minimization in transportation planning assumes implicitly travelling with the
maximal speed and acceleration allowed by the traffic law and technical-safety
requirements. However, the speed and, especially, acceleration strongly affect
consumption of energy stored in batteries of the vehicles [44].
Moreover, the amount of energy required to accelerate the vehicle increases
with the mass of the transported cargo. Even if we take into account energy
recuperation during braking, there is still a possibility that at some weight
of the carried cargo, a “breaking point” can be attained at which an extra
recharging of the batteries during the trip is necessary. Because recharging
the batteries in EVs usually takes much longer compared with refueling the comparable internal combustion vehicles, the
total delivery time may increase dramatically. The above considerations show
that there is a need to develop QDBTP and QDTTMTP versions for EVs. They must
reflect the fact that, when the weight of the cargo exceeds some level, then
there is a necessity of changing the driving style to a slower, but more
energy-saving one, or, if it is impossible to avoid, to add the recharging time
to the total trip time.
Finally,
reliable modeling the delivery plans may not be
restricted to deterministic cases only. It may also require taking into account
various aspects of possible uncertainty. For example, an important factor can
be the random availability of the real-world fleets of vehicles. A promising
approach seems to be using the readiness of each vehicle described by
semi-Markov reliability models [45].
A draft idea is to combine the parameters of the deterministic QDBTP and
QDTTMTP models with parameters of the models in [45]
in order to obtain tighter, readiness-constrained capacity bounds. The above
idea is intended to be the base for a possible further development of
non-deterministic extensions of the time-minimizing delivery models.
At the same time, the study
presents certain limitations as follows.
· While the paper highlights the advantage of
formulating QDBTP as a linear programming problem (LP) to overcome the
challenges of the original nonlinear formulation, it also explicitly
acknowledges a crucial limitation: the potential for unacceptably long
addressing times when employing general-purpose LP solvers for problems of a
scale relevant to real-world applications. Linear programming can still face
significant computational burdens with a large number of variables and
constraints. Real-world transportation problems often involve numerous origins,
destinations, commodities, vehicle capacities, and time windows. The linear
formulation of QDBTP, while enabling optimality guarantees, might generate a
problem instance with a size that overwhelms standard LP solvers, leading to
impractical solution times for time-sensitive planning scenarios. This
limitation suggests that the practical applicability of the proposed LP
formulation might be restricted to smaller-scale problems or might necessitate
the use of highly optimized commercial LP solvers.
· The research conducted introduces the valuable
concept of leveraging the potential for multiple optimal solutions in QDBTP to
optimize based on secondary criteria once the minimal delivery time is
achieved. However, this remains a conceptual introduction without a concrete
formulation or detailed analysis. The paper states that "the idea of
second-level optimality criteria for QDBTP is quite simple; it requires a
separate paper to be presented precisely." This clearly indicates that the
actual mathematical formulation of how to incorporate and optimize these
secondary objectives within the constraints of the primary (minimal delivery
time) problem is not developed within the current study. Questions remain about
how to effectively model these criteria, how to handle potential trade-offs
between different secondary objectives, and the computational implications of
addressing such second-level optimization problems. This limitation entails
that the paper does not provide the methodological framework or computational
validation for implementing these second-level optimizations.
References
1.
Tolstoi A. N. 1930. „Metody nakhozhdenyianaimenshego summovogo kilometrazha pri planirovanii perevosok b prostranstve”. Planirovanie Perevozok
1: 23-55. [In Russian: “Methods
of finding the minimum total kilometrage in cargo transportation planning in
space”. Transportation Planning]. Russia,
Moscow: TransPress of the National Commissariat of
Transportation.
2.
Kantorovich Leonid Vitalyevich. 1940. „A new
method of solving some classes of extremal problems”. Doklady Akademii Nauk SSSR 28: 211-214.
3.
Hitchcock Frank Lauren. 1940. „The Distribution
of a Product from Several Sources to Numerous Localities”. Journal of
Mathematics and Physics 20: 224-230. ISSN:
1467-9590. DOI: 10.1002/sapm1941201224.
5.
Charnes Abraham, William W. Cooper. 1954. „The
Stepping Stone Method of Explaining Linear Programming Calculations in
Transportation Problems”. Management Science 1(1): 49-69.
ISSN: 0025-1909. DOI: 10.1287/mnsc.1.1.49.
7.
Dantzig George B. 1963. Linear Programming
and Extensions. New Jersey, Princeton: Princeton University Press.
8.
Shih Wei. 2007. „Modified Stepping-Stone method
as a teaching aid for capacitated transportation problems”. Decision
Sciences 18(4): 662-676. ISSN: 0011-7315. DOI:
10.1111/j.1540-5915.1987.tb01553.x.
9.
Babu Md. Ashraful, Md. Abu Helal, Mohammad
Sazzad Hasan, Utpal Kanti Das. 2013. „Lowest Allocation Method (LAM): A New
Approach to Obtain Feasible Solution of Transportation Model”. International Journal of Scientific & Engineering Research 4(11): 1344-1348. ISSN: 2347-3878.
10.
Shimshak Daniel G., James Alan Kaslik, Thomas
Barclay. 1981. „A Modification of Vogel’s Approximation Method through the Use
of Heuristic”. Information System and Operational Research (INFOR) 19:
259-263. DOI: 10.1080/03155986.1981.11731827.
11. Balakrishnan
Nagraj. 1990. „Modified Vogel’s Approximation Method for Unbalanced
Transportation Problem”. Applied Mathematics Letters 3(2): 9-11.
ISSN: 0893-9659. DOI: 10.1016/0893-9659(90)90003-T.
12. Alkubaisi Muwafaq. 2015. „Modified Vogel Method to Find Initial
Basic Feasible Solution (IBFS) – Introducing a New Methodology to Find Best
IBFS”. Business and Management Research 4(2): 22-36.
ISSN: 1927-6001. DOI: 10.5430/bmr.v4n2p22.
13. Soomro
Abdul Sattar, Muhammad Junaid, Gurudeo Anand Tularam.
2015. „Modified Vogel’s Approximation Method for Solving Transportation
Problems”. Mathematical
Theory and Modeling 5(4): 32-42. ISSN:
2224-5804.
14. Alam
Teg, Rupesh Rastogi. 2011. „Transportation Problem: Extensions and Methods: An Overview”.
VSRD-International Journal of Business & Management Research 1(2): 121-126.
ISSN: 2319-2194.
15. Barsov A.S. 1959. What is Linear
Programming? In 1964 from the 1st Russian ed. (1959) by Michael B.P. Slater,
Daniel A. Levine. Prepared by the Survey of Recent East European Mathematical
Literature. Boston,
Heath.
16.
Nesterov Evgenii Pavlovich.
1962. Transportnaya zadacha
lineynogo programmirovaniya.
Tranzheldorizdat, Moscow. P. 59-65. [In
Russian: “Transportation Problems in Linear Programming”].
17. Grabowski
Wiesław. 1964. „Problem of transportation in minimum time”. Bulletin L'Académie Polonaise des Science, Série des
Sciences Mathématiques, Astronomiques
et Physiques (BAPMAM) 12:
107-108. ISSN:
0001-4117.
18. Grabowski
Wiesław.
1964. „Transportation problems with minimal time”. Przegląd Statystyczny 11: 3-33.
19.
Szwarc Włodzimierz. 1966. „The Time
Transportation Problem”. Zastosowania Matematyki 8: 231-242.
20. Szwarc
Włodzimierz. 1971. „Some Remarks on the Time Transportation Problem”. Naval
Research Logistics Quarterly 18(4):
473-485. ISSN: 0894-069X. DOI: 10.1002/nav.3800180405.
21. Hammer Peter L. 1969. „Time-minimizing
transportation problems”. Naval
Research Logistics Quarterly 16(3):
345-357. ISSN:
0894-069X. DOI: 10.1002/nav.3800160307.
22.
Garfinkel Robert S., M.
Ramesh. Rao 1971. „The
bottleneck transportation problem”. Naval
Research Logistics Quarterly 18(4):
465-472. ISSN:
0894-069X. DOI: 10.1002/nav.3800180404.
23.
Sharma Jai Kishan, Kanti Swarup. 1977. „Time
minimizing transportation problem”. Proceedings of the Indian Academy of
Sciences – Section A (Mathematical Sciences) 86: 513-518. ISSN:
0973-7685. DOI: 10.1007/BF03046907.
24. Bhatia
Harish Lal, Kanti Swarup, M.C. Puri. 1977. „A procedure for time minimization
transportation problem”. Indian Journal of Pure and Applied Mathematics 8(8): 920-929. ISSN: 0019-5588.
25.
Seshan Chidambaram Ramachandran, Vishwanath
Gajanan Tikekar. 1980. „On Sharma-Swarup algorithm for time minimizing
transportation problems”. Proceedings of the Indian
Academy of Sciences – Section A (Mathematical Sciences) 89: 101-102. ISSN: 0973-7685. DOI:
10.1007/BF02837265.
26. Issermann Heinz. 1984. „Linear bottleneck
transportation problem”. Asia Pacific Journal of Operational
Research 1: 38-52. ISSN: 0217-5959.
27. Frieze
Anthony M. 1975. „Bottleneck linear programming”. Journal of the Operational
Research Society 26(4):
871-874. ISSN: 0160-5682. DOI: 10.1057/jors.1975.179.
28. Dearing
Perino M., F.C. Newruck 1979. „A Capacitated Bottleneck
Facility Location Problem”. Management Science 25(11): 1093-1104.
ISSN: 0025-1909. DOI: 10.1287/mnsc.25.11.1093.
30. Agarwal
Swati, Shambhu Sharma. 2018. „A Minimax Method for Transportation Problem with
Mixed Constraints”. International
Journal of Computer & Mathematical Sciences 7(3): 1-6. ISSN: 2347-8527.
32. Xie
Fanrong, Yuchen Jia, Renan Jia. 2012. „Duration and cost optimization for
transportation problem”. International Journal on Advances in Information
Sciences and Service Sciences 4(6): 219-233. ISSN: 1976-3700. DOI:
10.4156/AISS.vol4.issue6.26.
33.
Charnsethikul Peerayuth,
Saeree Svetasreni. 2007. „The Constrained Bottleneck
Transportation Problem”. Journal of Mathematics and Statistics 3(1):
24-27. ISSN: 1549-3644. DOI: 10.3844/jmssp.2007.24.27.
34.
Achary K.K., C.R. Seshan 1981. „A time
minimising transportation problem with quantity dependent time”. European Journal of
Operational Research 7(3):
290-298. ISSN: 0377-2217. DOI: 10.1016/0377-2217(81)90187-7.
35. Małachowski Jerzy, Józef Żurek,
Jarosław Ziółkowski, Aleksandra Lęgas. 2019. „Application of the
Transport Problem from the Criterion of Time to Optimize Supply Network with
Products „Fast-Running””. Journal of KONBiN 49(4): 127-137. ISSN: 1895-8281. DOI: 10.2478/jok-2019-0079.
36. Ziółkowski Jarosław, Aleksandra Lęgas, Elżbieta Szymczyk, Jerzy
Małachowski, Mateusz Oszczypała, Joanna Szkutnik-Rogoż. 2022.
„Optimization of the Delivery Time within the Distribution Network Taking into
Account Fuel Consumption and the Level of Carbon Dioxide Emissions into the
Atmosphere”. Energies
15(14): 5198. ISSN: 1996-1073. DOI:
10.3390/en15145198.
37. Nechitaylo Nikolay Mikhailovich. 2021. „A Type of Transportation
Problem to be Solved Following the Time Criterion and Considering Vehicle
Features”. World of Transport and Transportation 19(3): 74-80. ISSN: 1992-3252. DOI:
10.30932/1992-3252-2021-19-3-8.
38.
Nikolić Ilija. 2007. „Total time minimizing
transportation problem”. Yugoslav Journal
of Operations Research 17(1): 125-133. ISSN: 0354-0243. DOI:
10.2298/YJOR0701125N.
39. Bansal
S., M. C. Puri 1980. „A min-max problem”. Zeitschrift
für Operations Research 24: 191-200. ISSN: 0340-9422. DOI:
10.1007/BF01919246.
40.
Fisk John, Patrick G. McKeown. 1979. „The pure
fixed charge transportation problem. Naval Research Logistics Quarterly 26(4): 631-641.
ISSN: 0894-069X. DOI: 10.1002/nav.3800260408.
41.
Zhu Pengfei, Guangting Chen, Yong Chen, An Zhang. 2025.
„On the pure fixed charge transportation problem”. Discrete Optimization
55(C): 100875. ISSN: 1572-5286. DOI: 10.1016/j.disopt.2024.100875.
42. Hirsch
Warren M., George B. Dantzig. 1968. „The fixed charge problem”. Naval
Research Logistics Quarterly 15(3): 413-424. ISSN: 0894-069X. DOI:
10.1002/nav.3800150306.
43.
Mason Andrew J. 2012. „OpenSolver – An Open Source Add-in to Solve
Linear and Integer Progammes in Excel”. Operations
Research Proceedings 2011: 401-406. Springer: Berlin/Heidelberg, Germany.
ISBN: 978-3-642-29209-5. DOI: 10.1007/978-3-642-29210-1_64.
44. Kozłowski Edward, Piotr Wiśniowski,
Maciej Gis, Magdalena Zimakowska-Laskowska, Anna Borucka. 2024.
„Vehicle Acceleration and Speed as Factors Determining Energy Consumption in
Electric Vehicles”. Energies 17(16): 4051. ISSN: 1996-1073. DOI: 10.3390/en17164051.
45. Kozłowski Edward, Anna Borucka, Piotr
Oleszczuk, Norbert Leszczyński. 2024.
„Evaluation of Readiness of the Technical System Using the Semi-Markov Model
with Selected Sojourn Time Distributions”. Eksploatacja i Niezawodność – Maintenance
and Reliability 26(4). ISSN: 1507-2711. DOI:
10.17531/ein/191545.
46.
Justiani
Sally, Budhi S. Wibowo. 2022. „The Economic and
Environmental Benefits of Collaborative Pick-Up in Urban Delivery Systems”. LOGI
– Scientific Journal on Transport and Logistics 13(1): 245-256. ISSN:
2336-3037. DOI: 10.2478/logi-2022-0022.
Received 15.05.2025; accepted in revised form 09.08.2025
Scientific Journal of Silesian
University of Technology. Series Transport is licensed under a Creative
Commons Attribution 4.0 International License