Article citation information:
Nabadova, G. Controlling
the movement of hexacopter along the intended route with engine failure. Scientific Journal of Silesian University of
Technology. Series Transport. 2025, 126,
149-160. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2025.126.9.
Gulush NABADOVA[1]
CONTROLLING THE MOVEMENT OF HEXACOPTER ALONG THE INTENDED ROUTE
WITH ENGINE FAILURE
Summary. This article
investigates the issue of controlling the movement of a hexacopter-type
unmanned aerial vehicle around a route. The movement of the hexacopter is
modeled as the motion of a rigid body, taking into account gravitational forces
and aerodynamic resistance forces. The spatial orientation of the hexacopter is
expressed using quaternions. The movement route is considered as a broken line
consisting of straight-line segments, and parameters that control the
hexacopter's flight on the considered straight-line segment of the route are
determined when one of its engines fails. The mathematical rationale for how to
control the operational engines to continue the hexacopter's movement as before
in the event of an engine failure is provided.
Keywords: hexacopter,
route, control parameters, engine failure, quaternion, spatial orientation,
unmanned aerial vehicle
1.
INTRODUCTION
Recently, with the widespread application of
multi-engine drones, various types have become particularly popular depending
on their purpose and the demands placed upon them [1, 2, 3]. Unlike single-engine drones, the failure
of engines in multi-rotor devices can lead to safety-related issues. Numerous
published articles suggest solving this problem by redesigning the control law
or control power [4, 5]. However, this approach is challenging to implement
because altering the control power in this manner usually requires the addition
of extra devices.
Several studies have been conducted on the
detection of engine failure, maneuverability of unmanned aerial vehicles (UAVs)
with engine failure, and the distribution of control among engines [6-8]. Rapid
detection of an engine failure in a UAV is crucial for subsequent actions. A
novel method for fault diagnosis using thermal imaging was presented in [9]. Lu
[10] proposed a Fault Detection and Isolation (FDI) system capable of instantly
detecting and isolating a failed engine in quadcopters with a completely failed
engine. Merheb [11] suggested a search table to convert a quadcopter into a
tri-rotor in the event of a complete failure of one rotor. Nagarjuna and Suresh
developed a safe landing sequence [12]. Lee and colleagues used two servo
motors to control the relative roll and pitch attitudes of a quadcopter to
maintain its stability when a motor failure is detected [13]. Wang and Zhang restructured
control commands using a sliding mode control algorithm [14].
Regarding the above-mentioned studies, several
questions remain unanswered: first, most previous research has only considered
quadcopters with a single engine failure. Secondly, there is not enough
material on how to control a hexacopter using quaternion theory methods in such
situations.
In this article, the issue of controlling a
hexacopter when one of its engines fails under power constraints is examined.
The proposed system can assist in the control design when there is an engine
failure and increase the likelihood of a successful emergency landing.
For clarity, the engines of the hexacopter will
be numbered in the sequence shown in Figure 1. The rotational directions of the
engine propellers are schematically presented in the same figure.
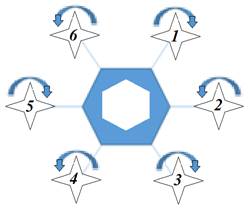
Fig. 1. Rotation direction of the hexacopter’s
propellers
In scientific and technical literature, various
simulation models of hexacopter movement can be found. Depending on the
characteristics of the sensors used in solving the feedback automatic control
problem, the flight models of hexacopters differ from one another. During the
research, the use of MPU6050 sensors in the studied UAV made it more
appropriate to use quaternions as orientation parameters in its mathematical
model [15]. This is because MPU6050 sensors measure the rate of change of
orientation angles rather than the angles themselves. Numerous articles by
various authors have been dedicated to the model of a UAV expressed using quaternions
[16, 17, 18, 19]. The model considered here essentially corresponds to the
model in [17].
2. PROBLEM STATEMENT
When considering the case where
there are no power limitations on the hexacopter's engines (referred to as the
normal case below), it becomes apparent that the control of a hexacopter along
a straight-line trajectory, even with one engine failure, is fundamentally
similar to the control of a quadcopter. This situation also suggests that a
hexacopter can be effectively controlled along a straight-line trajectory even
if two symmetrically positioned engines fail. The failure of one engine in a
hexacopter refers to the scenario where one of its six engines is
non-operational. In such cases, it is typically recommended to shut down the
engine symmetrically positioned with respect to the hexacopter's center. It is
evident that when the number of engines is reduced from six to four, their
power needs to be increased. However, a question arises: can the operation of
one failed engine be compensated by the remaining five engines in a hexacopter
if there are power limitations? This article investigates this issue. Below,
the mathematical formalization and solution of the problem are provided.
The mathematical model of the
hexacopter is expressed through the interaction between quantities calculated
in local and global coordinate systems. Let us introduce the coordinate systems
used, as shown in the following figure (Figure 2):
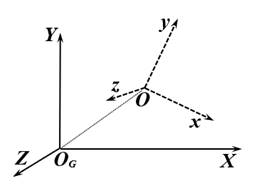
Fig. 2. The local and inertial coordinate
systems
is the inertial coordinate system associated
with the ground, while 
is the local coordinate system linked to the
hexacopter, with its origin at the hexacopter's center of gravity, used to
determine its orientation in space.
For clarity, let's assume that the origin 
of the system is fixed at a certain point on the
Earth's surface. The 
axis of the coordinate system points north, the 
axis points east, and the 
axis is directed upwards, perpendicular to
both the and axes.
Let's assume that the ox axis of the 
system is aligned along the hexacopter's first
arm, the 
axis is perpendicular to the 
axis and lies in the
plane of the hexacopter's arms, and the 
axis is aligned along the
hexacopter's symmetry axis, perpendicular to the 
plane. In the case of horizontal stillness, it
is assumed that the 
axis is directed upwards, and the system is a right-handed coordinate system.
3. ORIENTATION GIVEN BY QUATERNIONS
Brief information about quaternions is needed
to express the orientation of the UAV in this study.
The general form of a quaternion is given as 
, which is a 4-dimensional hypercomplex number [15]. Here, 
are real numbers, and 
are imaginary units.
The multidimensional nature of quaternions makes them a convenient and adequate
tool for representing rotation angles. Using quaternions allows us to represent
the spatial position of a flying vehicle as follows:
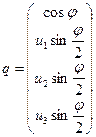(1)
Here 
is the rotation axis
vector to achieve the current rotational state of the aircraft, and 
is the principal rotation angle [20].
Specifically, if the rotation axis coincides with the 
axis, and is the principal rotation angle, then 
and:
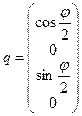(2)
Assume that the local coordinate system is rotated by a vector 
relative to the inertial
coordinate system . Then, to calculate the coordinates of a vector given in the local
coordinate system in the inertial coordinate system, the following
transformation matrix can be applied [20]:
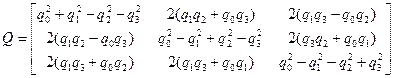(3)
It is clear that to find the coordinates of a vector given in the coordinate system relative to the coordinate system, the inverse of
the transformation matrix 
should be applied. The elements of the inverse
matrix are denoted as follows:
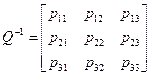. (4)
4. MATHEMATICAL MODEL OF HEXACOPTER
As
mentioned earlier, for simplicity, the mathematical model of the UAV will not
consider gravitational and aerodynamic forces.
At a given
time
, let the hexacopter's center of gravity have the coordinates
in the 
inertial coordinate
system. Also, let the orientation of the local 
coordinate system
relative to the inertial coordinate system be expressed by the
quaternion 
. Denote the angular velocity of the rotation of the 
-th rotor of the hexacopter by 
. Then, the movement of the hexacopter, i.e., the rotation of
the rotors 
and the translational
movement 
, will be described by the following equations, where the
rotation vector and the quaternion 
are interrelated. If
we denote the velocity of the hexacopter in the local coordinate system as
, then the
equations of motion expressed in quaternions for the hexacopter will be written
as follows [21]:
(5)
Here, 
is the mass of the hexacopter, 
is the drag
coefficient, 
is the acceleration
due to gravity, and 
is a vector composed
of the elements of the last column of the inverse matrix 
.
If we denote the angular velocity of the
hexacopter as 
, then, based on the total moment 
exerted on it, the
following equations can be written [19, 20]:
(6)
Here 
is the inertia matrix.
The moment
depends on the velocities 
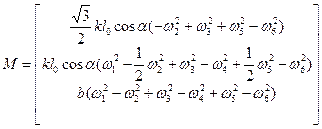as follows [17]:
. (7)
Here, 
is the distance
between the center of gravity of the hexacopter's main body and the center of
gravity of the motor located at the end of its arm (Figure 3),
is the thrust coefficient of the motor, and 
is the drag
coefficient.
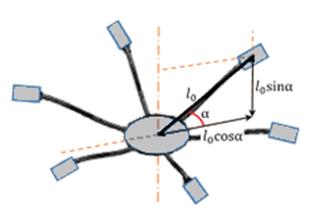
Fig. 3. Structural dimensions of the hexacopter
It
should be noted that starting from the angular velocity
found in equation (6), the current orientation quaternion
of the hexacopter can be calculated by solving the following system of ordinary
differential equations (Poisson's kinematic equations) [21]:
. (8)
5. MATHEMATICAL FORMALIZATION OF PROBLEM
As
mentioned above, for simplicity, the mathematical model of the UAV takes into
account gravitational force, aerodynamic forces, and the thrust force of the
engines. The third equation, which directly includes the rotational speeds of
the engines, can be written as follows:
. (9)
Here:
(10)
Considering
the condition that the torques generated by the hexacopter's engines are equal
to zero during its linear motion, in equation (7):
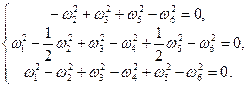(11)
Thus, in
order to provide the linear motion of the hexacopter at a certain velocity 
, the quantities must satisfy the
system of equations (9)-(11).
6. PROVIDING CONTROL IN NORMAL OPERATING MODE.
Assume
that all the engines of hexacopter are functioning normally. In this case, let
us investigate the problem of determining the quantities that satisfy the
system of equations (9)-(11).
For
every k, let us denote 
as 
. Then the system (9)-(11) can be
written as follows:
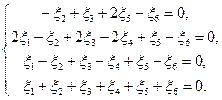(12)
As it can be seen, equation (12) is a system of linear equations
written with respect to six unknowns, and its rank is equal to four. Therefore,
this system has infinitely many distinct solutions. The following optimality
criterion can be used to select the most suitable solution from the set of
possible solutions that align with the essence of the problem:
. (13)
The minimization of the
functional essentially requires that the quantities 
, and ultimately the rotation frequencies , be as close as possible to each other. This requirement is
justified by the fact that during the control of the straight-line motion of
the UAV, its engines should be loaded as equally as possible.
Mathematically,
the problem defined by equations (12) and (13)
is a constrained optimization problem with respect to the variables . To solve this, the Lagrange multipliers method can be used
[20]. For this purpose, let us denote the expressions on the left side of the
equations (12) as 
. Then, by introducing the multipliers 
, the Lagrange function for the problem defined by equations
(12) and (13) can be written as follows:
. (14)
Thus, the constrained optimization problem defined by equations (12) and
(13) reduces to the problem of finding the unconstrained minimum of the
functional (14). To find the minimum of the 
functional, let's compute its partial
derivatives with respect to the variables 
and 
and set them equal to zero. This will result
in the following system of equations:
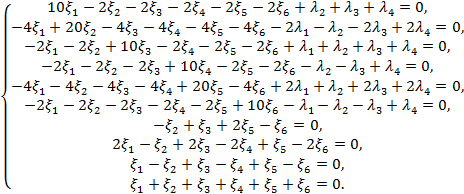(15)
If we solve this system
of equations using Cramer's rule, we will obtain the following results:
, 
. (16)
Based on the calculated values of the
quantities , we obtain the following values for the rotation frequencies
of the propellers:
. (17)
Thus, for the hexacopter to fly in a straight
line, it is first brought into the appropriate orientation and achieves the
desired pitch by adjusting the rotation frequencies of the propellers. After
that, it is controlled along the corresponding trajectory using the engines operating
at the rotation frequencies given by equation (17). (It should be noted that
the calculation of the propeller rotation frequencies required for changing the
UAV's orientation is not considered in this paper).
7. CONTROLLING THE HEXACOPTER WITH ENGINE FAILURE
As seen from (17), the optimal control of
straight-line flight when all motors are operating normally is provided by
rotating all propellers at the same frequency. Suppose one of the hexacopter's
motors has failed. Without generalizing, it can be assumed that the failed
motor is, for example, the 6th motor. In the absence of constraints on the
rotation frequencies of the motors, the issue of controlling the hexacopter's
movement has been addressed in [21], and it has been shown that control is possible
along a straight-line trajectory when 
. As mentioned above, a question arises: if the power of the
motors is insufficient, and they cannot achieve the rotation frequencies given
in (17), can the hexacopter be controlled in the previous mode using 5 motors?
The failure of the 
motor means that 
must be taken when
solving the system (9)-(11). Thus, the system (9)-(11) is transformed into a
system of four equations written with respect to five unknowns. After
substituting 
,
the analog of system (17)
is written as follows:
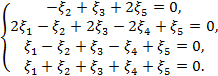(18)
To choose the most suitable solution from the
set of possible solutions according to the essence of the problem, we can take
the following optimality criterion as the analog of functional (13):
. (19)
In this
case, let's solve the problem with constraints applied to equations (18). If
the 6th engine is not working, then the problem with constraints will be as
follows:
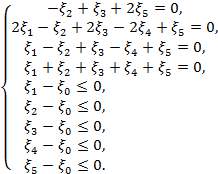(20)
This problem is mathematically a conditional
extremum problem. Various approaches can be applied to solve the problem [4].
During the research, the Kuhn-Tucker method was used [22]. If a solution to
this problem exists, then it must satisfy all the minima obtained by solving
with each of the individual additional conditions:
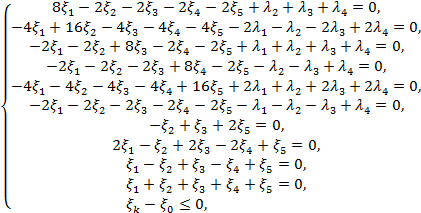(21)
.
For 
, this system of equations can be solved with each of the
corresponding constraint conditions, and it turns out that the system is
consistent. However, when the system is solved with the second constraint
condition, it becomes apparent that there is no solution to this problem. This
means that when constraints are applied to the engines, it is not possible to
compensate for the failure of one engine using the remaining five engines.
It is clear that the same result is obtained if
any of the 
, 
, or 
engines fail.
It should be noted that the terms related to
the 1st and 5th engines are not included in the 1st equation of system (18)
. This is due to the placement of these engines relative to
the 
coordinate system. For clarity, if we consider
the case where the 1st engine fails instead of the engine, by solving the
resulting system in a similar manner, we again conclude that the hexacopter
cannot be controlled with five engines under the given power constraints.
Naturally, the results are similar when the 
engine fails.
Thus, this means that under the given
constraints, it is not possible to control the hexacopter along a straight-line
trajectory using only five engines.
8. CONCLUSIONS
Thus, the research showed that when one of the
hexacopter's engines fails, the continuation of its movement along the previous
trajectory can be ensured by the other engines, except for the engine
symmetrically positioned relative to the failed one. In this case, if there are
no technical limitations on the power of the engines, it is necessary to
increase the rotation frequency of the propellers to continue the movement at
the previous speed.
However, if there are power limitations on the
engines, the continuation of the flight along the trajectory can be achieved by
reducing the movement speed. It was also mathematically substantiated that
under such limitations, the power deficiency across four engines cannot be
compensated by the fifth engine to maintain the hexacopter's flight speed along
a straight trajectory at its previous level.
References
1.
Alderete T.S. 1995. Simulator aero model implementation. NASA Ames Research Center, Moffett Field, California, 21.
2.
Bayramov A.A., A.B. Pashayev, E.N. Sabziev,
M.M. Tatur, A. Konikov. 2021. „Model of navigation and control of unmanned
ground vehicles used in agriculture”. In: Proceedings of
the 2nd International Congress on „Applied Sciences”: 217-222.
Karabagh, Azerbaijan, 8-10 November 2021.
3.
Massimo Cefalo, Josep
M. Mirats-Tur. 2011. „A comprehensive dynamic model for class-1 tensegrity
systems based on quaternions”. International
Journal of Solids
and Structures 48(5): 785-802.
4.
Aoki Yusuke, Asano Yuta, Honda Akihiko,
Motaaka Norizumi, Hoshino Kenta, Ohtsuka Toshiyuki. 2021. „Nonlinear model
predictive control for hexacopter with failed rotors based on quaternions – simulations and hardware experiments”. Mechanical
Engineering Journal 8(5): 21-00204.
5.
Wen F.H., F.Y. Hsiao, J.K. Shiau. 2021.
„Analysis and management of motor failures of hexacopter in hover”. Actuators 10(3): 48. MDPI. DOI: 10.3390/act10030048
6.
Cheon J.M., C.K. Kim, J.M. Lee, S. Kwon. 2006.
„New Method for Detecting Failures of Power Converter Module in Control Rod
Control System”. In: Proceedings
of the 2006 IEEE International Symposium on „Industrial Electronics” 2: 1566-1570.
Montreal, QC, Canada, 9-13 July 2006. IEEE. ISSN:
2163-5145.
7.
Contreras-Medina
L.M., de Jesus Romero-Troncoso R., E. Cabal-Yepez, de Jesus Rangel-Magdaleno
J., J.R. Millan-Almaraz. 2009. „FPGA-based
multiple-channel vibration analyzer for industrial applications in induction
motor failure detection”. In: Proceedings
of the IEEE Transactions on „Instrumentation and Measurement” 59(1): 63-72. ISSN:
1557-9662.
8.
Hasan A., V. Tofterup, K. Jensen. 2019. „Model-based fail-safe module
for autonomous multirotor UAVs with parachute systems”. In: 2019 International Conference on
„Unmanned Aircraft Systems (ICUAS)”: 406-412. Atlanta, GA, USA, 11-14
June 2019. IEEE. ISSN: 2575-7296.
9.
Glowacz A. 2021. „Fault diagnosis of
electric impact drills using thermal imaging”. Measurement 171(1-4):
108815. Elsevier BV. DOI: 10.1016/j.measurement.2020.108815.
10.
Lu P., E.J. van
Kampen. 2015. „Active
fault-tolerant control for quadrotors subjected to a complete rotor failure”.
In: Proceedings of the 2015 IEEE/RSJ
International Conference on „Intelligent Robots and Systems (IROS)”:
4698-4703. Hamburg, Germany, 28 September 2015. IEEE.
ISSN: 978-1-4799-9994-1.
11.
Merheb A.R., H. Noura, F. Bateman. 2014. „A novel emergency controller
for quadrotor UAVs”. In: Proceedings
of the 2014 IEEE Conference on „Control Applications (CCA)”: 747-752.
Juan Les Antibes, France, 8-10 October
2014. IEEE. ISBN: 978-1-4799-7409-2.
12.
Nagarjuna K., G.R. Suresh.
2015. „Design of effective landing mechanism for
fully autonomous Unmanned Aerial Vehicle”. In:
Proceedings
of the 2015 3rd International Conference on „Signal Processing, Communication
and Networking (ICSCN)”: 1-6, Chennai, India, 26-28 March 2015.
IEEE. ISBN: 978-1-4673-6823-0.
13.
Lee S.J., I. Jang, H.J. Kim. 2020.
„Fail-safe flight of a fully-actuated quadrotor in a single motor failure”. IEEE
Robotics and Automation Letters 5(4): 6403-6410. DOI: 10.1109/LRA.2020.3013862. ISSN: 2377-3766.
14.
Wang B., Y. Zhang.
2017.
„An adaptive fault-tolerant sliding mode control allocation scheme for
multirotor helicopter subject to simultaneous actuator faults”. IEEE
Transactions on Industrial Electronics 65(5):
4227-4236.
15.
Großekatthöfer K., Z. Yoon. 2012. „Introduction into quaternions
for spacecraft attitude representation”. Technical
University of Berlin. Berlin, Germany.
16.
Tzoumanikas D., Q. Yan,
S. Leutenegger. 2020. „Nonlinear MPC
with motor failure identification and recovery for safe and aggressive
multicopter flight”. In: Proceedings
of the 2020 IEEE International Conference on „Robotics and Automation (ICRA)”:
8538-8544. Paris, France, 31 May 2020. IEEE. DOI: 10.1109/ICRA40945.2020.9196690
ISSN 2577-087X.
17.
Artale V., C.L.R.
Milazzo, A. Ricciardello. 2013. „Mathematical
modeling of hexacopter”. Applied
mathematical sciences 7(97):
4805-4811.
18.
Alaimo A., V. Artale,
C.L.R. Milazzo, A. Ricciardello. 2014. „PID
controller applied to hexacopter flight”.
Journal
of Intelligent & Robotic Systems 73:
261-270. DOI: 10.1007/s10846-013-9947-y.
19.
Амелькин
Н.И. 2010.
„Динамика твердого
тела”.
Учебное
пособие. М.: МФТИ: 80 с. [In Russian: Amelkin N.I. 2010.
„Dynamika tverdogo tela”. Uchebnoe posobie. Moscow, MPhTI, 80 p.] ISBN:
978-5-7417-0347-2.
20.
Nisar B., M. Kamel,
R. Siegwart. 2018. „NMPC for multicopter's trajectory
tracking using modified rodrigues parameters”. In:
Proceedings
of the 2018 IEEE Conference on „Control Technology and Applications (CCTA)”: 683-689. Copenhagen, Denmark, 21-24 August 2018.
IEEE. ISBN: 978-1-5386-7698-1.
21.
Bertsekas D.P. 2014. „Constrained
optimization and Lagrange multiplier methods”. Athena Scientific. ISBN:
1-886529--04-3.
22.
Lange K. 2013.
„Karush-Kuhn-Tucker Theory”. In: Optimization. Springer Texts in
Statistics: 95. Springer, New York, NY. DOI: 10.1007/978-1-4614-5838-8_5.
Received 26.09.2024; accepted in
revised form 12.12.2024
Scientific Journal of Silesian University of Technology. Series
Transport is licensed under a Creative Commons Attribution 4.0
International License