Article citation information:
Kota, R.B., Pallela, S.S., Lalam, G. Capacity analysis at urban uncontrolled
intersections under mixed traffic conditions: a case study in Warangal city. Scientific Journal of Silesian University of
Technology. Series Transport. 2025, 126,
97-116. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2025.126.6.
Ramesh Babu KOTA[1], Sruthi Sekhar PALLELA[2], Govinda LALAM[3]
CAPACITY ANALYSIS AT URBAN UNCONTROLLED INTERSECTIONS UNDER MIXED
TRAFFIC CONDITIONS:
A CASE STUDY IN WARANGAL CITY
Summary. The
performance of the road network depends on the capacity of the intersection in
the area. Estimation of capacity becomes difficult under mixed traffic
conditions where different types of vehicles share common space without
following priority rule. Yield- controlled and stop sign-controlled
intersections operate similarly to uncontrolled intersections in India due to
lack of respect for priority rules and lane discipline. The current study
estimated capacity using critical gaps based on the HCM
methodology and examined the relationship between occupancy time and capacity.
Aiming to develop a model to estimate capacity directly from occupancy time.
Five three-legged uncontrolled intersections were selected and data were
acquired through a video camera. The occupation time and gap data were
extracted manually and the effect of various geometric and traffic parameters
like median width, conflicting flow, proportion of heavy vehicles in the
conflicting flow, and pedestrian flow on extracted occupation time using
correlation and regression analysis was studied. The results of the study
stated that with a 5% increase in conflicting flow occupation time was
increased by 0.2 sec and with a 1% increase in heavy vehicles in conflicting
flow, occupation time increased by 0.35 sec, and for a 5% increase in
pedestrian volume the occupation time of minor approach is increased by 0.13
sec. Two-wheelers and Three-wheeler vehicles had the least critical gap and the
highest was observed for heavy vehicles. Capacity was found to decrease with an
increase in occupation time. A linear regression model was developed to
estimate capacity using occupation time. This paper can provide a better
understanding of the occupation time and its effect on movement capacity.
Keywords: traffic
flow, capacity analysis, regression analysis, uncontrolled intersection, mixed
traffic condition
1.
INTRODUCTION
The overall performance of the
roadway network is heavily dependent on the capacity of the intersections. An
intersection is a shared area where two or more roads cross, making the shared
area a potential conflicting zone. According to the Highway capacity manual (HCM, 2010) capacity is defined as the maximum hourly rate
at which vehicles are expected to pass through a section or a point of a roadway
under prevailing conditions
2. LITERATURE REVIEW
2.1 Studies based on occupation time
Mohan et al. (2018) estimated the
critical gap at TWSC intersection based on occupation
time data and compared it with Modified Raff method (1950), maximum likelihood
method, and the capacity estimated from the critical gap obtained from the
occupation time method was found closer to field values
2.2 Studies based on the critical
gap
Pawar et al. (2022) demonstrated that the
accepted gaps can be used as a surrogate safety measure to estimate the crash
likelihood at unsignalized T-intersections and
validated the approach through statistical modeling and risk characterization,
showing a close approximation with actual crash data.
2.3 Studies based on capacity
Asaithambi and Aswini
(2022) estimated capacity using HCM (2010) and the
conflict flow method with high pedestrian flow. The capacity of intersections
with high pedestrian flow had 24 percent less compared to no pedestrian flow
From the literature review, it is
identified that the capacity for uncontrolled intersection is estimated by
different approaches such as gap acceptance models, empirical, conflict
techniques, and occupation time analysis. There are different procedures to
estimate critical gaps and most of them are modeled for homogenous traffic
conditions. Indian traffic conditions are far from homogenous, with varying
vehicle types, lack of lane discipline, and priority rules while crossing an
intersection area. Therefore, these methods provide an incorrect estimation of
the critical gap, which results in an incorret
capacity estimation of uncontrolled intersections. Numerous factors such as
drivers' age, approach speed, occupancy, waiting time, and conflicting vehicle
type were found to show a significant impact on driver behavior when
maneuvering in intersection areas. From the above studies, it was identified
that the clearing behavior method which uses occupation time for estimation of
critical gap suits mixed traffic conditions as it considers actual vehicle
behavior while clearing conflict areas of intersection. In the present study,
it is planned to use the concept of occupation time for estimating the capacity
of an urban uncontrolled intersection concerning prevailing traffic parameters
such as conflicting flow, percentage of heavy vehicles, and pedestrian flow.
3. DATA COLLECTION AND DATA
EXTRACTION
The data collection for this study
was conducted at five different uncontrolled T-intersections, each with three
legs. All the five intersections are located in the city Warangal. To gather
accurate information, a video camera was set up on a nearby building at each
intersection. The placement allowed the camera to capture the entire
intersection area, ensuring that all approaches and vehicle movements were
clearly visible. For each intersection, data were recorded over a period of six
hours focusing on the busy morning and evening hours when traffic was at its
peak. The data collection took place on typical weekdays to reflect regular
traffic patterns. The specific locations of the intersections studied are shown
in Figure 1.
In addition to the traffic data,
detailed geometric data about each intersection was also collected, including
the number of lanes, whether there were medians on the major and minor roads,
and the presence of features such as cycle tracks and shoulders. Precise
measurements were taken using a measuring tape and a measuring wheel to
determine the width of the lanes, the width and length of the medians, the width
of the approaches to the intersection, and the width of any shoulders that were
present. These measurements were crucial for understanding the physical layout
of each intersection and how it might influence traffic flow and safety. The
road geometric details are listed out in Table 1.
The table summarizes
that the major lanes are consistently 4-lane divided while minor lanes vary
between divided and undivided configurations. Lane widths range between 2 m and
4 m, with median widths present for major lanes but often missing for minor
lanes. This absence could impact traffic flow and safety as medians play a
critical role in controlling vehicle movement and providing refuge for
pedestrian.
|
I. Dargah intersection |
II. Erragattu intersection |
|
III. Madikonda intersection |
IV. Neelima intersection |
|
V. Hanamkonda
bus stand intersection |
|
Fig. 1. Images of
intersections identified
Tab. 1
Geometric details of the
intersections
|
Intersection |
No of lanes |
Lane width (m) |
Median width (m) |
|||
|
Major |
Minor |
Major |
Minor |
Major |
Minor |
|
|
I |
4-lane divided |
2-lane divided |
3.5 |
2.5 |
1.4 |
1.4 |
|
II |
4-lane divided |
2-lane undivided |
3.3 |
2.25 |
1.2 |
- |
|
III |
4-lane divided |
2-lane undivided |
4 |
2 |
2 |
- |
|
IV |
4-lane divided |
2-lane undivided |
3.3 |
3 |
1.1 |
- |
|
V |
4-lane divided |
2-lane undivided |
2.25 |
2 |
0.6 |
- |
4. FIELD DATA ANALYSIS
Traffic data collected at the
selected intersections were extracted manually using an MPC-HC
media player. Vehicles are categorized into two-wheelers (2W),
three-wheelers (3W), cars, buses, Heavy Commercial
Vehicles (HCV), Buses, Light Commercial Vehicles (LCV), Tractors, and Bicycles.
Classified vehicle volume count and turning movements were extracted at each
5-minute interval. The peak hour flows calculated at each intersection are
shown in Table 2.
Tab. 2
Peak hour flows
|
Intersection |
Major approach 1 |
Major approach 2 |
Minor approach |
Peak hour volume (PCU/hr) |
|||
|
TH |
RT |
TH |
LT |
RT |
LT |
||
|
I |
1568 |
105 |
1050 |
171 |
203 |
72 |
3169 |
|
II |
1094 |
256 |
887 |
101 |
84 |
298 |
2721 |
|
III |
943 |
286 |
1096 |
118 |
55 |
355 |
2836 |
|
IV |
1066 |
285 |
941 |
78 |
93 |
268 |
2731 |
|
V |
1199 |
191 |
768 |
184 |
139 |
199 |
2680 |
The vehicle composition, the
proportion of turning movements, and approach-wise volume count are represented
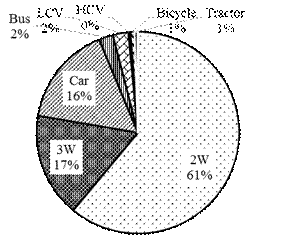
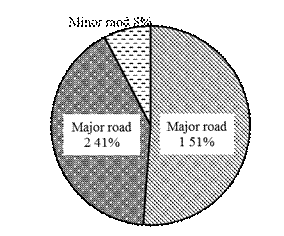
in the form of pie charts as shown in Figure 2.
|
a)
Vehicular distribution |
b)
Approach-wise distribution |
Fig. 2. Percentage of
percentage vehicular distribution and leg-wise distribution at
the intersection I
From the above pie charts, it is
evident that the proportion of two-wheelers is high. A similar trend was
observed in all the intersections, varying from 50% to 66%, which comprises
half of the total traffic in the intersections. The percentage of cars varies
from 15% to 21%, closely followed by the proportion of three-wheelers, which is
10% to 20%. LCVs vary from 2% to 6%. HCVs at the intersections vary from 1% to
7%. It can also be noticed that more than three-quarters of the traffic are
private vehicles, which implies that the private mode of transportation is
relatively preferred compared to public transportation modes such as buses or
three-wheelers. From the approach-wise distribution volume towards Major road-1
and Major road-2 of the intersections cater 45%-52% and 36%-41% and minor roads
cater 8%-16% of the traffic. The minor approach which has the least volume
among the other approaches is used to estimate the overall performance of the
intersection. Hence analysis of minor road movements
especially minor right maneuvers is chosen for the present study. It was
observed that the pedestrian crossings are significant at the intersections.
Hence pedestrian crossings on minor roads and major roads which affect the
right-turning movement of minor road vehicles were also extracted. Pedestrian
crossing on major road leg-2 and minor roads were recorded at an interval of 5
min to get hourly pedestrian crossings. The hourly pedestrian crossings at each
intersection were tabulated in Table 3.
Hourly pedestrian
crossing volume at each intersection
|
Intersection |
Road |
Sub Total (ped/hr) |
Total (ped/hr) |
|
I |
Major |
116 |
208 |
|
Minor |
92 |
||
|
II |
Major |
112 |
262 |
|
Minor |
150 |
||
|
III |
Major |
65 |
303 |
|
Minor |
238 |
||
|
IV |
Major |
27 |
170 |
|
Minor |
143 |
||
|
V |
Major |
40 |
83 |
|
Minor |
43 |
4.1 Occupation
time data
Occupation time is defined as the
time required to clear a conflict zone by the maneuvering vehicle (the time for
which the vehicle occupies the conflict area). Figure 3 illustrates the concept
of occupation time (the difference between time stamps at which a vehicle
approaches section AA and exits section BB). Occupancy time depends on
parameters such as intersection geometry, vehicle type, and driver behavior.
The advantage of using occupation time is that it takes into account non-lane
behavior, such as vehicles crossing an intersection in a zigzag pattern.
The procedure for extracting
occupation time data is identifying the Stop line from the video recorded, the
stop line will be determined based on the position where the majority of
vehicles stop. The time at which the vehicle arrives at the conflict area (ta) and departs from the
conflict area (td)
conflict area, as well as the vehicle type is noted. Difference between these
two times given Occupation Time as given in Equation 1.
![]() (1)
(1)
Where, Ot = Occupation
time, ta = vehicle arrival
time at the conflict area, tb = vehicle departure time from the
conflict area.
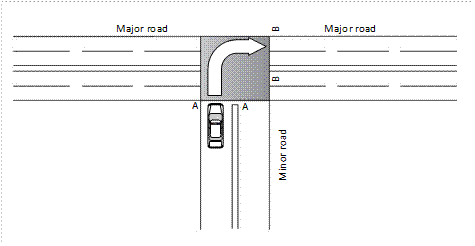
Fig. 3. Occupation time concept
The average occupation time at each
intersection is calculated and plotted as shown in Figure 4. Among all the
intersections, the average occupation time at the Erragattu
intersection is the highest, which is 11.49 seconds, due to reasons such as a
larger conflict area and a relatively higher proportion of heavy vehicles as
compared to other sites. The average occupation time at an intersection near
the Hanamkonda bus stand is the lowest since the
conflict area is very small at that intersection, also pedestrian flow and
conflicting volume are the lowest at the intersection. Though the conflict area
at Madikonda is also large, vehicles maneuver right
turns with a larger radius of turn to minimize the travel length in the
conflict zone, which resulted in a lower average occupancy time.
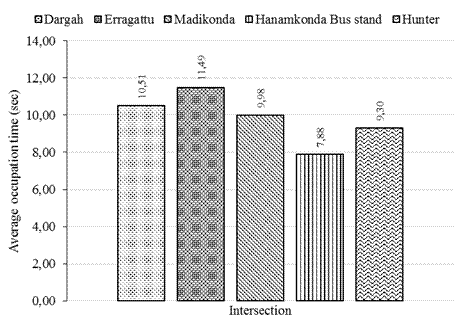
Fig. 4. Average occupation time at each intersection
The average occupation time for each
vehicle type at each intersection is shown in Figure 5.
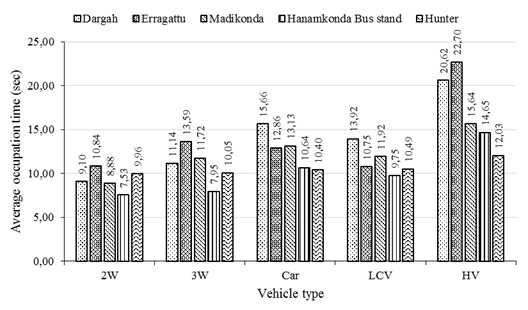
Fig. 5. Average occupation time (sec) for each vehicle type at each
intersection
Among all the vehicle types,
two-wheelers have the shortest occupation time since the maneuverability of
two-wheelers is high and they tend to encroach on the available spaces to clear
the conflicting area in a zig-zag pattern. Three-wheelers also have lower
occupation time due to ease of maneuvering while turning as well as their
aggressive nature when compared to other vehicle types. Cars and LCVs have
similar occupation times at all intersections. Heavy vehicles such as buses,
tractors, and HCVs have the highest occupation time because of the larger
lengths and lower speeds of heavy vehicles. ANOVA test is performed to check
whether a significant difference exists between occupation times of five different
vehicle groups. ANOVA test result is tabulated in Table 4.
Tab. 4
ANOVA test result
|
|
DF |
Sum of squares |
Mean squares |
F |
Pr > F |
|
Between groups |
4 |
2251 |
562.82 |
17.11 |
<0.0001 |
|
Within groups |
464 |
15261 |
32.89 |
||
|
Total |
468 |
17513 |
|
ANOVA test result indicated that a
significant difference exists between the occupation times of different groups.
The between-groups variance is significant (F = 17.11, p < 0.0001),
indicating substantial differences between vehicle groups. With a total of 468
degrees of freedom, the test confirms that vehicle type significantly impacts
occupation time. The maximum and minimum occupation time of each vehicle
category at each intersection is tabulated in Table 5.
Tab. 5
Minimum and maximum
occupation time at each intersection (sec)
|
Vehicle type |
Intersection |
|||||||||
|
I |
II |
III |
IV |
V |
||||||
|
Min |
Max |
Min |
Max |
Min |
Max |
Min |
Max |
Min |
Max |
|
|
2W |
2.88 |
32.04 |
3.12 |
39.26 |
3.36 |
32.82 |
2.31 |
28.36 |
2.03 |
36.25 |
|
3W |
4.36 |
31.99 |
4.47 |
44.06 |
5.49 |
38.50 |
2.96 |
26.96 |
4.87 |
32.74 |
|
Car |
4.67 |
32.79 |
4.26 |
38.21 |
3.84 |
29.80 |
3.84 |
24.14 |
3.77 |
29.27 |
|
LCV |
5.10 |
37.68 |
6.10 |
36.46 |
6.80 |
28.78 |
6.22 |
25.40 |
6.17 |
33.67 |
|
HV |
7.70 |
27.51 |
9.67 |
35.67 |
11.75 |
29.34 |
12.64 |
21.48 |
6.68 |
31.04 |
Table 5 presents the minimum and maximum occupation times in seconds for
various vehicle types at five intersections. Two-wheelers generally exhibit the
shortest times while heavy vehicles have the longest. The data highlights
significant variation in occupation times across vehicle types and
intersections emphasizing the influence of vehicle size and intersection
characteristics.
4.2 Effect of traffic attributes
The effect of different traffic and
geometric parameters such as conflicting flow estimated using HCM (2010), the proportion of heavy vehicles, and
Pedestrian flow on occupation time were studied, and significant variables are
identified from the correlation study.
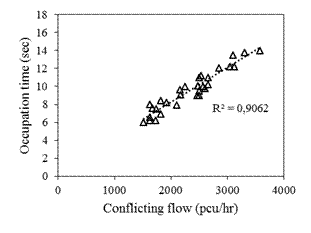
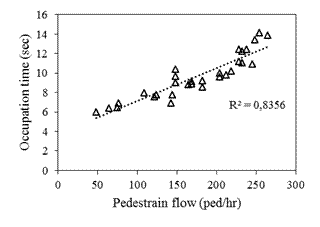
It is observed from Figure 6 that as
the conflicting flow increases, the available gaps in the conflicting flow
reduce and that results in more waiting time for vehicles in their minor approach,
thereby increasing their occupation time. Heavy vehicles in the conflicting
flow have a significant effect on the occupation time. Due to the large vehicle
size, the minor approach vehicles hesitate to enter the conflict area, this
phenomenon is more predominant in the case of small-sized vehicles. The effect
of the pedestrian crossing forces the minor approach vehicles to yield before
performing the right turn.
4.2.1 Modeling occupation time
Various parameters that affect
occupation time are tested for correlation and significance using correlation
analysis. To capture the effect of each parameter on occupation time models are
developed for the same dependent variable and traffic parameters as independent
variables using regression analysis. Multiple linear regression analysis is
performed to achieve the model. Out of data collected 70% of the data is used
to develop a model and the data remaining was used to validate the developed
model. The relation between the occupation time of right-turning vehicles from
a minor road and various traffic and geometric variables considered is modeled
and the same is presented in Equation 2.
![]() (2)
(2)
Where, Ot is occupation time in seconds, PHV is
percentage of heavy vehicles in conflicting flow, Cf is conflicting flow
in pcu/hr, Pf is pedestrian flow in
pedestrian flow in pedestrian crossings per hour.
|
|
|
|
|
|
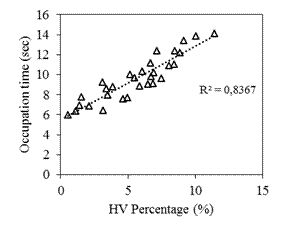
Fig. 6. Plot between occupation time and percentage of heavy vehicles in
the conflicting flow
The R2
value of the model is 0.95 and the standard error for the model is 0.5. The
coefficient of PHV
shows that as the proportion of heavy vehicles in the conflicting flow
increases, the average occupation time also increases. When a vehicle,
particularly small-sized vehicle is attempting to enter into the conflict area,
it yields whenever the conflicting vehicle is heavy vehicle, looking for a
larger gap. This results in increased average occupation time. Similarly, the
coefficient of conflicting flow implies that as conflicting flow increases, the
average occupation time would also increase due to the vehicle yielding to
higher priority movement before entering the conflicting area. As pedestrian
flow increases, vehicles of minor roads would yield to let the pedestrians
cross, thereby increasing the average occupation time, which illustrates the
coefficient of pedestrian flow considering a minimum approach width of a single
lane i.e., 3.3m.
4.2.2 Validation of the models
After the development of a model,
the validation process is an essential step that determines the extent to which
the model corresponds to a real system. The field occupation time was compared
with predicted occupation time as shown in Figure 7.
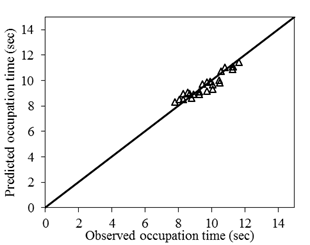
Fig. 7. Validation of
average occupation time model for right turning vehicles
The validation for the model
developed showed a good prediction of the average occupation time value, i.e.,
the predicted values of the average occupation time of tight turning vehicles
are close to the average occupation time in the field. The model's error and
accuracy assessment show a Root Mean Square Error of 1.12, indicating a small
average deviation between predicted and observed values.
4.3 Estimation of Gap acceptance
data
Gap acceptance is an essential
element of microscopic traffic characteristics, which can be used to determine
the capacity and delay at an uncontrolled intersection. A minor
road driver must decide whether or not a gap is large enough to safely execute
the desired maneuver when approaching an intersection with conflicting traffic
flows. In general, a driver rejects all gaps smaller than his or her critical
gap and accepts the remaining. Thereby, the critical gap is a criterion for
determining if a vehicle from a minor road can enter a major road; a
critical gap specifies the minimum value of gap that is acceptable to a driver.
There are various methods available for the estimation of a critical gap for a
movement at an unsignalized intersection. In the
present study, the Raffs method was used to estimate critical gaps because of
its wide popularity and simplicity of execution.
Reference lines are marked on major
and minor approaches. The time at which the subject vehicle, i.e., a vehicle
coming from a minor approach crosses the reference line is noted. Then, the
time at which the lead/follower vehicles coming from the major approach cross
the conflict point is noted. If vehicles from major approaches cross the
conflict point before the subject vehicle, then the respective Gap is
considered rejected. The Gap in which the subject vehicle crosses the conflict
point first is considered accepted. The same procedure is repeated for the
entire duration. The data was analyzed and the Number of accepted and rejected
gaps are calculated. A graph is plotted with a cumulative number of gaps
accepted and rejected on the y-axis and gap size on the x-axis. The Point of
intersection of these curves is taken as the critical gap, as shown in Figure
8.
From Figure 8, it can be observed
that the critical gap for minor right movement at III-intersection is 4.3
seconds. From the cumulative accepted and rejected curves, it can be noticed
that when the gap available was more than 8 seconds, the gap available is
mostly accepted. The critical gap was also determined for each vehicle type at
each intersection shown in Figure 9.
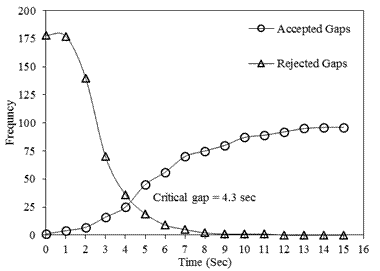
Fig. 8. Plot of cumulative accepted gap and rejected gap vs gap size at
III-intersection
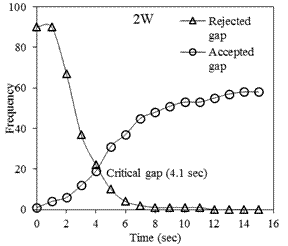
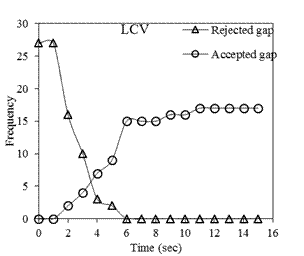
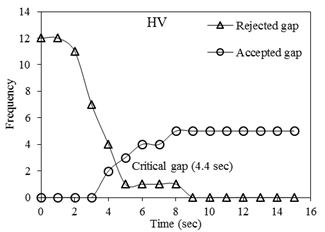
From Figure 9, it can be noticed
that the critical gap for two-wheelers is the smallest, which is 4.1 seconds.
Two-wheelers are small in size compared to other vehicles and due to their size
and ease of maneuverability, the critical gap for two-wheelers is the least.
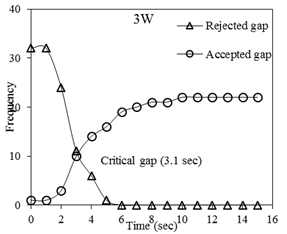
The critical gap for three-wheelers is also 3.1 seconds. Due to the aggressive
driving nature of the drivers of three-wheelers, they tend to accept smaller
gaps and sometimes force their entry to perform the right turning maneuver,
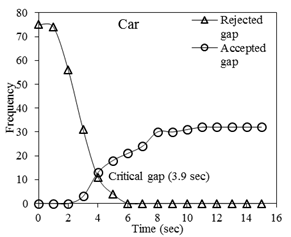
hence the smaller critical value. The critical gap value for cars and LCVs is
3.9 seconds and 3.6 seconds respectively, which is slightly large compared to
two-wheelers and three-wheelers. The critical gap for heavy vehicles is the
highest among all the vehicle types, which is 4.4 seconds, and it can also be
noted that they sometimes reject gap sizes as large as 9 seconds. This is due
to the difficulty in maneuvering heavy vehicles because of their large size.
Similar results were observed for
other intersections. The determined critical gap values and follow-up time are
tabulated as shown in Table 6. The follow-up was assumed to be 60 % of the
critical gap as established in several studies
Tab. 6
Critical gap values for
each vehicle type at each intersection
|
Vehicle type |
Critical gap (sec) at
Intersection |
Follow up time (sec)
at Intersection |
||||||||
|
I |
II |
III |
IV |
V |
I |
II |
III |
IV |
V |
|
|
2W |
3.1 |
3.4 |
4.1 |
3.4 |
3.3 |
1.86 |
2.04 |
2.46 |
2.04 |
1.98 |
|
3W |
3.2 |
4 |
4.3 |
3.4 |
3.8 |
1.92 |
2.4 |
2.58 |
2.04 |
2.28 |
|
Car |
3.9 |
5.3 |
5 |
5 |
3.9 |
2.34 |
3.18 |
3 |
3 |
2.34 |
|
LCV |
3.6 |
4 |
4.8 |
4.8 |
4.3 |
2.16 |
2.4 |
2.88 |
2.88 |
2.58 |
|
Overall |
3.3 |
3.8 |
4.3 |
3.5 |
3.6 |
1.98 |
2.28 |
2.58 |
2.1 |
2.16 |
|
|
|
||
|
|
Critical gap (3.6 sec) |
||
|
|
|||
Fig. 9. Plot of critical
gap estimation for vehicle types at I-intersection
4.4 Estimation of capacity
The capacity for right turning
movement from minor road is estimated at each intersection using Indo – HCM 2017 method. The capacity of a movement is determined
using the following Equation 3.
![]() (3)
(3)
Where Cx = capacity of movement (PCU/hr), Vc,x = Conflicting flow for movement (PCU/hr), tc,x = Critical gap
(sec), tf,x
= follow-up time (sec), a, b =
adjustment factors based on intersection geometry.
Conflicting flow is obtained from
the traffic count at each intersection. Follow-up time and critical gap values
were estimated using the Raff method at each intersection. The capacity
estimated at each intersection is shown in the Table 7.
Tab. 7
Capacity
|
Intersection |
Capacity (PCU/hr) |
|
I |
1292 |
|
II |
1224 |
|
III |
998 |
|
IV |
1403 |
|
V |
1563 |
Capacity for right turning movement
is highest at V-intersection due to lower values of critical gap and
conflicting flow. Similarly, capacity at IV-intersection is the lowest due to
higher critical gap at that intersection as a result of high conflicting flow
and pedestrian flow.
4.5
Relation between occupation time and capacity
From the MLR
models developed for occupation time, it is evident that occupation time is
highly dependent on the conflicting flow and heavy vehicle proportion. Similar
to the occupation time, the capacity of the movement also depends on the
conflicting traffic volume and the critical gap at the intersection, which in
turn depends on the conflicting flow, proportion of heavy vehicles etc. Hence,
it can be inferred that the occupation time and capacity at each intersection
are related. Therefore, the same is studied at each intersection and the graphs
plotted are shown in Figure 10.
It is evident that the capacity of
an intersection is highly correlated to occupation time at the intersection. It
can be observed that as the occupation time of the movement decreases, the
capacity of the same increases and vice versa. When occupation time for a
movement is high, vehicles need more time to clear that intersection. That is,
fewer ehicles clear the intersection in a given time
when occupation time is high, resulting in lower capacity for the movement. It
can be concluded that capacity is inversely correlated to occupation time. The
relationship between occupation time and capacity is presented in Equation 4.
![]() (4)
(4)
Where,
C = Capacity in pcu/hr, Ot =
Occupation time in sec.
The above equation can be used to
estimate the capacity of right-turning movement of minor approach at an
uncontrolled intersection the using average occupation time of the same
movement. Sensitivity analysis was performed to provide robustness of the model
and the magnitude of changes in capacity when occupancy time shifts due to
variations in conflicting traffic flow, heavy vehicle proportion and pedestrian
influence. The constant (-95.7) is considered as the rate of change or
sensitivity coefficient of capacity with respect to occupancy time. The sensitivity
analysis was performed using a baseline occupancy time and capacity of 10 sec
and, 1245 pcu/hr. A 10% decrease in occupancy time
increases capacity to 1340.70 pcu/hr. The sensitivity
analysis shows that capacity is highly sensitive to changes in occupancy time.
A small variation in occupancy time, whether due to increased conflicting
traffic flow, higher heavy vehicle proportions, or pedestrian volume, leads to
significant changes in intersection capacity. The model was validated using
field data as shown in Figure 11.
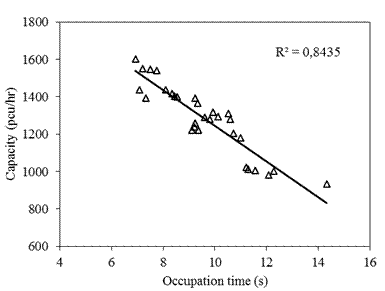
Fig. 10. Relation between occupation time and capacity
The average occupation time of the
movement obtained from Equation 2 can be substituted in Equation 4. This would
serve as a simpler approach to estimating capacity.
5.
CONCLUSIONS
Following are the conclusions obtained from the
results of the present study:
·
Two-wheelers have the lowest
occupation time among vehicle categories because their maneuverability is high
and they tend to squeeze into available spaces to clear the conflict area.
Three wheelers also have lower occupation time due to ease of maneuver while
turning as well as their aggressive nature when compared to other vehicle types
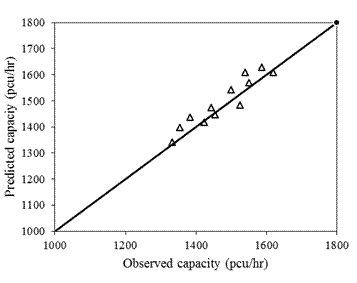
Fig. 11. Validation of
estimation of capacity for right turning traffic
·
Cars and LCVs have similar
occupation time at all the intersections. Heavy vehicles such as buses,
tractors and HCVs have the highest occupation time because of their larger
length and lower speed of heavy vehicles.
·
From the correlation analysis,
it was observed that the occupation time has a positive correlation with the
percentage of heavy vehicles in the conflicting flow, conflicting flow,
pedestrian flow and approach width and has a negative correlation with the
presence of median on minor road
·
There is an increase in
occupation time with an increase in conflicting flow. It is because as the
conflicting flow increases, the available gaps in the conflicting flow
decrease, resulting in increased waiting time for minor road vehicles to to
safely execute the desired maneuver, hence increasing their occupancy
time. It was observed that for every 5%
increase, occupation time increased by 0.2 sec
·
There is an increase in
occupation time with increase in % of heavy vehicles in the conflicting
flow. It is because when the size of
vehicles is large, drivers on the minor road are hesitant to enter the conflict
area to perform the desired movement and wait for a longer time resulting in
longer occupation time. It was observed that for every 1% increase, occupation time
increased by 0.35 sec.
·
There is an increase in
occupation time with an increase in approach width. It is because as the
approach width increases, the area of conflict increases and also the turning
radius decreases resulting in higher occupation time. It was observed that for
every 0.5m increase, the occupation time increased by 0.25 sec.
·
There is an increase in
occupation time with an increase in pedestrian flow. It is because as the
pedestrian crossings increase, it forces the minor road vehicles to yield
before performing the right turn there by increasing occupation time. It was
observed that for every 5% increase, the occupation time increased by 0.13 sec.
·
At every intersection,
two-wheelers have the lowest critical gap value, closely followed by three-wheelers.
Two-wheelers being smaller in size and easy to maneuver accept smaller gaps but
in the case of three-wheelers, they force their entry due to their aggressive
driving behavior and hence the lower critical gap.
·
The critical gap for heavy
vehicles is the highest among all the vehicle types. This is due to the
difficulty in maneuvering heavy vehicles because of their large size.
·
Capacity is found to be
negatively correlated with occupation time. It is because when the occupation
time of a movement is high, vehicles require more time to clear the
intersection, which implies that fewer vehicles clear the intersection in a
given amount of time, hence reducing the movement's capacity.
The findings highlight
the significant impact of these factors on occupation time and, consequently,
on intersection capacity. The results, particularly the linear regression model
developed, contribute to a better understanding of how mixed traffic interacts
at uncontrolled intersections, offering a more accurate method for capacity
estimation in such environments. The results of this study align with existing
literature by confirming the impact of conflicting flow, heavy vehicle
proportion, and pedestrian flow on intersection capacity. However, the study's
use of occupation time provides a more accurate capacity estimation in mixed
traffic conditions, addressing the limitations of traditional gap acceptance
models typically used in homogeneous traffic studies. This approach offers a
significant improvement in predicting real-world intersection performance under
complex traffic scenarios.
Despite the valuable
insights gained, this study has several limitations:
·
The study was conducted at
only five intersections within Warangal city. The results may not be
generalizable to intersections with different traffic compositions or in other
cities with different driving behaviors and road geometries.
·
The extraction of traffic data
from video recordings was performed manually. This process could introduce
biases or inaccuracies in the measurement of occupation time and vehicle
counts.
·
The study did not account for
all possible variables that could influence intersection capacity, such as
weather conditions, driver aggression levels, or variations in traffic patterns
on different days of the week.
Scope for future research are:
·
Expanding the Geographic
Scope: Conducting similar studies in various cities across different regions,
including rural and urban areas with varying traffic conditions, could help in
developing a more universally applicable model.
·
Implementing automated data
extraction techniques, such as machine learning algorithms or computer vision
tools, could enhance the accuracy and efficiency of data processing and reduce
potential biases.
·
Future studies could consider
a broader range of variables, including environmental factors, driver
psychology, and real-time traffic management interventions, to refine the
capacity estimation models further.
References
1. National Research Council (U.S.), HCM 2010; Highway Capacity Manual, Transoportation Research Board, 2010.
2.
Mohan
M., S. Chandra. 2018. "Critical gap estimation at two-way stop- controlled
intersections based on occupancy time data". Transportmetrica
A: Transport Science 14(4): 316-329.
3.
Asaithambi G., C. Anuroop.
2016. "Analysis of occupation time of vehicles at urban unsignalized intersections in non-lane-based mixed traffic
conditions". Journal of Modern Transportation 24: 304-313.
4.
Ashalatha R., S. Chandra. 2011. "Critical gap
through clearing behaviour of drivers at unsignalized intersections". KSCE
Journal of Civil Engineering 15(8): 1427-1434.
5.
Chandra
S., A. Agrawal, A. Rajamma.
2009. "Microscopic
Analysis of Service Delay at Uncontrolled Intersections in Mixed Traffic
Conditions". Journal of Transportation Engineering 135(9): 323-329.
6.
Pawar N.M., N. Gore, S.S. Arkatkar.
2022. "Examining Crossing Conflicts by Vehicle Type at Unsignalized
T-Intersections Using Accepted Gaps: A Perspective from Emerging
Countries". Journal of Transportation Engineering, Part A: Systems
148(6).
7.
Mohan
M., S. Chandra. 2021. "Investigating the influence of conflicting flow’s
composition on critical gap under heterogeneous traffic conditions". International
Journal of Transportation Science and Technology 10(4): 393-401.
8.
Dutta
M., M.A. Ahmed. 2018. "Gap acceptance behaviour
of drivers at uncontrolled T-intersections under mixed traffic
conditions". Journal of Modern Transportation 26: 119-132.
9.
Abhigna
D., M. Ramees, K.V.R. Ravishankar. 2018. "Effect of Gap Acceptance Behaviour of the Right Turning Vehicles on the Major Road
Stream for Uncontrolled Three-Legged Intersections under Mixed Traffic
Conditions". International Journal of Engineering 31(6): 870-876.
10.
Amin
H.J., A.K. Maurya. 2015.
"A review of critical gap estimation approaches at uncontrolled
intersection in case of heterogeneous traffic conditions". Journal of
Transport Literature 9(3): 5-9.
11. Maurya A.K.,
H.J. Amin, A. Kumar. 2016. "Estimation of Critical Gap for Through
Movement at Four Leg Uncontrolled Intersection". Transportation
Research Procedia 17: 203-212.
12. Patil G.R.,
D.S. Pawar. 2014. "Temporal and Spatial Gap
Acceptance for Minor Road at Uncontrolled Intersections in India". Journal
of Transportation Research Record 2461(1): 129-136.
13.
Troutbeck R.J. 2014. "Estimating the Mean Critical
Gap". Journal of Transportation Research Record 2461(10): 76-84.
14.
Kaysi
I., G. Alam. 2000. "Driver Behaviour
and Traffic Stream Interactions at Unsignalized
Intersection". Journal of Transportation Engineering 126(6):
498-505.
15. Asaithambi G., T. Aswini.
2022. "Capacity Analysis of Uncontrolled Intersections with and Without
Pedestrian Cross Flow in Mixed Traffic Conditions". Transportation in
Developing Economies 8(20).
16. Ruskic N., V. Mirovic.
2021. "Estimation of left-turn capacity at the unsignalized
intersection". Simulation Modelling Practice and Theory 106.
17. Amarnatha G.A., N. Manjunatha, K.S. Reddy. 2018.
"Capacity Analysis of Un-signalized Intersection: A Case Study of City
Junction". International Journal of Engineering Research Technology
7(6).
18. Prasetijo J., W. Razzaly,
N. Wu, K. Ambak, M.E. Sanik,
M.M. Rohani, H. Ahmad. 2014. "Capacity Analysis
of Priority Intersections with Flare under Mixed Traffic Conditions". Procedia
- Social and Behavioural Sciences 138: 660-670.
19. Li H., W. Deng, Z. Tian, P. Hu.
2009. "Capacities of Unsignalized Intersections
under Mixed Vehicular and Nonmotorized Traffic
Conditions". Transportation Research Record 2130(1): 129-137.
20. Shi F., H. Li. 2008. "The
Influence of Non-Motorised Streams on Capacities of
Vehicular Streams at Unsignalized
Intersections". Proceedings of IEEE 978(1): 2004-2008.
21. Prasetijo J. 2005. "Development of a New
Method of Capacity Analysis at Unsignalized
Intersections Under Mixed Traffic Flow". Proceedings
of Eastern Asia Society of Transportation Studies 5: 967-983.
22.
Chodur J. 2005. "Capacity Models and Parameters
for Unsignalized Urban Intersections in Poland".
Journal of Transportation Engineering 131(12): 924-930.
23. Li W., W. Wang, D. Jiang. 2003. "Capacity of Unsignalized Intersections with Mixed Vehicle Flows". Transportation
Research Record 1852(1): 265-270.
24.
Pollatschek M.A., A. Polus, M. Livneh.
2002. "A decision model for gap acceptance and capacity at
intersections". Transportation Research Part B: Methodological
36(7): 649-663.
25. Brilon W., N. Wu. 2001. "Capacity at Unsignalized Intersections Derived by Conflict Technique".
Transportation Research Record 1776(1): 82-90.
26. Tian Z., R. Troutbeck,
M. Kyte, W. Brilon, M. Vandehey, W. Kittelson, B.
Robinson. 2000. "A further investigation on critical gap and follow up
time". In: Fouth International
Symposium on Highway Capacity, Transportation Research Board. Maui, Hawaii.
Received 14.08.2024; accepted in
revised form 20.11.2024
![]()
Scientific Journal of Silesian University of Technology. Series
Transport is licensed under a Creative Commons Attribution 4.0
International License