Article citation information:
Protsenko, V., Malashchenko, V., Nastasenko, V., Babiy, M., Voitovych, O. Elevator drum-pad brake mechanisms: redundant constraints and reliability rise opportunity. Scientific Journal of Silesian University of Technology. Series Transport. 2024, 125, 229-242. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2024.125.15.
Vladyslav PROTSENKO[1], Volodymyr MALASHCHENKO[2], Valentyn NASTASENKO[3], Mykhailo BABIY[4], Olha VOITOVYCH[5]
ELEVATOR
DRUM-PAD BRAKE MECHANISMS: REDUNDANT CONSTRAINTS AND RELIABILITY RISE
OPPORTUNITY
Summary. The article deals with
mechanical engineering, and transport machines, namely the elevator brake
mechanism structure. The article aims to study the number and location of
redundant constraints in elevator brake mechanisms and to depict their impact
on brake reliability and transportation safety. To study the structure of the
mentioned mechanisms, we used classical methods of applied mechanics plus the
circuit method of L. Reshetov. The structure of crane
disc brakes with short-stroke DC electromagnet and long-stroke AC electromagnet
mechanisms was analyzed and redundant constraints
were identified. It was shown that the presence of redundant constraints causes
friction torque oscillation and lead to load distribution unevenness between
brake elements. Based on the provided analysis,
construction improvement events should be implemented to remove the most
dangerous redundant constraints.
Keywords: drum-pad brake, redundant constraint; mechanism,
friction torque, reliability, self-alignment
1. INTRODUCTION
The reliability of the braking
system has a significant influence on transportation safety, which is vital for
automotive vehicles and other transport systems intended for transporting
people. The operational safety of an elevator directly depends on reliability
of the brake mechanism, especially considering the possibility of gearbox
self-braking loss. Disc-pad brakes are widespread in cars and lifting
equipment, and in heavy-loading systems, such as elevators, drum-type brakes
are also used. This explains the interest in studying ways to increase the
reliability of brake systems. In recent years, elevator accidents have often
occurred. The main factor of these accidents was the fault of brake mechanisms
[1]. The latest research has focused on identifying low-reliability elements in
brake systems using goal-oriented methodologies [2], investigation of safety
risks [3], brake capacity study [4], and identification of brakes noise and
vibration characteristics [5]. Nowadays, drum-pad type brakes are widespread in
cranes and elevators. Their characteristic drawback is overheating, which
determines a certain amount of modern scientific research in the field of their
dynamics [6], parts temperature distribution [7] and friction elements wear
features [8]. Based on new studies, new materials [9] and brake mechanisms
operation principles [10] are being proposed and researched.
Typically, in drum-pad brakes, to
increase safety, each pad can independently press the drum with the levers.
This reserve can be leveled by uneven loading of the pads due to driving or
brake parts dissymmetry. Therefore, increasing the reliability of brakes by
ensuring the possibility of pads self-aligning is a reserve for improving the
safety of the operation of elevators and other similar machines. One of the
main parts of elevator brakes are lever mechanisms, the accuracy of which
determines their operating parameters [11], namely the brake release response
time [12].
The presence of redundant
constraints in the mechanisms contributes to the increase in the unevenness of
the load distribution between the parts [13]. This can lead to the destruction
of parts, increased requirements for manufacturing and assembling accuracy
[14], and an increase in mechanical losses [15]. There are not many works
dedicated to the study of the structure and elimination of redundant
constraints in elevator brake mechanisms. For example, the lever mechanisms of
crane drum-pad brakes with electrohydraulic and electromagnetic actuators were
considered [16], but these elements themselves were not taken into account when
compiling the structural diagram of the brake, and the structure of elevator
brakes with independent pressing pads remains under-researched today.
2. METHODOLOGY
Currently, the two most widespread types
of drum-pad brakes in elevators are those with a short-stroke DC electromagnet
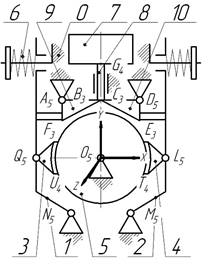
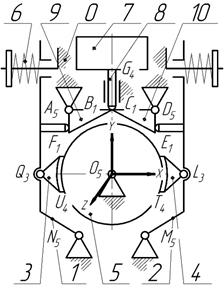
(Fig. 1) and those with long-stroke AC electromagnet (Fig. 2).
The brake mechanism in Fig. 1, b,
contains the left 1 and right 2 braking levers, hingedly
(with rotary joints M5
and N5)
connected to the base 0. Pads 3 and 4 are connected with rotary joints Q5 and
L5
to levers 1 and 2 and have the ability to cover drum 5 with their cylindrical
surfaces (T4,
U4).
When the brake pads 3 and 4 are closed against drum 5 pressure is provided by
springs 6. Brake opening is provided by a short-stroke DC electromagnet 7,
whose rod 8 can interact with rockers 9 and 10 (B3 and C3
connections) allowing axial and rotary slide relative to the base 0 (through G4
joint). Rockers 9 and 10 are connected to the base 0 with A5 and D5
rotary joints and are able to interact with braking levers 1 and 2 through
connections F3
and E3.
Drum 5 is fixed relatively to the base 0 with rotary joint O5.
|
|
|
|
|
a) |
b) |
|
|
Fig. 1. Elevator brake with short-stroke DC
electromagnet: general view (a) and structural diagram (b) |
||
|
|
|
|
|
a) |
b) |
|
|
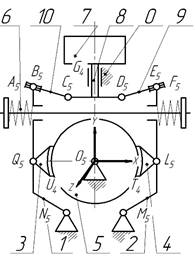
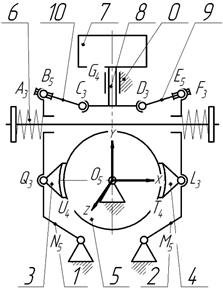
Fig. 2. Elevator brake with long-stroke AC
electromagnet: general view (a) and structural diagram (b) |
||
The brake mechanism shown in Fig. 2,
b, contains the left 1 and right 2 braking levers, which are hingedly (with rotary joints M5 and N5)
connected to the base 0. Pads 3 and 4 are connected with rotary joints Q5 and
L5
to levers 1 and 2 and they can cover drum 5 with their cylindrical surfaces (T4, U4).
When the brake pads 3 and 4 are closed against the drum 5 pressure is provided
by springs 6. Brake opening is provided by a long-stroke AC electromagnet 7,
whose rod 8 is connected with levers 1 and 2 through beams 9 and 10 using A5, B5, C5, D5, E5, F5
rotary joints. The drum 5 is fixed relative to the base 0 with rotary joint O5.
Firstly, we consider the structure
of the brake mechanism with a short-stroke DC electromagnet (Fig. 2, b). It
contains eight movable links (n = 8).
The number of 5-class kinematic pairs is P5 = 7 (А5, D5, L5, M5, N5, О5, Q5), the number of
4-class kinematic pairs is P4 = 3 (G4, T4, U4), the number of 3-class kinematic pairs is P3 = 4
(B3,
C3,
E3,
F3),
number of 2, and 1-class kinematic pairs is P2 = P1 =
0.
The total number of kinematic pairs
is:
|
P = P5 + P4 + P3 + P2 + P1 = 7 + 3 + 4 + 0 + 0 = 14 |
(1) |
The sum of kinematic pairs’ movabilities
[17]:
|
f = 1P5 + 2P4 + 3Pз + 4P2 + 5P1 = 1×7 + 2×3 + 3×4 + 4×0 + 5×0 = 25 |
(2) |
The number of independent locked circuits by Gohman formula [18]:
|
|
(3) |
Independent locked circuits are the following –
N5Q5U4О5N5;
M5L5T4О5M5;
N5F3A5N5;
M5E3D5M5;
A5B3G4A5;
D5C3G4D5.
Total mechanism mobility W = Wb + Wl = 1
+ 1 = 2,
where Wb = 1 – basic mechanism
mobility (drum 5 rotation);
Wl = 1 – local links
mobility (rod 8 around own axis rotation).
Then the number of redundant
constraints in basic variant by Somov and Malyshev formula:
|
|
(4) |
Redundant constraints number by Ozols formula
[19]:
|
|
(5) |
Thereby, the total redundant
constraints number in the analyzed mechanism q=qSM=qOZ=13.
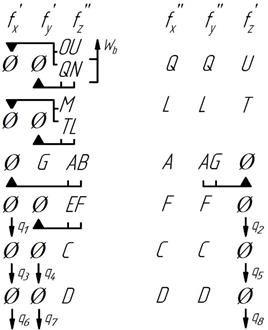
Using the circuit method [20] confirms the
presented calculations (Table 1).
Tab. 1
Circuit method application to basic brake with
short-stroke
DC electromagnet mechanism (Fig. 1)
|
Circuit |
Planar movabilities fp |
Non-planar movabilities fn |
|
|
|
|||
|
N5Q5U4О5N5 |
|||
|
M5L5T4О5M5 |
|||
|
N5F3A5N5 |
|||
|
M5E3D5M5 |
|||
|
A5B3G4A5 |
|||
|
D5C3G4D5 |
|||
|
|
|||
The identified redundant constraints
prevent the self-installation of brake pads on the surface of the braking drum
and can lead to overloading of the mechanism’s link (Table 2).
Tab. 2
Redundant constraints presence in the basic
brake with short-stroke
DC electromagnet mechanism (Fig. 1) consequences
|
Redundant constraint |
Influence of Redundant constraint presence |
Practical way of redundant constraint
influence leveling |
Leveling absence consequences |
|
1 |
2 |
3 |
4 |
|
q1 |
Impossibility of braking pads self-aligning
along X axis ( |
Control and limitation radial and angular
misalignment of braking pads and drum along and around X and Y axes. This
leads to an increase in the labor-intensiveness of brake assembling and
maintenance. Radial gap in joints L
and Q increases. This leads to
delayed brake activation, strokes, and vibrations during the elevator start
process. |
Braking pads overlay uneven load and wear
among themselves. Braking levers and springs experience uneven load. |
|
q4 |
|||
|
q2 |
Impossibility of braking pads self-aligning
around X axis ( |
Braking pads overlay uneven load and wear
along their width. Additional loading of braking levers and shafts by bending
moment in the YZ plane. |
|
|
q5 |
|||
|
q3 |
Impossibility of braking pads self-aligning
around Y axis ( |
Braking pads overlay uneven load and wear
along their width. The additional load of braking levers by torque and shafts
by bending moment in the XZ plane. |
|
|
q6 |
|||
|
q7 |
Impossibility of rockers self-aligning along X axis ( |
Fitting of contact surfaces of kinematic
pairs E and F by scraping. This leads to an increase in the
labor-intensiveness of brake assembling and maintenance. |
Non-simultaneous withdrawal of braking pads
from the drum leads to strokes and vibrations during the elevator start
process. |
|
q9 |
|||
|
q8 |
Impossibility of rockers and braking levers
self-aligning around Y axis |
The additional load of braking levers by
torque in the XZ plane. |
|
|
q10 |
|||
|
q12 |
Impossibility of right rocker self-aligning
along Y axis ( |
Fitting of the contact surface of kinematic
pair C by scraping. This leads to
an increase in the labor-intensiveness of brake assembling and maintenance. |
Non-simultaneous withdrawal of braking pads from
the drum leads to strokes and vibrations during the elevator start process. |
|
q11 |
Impossibility of rockers self-aligning around
X axis ( |
Fitting of contact surfaces of kinematic pair
C and B by scraping. The radial gap in joints A and D increases. This
leads to the increase in the labor-intensiveness of brake assembling and
maintenance. |
The most dangerous among the
identified redundant constraints belong to power circuits
q1…q6 which initiate the main disadvantage of the brake
mechanism (Fig. 1) – the impossibility of brake pads on drum self-alignment. In
addition to those listed in Table 1, this can lead to the creation of braking
forces even in an opened brake due to the presence of drum radial beating
and/or angular misalignment. Another disadvantage is the creation of a
cyclically variable friction moment by the closed brake in the presence of disk
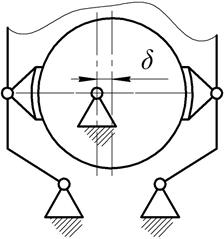
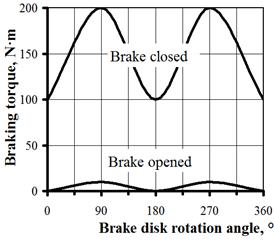
radial beating (Fig. 3), which can lead to oscillations (Fig. 4) and a decrease
in the fatigue strength of the drive parts.
|
|
|
|
Fig. 3. Braking drum radial beating δ influence |
Fig. 4. Approximate influence of the drum
beating on the brake friction torque in redundant constraints presence |
The mechanism of the brake with a long-stroke
AC electromagnet (Fig. 2, b) contains eight movable links (n = 8). The number of 5-class kinematic pairs here is P5 = 11 (А5, B5, C5,
D5, E5, F5,
L5, M5, N5,
О5, Q5), number of 4-class kinematic pairs is P4 = 3 (G4, T4,
U4), number of 3, 2 and
1-class kinematic pairs is P3
= P2 = P1 = 0.
The total number of kinematic pairs is:
|
P = P5 + P4 + P3 + P2 + P1 = 11 + 3 + 0 + 0 + 0 = 14 |
(6) |
The sum of kinematic pairs’ movabilities:
|
f = 1P5 + 2P4 + 3Pз + 4P2 + 5P1 = 1×11 + 2×3 + 3×0 + 4×0 + 5×0 = 17 |
(7) |
Number of independent locked circuits by Gohman
formula:
|
|
(8) |
Independent
locked circuits are as follows – N5A5B5C5G4N5;
M5F5E5D5G4M5;
N5Q5U4О5N5;
M5L5T4О5M5;
M5E2D5M5;
O5U4Q5A5B5C5G4O5;
O5T4L5F5E5D5G4O5.
Total mechanism mobility W = Wb + Wl = 1
+ 0 = 1,
where Wb = 1 – basic mechanism
mobility (drum 5 rotation);
Wl = 0 – local links
mobilities.
Then the redundant constraints
number in the basic variant by Somov and Malyshev formula:
|
|
(9) |
Redundant constraints number by Ozols formula:
|
|
(10) |
The circuit method confirms the
presented calculations (Table 3). The influence of the identified redundant
constraints is described in Table 4.
Tab. 3
Circuit method application to basic brake with
long-stroke
AC electromagnet mechanism (Fig. 2)
|
Circuit |
Planar movabilities fp |
Non-planar movabilities fn |
|
|
|
|||
|
N5Q5U4О5N5 |
|||
|
M5L5T4О5M5 |
|||
|
N5A5B5C5G4N5 |
|||
|
M5F5E5D5G4M5 |
|||
|
O5U4Q5A5B5C5G4O5 |
|||
|
O5T4L5F5E5D5G4O5 |
|||
|
|
|||
Tab. 4
Concequences of Redundant constraints іn basic brake with long-stroke
AC electromagnet mechanism (Fig. 2)
|
Redundant constraint |
Influence of Redundant constraint presence |
Practical way of redundant constraint
influence leveling |
Leveling absence consequences |
|
1 |
2 |
3 |
4 |
|
q1 |
Impossibility of braking pads self-aligning
along X and Y axis |
Control and limitation of radial and angular
misalignment of braking pads and drum along and around X and Y axes. This
leads to an increase in the labor-intensiveness of brake assembling and
maintenance. Radial gap in joints L
and Q increases. This leads to
delayed brake activation, strokes, and vibrations during the elevator start
process. |
Braking pads overlay uneven load and wear
among themselves. Braking levers and springs experience uneven load. |
|
q2 |
|||
|
q5 |
|||
|
q3 |
Impossibility of braking pads self-aligning
around X axis ( |
Braking pads overlay uneven load and wear
along their width. Additional loading of braking levers and shafts by bending
moment in the YZ plane. |
|
|
q6 |
|||
|
q4 |
Impossibility
of braking pads self-aligning around Y
axis ( |
Braking
pads overlay uneven load and wear along their width. The additional load of
braking levers by torque and shafts by bending moment in the XZ plane. |
|
|
q7 |
|||
|
Impossibility
of circuits N5A5B5C5G4N5;
M5F5E5D5G4M5;
O5U4Q5A5B5C5G4O5;
O5T4L5F5E5D5G4O5
assembling without tension: |
|
|
|
|
q8, q12, q16, q20 |
- along Z axis ( |
Radial gap in joints A, B, C, D,
E, F increases. This leads to
delayed brake activation, strokes, and vibrations during the elevator start
process. |
Additional loads of braking levers and beams
during the brake opening period. |
|
q11, q15, q17, q19 |
- around Y axis ( |
||
|
q14, q18 |
- around X axis ( |
||
|
q10, q13, q17 |
- along Y axis ( |
||
|
q9 |
- along X axis ( |
||
As can be seen, the most dangerous
are also q1…q7 redundant constraints
which initiate the same effect as in previous construction with a DC
electromagnet because they belong to power circuits in both types of brakes.
Other constraints belong to control circuits and are not as harmful, especially
when using a variable frequency drive.
3. RESULTS AND DISCUSSION
The main way to eliminate the
detected redundant constraints without intentionally introducing errors into
the design or worsening brake performance is to add mobilities to the mechanism
circuits by increasing the classes of kinematic pairs. For both of brake types,
it is promising to implement spherical pairs L3 and Q3
instead of rotary ones (L5,
Q5). For brakes with a
short-stroke DC electromagnet, it is also useful to modify joints B, C,
E, F by making their tips spherical and turning these pairs class from
3-rd to 1-st "sphere-plane" pairs (Fig. 5). For brakes with
long-stroke AC-electromagnet, spherical joints can be applied in kinematic
pairs A, C, D, F turning their class from 5th to 3rd (Fig. 6).
|
|
|
|
Fig.
5. Modified mechanism for brake with DC short-stroke electromagnet |
Fig
6. Modified mechanism for brake with AC long-stroke electromagnet |
For the modified short-stroke
DC-electromagnet brake mechanism (Fig. 5), with an unchanged total number of
links, kinematic pairs and circuits, the number of kinematic pairs of the
5-class became P5 = 5 (А5, D5, M5,
N5, О5), number of 4-class kinematic pairs
P4 = 3 (U4, T4, G4),
3-class kinematic pairs is P3
= 2 (L3, Q3), 1-class kinematic pairs
number is P1 = 4 (B1, C1, E1,
F1), 2-class kinematic
pairs number is P1 = 0.
The sum of kinematic pairs’
movabilities:
|
f = 1P5 + 2P4 + 3Pз + 4P2 + 5P1 = 1×5 + 2×3 + 3×2 + 4×0 + 5×4 = 37 |
(11) |
Total mechanism mobility W = Wb
+ Wl
= 1 + 1 = 2,
where Wb
= 1 – basic mechanism mobility (disc 7 rotation);
Wl
= 1 – local links mobility (rod 8 around own axis rotation).
Then, the number of redundant
constraints in the basic variant by Somov and Malyshev formula:
|
|
(12) |
Redundant constraints number by Ozols formula:
|
|
(13) |
The application of the circuit
method for the described variant of structural diagram modification is shown in
the Table 5, confirming the obtained results.
Tab. 5
Circuit method application to a modified
mechanism for brake with
DC short-stroke electromagnet (Fig. 5)
|
Circuit |
Planar movabilities fp |
Non-planar movabilities fn |
|
|
|
|||
|
N5Q3U4О5N5 |
|||
|
M5L3T4О5M5 |
|||
|
N5F1A5N5 |
|||
|
M5E1D5M5 |
|||
|
A5B1G4A5 |
|||
|
D5C1G4D5 |
|||
|
|
|||
For the modified long-stroke
AC-electromagnet brake mechanism (Fig. 6), with an unchanged total number of
links, kinematic pairs and circuits, the number of kinematic pairs of the
5-class became P5 = 5 (B5, E5, M5,
N5, О5), number of 4-class kinematic pairs
is P4 = 3 (U4, T4, G4),
3-class kinematic pairs is P3
= 6 (A3, C3, D3, F3,
L3, Q3), 2-class and 1-class kinematic pairs number P2 = P1 = 0.
The sum of kinematic pairs’
movabilities:
|
f = 1P5 + 2P4 + 3Pз + 4P2 + 5P1 = 1×5 + 2×3 + 3×6 + 4×0 + 5×0 = 29 |
(14) |
Total mechanism mobility W = Wb
+ Wl
= 1 + 0 = 1,
where Wb
= 1 – basic mechanism mobility (disc 7 rotation);
Wl = 0 – local links
mobilities.
Then, the number of redundant
constraints in the basic variant by Somov and Malyshev formula:
|
|
(15) |
Redundant constraints number by Ozols formula:
|
|
(16) |
The application of the circuit method, as shown
in Table 6, confirms the obtained results.
Tab. 6.
Circuit method application to a modified
mechanism for brake with
AC long-stroke electromagnet (Fig. 6)
|
Circuit |
Planar movabilities fp |
Non-planar movabilities fn |
|
|
|
|||
|
N5Q3U4О5N5 |
|||
|
M5L3T4О5M5 |
|||
|
N5A3B5C3G4N5 |
|||
|
M5F3E5D3G4M5 |
|||
|
O5U4Q3A3B5C3G4O5 |
|||
|
O5T4L3F3E5D3G4O5 |
|||
|
|
|||
4. CONCLUSIONS
The structure of braking devices
mechanisms in transport vehicles and devices significantly affects their
reliability and safety of operation. This article proposes measures to improve
the structural integrity of elevator brakes, especially those intended for
transporting people. The structure of crane disc brakes with short-stroke DC
electromagnet and long-stroke AC electromagnet mechanisms is analyzed and
redundant constraints are identified. Based on this analysis, construction
improvement events are suggested to eliminate the most dangerous redundant
constraints.
The performed theoretical studies
made it possible to establish the following:
- structural analysis of the basic mechanisms of the
elevator drum-pad brakes showed that the mechanism of the brake with
short-stroke DC electromagnet contains q
= 13 and the mechanism of the brake with long-stroke AC electromagnet contains q = 20 redundant constraints;
- it is shown
that the most dangerous, among identified, redundant constraints are in power
circuits because they initiate the main disadvantages of brake mechanism – the
impossibility of brake pads self-aligning on the drum. This can lead to the
creation of braking forces even in an opened brake as a result of the presence
of the drum radial beating and/or angular misalignment or the creation of a
cyclically variable friction moment by a closed brake, which can lead to
oscillations and a decrease in the fatigue strength of the drive parts;
- compensation for the presence of redundant connections
is usually performed by increasing the gaps in the kinematic pairs, which leads
to delayed brake activation, strokes, and vibrations in the elevator start
process;
- possible variants for modifying the structure of the
mechanisms for both brake types are proposed, which will reduce the redundant
constraints from q = 13 to q = 1 for the short-stroke DC
electromagnet brake, and from q = 20
to q = 10 for the long-stroke AC
electromagnet brake;
- the developed
technical solutions can be implemented in production without significant
complications.
References
1.
Liang X. 2017. “Failure
Mechanism Analysis of Elevator Brake”. 4th
International Conference on Machinery, Materials and Computer (MACMC 2017):
405-409.
2.
Vu N.-T., L.-D. Phan,
V.-D. Nguyen, Q.-B. Vu. 2021. “Research of
Determining Low-Reliability Elements of Multiple-Flows Compressed Air Braking
System Based on Goal-Oriented (GO) Methodology”. International Journal of Automotive and Mechanical Engineering 18(2):
8814-8824. DOI: 10.15282/ijame.18.2.2021.19.0675.
3.
Ren Zh. 2022. “The
Performance Analysis of Elevator Brake”. Journal
of Physics: Conference Series 2463: 012047. DOI: 10.1088/1742-6596/2463/1/012047.
4.
Peng
Q., Zh. Li,
H. Yuan, G. Huang,
S. Li,
X. Sun.
2018. “A Model-Based Unloaded Test Method for Analysis of Braking Capacity of
Elevator Brake”. Advanced in Material Science
and Engineering 2018: 1-10. DOI:
10.1155/2018/8047490.
5.
Magaswaran K.,
A.S. Phuman Singh, M.Z. Hassan. 2022. “A New Method in the Identification of
Noise and Vibration Characteristics of Automotive Disk Brakes in the Low
Frequency Domain”. International Journal
of Automotive and Mechanical Engineering 9: 1564-1577. DOI:
10.15282/ijame.9.2013.7.0129.
6.
Slavchev Y., L.
Dimitrov, Y. Dimitrov. 2018. “3-D Computer research and comparative analysis of
dynamic aspects of drum brakes and caliper disc brakes”. Archive of Mechanical Engineering 2: 253-276. DOI: 10.24425/123024.
7.
Yevtushenko A., K. Topczewska, M. Kuciej. 2021. “Analytical determination of the brake
temperature mode during repetitive short-term braking”. Materials 14: 1912. DOI: 10.3390/ma14081912.
8.
Ungureanu
M., N. Medan,
S. Ungureanu,
K. Nadolny 2022. “Tribological Aspects
Concerning the Study of Overhead Crane Brakes”. Materials 15: 6549. DOI: 10.3390/ma15196549.
9.
Sahari B.B., M.M.
Shahzamanian, M. Bayat, Z.N. Ismarrubie, F. Mustapha. 2022. “Comparison of
Thermoelastic Results in Two Types of Functionally Graded Brake Discs”. Int. J. Automot. Mech. Eng. 5: 660-669. DOI: 10.15282/ijame.5.2012.12.0053.
10. Satyajit R.P., M.S. Suresh. 2022. “Experimental
Studies on Magnetorheological Brake for Automotive Application”. International Journal of Automotive and
Mechanical Engineering 15(1): 4893-4908. DOI: 10.15282/ijame.15.1.2018.2.0381.
11. Zalyubovskii M.G., I.V. Panasyuk. 2020. “On the Study
of the Basic Design Parameters of a Seven-Link Spatial Mechanism of a Part
Processing Machine”. International
Applied Mechanics 56: 54-64. DOI: 10.1007/s10778-020-00996-x.
12. Wang Bo. 2024. “Study on the Performance Test Method
of the Elevator Brake”. Mechatronics and
Automation Technology 46: 636-645. DOI: 10.3233/ATDE231158.
13. Zdanevich S.S., R.P. Pogrebnyak, S.V. Zdanevich. 2018.
“Structural analysis and rational design of mechanisms of cross-roll tube
straightening machines”. Science and
Transport Progress. Bulletin of Dnipropetrovs'k National University of Railway
Transport 5(77): 65-73. DOI:
10.15802/stp2018/147630.
14. Sydorenko I., E. Kravtsov, I. Prokopovych. 2019. “Reducing
the Reliability of Equipment as a result of the Reduction of the Culture of
Production”. Proceedings of Odessa
Polytechnic University 3: 5-13. DOI: 10.3390/ma15196549.
15. Pogrebnyak R.P. 2015. “Structural analysis and
rational design parallelogram arm gripping”. Metallurgy Theory and Practice 1-2: 123-125. DOI: 10.15802/stp2018/140547.
16. Smirnov G.F., P.I. Shtitsko, A.P. Ivanova. 2007. “Redundant
constraints in crane drum-pad brakes”. Lifting
and Transport Technique 2: 101-114.
17. Mata S.A., A.B. Torras, J.A. Cabrera et al. 2016. Fundamentals of
Machine Theory and Mechanisms. Cham:
Springer.
18. Kolovsky M.Z., A.N. Evgrafov, Yu.A. Semenov, et al.
2000. Advanced theory of mechanisms and
machines. Berlin: Springer.
19.
Ozols O.G. 1984. Theory of Mechanisms and Machines. Moscow:
Nauka.
20.
Reshetov L. 1986. Self-Aligning Mechanisms. Moscow:
Mir Publishers.
Received 01.08.2024; accepted in revised form 22.10.2024
![]()
Scientific
Journal of Silesian University of Technology. Series Transport is licensed
under a Creative Commons Attribution 4.0 International License