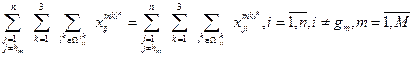Article citation information:
Onyshchenko, S., Berestenko, V., Melnyk, O., Onishchenko, O., Fomin, O., Kravchenko, O., Demidiuk, O. Integrated optimization models for carrier selection and route planning in multimodal transport systems. Scientific Journal of Silesian University of Technology. Series Transport. 2024, 125, 213-228. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2024.125.14.
Svitlana ONYSHCHENKO[1], Viktor
BERESTENKO[2], Oleksiy
MELNYK[3], Oleg ONISHCHENKO[4], Oleksij FOMIN[5], Oleksandra KRAVCHENKO[6], Oleksandr DEMIDIUK[7]
INTEGRATED
OPTIMIZATION MODELS FOR CARRIER SELECTION AND ROUTE PLANNING IN MULTIMODAL
TRANSPORT SYSTEMS
Summary. This paper presents a comprehensive
approach to the optimization of carrier routes and warehouses within multimodal
transport systems, with a focus on a localized approach that takes into account
specific regional features and constraints. The study develops an economic and
mathematical model that considers both operational efficiency and cost
minimization by integrating different modes of transport such as road, rail,
and sea. Through a comprehensive analysis of existing literature and
application of advanced optimization algorithms, the study proposes a new
framework that improves the decision-making process in route planning and
carrier selection. The proposed model is validated with real-world examples,
demonstrating its practical applicability and potential to significantly improve
the efficiency of multimodal transportation systems under different scenarios.
Keywords: multimodal transportation chain, transport
systems, route optimization, carrier selection, shipping, holistic
approach, modes of transport, decision-making frameworks, containers,
transportation efficiency, cost minimization, logistics, optimization
algorithms
1. INTRODUCTION
The dynamic landscape
of multimodal transportation systems has led to numerous studies aimed at
optimizing various aspects of these systems, from route planning to the
integration of new technologies.
Integrated
optimization models are essential for improving carrier selection and route
planning in multimodal transport systems [1, 2]. These models take into account
various factors, including modes of transport, delivery windows and
cost-effectiveness, to ensure optimal operational efficiency. The dynamic
approach to studying the impact of delivery systems on infrastructure projects
highlights the need for adaptive strategies in multimodal transport [3, 4].
Integrated system solutions are crucial not only for addressing logistical
issues related to human factors, but also for improving efficiency through
innovative, science-based approaches [5, 6].
Technological
advances play a key role in optimizing delivery systems, such as the
integration of trucks and drones, which increases the efficiency of last-mile
delivery [7]. Optimizing production and transportation planning with a focus on
prefabricated components and time windows further demonstrates how proper
planning can lead to successful deliveries [8]. Neural network-based route
selection models have also proven to be effective, especially during global
disruptions, improving multimodal freight transportation systems [9]. The
selection of optimal routes and modes of transport under conditions of
uncertainty highlights the need for mathematical models to support
decision-making in logistics [10, 11].
Multimodal transport
routes can be further optimized using AND/OR graphs and discrete ant colony
optimization, as these methods have been shown to improve both risk management
and energy efficiency [12]. Genetic algorithms are widely used for
multi-objective transport route planning, providing computational advantages
that improve overall system performance [13]. The optimization approach for
periodic multimodal transport routes takes into account the need for regularity
and reliability of logistics operations [14]. In addition, the integration of
key processes in work areas into route planning is crucial to maintaining
efficiency and profitability [15].
A two-stage route
optimization algorithm for multimodal networks offers further insight into
improving transport efficiency [16]. Structural optimization of multimodal
freight delivery routes demonstrates the potential to improve freight transport
operational results [17]. Methodologies focused on consolidating cargo delivery
provide a basis for improving overall efficiency by optimizing the use of
available resources [18]. Digital delivery safety and efficiency management
systems are increasingly being implemented in multimodal transport systems,
helping to optimize safety and logistics operations [19].
In maritime
transport, ensuring the reliable and safe operation of technical systems is a
vital aspect of multimodal transport systems, especially with the integration
of energy-efficient engines [20]. The interaction between rolling stock and
infrastructure must be carefully managed to ensure the smooth operation of
transport systems, as shown in studies of their dynamic characteristics [21].
Leadership in transport organizations, especially with regard to preventive
maintenance, plays a key role in ensuring the safe and efficient operation of
transport systems [22].
The role of
cybersecurity in multimodal transport, especially in maritime systems, is
becoming increasingly important. Risk analysis models for maritime
cybersecurity emphasize the need to create secure systems to prevent potential
threats [23]. Comprehensive assessments of the maritime cybersecurity landscape
also provide insight into current challenges and opportunities for improving
security [24]. Education and training in multimodal transport systems is
important, especially in light of advances in autonomous shipping technologies,
where special programmes are needed to meet the needs
of the industry [25].
Energy-efficient
growth in ports plays an important role in multimodal transport systems, as
shown by studies focusing on the quality of port infrastructure and
superstructure [26]. Port efficiency is also affected by the quality of
infrastructure, which has a direct impact on logistics costs [27]. Future
opportunities for the development of port cities also demonstrate the prospects
for improving multimodal transport systems [28]. Blockchain
technology, which is still evolving, has the potential to increase transparency
and operational efficiency in maritime transport [29].
The optimization of
maritime cargo delivery continues to evolve through the use of genetic
algorithms [30], which have proven effective in improving route planning and
carrier selection [31]. Simulation modelling techniques and improved transport
route optimization further contribute to the efficiency of multimodal transport
operations [32]. The integration of real-time data and the professionalization
of transport operations offer further improvements in transport system
management [33, 34]. Multimodal transport systems also benefit from integrated
public transport and car sharing, which demonstrates the potential for more
sustainable and efficient transport systems [35]. Optimizing international
multimodal routes under conditions of uncertainty adds complexity, but
mathematical models provide reliable solutions for managing unpredictability in
logistics operations [36].
Competition in
seaports and its impact on technical efficiency is another key area, as shown
in studies analyzing European container ports [37]. Operational research in
road transport logistics also contributes to the development of more efficient
systems by optimizing route selection and carrier performance [38]. Genetic
algorithms remain the main tool for improving transport route planning [39],
and their continuous improvement continues to increase the efficiency of
multimodal transport networks [40]. A bibliometric analysis of maritime
transport trends highlights the importance of sustainable practices in
multimodal transport systems [41], and research on uncertainty theory
contributes to the further improvement of route optimization models for international
transport [42]. Finally, the integration of sustainability and operational
research continues to drive progress in the optimization of multimodal
transport systems, offering practical solutions to today's logistics challenges
[43].
The idea of an
integrated consideration of delivery systems was considered in the above
sources, where, in particular, a model was proposed that takes into account the
"economies of scale" and the formation of a synergistic effect for
the organizer of delivery systems (freight forwarding company). A continuation
of this approach was the work where a project-oriented approach to cargo
transportation orders within the project management office provided for an
integrated consideration of a set of operations related to cargo transportation
to ensure an increase in the volume of work to reduce their cost for the
freight forwarding company. The corresponding economic and mathematical model
is aimed at maximizing the synergistic effect to reduce the cost of
transportation services. It should be noted that the model focuses on the set
of operations of the transport and technological process, both basic and
additional.
Despite significant
advances in the optimization of multimodal transport systems, existing
approaches often consider individual components in isolation, resulting in
suboptimal solutions that fail fully to integrate carrier selection, route
planning, and synergistic economies of scale. This fragmentation limits the
potential for efficiency improvement and cost reduction, especially in the face
of uncertainty and complex operational constraints. Thus, the research problem
is to develop an integrated optimization model that integrates these aspects
into a holistic framework, improving operational efficiency and minimizing
costs by accounting for interdependencies, risk management, and real-world
complexities in multimodal transportation networks.
2. MATERIALS AND METHODS
The
development of ideas, taking into account the additional conditions inherent in
multimodal transportation and the multimodal transportation model developed for
the localized approach, allows us to formulate the following economic and
mathematical model.
Let
us consider a multimodal transportation system within a certain period of time 
,
each of which is characterized by the following set of characteristics:
(1)
where Qm –
is the number of containers (TEU) with cargo to be
transported from the point of gm
to the point hm,
these points belong to the set of points (nodes) of the transport network 
, 
– accordingly, a time limit and a possible
increase in this time limit.
Let
us consider 
– control parameter, the
essence of which is the choice for the order m a particular carrier l of a certain type of transportation
k for transportation by communication ij,
the choice of a particular carrier corresponds to the value
.
It
should be noted that the choice of carriers for the maritime component is not
made from the set of all carriers operating in this direction of transportation
(communication), but from the set of 
those whose schedule meets the requirements
for departure times as previously established.
The
objective function meets the optimality criterion, which is proposed to use the
total costs of a multimodal operator, taking into account possible risks for
the entire multimodal transportation system under consideration:
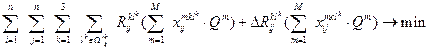(2)
This
expression (2) takes into account the entire path of the cargo system,
considering all modes of transport and carriers. The objective function also
takes into account the dependence of the cost of transportation 
for each communication and each carrier of the
total amount of cargo (TEU) Q.
Considering
the need to meet transportation deadlines, the following restriction takes into
account the total time for each multimodal transportation:
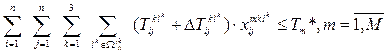(3)
where 
– the maximum permissible
period of multimodal transportation, which is determined by the cargo owner for
each order 
. If
the "area of compromise" approach is followed, as it was before, this
limitation can be adjusted:
(4)
where 
– permissible increase of the
specified period of multimodal transportation according to the conditions of
the cargo owner.
Next,
we consider two groups of constraints that ensure the formation of a scheme in
which, if necessary, the sections are sequenced for each order – multimodal transportation 
.
The
first group of model constraints takes into account the need for cargo to
"exit" each intermediate point – the nodes of the transportation
network:
i.e.
for all points that are intermediate for each multimodal transportation, the
number of "inbound" and "outbound" communications is the
same (whether they are selected or not).
It
should be noted that this model is focused on a network of any type in terms of
transport links, so the constraint expressions take into account any
"detour" of transport nodes from the first (departure) to the last
(destination) for each transportation.
The
second group of constraints reflects the specifics of the first and last points
for each order, i.e. the cargo must leave the first point and enter the last
(destination):
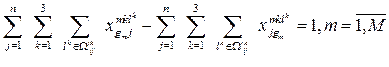(6)
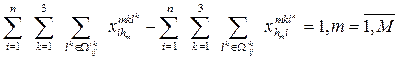(7)
this
establishes that the number of "outgoing" and the number of
"incoming" communications from and to the points of departure and
destination, respectively, should be one more.
The
condition of the values of the model control parameters (variables):
(8)
The
expressions (2)-(8) form an economic and mathematical model for determining the
optimal schemes and composition of carriers for the multimodal transportation
system when they are considered in an integrated manner.
It
should be noted that the proposed model considers the formation schemes for each
multimodal transportation separately, but the costs, taking into account the
risks of their increase, are considered in total, taking into account the dependencies 
.
Let
us consider the following example with a 4-modal transportation system 
by volume 
,
with time limits 
and a possible increase in transportation time
,
considered on the transportation network shown in Fig. 1. It should be noted that, unlike the previous
example, when a single multimodal transportation was considered, the transport network
assumes bilateral communications, i.e., from each point to those with which
there is a transport connection, it is possible to reach in one direction and
in the other, taking into account the need for experimental verification of
"multidirectional" shipments within the system under consideration.
It
should also be added that the presence of "return" cargo is one of
the sources of synergy for a multimodal operator, as carriers are inclined to
make price concessions for the opposite direction, especially when it comes to
cargo in containers, where there is always an imbalance between exports and
imports.
3. RESULTS AND
DISCUSSION
Thus,
carriers working on communication A12, also work in communication A21.
Therefore, Table 1 shows the characteristics for only one direction of
communication, given that the composition of carriers in the opposite direction
is the same.
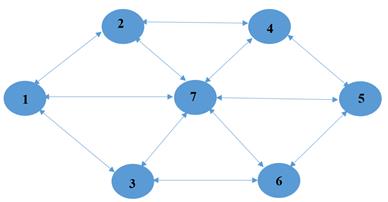
Fig. 1. Scheme of transport communications for the design example
Tab. 1
Possible alternatives for transport communications
|
Communication |
Type of transportation |
Transportation companies |
|
A12 |
k=1,2 |
l1=1,2 l2=1 |
|
A13 |
k=1 |
l1=1,2 |
|
k=3 |
l3=1,2 |
|
|
A27 |
k=3 |
l3=1,2 |
|
A24 |
k=3 |
l3=1,2,3 |
|
A37 |
k=3 |
l3=1,2 |
|
A36 |
k=3 |
l3=1,2 |
|
A47 |
k=3 |
l3=1,2 |
|
A45 |
k=3 |
l3=1,2 |
|
A65 |
k=3 |
l3=1,2 |
|
A67 |
k=3 |
l3=1,2 |
|
A75 |
k=3 |
l3=1,2 |
The
characteristics of transportation for alternative carriers by different modes
of transport are shown in Tables 2 and 3. It should be noted that in this case,
transportation costs and risks are taken as dependencies on the volume of the
container batch (TEU). We assume risks as a
percentage of the transportation cost. Also, for this example, it is assumed
that the costs in the opposite direction are the same, but in practice, as a
rule, transportation rates in the import/export directions differ. This
assumption does not affect the experimental validation of the model, as it only
reduces the amount of input data.
Tab. 2
The characteristics of transportation costs for alternative carriers by
different modes of transport
|
Communication |
Type of transportation |
Transportation companies |
|
|
|
|
k=1 |
l1=1 |
|
10 |
|
l1=2 |
|
5 |
||
|
k=2 |
l2=1 |
|
7 |
|
|
|
k=1 |
l1=1 |
|
10 |
|
l1=2 |
|
3 |
||
|
|
k=3 |
l3=1 |
|
7 |
|
l3=2 |
|
7 |
||
|
|
k=3 |
l3=1 |
|
10 |
|
l3=2 |
|
12 |
||
|
|
k=3 |
l3=1 |
|
10 |
|
l3=2 |
|
8 |
||
|
l3=3 |
|
5 |
||
|
|
k=3 |
l3=1 |
|
7 |
|
l3=2 |
|
5 |
||
|
|
k=3 |
l3=1 |
|
5 |
|
l3=2 |
|
10 |
||
|
|
k=3 |
l3=1 |
|
8 |
|
l3=2 |
|
5 |
||
|
|
k=3 |
l3=1 |
|
7 |
|
l3=2 |
|
5 |
||
|
|
k=3 |
l3=1 |
|
5 |
|
l3=2 |
|
3 |
||
|
|
k=3 |
l3=1 |
|
3 |
|
l3=2 |
|
10 |
||
|
|
k=3 |
l3=1 |
|
8 |
|
l3=2 |
|
5 |
Tab. 3
The characteristics of transportation time and its possible deviation
for alternative carriers by different types of transport
|
Communication |
Type of transportation |
Transportation companies |
|
|
|
|
k=1 |
l1=1 |
5 |
0,5 |
|
l1=2 |
5 |
0,5 |
||
|
k=2 |
l2=1 |
8 |
1 |
|
|
|
k=1 |
l1=1 |
5 |
0,5 |
|
l1=2 |
5 |
1 |
||
|
|
k=3 |
l3=1 |
20 |
0,5 |
|
l3=2 |
22 |
1 |
||
|
|
k=3 |
l3=1 |
18 |
1 |
|
l3=2 |
17 |
1 |
||
|
|
k=3 |
l3=1 |
18 |
2 |
|
l3=2 |
16 |
1 |
||
|
l3=3 |
16 |
0,5 |
||
|
|
k=3 |
l3=1 |
17 |
1 |
|
l3=2 |
20 |
1 |
||
|
|
k=3 |
l3=1 |
10 |
1 |
|
l3=2 |
11 |
2 |
||
|
|
k=3 |
l3=1 |
18 |
1 |
|
l3=2 |
17 |
1 |
||
|
|
k=3 |
l3=1 |
18 |
2 |
|
l3=2 |
16 |
1 |
||
|
|
k=3 |
l3=1 |
17 |
1 |
|
l3=2 |
20 |
1,5 |
||
|
|
k=3 |
l3=1 |
10 |
1 |
|
l3=2 |
11 |
1 |
||
|
|
k=3 |
l3=1 |
10 |
1 |
|
l3=2 |
11 |
0,5 |
The
initial data on the volume of batches of transportation orders and time
constraints are as follows:
(TEU),
(days),
(days).
A
graphical representation of certain cost dependencies on the volume of
transportation (number of containers) is shown in Fig. 2. It should be noted
that, in practice, the dependencies do not have such a "perfect"
form; however, this does not affect the reliability of the results, as the
primary objective is to identify a correlation between cost and the number of
containers.
It
should be noted that, based on the initial data on the transport network and
alternative carriers, the model provides 200 control parameters (variables)
that reflect alternatives for transportation on separate communications in both
directions. For the given initial data, the first stage of the study obtained
the following optimal schemes and composition of carriers (Fig. 3-5).
The
time of multimodal transportation was respectively: 
(days).
Further,
the conditions for time limits have been changed, taking into account
(days).
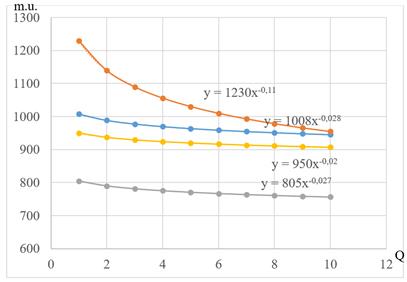
Fig. 2. Graphical interpretation of certain dependencies of
transportation costs on the volume of the container batch
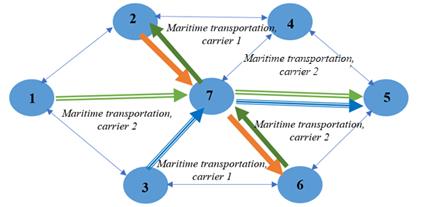
Fig. 3. Optimal schemes and composition of carriers for the baseline
scenario
Reducing
the allowable time for multimodal transportation led to changes in carriers on
certain sections of the schemes (Figures 4-6), and, as a result, to an increase
in the value of the objective function from 7066 to 8446 m.u.
(monetary units, i.e., total costs). But this ensured that the transportation
time conditions were met. For the given time conditions, the schemes, and
composition of carriers provide: (days).
In
this case, the time for the third order increases, but for the second order,
the transportation time decreases from 34.5 days to 32 days. Thus, the
multimodal operator can offer the shipper of the second order to accept the
transportation time of 34.5 days, but at a lower cost, given that the total
costs for the first option are significantly lower.
Thus,
the average cost of multimodal transportation of one container with cargo under
the first option is 7066/12=588.83 m.u., under the
second option 8446/12=703.85 m.u. (12 TEU – the total number of containers with cargo in 4
orders), so the operator has the economic opportunity to offer a reduction in
the cost of multimodal transportation for the customer if he agrees with the
proposed transportation time.
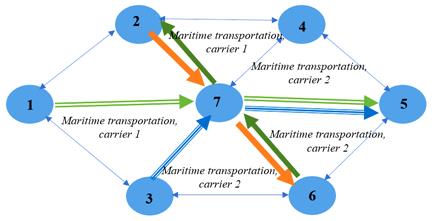
Fig. 4. Optimal schemes and composition of carriers to reduce
the acceptable time of multimodal transportation
Further,
in the course of the experimental study, a situation was assumed when one of
the nodes – in this case, the "hub" – node 7 – was not operational;
the current state of multimodal transportation demonstrates the practical
possibility of such situations. This causes a change in the optimal schemes, as
shown in Fig. 5, where Fig. 6 depicts the implementation of this optimization.
Further,
for the given conditions, we considered different options for the volume of
container batches for each order – one unit more and one unit less than for the
initial option, i.e., the total number of 8, 12 and 16 TEU.
Increasing the batch size logically led to a decrease in the average cost of
transportation of one container in monetary units (m.u.),
(Fig. 6).
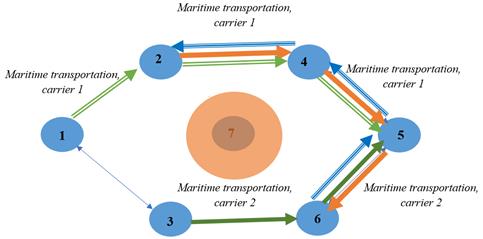
Fig. 5. Optimal schemes and composition of carriers when node 7 is
excluded
Thus,
experimental calculations have demonstrated how the proposed model is used as a
tool for implementing the agile approach within the trade-off domain. Changes
in the initial data are reflected in the change in the optimal values of the
control parameters and the value of the objective function, which substantiates
the reliability of the proposed models.
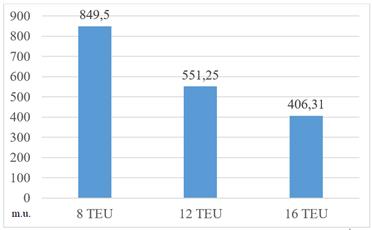
Fig. 6. Changes in the average cost of multimodal transportation
per TEU for different total order volumes, m.u.
The
special attention should be paid to the formation of a synergistic effect,
based on the economies of scale that are formed when increasing the number of
containers passing through the same communications using certain carriers,
including in the opposite direction. Experimental studies have demonstrated the
formation of this effect and its corresponding reflection in the optimization
results.
Earlier,
the mathematical expression for the synergistic effect was given in a general,
more conceptual form. Taking into account the results obtained in this section,
the expression for the synergistic effect can be presented as follows:
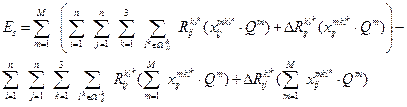(9)
where
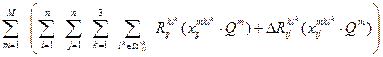(10)
– are the total
costs for a multimodal transportation system without taking into account the
possibilities of their integration, i.e.
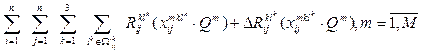(11)
characterizes the
costs of each individual multimodal transportation when considered locally.
It
should be noted that the synergistic effect proposed in [7] was considered as
an optimization criterion, and its maximization ensured the maximum profit of
the freight forwarding company. In our opinion, the use of such a criterion is
interesting from the point of view of the theoretical solution of the problem
under consideration, but complicates the task in practical implementation.
Since it is necessary to find and evaluate the optimal schemes and composition
of carriers for each multimodal transportation (local level)). Despite the fact
that modern information technology allows this to be done quickly, there is a
question of whether it is feasible in practice. However, if such a need arises,
the results presented in this section allow us to do so.
Thus,
a model has been developed to determine the schemes (routes) and the
composition of carriers for the multimodal transportation system of a
multimodal operator. Varying the chains of the corresponding system –
intermediate points, modes of transport and carriers – causes variation in the
main characteristics of each multimodal transportation, as well as the total
costs of the operator in the implementation of these transportations. The model
takes into account the possibility of reloading vehicles, the use of a tariff
system based on the dependence of the cost of transportation and the
performance of individual transportation operations on the volume of the
consignment (number of containers with cargo).
This results in a synergistic effect that improves the efficiency of
multimodal transportation for both the multimodal operator and cargo owners,
providing them with a wider range of options in the area of compromise.
4. CONCLUSION
The model proposed in this article
belongs to the class of nonlinear models (the objective function takes into
account the nonlinear dependence of costs on the number of containers) and is
based on the existing model of integral optimization of containerized cargo
deliveries, but the development of this result is to take into account the
specifics of multimodal transportation from the point of view of the operator.
The model considers the operator's risks for each alternative option in the system,
as well as its reliability. The synergistic effect that is formed when
considering the multimodal transportation system in an integrated manner is
formalized, based on the economies of scale that are formed when increasing the
number of containers that pass through the same communications using certain
carriers, including in the opposite direction. Relevant experimental studies
have been carried out to substantiate the reliability of the optimization
results based on the proposed model.
References
1.
Lasota M, A.
Zabielska, M. Jacyna, P. Gołębiowski, R. Żochowska, M. Wasiak. 2024. "Method for Delivery
Planning in Urban Areas With Environmental
Aspects." Sustainability 16(4):
1571. DOI: 10.3390/su16041571.
2.
Peng
Y., Z. Mo, S. Liu. 2021. "Passenger’s Routes Planning in Stochastic
Common-Lines’ Multi-Modal Transportation Network Through
Integrating Genetic Algorithm and Monte Carlo Simulation." Archives of Transport 59(3): 73-92. DOI: 10.5604/01.3001.0015.0123.
3.
Meshref N., A. Elkasaby, O. Wageh. 2024. "Dynamic Approach for Investigating
Delivery System Effects On Infrastructure Project
Performance." Engineering Construction & Architectural Management.
DOI: 10.1108/ECAM-10-2022-1022.
4.
Zhang,
J., H. Li, W. Han, Y. Li. 2024. "Research on Optimization of
Multimodal Hub-And-Spoke Transport Network Under Uncertain Demand." Archives of Transport 70(2): 137-157. DOI: 10.61089/aot2024.1g17bx18.
5.
Gear
C. 2024. "Integrated System Responses for Families Impacted by Violence: A
Scoping Review." International Journal of Integrated Care 27. DOI: 10.5334/ijic.7542.
6.
Pepler E., L. Kinsman. 2024. "The Call for an
Evidence-Based Integrated Funding and Service Delivery System for
Newcomers." Healthcare Management Forum 8404704241267243. DOI: 10.1177/08404704241267243.
7.
Zhang
J., J. Campbell, D. Sweeney II. 2024. "A Continuous Approximation Approach
to Integrated Truck and Drone Delivery Systems." Omega 126. DOI: 10.1016/j.omega.2024.103067.
8.
Dan
Y., G. Liu. 2023. "Integrated Scheduling Optimization of Production and
Transportation for Precast Component with Delivery Time Window." Engineering
Construction and Architectural Management 31. DOI:
10.1108/ECAM-09-2022-0871.
9.
Kayikci Y., E. Cesur. 2023.
"Artificial Neural Networks-Based Route Selection Model for Multimodal
Freight Transport Network During Global
Pandemic." Academic Platform Journal of Engineering and Smart Systems
11. DOI: 10.21541/apjess.1294957.
10. Jacyna M., Semenov I. 2020. "Models
of vehicle service system supply under information uncertainty. " Eksploatacja i Niezawodnosc - Maintenance and
Reliability 22(4): 694-704. DOI: 10.17531/ein.2020.4.13.
11. Li L., Q. Zhang, T. Zhang, Y. Zou, X.
Zhao. 2023. "Optimum
Route and Transport Mode Selection of Multimodal Transport with Time Window
Under Uncertain Conditions." Mathematics 11. DOI:
10.3390/math11143244.
12. Wang Z., M. Zhang, R. Chu, L. Zhao. 2020. "Modeling and Planning
Multimodal Transport Paths for Risk and Energy Efficiency Using AND/OR Graphs
and Discrete Ant Colony Optimization." IEEE Access. DOI: 10.1109/ACCESS.2020.3010376.
13. Kang F., X. Li, J. Li. 2021. "Analysis of Multi-Objective
Multimodal Transport Route Planning Based on Genetic Algorithm." Application
of Intelligent Systems in Multi-Modal Information Analytics. DOI: 10.1007/978-3-030-74811-1_5.
14. Dini N., S. Yaghoubi,
H. Bahrami. 2024. "Route Selection of Periodic
Multimodal Transport for Logistics Company: An Optimisation
Approach." Research in Transportation Business & Management
54. DOI: 10.1016/j.rtbm.2024.101123.
15. Wang Y., R. Song, Z. Zhao, R. Zhao, Z.
Zhang. 2024. "A
Multimodal Material Route Planning Problem Considering Key Processes at Work
Zones." PLOS ONE 19. DOI: 10.1371/journal.pone.0300036.
16. Qiao C., K. Niu, W. Ma.
2024. "Multimodal
Network Path Optimization Based on a Two‐Stage Algorithm in the Perspective of Sustainable Transport
Development." Advanced Control for Applications: Engineering and
Industrial Systems. DOI: 10.1002/adc2.187.
17. Taran I., R. Olzhabayeva, M. Oliskevych,
V. Danchuk. 2023.
"Structural Optimization of Multimodal Routes for Cargo Delivery." Archives
of Transport 67: 49-70. DOI:
10.5604/01.3001.0053.7076.
18. Smrkovska V.Yu.
2008. "Methodological Foundations of Organizing Cargo Delivery Using
Consolidation Tools." PhD Thesis,
Odessa National Maritime University, Odesa.
19. Larbi J., L. Tang, R. Larbi,
D. Abankwa, R. Danquah.
2024. "Developing an Integrated Digital Delivery Framework and Workflow
Guideline for Construction Safety Management in a Project Delivery System."
Safety Science 175. DOI: 10.1016/j.ssci.2024.106486.
20. Sagin S., V. Madey,
A. Sagin, T. Stoliaryk, O. Fomin, P. Kučera. 2022.
"Ensuring Reliable and Safe Operation of Trunk Diesel Engines of Marine
Transport Vessels." Journal of Marine Science and Engineering
10(10): art. no. 1373. DOI:
10.3390/jmse10101373.
21. Fomin O., P. Prokopenko,
D. Turovets, A. Fomina.
2022. "Interaction Assessment of the Component Parts of the Rolling Stock
with the Infrastructure by Determining the Dynamic Characteristics of the Movement
of Converted Hopper Wagons After Long-Term Operation." Transport Means
- Proceedings of the International Conference 2022-October: 870-875.
22. Choo A., Y. Xia, G. Peter Zhang, C.
Liao. 2024. "Leader Behavioral Integrity for Safety and Its Impact on Worker
Preventive Maintenance Behavior and Operational Performance." Safety
Science 177: art. no. 106577. DOI:
10.1016/j.ssci.2024.106577.
23. Tatar U., B. Karabacak,
O.F. Keskin, D.P. Foti. 2024. "Charting New Waters with CRAMMTS: A Survey-Driven Cybersecurity Risk Analysis Method
for Maritime Stakeholders." Computers and Security 145: art. no. 104015. DOI: 10.1016/j.cose.2024.104015.
24. Dimakopoulou A., K. Rantos.
2024. "Comprehensive Analysis of Maritime Cybersecurity Landscape Based on
the NIST CSF v2.0." Journal
of Marine Science and Engineering 12(6): art. no.
919. DOI: 10.3390/jmse12060919.
25. Meštrović T., I. Pavić,
M. Maljković, A. Androjna.
2024. "Challenges for the Education and Training of Seafarers in the
Context of Autonomous Shipping: Bibliometric Analysis and Systematic Literature
Review." Applied Sciences 14(8): art. no.
3173. DOI: 10.3390/app14083173.
26. Nigro M., M. De Domenico, T. Murgia, A.
Stimilli. 2024.
"The Port Sector in Italy: Its Keystones for Energy-Efficient
Growth." Energies 17(7): art. no. 1788. DOI: 10.3390/en17071788.
27. Fitrianto A., M. Al Musadieq, E. Yulianto,
S. Worokinasih. 2024.
"Port Performance as a Mediation of the Influence of Infrastructure and
Superstructure Quality in Realizing Efficient and Effective Logistic Cost
Ports." Journal of Maritime Research 21(1): 157-162.
28. Zain R.M.,
J. Jeevan, N.H.M. Salleh,
A.H. Ngah, A. Ramli, M.Z.M. Zain, L.S. Yekini, A.N. Dirie.
2024. "Future Opportunities for Port City Development: A Reciprocal
Evaluation for Competitive Advantage for Malaysian Seaports." Journal
of Maritime Research 21(1): 265-282.
29. Bauk S., R. Mujalović, N. Kapidani, Z. Paladin. 2023. "Maritime Blockchain Prospects and Concerns." Journal of
Maritime Research 20(2): 97-105.
30. Romanuke V.V., A.Y.
Romanov, M.O. Malaksiano.
2022. "Pseudorandom Number Generator Influence on the Genetic Algorithm
Performance to Minimize Maritime Cargo Delivery Route Length." Pomorstvo 36(2): 249-262. DOI:
10.31217/p.36.2.9.
31. Romanuke V.V., A.Y.
Romanov, M.O. Malaksiano.
2022. "Crossover Operators in a Genetic Algorithm for Maritime Cargo
Delivery Optimization." Journal of Eta Maritime Science 10(4):
223-236. DOI: 10.4274/jems.2022.80958.
32. Romanuke V.V., A.Y.
Romanov, M.O. Malaksiano.
2023. "A Genetic Algorithm Improvement by Tour Constraint Violation
Penalty Discount for Maritime Cargo Delivery." System Research and
Information Technologies 2023(2): 104-126. DOI:
10.20535/SRIT.2308-8893.2023.2.08.
33. Melnyk O., S. Onyshchenko,
O. Onishchenko, Y. Koskina,
O. Lohinov, O. Veretennik,
O. Stukalenko. 2024. "Fundamental Concepts of
Deck Cargo Handling and Transportation Safety." European Transport - Trasporti Europei (98). DOI: 10.48295/ET.2024.98.1.
34. Melnyk O., S. Onyshchenko,
O. Onishchenko, O. Shcherbina,
N. Vasalatii. 2023. "Simulation-Based Method for
Predicting Changes in the Ship's Seaworthy Condition Under
Impact of Various Factors." Studies in Systems, Decision and Control
481: 653-664. DOI: 10.1007/978-3-031-35088-7_37.
35. Hulianytskyi L., O. Rybalchenko.
2023. "Route Optimization in Mission Planning for Hybrid DRONE+VEHICLE Transport Systems." Cybernetics and
Computer Technologies: 44-58. DOI:
10.34229/2707-451X.23.3.4.
36. Sijabat P., R. Wulandari, W. Kurniawan, M.
Agustinawati, M. Simanjuntak. 2024. "Enhancing Multimodal Route Optimization in Maritime
Transport: Integrating Real-Time Data and Professionalism." TEMATIK 11: 72-77. DOI:
10.38204/tematik.v11i1.1880.
37. Cherednichenko K., V. Ivannikova,
O. Sokolova, M. Yanchuk.
2023. "Model of Transport Safety Assessment in Multimodal Transportation
Systems." Transport 38: 204-213. DOI:
10.3846/transport.2023.20865.
38. Huang H., D. Bucher, J. Kissling, R.
Weibel, R. Martin Raubal. 2018. "Multimodal Route Planning With
Public Transport and Carpooling." IEEE Transactions on Intelligent
Transportation Systems: 1-13. DOI: 10.1109/TITS.2018.2876570.
39. Wang X., P. Zhang, Z. Du, A.-Q. Tian, H. Lv. 2024. "Research on Optimization of International Multimodal
Transportation Routes Based on Uncertainty Theory." Transportation
Research Record: Journal of the Transportation Research Board. DOI: 10.1177/03611981241242377.
40. Sosedová J., M. Jurkovič,
A.M. Baracková, J. Majerová,
P. Gorzelanczyk, O. Stopka.
2024. "Bibliometric Overview of Current Trends in Maritime Transport: The
Issue of a Special Interest in Delivery of a Consignment as a Tool to Achieve
Sustainability of International Transport." Communications - Scientific
Letters of the University of Žilina 26(1): A11-A21. DOI: 10.26552/com.C.2024.008.
41. Jurkovic M., T. Kalina, P. Gorzelanczyk,
M. Stopkova. 2023. "Use of Operational Research in Car
Transport Logistics." Lecture Notes in Networks and Systems 640 LNNS: 141-150. DOI:
10.1007/978-3-031-26655-3_13.
42. Kan E. 2024. "Identifying Company
Selection Criteria Applied by Maritime Transportation Engineering Students for
Career Planning." Transactions on Maritime Science 13(1). DOI: 10.7225/toms.v13.n01.w08.
43. Kammoun R., C. Abdennadher.
2023. "The Impact of Seaport Competition on Technical Efficiency: Simar-Wilson Analysis of European Container Ports." Transactions
on Maritime Science 12(2). DOI: 10.7225/toms.v12.n02.w06.
Received 03.08.2024; accepted in revised form 11.10.2024
Scientific
Journal of Silesian University of Technology. Series Transport is licensed
under a Creative Commons Attribution 4.0 International License