Article citation information:

Mańka, A. Problems and good practices of measuring the railway wheel rolling diameter. Scientific Journal of Silesian University of Technology. Series Transport. 2024, 125, 167-176. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2024.125.11.

Adam MAŃKA[1]

PROBLEMS AND GOOD PRACTICES OF MEASURING
THE RAILWAY WHEEL ROLLING DIAMETER

Summary. The article describes the results of research on the influence of the methods used to measure the rolling diameter of a railway wheel "D" and measuring instruments on the accuracy of the obtained results. The differences in the results obtained using five different measuring instruments are presented. In particular, the difficulty of meeting the repair criterion |D-D'| was pointed out using the current measurement method. The article also illustrates the original measurement method proposed by author, which is a reference measurement for currently used methods, along with its limitations.

Keywords: railway wheel, wheelset, diameter of railway wheel, diameter difference, parameter |D-D'|, diameter measurement method, new measurement method

1. INTRODUCTION

To enable the operation of railway vehicles, it is necessary to ensure their required technical condition. As part of periodic tests of the technical condition of the vehicle, measurements are taken of those values that indicate the state of wear of elements that are important for the technical safety of the vehicles. Taking measurements and comparing them with the limit values contained in the maintenance manual system (MMS) allows for an unambiguous engineering assessment of the vehicle's condition and the approval or withdrawal of the vehicle from operation. The railway wheel set, as an element particularly responsible for safety, is subject to a rigorous maintenance process. This process is described in detail in each documentation of the MMS of railway vehicles and includes a measurement card. An important element of this measurement card is the indication of the values that are to be measured together with the provision of reference values, which are the basis for the engineer to make decisions on the further operation of this element. Reference values, like other elements of the MMS, are indicated as mandatory in [1 - (§13.2 c)], i.e.: design values, post-repair values and limit values.

2. ANALYSIS OF NORMATIVE REQUIREMENTS IN TERMS OF THE |D-D’| CRITERION

Requirements concerning the method of measurement, maintenance process, measured values and reference values are also the subject of Journals of Laws, Railway Instructions, standards and Technical Specifications for Interoperability (TSI) among others in publications [2÷12]. Currently, a significant part of the above-mentioned documents is not obligatory due to the lack of reference in higher-level legal acts (act, directive, regulation, including TSI, announcement). This leaves ECM (Entity in Charge of Maintenance) units without superior guidelines and the need to rely on good industry practices. It is important to emphasize the fact that each new edition of TSI, standards or other industry requirements may introduce the standards indicated below and then the provisions contained therein become mandatory. This is another premise for constant monitoring of railway regulations in the field of vehicle maintenance, introducing changes and continuous improvement of MMS.

For the analysis of the requirements of the selected value |D-D’| characterizing the railway wheel set, 12 normative and legal sources [1÷12] were taken into account. Considering the maintenance process, the analysis of legal requirements was started with the regulation [1]. This regulation is a current mandatory legal act, but it does not define precise requirements or values in the scope of the parameter |D-D’|. The analysed TSI Loc&Pas [2] is a current and mandatory document. TSI Loc&Pas [2] does not state this criterion directly but indicates the need to maintain compliance with EN14363 standards and to apply EN 13979-1:2003+A2:2011 standards, however, within the scope of points 7.2.1, 7.2.2, 7.2.3 and 7.3 and 6 of this standard. TSI Loc&Pas also refers to EN 13260:2009 +A1:2010 (3.2.1). It should be noted that this standard has already been updated, but due to the indication of a specific edition in the TSI, it is still legally required. TSI [2] itself in Tables 1 and 2 contains requirements for SR, Sd, Sh and qr, but without |D-D’|. From the standards listed in the TSI, the EN 14363+A2:2023-01 [3] and 13979-1:2020-12 [4] standards are up to date, but they do not directly define the values of the post-repair geometric parameters of the railway wheel. It is important that the TSI [2] refers to the EN 13260:2021-02 [5] standard as mandatory, but only indicates its point 3.2.1, which means that although this standard precisely defines the geometric parameters of railway wheels, including |D-D’| £0.3 mm and £0.5 mm, depending on the speed of movement for V £120 km/h and over 200 km/h, respectively, these elements are not mandatory, but only the elements included in point 3.2.1 of the publication [5]. EN 15313 [6] is current and defines the parameter |D-D’|, similarly to the above 0.3 and 0.5 mm for V£120 km/h and V>120 km/h, respectively, but as a value after reprofiling and not as a decision criterion for reprofiling.

EN 13715 [7] was also analysed due to the subject of the standard "Running surface outline" included even in the title. This standard is current, but it also does not indicate the repair values of the measured geometric parameters of the wheel outline. The railway standard PN-92/K-91056 [8], which is the prototype of the above standard, also does not include permissible values for the geometric dimensions of the wheel. The same applies to EN 15302 [8] and EN 14363 [10] as well as EN 17095 [11].

Only the PN-K-91045 [12] standard from 2002 defines the outline of wheel sets and the parameters |D-D’| < 0.5 mm, however, this standard has been withdrawn from use. It is also worth noting that this standard required a value below, but not equal to 0.5 mm (important symbol) for all vehicles with an operating speed V below 200 km/h. It can therefore be seen that the currently selected standards indicate permissible values, but these requirements are not mandatory. Therefore, when verifying the railway instructions of several carriers, a significant discrepancy can be seen in the scope of this criterion, i.e. |D-D’| from £ 0.3 mm through < 0.5 mm to £ 1 mm. This is not a favourable situation both from the point of view of the safety of the railway system and the arguments for the values adopted by individual railway entities in the DSU. This situation is also not conducive to the development of uniform requirements for the maintenance of rail vehicles, which at the current stage of railway development in the EU is becoming an expected and justified element from the point of view of economics and ensuring safety.

3. ACCURACY OF MEASUREMENTS OF PARAMETERS DESCRIBING A RAILWAY WHEEL SET AND WHEEL PROFILE

The most important parameters that constitute the basis for determining the technical condition of railway wheel sets include: qr, Az (AR), Ez (SR), Ow (Sh), Og (Sd), b (BR) and D and |D-D’|. Based on current measurement experience and control, measurement and research equipment used in the industry, these parameters are measured with the following accuracies (measurement uncertainty / resolution):

• qr, rim steepness, (1 mm / 1 mm);

• AR, distance between the inner surfaces of the rims or wheel rims in wheel sets without load (1 mm / 1 mm);

• SR, guide width (indirect measurement based on AR);

• Sh [h], rim height, (0.1 mm / 0.1÷0.01 mm);

• Sd [e], rim thickness, (0.1 mm / 0.1÷0.01 mm);

• BR, rim width, (0.1÷0.05 mm / 0.1÷0.05 mm);

• D [d], rolling circle diameter, (0.1÷0.2 (0.08*) mm/0.1÷0.01 mm);

• |D-D’|, difference in rolling diameter of a wheel for one wheel set, (indirect measurement based on D);

• |Dmax-Dmin| difference in wheel diameters between drive and rolling bogie sets, between drive bogie sets, between rolling bogie sets, between rolling and driving bogie sets, (indirect measurement based on D).

It can therefore be seen that the measurement of the wheel rolling diameter D mm, and even more so the differences |D-D’| and the series |Dmax-Dmin| determined multiple times on this basis, are burdened with measurement uncertainty, which is of significant importance for maintaining the decision criterion.

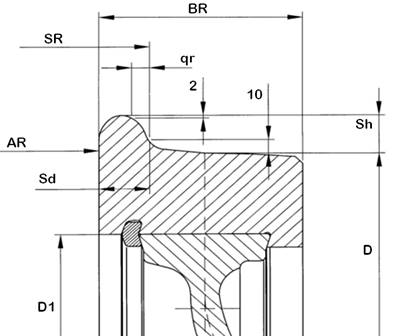
Fig. 1. Designations of the wheel rolling profile elements, wheel cross-section and
wheel set geometry [13, 14]

4. RESEARCH METHODOLOGY

To identify possible problems and differences in the measurement of the |D-D’| parameter, a series of measurements of the rolling diameter of the railway wheel D were performed using several measuring devices, including:

• 3 devices – three-point diameter gauges of various types and manufacturers;

• 1 optical device;

• 1 vernier calliper with a range of 1000 mm and accuracy of ±0.02 mm equipped with designed and manufactured measurement bases (designation in the study SN).

To verify measurement errors, a single, untied wheel of the 22WE type vehicle made of ER8 material and a nominal diameter of 850 mm was tested. The wheel was measured dismantled from the wheel set in the repair hall. The nominal diameter of the new wheel of the tested type is 850 mm. The tested wheel comes from a vehicle designed to travel at a maximum speed of 160 km/h. Before measurements, the wheel was cleaned of oxides and degreased with CX80. One section was left raw for further verification of the effect of cleaning on measurement accuracy.

5. THE COURSE OF THE RESEARCH AND THE OBTAINED RESULTS

The AA type measuring device (AA, BB, CC - authors' designations) was used to perform 95 measurements of the same railway wheel. The manufacturer of the AA device declares measurement accuracy of ±0.1 mm and resolution of 0.1 mm or 0.01 mm.

The first series of measurements (34 measurements) was performed within 5 minutes of the device being delivered to the hall, which did not guarantee that the temperature of the measuring device would be established. The measurements were performed in November at an outside temperature of approx. 10⁰C and an inside temperature of approx. 19⁰C. The results obtained unequivocally confirmed the significance of the manufacturer's recommendation that to obtain correct measurement results, the measurement should be performed only after the temperature of the device has been established and taking into account the recommendations to hold the device in designated places (heating at the temperature measurement points).

The average (maximum) value of the differences in the measured parameter D for a single point was:

• for the first series of measurements: 0.47 mm (0.7 mm);

• for the second series of measurements: 0.13 mm (0.3 mm).

Based on the measurements performed, it is therefore clear that failure to consider the need to establish and equalize the temperature of the device with the temperature of the measured object may result in obtaining an average difference value D more than 3.6 times greater than in the steady-state conditions. Therefore, only the second measurement series and measurements with other devices performed after the temperature had stabilized are considered for further tests. Analysing the detailed measurement results presented in Fig. 2, it can be stated that the average value of the wheel diameter was D_meanAA=797.47 mm with a spread between the maximum and minimum value of as much as dD_AA=1.6 mm. Significant differences in the measurement values between individual points may indicate ovalisation of the wheel or imperfections of the measurement method for the three-point method.

Significant differences in the measurement values were also obtained between the left, right and center / point sides. This is obtained for all points, i.e. A, B and C: dD_A=1.3 mm; dD_C=1.2 mm; dD_D=1.6 mm. It can be seen that changing the position of the measuring point by only about ±120 mm around the circumference of the wheel (which is described as the left or right side) results in a measurement result that differs by as much as 1.6 mm (with very good repeatability in a single point). This indicates that the measuring device indicates repeatable results, while the place of application of the measuring base on the wheel or its rolling diameter shows significant deviations from the average value. Such a significant dispersion of results depending on the measurement location makes it difficult to make a clear decision on meeting the requirements in terms of the |D-D’| or |D_max-D_min| criterion. i.e. both in the range of <0.5 mm after turning (repair dimension)), requirements indicated in the MMS for the vehicle (limit dimension |D-D’| <1 mm. Having the above measurement results available and the unambiguous confirmation of very good repeatability of measurement results at one point, proving the quality of the measuring device, it was necessary to analyse whether the cause of these discrepancies is not caused by wheel ovality or unevenness on its rolling surface. For this purpose, a parametric model of the measuring system was introduced (Fig. 2), for which the influence of unevenness at the point of contact between the measuring head and the wheel on the obtained rolling diameter of the wheel D was simulated.

In Fig. 3, the red arrows represent two measurement bases, and the green colour represents the measurement location with the measuring head (micrometre sensor) of the three-point inside diameter gauge. The results obtained based on this simulation clearly show that even the smallest local defects of the wheel cause very large, often unacceptable changes in the measurement result. This means that the measurement performed using this method depends on local defects on the railway wheel surface. To minimize the impact of this dependence, this indication should be taken into account when selecting the measurement location and, if possible, avoid measuring at places with local unevenness of the wheel surface (although of course this is not always possible).

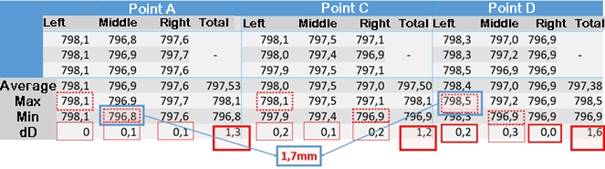
Fig. 2. Summary of the results of measurements with an AA diameter gauge

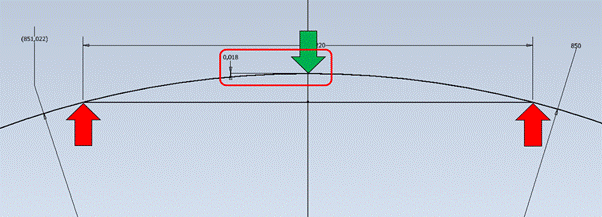
Fig. 3. Parametric model of the three-point diameter measuring system
(the distance of supports was intentionally changed)

Based on this model, wheel defects of different depths were intentionally introduced to illustrate the effect of these local defects on the measurement result of the wheel rolling diameter D.

The selected measuring device was also used to measure the wheel diameter in 23 places every 15.70. This measurement was aimed at determining the wheel ovality. The results obtained are shown in Fig. 5. Despite the relatively high repeatability of measurements at individual points, a significant difference was obtained between the maximum and minimum measured diameter D. In places where extreme values were obtained, the measurement was repeated three times and very good repeatability was obtained. The maximum difference in wheel diameters D measured at 23 points on the circumference is dD₂₃=2.25 mm.

Such a significant difference in diameters may indicate ovality of the wheel or inaccuracy of the applied measurement method (Fig. 4). The obtained average value of the diameter D is D_śr23=797.47 mm. In the comparison of D_śr23 with the average value obtained using a vernier calliper (VC), i.e. D_VC=769.68 mm, a difference of 0.79 mm is obtained. This measurement also indicates that averaging the results of 23 measurements does not guarantee obtaining correct measurement results that could be compared with the criterion |D-D’|.

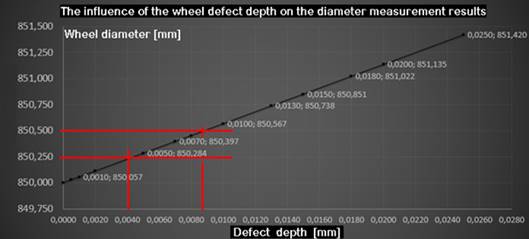
Fig. 4. Graph of changes in the indications of the rolling diameter D resulting from
the local wheel irregularity

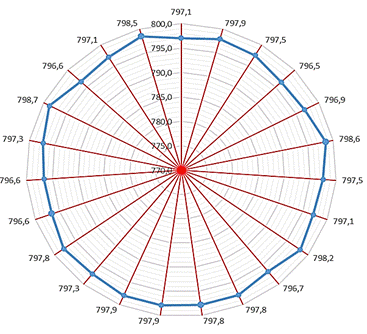
Fig. 5. Visualization of the measurement results of the diameter D [mm] in 23 places on
the circumference of the wheel made with a three-point diameter gauge

In the further part of the work, measurements were performed using other measuring devices, including an optical device. The influence of cleaning the surface before measurement was also verified – Fig. 6. The obtained results indicate that the measurement performed with the optical device (marked in Fig. 6 as CC) before cleaning had a smaller scatter of results, i.e. dD=0.18 mm than after cleaning (shiny surface) dD=0.40 mm. After cleaning, the diameter D_meanCC=796.54 mm was obtained, i.e. 0.56 mm smaller than for the measurement without cleaning. It can therefore be seen that both measurement methods are sensitive to contamination of the measuring surface, however, in the tested case, the CC device overestimated the measurement by 0.56 mm and the result obtained from the three-point diameter gauge marked in Fig. 6 as BB was lower by 0.48 mm in the case of cleaning the wheel surface.

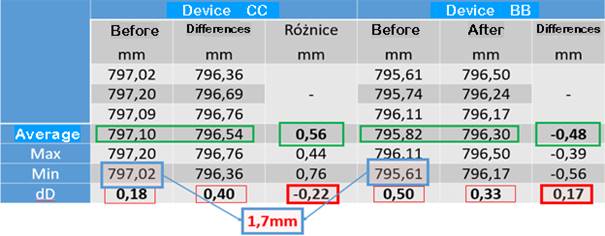
Fig. 6. Summary of measurement results before and after cleaning the surface of the railway wheel

It should be noted that for both the CC and BB devices, the results most similar to the VC vernier calliper are obtained in the case of measurement on a cleaned surface. Taking the average value of D_VCmean=796.68 mm, the difference in relation to the CC measurement on the cleaned surface is d_DVC-CC=0.14 mm and in relation to the BB measurement is
d_DVC-BB=0.38 mm and in relation to the uncleaned surface, respectively
d_DVC-CC=(-0.42) mm and d_DVC-BB=0.86 mm. The test shows that cleaning the measurement site for both the CC and BB devices significantly brings the measurement result closer to the reference value (VC). It is also worth noting that surface contamination in the case of the CC device always overestimated the measurement result and the BB device always underestimated the measurement result in relation to the value obtained after cleaning.

Fig. 7. View of the vernier calliper measurement with measurement bases

To determine the reference value, it was proposed to measure using specially designed measurement bases and a vernier calliper (VC) with a measuring range of 1000 mm and an accuracy of ±0.02 mm – Fig. 7.

6. CONCLUSIONS AND DIRECTIONS FOR FURTHER WORK

Based on the conducted research, it was found that:

• there is an urgent need to standardize the requirements for the maintenance criteria for wheel set geometry, in particular in the |D-D’| and |Dmax-Dmin| criteria, and the need to standardize maintenance procedures throughout the European Union along the lines of the introduced TSIs (to increase safety and reduce maintenance costs);

• the tested methods and measuring instruments marked AA, BB, CC, EE showed significant differences in the rolling diameter D. The rolling diameter values obtained ranged from 796.17 mm to 798.50 mm, which gives a difference of 2.33 mm (on one and the same wheel);

• even minimal differences in the measurement performance compared to the measuring instrument manufacturer's recommendations resulted in several times greater differences in the measurement results at a single point (temperature, accuracy of application to bases, calibration, surface cleaning);

• such significant differences in results using different measurement methods exclude the simultaneous use of different measuring instruments for the purpose of determining
|D-D’| for the vehicle;

• in all categories, the best parameters were shown by the vernier calliper, for which the average dispersion at one point was 0.03 mm (14 times smaller compared to CC (0.43 mm) and 4 times smaller compared to AA (0.13 mm));

• an obvious disadvantage of the method using a vernier calliper and measuring bases is the possibility of measuring on a dismantled wheel set;

• in the example implemented, no clear advantage of any measuring device was indicated (except for the vernier calliper);

• significant differences in the diameter were obtained depending on whether the surface was measured in an operational state or cleaned, i.e. on average by -0.56 mm ("the diameter decreased" after cleaning) for the optical device and by 0.48 mm ("the diameter increased" after cleaning) for the internal diameter gauge.

Based on the measurements performed, it can be stated that despite the considerable technical advancement of measuring instruments, the measurement methods used so far without removing the wheel sets from the vehicle are burdened with measurement uncertainty, which is significant in relation to the maintenance criterion |D-D’| < 1 mm. It is advisable to support the measurements performed with another method with higher measurement accuracy, which in the case of obtaining the limit value will allow for unambiguous verification of the difference in the diameter of the wheels in the railway wheel set. It is obvious that the measured parameter is of great importance for the safety of the railway system, as well as a significant impact on operating costs, therefore increasing the accuracy and repeatability of the measurement is particularly justified in this case.

References

1. Announcement of the Minister of Infrastructure and Construction of 27 January 2016 on the announcement of the uniform text of the regulation of the Minister of Infrastructure on the general technical conditions for the operation of railway vehicles. Dz.U. 2016 poz. 226 (replacing Dz.U. 2005 nr 212 poz. 1771). [In Polish: Obwieszczenie Ministra Infrastruktury i Budownictwa z dnia 27 stycznia 2016 r. w sprawie ogłoszenia jednolitego tekstu rozporządzenia Ministra Infrastruktury w sprawie ogólnych warunków technicznych eksploatacji pojazdów kolejowych].

2. Commission regulation (EU) No 1302/2014 of 18 November 2014 concerning a technical specification for interoperability relating to the ‘rolling stock - locomotives and passenger rolling stock’ subsystem of the rail system in the European Union. Official Journal of the European Union, 2024. TSI Loc&Pas.

3. EN 14363+A2:2023-01 Railway applications – Model tests and simulations of the dynamic properties of rail vehicles before being put into service – Running behaviour tests and stationary tests.

4. EN 13979-1:2020-12 Railway applications – Wheelsets and bogies – Monoblock wheels – Technical approval procedure – Part 1: Forged and rolled wheels.

5. EN 13260:2021-02 Railway applications – Wheelsets and bogies – Wheelsets – Product requirements.

6. EN 15313:2016-05E Railways – Performance requirements for wheel set maintenance – Maintenance of wheel sets of vehicles in service and out of service.

7. EN 13715:2020-12 Railway applications – Wheelsets and bogies – Wheels – Tread profile.

8. PN-92/K-91056 Railway rolling stock – External outline of rims and wheel rims of rimless wheel sets.

9. EN 15302:2022-03 Railways – Parameters of wheel-rail contact geometry – Definitions and evaluation methods.

10. EN 14363+A2:2023-01 Railway applications – Model tests and simulations of the dynamic properties of rail vehicles before being put into service – Running behaviour tests and stationary tests.

11. EN 17095:2019-05 Railway applications – Rolling stock maintenance – Maintenance records.

12. PN-K-91045:2002 Railway rolling stock – Wheel sets – Requirements and test methods.

13. Instructions for measuring and technical evaluation of traction vehicle wheel sets.
Bt-11. PKP Intercity, 2010.

14. Młynarski, S., R. Pilch, M. Smolnik, J. Szybka, G. Wiązania. 2019. “A simulation model for regenerated objects with multiparameter evaluation of technical condition reliability estimation”. Journal of KONBiN 49(2). DOI: 10.2478/jok-2019-0023.

Received 29.09.2024; accepted in revised form 10.11.2024

Scientific Journal of Silesian University of Technology. Series Transport is licensed under a Creative Commons Attribution 4.0 International License

---

[1] Faculty of Transport and Aviation Engineering, The Silesian University of Technology, Krasinskiego 8 Street, 40-019 Katowice, Poland. Email: adam.manka@polsl.pl. ORCID: https://orcid.org/0000-0002-0003-929X