Article citation information:
Kaššay, P., Urbanský, M., Grega, R., Krajňák, J., Kačír, M., Žuľová, L., Kuľka, J. Functional prototype of pneumatic flexible shaft coupling with mechanical constant twist angle regulator. Scientific Journal of Silesian University of Technology. Series Transport. 2024, 125, 115-122. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2024.125.8.
Peter KAŠŠAY[1],
Matej URBANSKÝ[2],
Robert GREGA[3],
Jozef KRAJŇÁK[4],
Matúš KAČÍR[5],
Lucia ŽUĽOVÁ[6],
Jozef KUĽKA[7]
FUNCTIONAL
PROTOTYPE OF PNEUMATIC FLEXIBLE SHAFT COUPLING WITH MECHANICAL CONSTANT TWIST
ANGLE REGULATOR
Summary. Pneumatic couplings
with constant twist angle control are suitable for tuning mechanical systems
where the load torque is proportional to the square of shaft speed. This is
typical mostly for drives of ships used in water transportation. In given
conditions, the coupling maintains the ratio of natural torsional frequency to
rotational speed of the mechanical system at a constant value. With proper
setting of constant twist angle, resonance with harmonic excitation components
in a specific range of operating speed can be avoided. The goal of this
article is to present a design of a newly built prototype of coupling with
mechanical constant twist angle regulator. During further research, it is
planned to be tested in laboratory conditions.
Keywords: pneumatic shaft coupling, constant twist angle
control, mechanical regulator, pneumatic spring, variable stiffness, fan
characteristics, semi-active vibroisolation
1. INTRODUCTION
Pneumatic shaft couplings, as elements of
transport machine drives, are a relatively new devices suitable for providing
semi-active torsional vibration control. The torsional stiffness of these
couplings can be changed during operation by adjusting the air pressure in
their pneumatic elements. Pneumatic elements have been commonly used for tuning
rectilinear vibration for a long time [10]. In the area of torsional
vibration, several tuning methods have been elaborated for utilization of
pneumatic shaft couplings [4]. One of them, the constant twist angle control
method, or sometimes called also as autoregulation, is designed especially for
mechanical systems where the load torque is proportional to the square of shaft
rotational speed, which we can encounter in marine and fan drives. With proper
setting of constant twist angle, resonance with harmonic excitation components
in specific range of operating speed can be avoided [4]. As this article
focuses on description of coupling prototype design we will not go into details
any further, an interested reader can find detailed description of constant
twist angle control in works [4, 5, 8, 9]. A common solution to problems
associated with torsional oscillation is a selection of proper torsional
flexible coupling. A coupling with suitable torsional stiffness ensures that
the natural torsional frequency of the mechanical system is far enough away
from the excitation frequency of any load torque harmonic component. But as
marine drives are working usually in a wide range of operating speeds, avoiding
resonance in full range of operating speed can be problematic [3, 11, 13]. One solution is to use highly
flexible couplings with low torsional stiffness, ensuring that the natural
frequency is always lower than the excitation frequencies; thus, the system is
running in supercritical area [4]. Another solution is to use flexible
couplings with non-linear progressive load characteristics, where the torsional
stiffness is dependent on load torque. Proper non-linear load characteristics
can provide avoidance of resonance in a wide range of speed [3, 4]. On the
contrary, improper non-linear load characteristic causes that system remains in
resonance area in wider range of operating speed [11]. Another problem with classic
flexible couplings using rubber flexible elements is that their torsional
stiffness depends on temperature, loading frequency, number of completed work
cycles and age of rubber [7]. So then during operation the
mechanical system can be out of tune. Because of that, some authors recommend
to use high safety factors for such flexible shaft couplings [3]. Pneumatic
flexible shaft coupling’s properties are much less sensitive to such influences
[4]. We also want to mention that there are flexible couplings with adjustable
stiffness based on other than pneumatic principles too [6, 12].
The main goal of this article is to present a
prototype of pneumatic flexible shaft coupling with mechanical constant twist
angle regulator produced for the purpose of subsequent laboratory testing.
2. DESCRIPTION OF PNEUMATIC COUPLING
PROTOTYPE
The presented coupling was designed
with focus to make a system with as simple as possible with a fully mechanical
constant twist angle regulator without any electronic components. We also
wanted to use, if possible, only standard pneumatic elements available on the market.
In one of previously published works [5] the
authors presented an electronic constant twist angle control system.
In Fig. 1 the main view and in Fig.
2 the partial side view of coupling are shown.
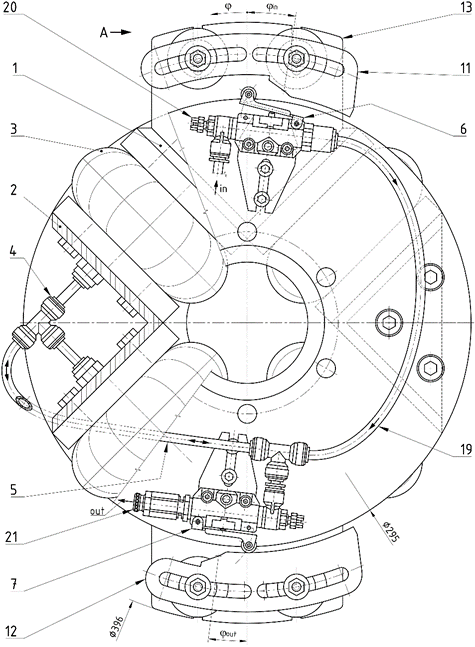
Fig. 1. Pneumatic flexible shaft coupling with mechanical constant twist
angle regulator
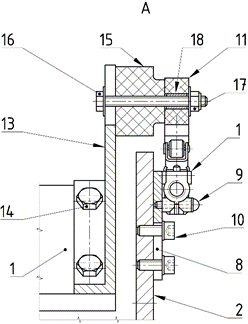
Fig. 2. Pneumatic flexible shaft coupling with
mechanical constant twist angle regulator, detail of cam and roller valve
connection
At first, we will describe only the
mechanical composition of coupling the assembly and the function of the
regulator will be described afterwards.
The coupling consists of a driving
body which main part is a driving disc (1)
and a driven body which main part is a driven disc (2), the driving and driven bodies are connected with pneumatic
springs (3) ensuring the possibility
to accommodate radial, angular and axial misalignments of connected shafts and,
last but not least, flexible torque transmission. The internal volumes of the
springs are interconnected via pneumatic tubes and fittings. The filling and
discharge of compressed air into the coupling’s compression space are realized
with Push-In T/connector (4) and a
pneumatic tube (5). In figure (Fig.
1), the direction of air flow in the pneumatic tubes is shown by arrows. The
filling and discharging of compressed air into the coupling are controlled by a
system of roller lever valves mounted on the driven disc and cams located on
the driving disc.
The inlet roller valve (6) and outlet roller valve (7) are the part of the driven body.
They are located on holding plates (8) attached
to driven disc (2). The roller valves
are fixed to the holding plates with screws (9).
The holding plates themselves are attached to the driven body through straight
slots with screws (10), this ensures
the possibility to adjust their radial position to the coupling’s axis.
The inlet cam (11) and outlet cam (12),
controlling the respective inlet and outlet roller valves, are part of the
driving body. For manufacturing the cams, the 3D printing method has been used
which is a very modern approach in the field of rapid prototyping [1, 3]. The cams are mounted on plates
(13) attached to the driving disc
with screws (14). The proper axial
position of the cams is ensured by spacer rings (15).
The connection of the cams to the
plates is realized with bolts (16),
nuts (17), the previously mentioned
spacer rings and cylindrical cases (18).
The radial position of the cams, similarly to the roller valves, can be
properly adjusted as the bolts are located in straight slots of plates. The
tangential position of the cams, is adjustable too, as they are mounted through
circular arc slots. The tangential position of the cams determines the values
of inlet angle jin and
outlet angle jout
when the corresponding valves are just opened (or closed).
The compressed air is fed into the
coupling trough inlet (in Fig. 1 marked with an arrow labeled as in). The inlet and outlet valve are
connected with a pneumatic tube (19).
Both the inlet and outlet valve have an adjustable throttle valve (20) on the input that we can adjust the
airflow rate if needed. The discharge of compressed air from the coupling is solved
with an adjustable safety valve (21),
so the operating pressure cannot drop under the selected minimum value.
The pneumatic coupling, as shown in
Fig. 1, is in a neutral position at zero twist angle. For the presented
prototype design, we consider only one direction of rotation. The direction of
twisting of the driving disc (cams) to driven discs (roller valves) is marked
with arrow labelled as j. By disassembling the cams and
flipping them around, the opposite direction of twisting can be obtained.
A photo of a manufactured coupling
prototype is shown in Fig. 3.

Fig.
3. Photo of a manufactured pneumatic coupling prototype
The ideal function of coupling when
loaded with slowly increasing torque T from
zero to maximum and then decreasing it back to zero can be described according
to illustrative figure Fig. 4.a). This cycle is shown with a wide continuous
line. In neutral position at zero twist angle j = 0, when the coupling is unloaded,
the outlet roller valve is opened as the outlet roller valve is activated with
outlet cam and the inlet valve is closed (see Fig. 1 too). The compressed air
in the coupling can flow out until it reaches the minimum value pmin set by the safety valve.
After we start increasing the load torque, the twist angle starts to increase.
Now the coupling works on the load characteristics corresponding to minimum
pressure pmin. Load
characteristics at different pressures (pmin
< p1 … < p3 < pmax) are shown in Fig. 4.a). The pressure in coupling
remains on minimum value until the twist angle reaches the outlet angle jout, then the outlet valve is closed.
Now both valves are closed, and no air flows into or out the coupling. After
reaching the inlet angle jin,
the inlet roller valve starts releasing compressed air from the inlet tube to
the coupling and tries to hold the twist angle on this value (jin) until the load torque reaches the value
corresponding to maximum pressure pmax.
From this point, the load characteristics of coupling are corresponding to load
characteristics at maximum pressure. When decreasing the load torque, at first,
the coupling works at maximum pressure. Then, after reaching the inlet angle,
both valves are closed until we reach the outlet angle. Now the control
mechanism tries to maintain the twist angle at this value (jout) until we reach the minimum
pressure, and after this, the coupling works at minimum pressure. The inlet
angle and outlet angle can be independently set to desired values by changing
the tangential positions of the respective cam. If, in the described process,
we insert an in-between cycle (illustrated with semi-bold dashed lines) when
increasing the torque at inlet angle we reach pressure p3 so that now we slowly decrease the torque, the
pressure remains on value p3
until we reach the outlet angle the control system opens the outlet valve and
tries to maintain this deflection. Let say, now we decrease the torque until
pressure p1 is reached,
and again we start slowly increase the torque. Between the inlet and outlet
angle when both valves are closed, the coupling works at characteristics with
pressure p1. We can say
that the range between the inlet and outlet angles is the deadband of the
regulator, where the valves remain closed and the coupling works at constant
pressure.
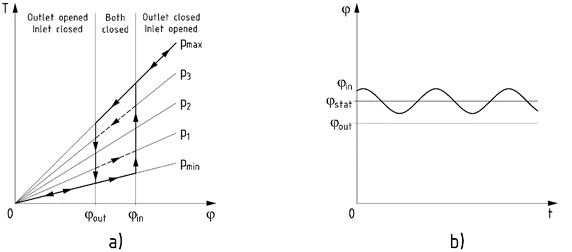
Fig. 4. Illustration of the
mechanical constant twist angle control system working principle
a) under static loading, b) under dynamic loading in steady state
The working principle of the
coupling loaded with periodical load torque (consisting of static and dynamic
component) is shown in Fig. 4.b). The graph in Fig. 4.b) shows a periodical
course of twist angle j in time t. The control mechanism adjusted the pressure so that after
reaching a steady-state condition, the static twist angle jstat corresponding to the static load
torque lies between the inlet and outlet angles. Properly set inlet angle jin and outlet angle jout must allow the coupling to
oscillate within the deadband of the regulator without activating the valves.
After changing the operating speed (static torque), the regulator automatically
adjusts the twist angle back inside the deadband.
3. CONCLUSIONS
The
greatest advantage of the presented coupling is that the fully mechanical
regulator has a very simple design using only standard pneumatic components.
Also, no electrical supply or expensive electronic control is needed. That is
why we think that the presented coupling will be a useful contribution in the field of
drives used in water transport.
From the presented
information, we can also deduce some possible issues or let us say interesting
ideas for future research:
·
At first, the desired constant (static) twist angle
cannot be set directly as with an electronic control system [5]. We only select the deadband in which the static twist angle should lie.
This should be quite narrow, to have as small as possible difference of static
twist angle from ideal value. But it cannot be too narrow because the twist
angle time course in a steady state must fit into the deadband. Therefore,
these angles must be properly determined to ensure proper function in the full
operation speed range. In the future, a more sophisticated mechanical regulator
capable of working with the mean value of twist angle could be developed.
·
Another possible issue is that between the neutral
position and the outlet angle, the coupling works at minimum pressure. This can
be resolved by using more complicated cams or adjustable cam systems which
provide preliminary inflation of the coupling at a specific angle smaller than
the outlet angle.
In the follow-up research, the
authors plan to test the coupling under static and dynamic loading to compare
assumptions presented here with the actual measured results and subsequently
develop a method for the reliable determination of the inlet and outlet angle
based both on preliminary torsional analysis and experiments.
Acknowledgments
This paper was written within the framework of
the following grant projects:
·
KEGA 037TUKE-4/2024: Creation of
interactive tool for increasing of students’ skills and competences in teaching
of study subjects relating to elaboration of drawing documentation,
·
KEGA 044TUKE-4/2024: Application of
virtual and augmented reality into education in order to innovate mechanical
engineering study programs.
References
1.
Fabian Michal, Róbert Huňady, František
Kupec. 2023. „Reverse
Engineering and Rapid Prototyping in the Process of Developing Prototypes of
Automotive Parts”. Manufacturing
Technology 22(6): 669-678. DOI: 10.21062/mft.2022.084.
2.
Fabian Michal, František Kupec. 2021. „Use of 3D Parametric Models in the
Automotive Component Design Process”. Advances
in Science and Technology Research Journal 15(1): 255-264. DOI:
10.12913/22998624/132589.
3.
Feese Troy. 2017. „Coupling Failures in VFD Motor Fan Systems
Due To Torsional Vibration”. In: Torsional Vibration Symposium: 1-15. The
Vibration Association, Hallwang, Austria. 17-19 May 2017, Salzburg, Austria.
5.
Homišin Jaroslav, Peter Kaššay, Matej
Urbanský, Michal Puškár, Robert Grega, Jozef Krajňák.
2020. „Electronic Constant Twist Angle Control System Suitable for Torsional
Vibration Tuning of Propulsion Systems”. Journal of Marine Science and Engineering 8(9):
721. DOI: 10.3390/jmse8090721.
6.
Kinnunen Kalle, Sampo
Laine, Tuomas Tiainen, Raine Viitala. 2022.
„Method for Adjusting Torsional Natural Frequencies of Powertrains with Novel
Coupling Design”. Machines 10(3):
162. DOI: 10.3390/machines10030162.
7.
Opasiak, Tadeusz, Jerzy Margielewicz, Damian Gąska,
Tomasz Haniszewski. 2022.
„Influence of Changes in the Working Temperature of Flexible Couplings on Their
Stiffness Characteristics”. Transport
Problems 17(4): 177-86. DOI: 10.20858/tp.2022.17.4.15.
11. Wachel
J.C. (Buddy), Fred R. Szenasi. 1993. „Analysis of Torsional Vibrations in
Rotating Machinery”. In: Proceedings of
the Twenty-Second Turbomachinery Symposium: 127-151. Texas A&M
University. Turbomachinery Laboratories, College Station, Texas, USA. 1993. DOI: 10.21423/R1K95J.
12. Wieczorek Andrzej Norbert, Łukasz Konieczny, Grzegorz Wojnar, Rafał Wyroba,
Krzysztof Filipowicz, Mariusz Kuczaj. 2024.
„Reduction of Dynamic Loads in the Drive System of Mining Scraper Conveyors
through the Use of an Innovative Highly Flexible Metal Coupling”. Eksploatacja i Niezawodnosc – Maintenance
and Reliability 26(2): 181171. DOI: 10.17531/ein/181171.
Received 29.07.2024; accepted in revised form 05.10.2024
![]()
Scientific
Journal of Silesian University of Technology. Series Transport is licensed
under a Creative Commons Attribution 4.0 International License