Article citation information:
Grzybowski, M., Młyńczak, J., Sokołowska, L., Matowicki, M. Software requirements elaboration with decision tables. Scientific Journal of Silesian University of Technology. Series Transport. 2024, 125, 89-99. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2024.125.6.
Michał
GRZYBOWSKI[1], Jakub MŁYŃCZAK[2], Lucyna SOKOŁOWSKA[3], Michał MATOWICKI[4]
SOFTWARE
REQUIREMENTS ELABORATION WITH
DECISION TABLES
Summary. The paper describes
decision table notation as a requirements definition technique. Modern critical
systems, e.g., railway signaling systems, are implemented with electronic
technologies. The use of computers in these systems has greatly expanded their
functionality. Increase in functionality unfortunately leads to increase in
complexity, which forces the designer to follow a more rigorous development
process. The paper discusses the subject of describing expected software
behavior, i.e., software requirements specification. It presents desired
requirements features and describes how these features can be obtained by use
of decision tables. The paper also discusses decision table transformations,
which can reduce the effort to establish decision tables and facilitate their
analysis. The authors’ experiments support the use of decision tables as a mean
to increase requirements quality by providing tools for automatic decision
table processing.
Keywords: decision tables, software engineering,
semi-formal methods
1. INTRODUCTION
Modern safety critical systems, such as railway
signaling systems, are implemented with computer technology. Use of computers
allows for greater functionality. Unfortunately, greater functionality is
occupied with greater complexity, which forces the designer to follow a more
rigorous development process in order to achieve target software reliability.
More systematic development process in safety critical systems often follow
recommendations of IEC 61508 standard or similar, domain-specific ISO 26262, DO-178C
or EN 50716 [1]. These standards point out the requirements setting phase as
one of the initial development steps. In authors’ opinion this phase is
critical for development because defects introduced in this phase can be
potentially carried through the rest of the development process and remain
uncovered until overall requirement testing or even validation.
Requirements in essence describe expected
properties of developed software. The properties may be of various natures, but
the most basic part is the functional requirements, which describe how software
shall behave – what it shall do, how it shall react to external stimuli. This
underlines the importance of requirements in the entire development process.
Software development is always aimed at obtaining software, which implements
certain behaviors. If the behavior description is too terse or vague, then the
end result may not satisfy user expectations, even if the rest of the process
is executed flawlessly.
Requirements management is a mature software
engineering discipline documented in literature, for example in [7]. Works
concerned with requirements management discuss properties of requirements
themselves. There are many such qualities, but the most basic are:
· Completeness
– requirements need to be complete, i.e., describe all expected properties of
the software.
· Correctness
– requirements need to describe features as they should be implemented. In
particular, requirements should not be contradictory.
· Realizability
– requirements need to be possible to implement. Singular requirements are
rarely not realizable, but a set of requirements possibly can be not
realizable, for example if the requirements are contradictory.
· Unequivocalness
– requirements need to be interpretable only in one way; otherwise, there is a
risk of introducing defect due to requirement misinterpretation.
· Verifiability
– requirements need to be specified in a way, which allows for deciding whether
a particular program implements the requirement or not.
· Traceability
– in most safety-critical software development processes, it is recommended to
demonstrate how requirements have been implemented and how they have been
verified to be implemented correctly. In order to achieve this, requirements
need to be specified in a way which allows tracing them to artifacts which
implement them or support verification of correct implementation.
Requirements quality can be improved by making
them more structured. One notation designed for such use is notation of
decision tables ([3, 4]).
This paper discusses use of decision tables for
requirements specification and decision tables transformations, which
facilitate their design and analysis. In particular, the paper discusses
possible decision table interpretations and transformation between equivalent
decision tables written for different interpretations. Prior research discussed
properties of decision tables and methods for automatic derivation of computer
programs from decision tables ([6]). This work recognizes that decision tables
can be interesting objects in their own right and that there are useful
algorithms, which transform decision tables into other decision tables.
2. METHODS
2.1. Decision tables
The decision table is an easy-to-use
notation for describing rule systems ([2]). The notation is not standardized,
it should be rather treated as a notation family. Notations in this family have
certain common features:
1. They are described in tabular form,
2. They describe rules of
decision-making based on given criteria,
3. For brevity, they allow specifying
that a particular criterion is not considered in a particular rule.
An example decision table is
presented in Tab. 1.
Tab.
1
Decision
table structure (source: original work)
|
Criterion 1 |
Criterion 2 |
Criterion 3 |
Decision 1 |
Decision 2 |
|
Value11 |
Value12 |
Value13 |
Decision11 |
Decision12 |
|
Value21 |
* |
* |
Decision21 |
Decision22 |
|
* |
* |
Value33 |
Decision31 |
Decision32 |
The
rest of the paper will discuss decision tables in the form given in Tab. 1:
1. The table
consists of two parts – a criterial part (rule premises) and a decisional part
(decision made based on rule premises); decision table parts are separated by
double line.
2. Criteria
and decisions are specified as columns (in the decision table in Table 1, there
are three criteria and two decision components).
3. Rules are
written in the table rows; each row specifies rule criteria and decision.
4. The symbol
‘*’ may be used instead of a criterion, denoting that criterion does not affect
the decision in the considered rule.
Decision table shall be interpreted
as follows (interpretation I): table associates criterial vectors (values of
criterial columns) with decision vectors (values of decision columns).
Criterial vector is associated with decision vector of the rule, which
criterial columns match corresponding elements of criterial vector or which
contain symbol ‘*’.
It should be noted, that in this
interpretation a single criteria vector can be associated with 0, 1 or more
decisions by the decision table. In practical applications one can also find
another interpretation (interpretation II), in which the criteria vector is
associated with the decision vector specified by the first rule (from the top)
of the decision table, which satisfies the condition above. In such
interpretation, criteria vector can be associated only with 0 or 1 decision
vectors, which reduces the effort to design an unequivocal decision table.
According to the above description, the decision table in Table 1 associates criteria vector (Value11, Value12, Value13) to decision vector (Decision11, Decision12). Vector (Value21, arbitrary value, Value23) is associated with:
·
Decision vectors (Decision21,
Decision22) and (Decision31, Decision32) in
interpretation I,
·
Decision vector (Decision21,
Decision22) in interpretation II.
It should be noted that the
literature discusses decision table interpretation in greater detail, for
example in [5]. In the authors’ opinion, interpretation rules given in [5] are
needlessly complex. The Interpretation rules presented in this section are
clearer and yet precise enough to allow for automated decision table
manipulation.
Decision table can be analyzed
depending on multiple criteria. A decision table is complete, if it associates
every possible criteria vector to some decision vector, i.e., it specifies a
decision for each criteria combination. This definition agrees with intuition –
decision table is complete if it allows one to decide in any possible situation
(for each criteria combination).
A decision table is consistent, if
it associates every possible criteria vector with at most one decision vector.
Intuitively, if a consistent decision table determines a decision, then it only
determines a single decision for a particular situation. An inconsistent
decision table associates at least one criteria vector with two contradictory
decision vectors.
2.2. Decision table examples
A decision table allows for the
description of various decision-making processes. This paragraph presents an
example of a decision table application for the specification of business rules
and for the specification of finite automata.
Consider an application to business
rules specification. Some Polish cities run programs aimed at increasing
interest in public sport facilities. The city council of City A agreed to
reduced ticket prices for public recreation facilities according to following
rules:
1. For A
residents, ticket prices are reduced by 50%,
2. For large
family card holder, ticket prices are reduced by 30%,
3. For
pensioners, ticker prices are reduced by 50%,
4. Ticket
price reductions for A residents and pensioners are independent,
5. Ticket
price reductions for A residents and large family card holders are independent,
6. Ticket
price reductions do not compound except above situations.
The above rules are specified as a
decision table in Tab. 2. It should be pointed out that the above description
contains imprecise statements (e.g., “reductions are independent”, “reductions
don’t compound”). Specification of business rules in the form of decision table
facilitates their understanding.
Tab.
2
Example decision
table – ticket price reductions (source: original work)
|
A resident |
Large family card holder |
Pensioner |
Ticket price reduction |
|
Yes |
No |
No |
50% |
|
No |
Yes |
No |
30% |
|
No |
No |
Yes |
50% |
|
Yes |
No |
Yes |
75% |
|
Yes |
Yes |
No |
65% |
|
No |
No |
No |
0% |
|
Yes |
Yes |
Yes |
75% |
|
No |
Yes |
Yes |
50% |
The decision table in Tab. 2
contains 8 rows – it explicitly associates each criteria vector with a
decision. Based on a simple analysis, the decision table can be reduced to the
form given in Tab. 3.
Tab.
3
Example
decision table – ticket price reductions
(after simplification, source: original work)
|
A resident |
Large family card holder |
Pensioner |
Ticket price reduction |
|
Yes |
No |
No |
50% |
|
No |
Yes |
No |
30% |
|
No |
* |
Yes |
50% |
|
Yes |
* |
Yes |
75% |
|
Yes |
Yes |
No |
65% |
|
No |
No |
No |
0% |
A second example presents the application of decision tables to the description of a stateful system. This example considers signaling at a pedestrian crossing, i.e., system controlling the road signal (RD) and pedestrian signal (PD) at the pedestrian crossing. The system behavior can be summarized as follows:
1. In the
basic state, RD displays a green light, and PD displays a red light.
2. Signal
lights changes are initiated by pressing a pushbutton.
3. In order
to assure traffic flow, the pushbutton press is memorized, but it does not
cause an immediate signal light change for certain time after signal change on
RD to a green light.
4. As a
result of the pushbutton press, RD and PD light change sequence is initiated:
a. Yellow
light on RD and red on PD
b. Red light
on RD and green on PD
c. Red light
on RD and flashing green on PD,
d. Red light
and yellow light on RD and red on PD,
e. Green
light on RD and red on PD (basic state).
The behavior of such a system is
often described using finite automata, in this case with the R (cycle request)
automaton and the S (signaling sequence) automaton, presented in Fig. 1 and
Fig. 2.
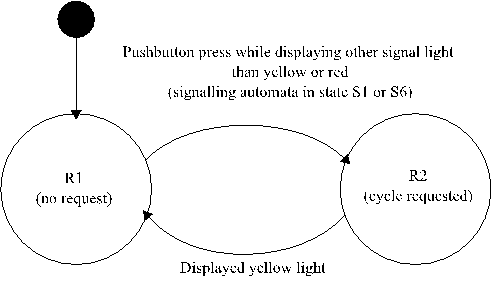
Fig. 1. R (Cycle request) automaton
(source: original work)
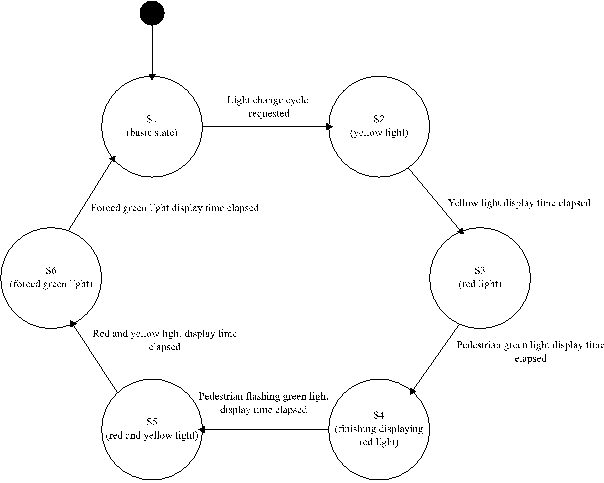
Fig. 2. S (Signaling sequence)
automaton (source: original work)
System behavior can be described
with he decision tables provided in Tab. 4 and Tab. 5.
Tab.
4
Example decision table –
R automaton (source: original work)
|
R automaton state |
S automaton state |
Pressed pushbutton |
New R automaton state |
|
R1 |
S1 |
Yes |
R2 |
|
R1 |
S6 |
Yes |
R2 |
|
R1 |
* |
* |
R1 |
|
R2 |
S2 |
* |
R1 |
|
R2 |
* |
* |
R2 |
Tab.
5
Example decision table –
S automaton (source: original work)
|
S automaton state |
R automaton state |
Current light display
time elapsed |
New S automaton state |
Start counting light
display time |
RD signal light |
PD signal light |
|
S1 |
R2 |
* |
S2 |
Yes |
Yellow |
Red |
|
S1 |
* |
* |
S1 |
No |
Green |
Red |
|
S2 |
* |
Yes |
S3 |
Yes |
Red |
Green |
|
S2 |
* |
No |
S2 |
No |
Yellow |
Red |
|
S3 |
* |
Yes |
S4 |
Yes |
Red |
Flashing green |
|
S3 |
* |
No |
S3 |
No |
Red |
Green |
|
S4 |
* |
Yes |
S5 |
Yes |
Red and yellow |
Red |
|
S4 |
* |
No |
S4 |
No |
Red |
Flashing green |
|
S5 |
* |
Yes |
S6 |
Yes |
Green |
Red |
|
S5 |
* |
No |
S5 |
No |
Red and yellow |
Red |
|
S6 |
* |
Yes |
S1 |
No |
Green |
Red |
|
S6 |
* |
No |
S6 |
No |
Green |
Red |
Decision tables have certain advantages for
describing finite automata:
1. They
describe state change criteria unequivocally, reducing the risk of
misinterpretation. There can be situations in which an automaton may perform
one of many possible state transitions. A graphical automaton model may not be
precise enough to indicate which transition shall be performed in such a case.
2. They are
traceable – while a figure is useful to provide an overview of expected
behavior, it usually does not allow for systematic enumeration of transitions.
In decision tables notation this is trivial, for example, by enumerating
decision table rows.
3. They allow
for the clear presentation of additional information (for example, the lights displayed by RD and PD signals in the
case of the S automaton description).
2.3. Decision table processing
The syntax and semantics of decision
tables are precise enough to allow the construction of algorithms for their
analysis and transformation. This section presents a description of selected
algorithms.
2.3.1. Decision table processing
Decision tables used for
requirements specification need to be complete and consistent (if interpretation
I is used). Analysis of these properties can be carried out automatically by an
algorithm.
Decision table completeness can be
analyzed as follows:
1. Generate
all possible criteria vectors,
2. Check, if
the decision table associates each criteria vector with at least one decision.
3. If there
is at least one criteria vector not associated with any decision by the
decision table, then the decision table is not complete.
Decision table consistency can be
analyzed as follows:
1. For each
decision table rule A:
a. Consider
each decision table rule B following rule A:
i.
Select criterial column,
ii.
Check if either both rules have the same
value in the selected criteria column or one is ‘*’. If yes, then go to step
iii, otherwise select the next rule (B),
iii.
If not all criteria columns have been
checked, then select next criteria column and go to step ii,
iv.
Check, if decision vectors of A and B
rules are equal – if not, then the decision table is not consistent (rules A
and B can be applied to one criteria column and have contradictory decisions) –
end of algorithm,
2. If all
decision table rules A have been considered and no inconsistency has been
detected, then the decision table is consistent.
Using the above algorithms, it can
be checked, that S and R automaton decision tables presented in section 2.2 are
complete, but are not consistent (in interpretation I):
·
In case of R automaton decision table,
contradictory are rules in the first and third row – they associate criteria
vector (R1, S1, Yes) with decisions R2 and R1,
·
In case of S automaton decision table,
contradictory rules are in the first and second row – they associate criteria
vector (S1, R2, No) with decisions (S2, Yes, Yellow, Red) and (S1, No, Green,
Red).
2.3.2. Decision table expansion
This section presents the first transformation defined by the authors. It is the most basic transformation, which intuitively generates an equivalent decision table (i.e., associating criteria vectors with the same decisions), that explicitly associates each criteria vector with its corresponding decision vector. Decision table expansion proceeds as follows:
1. Start with
an empty rule list,
2. For each
possible criteria vector:
a. Check if
the considered decision table associates the criteria vector with any decision.
If no, consider the next criteria vector,
b. Add a rule
associating the considered criteria vector with the corresponding decision
vector to the rule list,
3. Construct
a decision table containing all rules from the rule list.
The algorithm is very simple, but
the created decision tables have certain useful features – the resulting
decision tables do not contain symbol ‘*’ and are always consistent. This makes
them useful for further processing. Algorithms processing them do not need to
consider the order of rules in the decision table.
2.3.3. Redundant rule elimination
This section presents the second
transformation defined by the authors. Decision tables obtained from decision
table expansion can be useful for further software processing, but they may be
too large for manual use. As can be easily seen, if a decision table has n
criteria columns and ith column can have Mi values,
then the number of rules R is:
![]() (1)
(1)
To facilitate decision table handling, it is useful to reduce the number of decision table rules without changing their meaning, which can be done by recreating the ‘*’ symbol in decision table rules in a controlled fashion. The algorithm is as follows:
1.
Select the first decision table rule.
2.
Select the first criteria column.
3.
Generate a temporary criteria pattern,
which consists of the considered rule criteria part with the selected criteria
column value replaced with ‘*’.
4.
Check if each criteria vector matching the
generated temporary criteria pattern is associated with the same decision as
the decision part of the considered rule. If yes, go to step 5, otherwise go to
step 8.
5.
(Check in step 4 successful) Replace the
criteria part of the considered rule with the temporary criteria pattern.
6.
Remove from the decision table any rule
subsumed (criteria part being a specialization of the criteria part of the
considered rule) by the considered rule.
7.
Go to step 1.
8.
(Check in step 4 unsuccessful) If the
selected criteria column is not the last, then select the next and go to step
3.
9.
If the selected rule is not the last, then
select the next rule and go to step 2.
10. End of the
algorithm – the decision table does not contain any redundant rule.
3. RESULTS AND DISCUSSION
As noted in section 2.3.1, decision
table properties can be analyzed automatically. The authors’ designed a
prototype implementation of these algorithms and the decision table
transformations specified in sections 2.3.2 and 2.3.3. The latter algorithms, proposed
by the authors, allow for the automatic generation of decision tables in
interpretation I that are equivalent to the given decision tables designed for
interpretation II. The prototype implementation has been developed in Scheme.
The implementation of all four algorithms requires 272 lines of source code,
which stems from the simplicity of the algorithms. Nevertheless, these
algorithms are useful for designing and analyzing requirements in the form of
decision tables. In authors’ opinion, decision tables together with proposed
algorithms facilitate the elaboration of requirements with the features
mentioned in section 1:
1. Completeness
– the decision table completeness analysis algorithm allows for automatic
checking if decision-making rules specified in the decision table cover all
possible scenarios,
2. Correctness
– the decision table correctness analysis algorithm allows for automatic
checking that input decision table in interpretation I is consistent; the
decision table expansion and redundant rule elimination algorithms allow for
the automatic generation of consistent decision tables in interpretation I
based on input decision tables in interpretation II,
3. Realizability
– decision table semantics assures realizability, which is additionally
facilitated by the presented algorithms for the translation of decision tables
in interpretation II into consistent decision tables in interpretation I,
4. Unequivocalness
– decision table semantics provide precise interpretation rules,
5. Verifiability
– consistent decision tables in interpretation I allow for direct specification
of test cases based on the decision table structure; automatic algorithms for
the translation of decision tables in interpretation II into consistent
decision tables in interpretation I allow for simple test case specification
for decision tables in interpretation II as well,
6. Traceability
– decision tables are evidently traceable,
for example, by tracing individual decision table rows.
4. CONCLUSIONS AND SUMMARY
The paper discusses the use of decision
tables for requirements specification and their advantages. It also points out
the possibility of automatic decision table processing and presents a novel
algorithm for translating decision tables designed for interpretation II into
consistent decision tables in interpretation I. The algorithms proposed by the
authors facilitate requirement design and analysis. The authors have developed
a prototype implementation of these algorithms, which validates the proposed
methods.
In the authors’ opinion, automatic
decision table processing can be further researched to reduce the effort needed
for producing other artifacts in the development process based on decision
tables. The previous section sketched the relationship between decision tables
and test cases, which warrants additional investigation. The authors suspect
that similar methods to those presented should also allow for the use of
decision tables with formal methods, for example, by automatic translation of
decision table rules into logic propositions usable in formal specifications.
References
1.
EN 50716. Railway Applications -
Requirements for software development. Brussels: CENELEC.
2.
Huysmans Johan, Karel Dejaeger, Christophe
Mues, Jan Vanthienen, Bart Baesens. 2011. „An empirical evaluation of the comprehesibility of decision table, tree
and rule based predictive models”. Decision Support Systems 51(1):
131-154. DOI: https://doi.org/10.1016/j.dss.2010.12.003.
3.
Jorgensen Paul C. 2010. Modeling
Software Behavior: A Craftsman’s Approach. Boca Raton: CRC Press. ISBN:
978-1-4200-8076-6.
4.
King Peter J.H. 1967. „Decision
Tables”. The Computer Journal 10(11): 135-142. DOI: https://doi.org/10.1093/comjnl/10.2.135.
5.
King Peter J.H. 1969. „The
interpretation of limited entry decision table format and relationships among
conditions”. The Computer Journal 12(4): 320-326. DOI: https://doi.org/10.1093/comjnl/12.4.320.
6.
Pooch Udo W. 1974. „Translation of Decision Tables”. ACM Computing Surveys 6(2):
125-151. DOI: https://doi.org/10.1145/356628.356630.
7.
Wiegers Karl, Joy Beatty. 2013. Software
Requirements. Redmond: Microsoft Press. ISBN:
978-0-7356-7966-5.
Received 08.06.2024; accepted in revised form 30.08.2024
![]()
Scientific
Journal of Silesian University of Technology. Series Transport is licensed under
a Creative Commons Attribution 4.0 International License