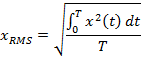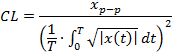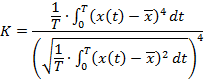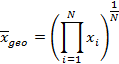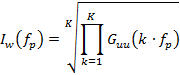Article citation information:
Grega, R., Czech, P. Non-invasive vibroacoustic diagnostics of car internal combustion engines. Scientific Journal of Silesian University of Technology. Series Transport. 2024, 125, 69-87. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2024.125.5.
Robert GREGA[1], Piotr CZECH[2]
NON-INVASIVE
VIBROACOUSTIC DIAGNOSTICS OF CAR INTERNAL COMBUSTION ENGINES
Summary. Over the past ten
years, the number of vehicles on the roads has almost doubled. The consequences
of this state are negative effects, which include an increased number of road
accidents and an increased level of harmful emissions into the atmosphere, along
with other forms of environmental pollution. Road safety level is the sum of
the safety levels of each element of the human-vehicle-environment system. In
order to maintain the appropriate level of road safety, vehicles must be
maintained in proper technical condition, and for this purpose, it is necessary
to detect all types of damage at an early stage. All types of methods that
allow non-invasive diagnosis of the technical condition of vehicles and their
individual components seem to be extremely useful. It is important that they
allow for detecting emerging faults in their early stages of development. Such
tools undoubtedly include methods using vibration and acoustic signals as
carriers of information about technical condition. Their appropriate processing
and use in diagnostic systems that additionally use artificial intelligence
makes it possible to meet the requirements for diagnostic systems. From a
global perspective, this additionally enables the impact on reducing the costs
of civilization development, including social costs. The article presents the
use of various methods of processing vibroacoustic signals and artificial
intelligence tools used to diagnose damage to combustion engines in cars.
Keywords: diagnostics, automotive internal combustion
engines, vibroacoustics, non-invasive diagnostic methods
1. INTRODUCTION
Motor
vehicles powered by internal combustion engines dominate the roads around the
world. Automotive companies, trying to gain new customers, offer them
increasingly perfect, ergonomic, economical, more reliable, more durable, safer
and more ecological products. All these features are important for vehicle
users, but in the social aspect, safety, and ecology are the most important.
Road
safety depends on many factors. These factors can be analyzed as interactions
in the human-vehicle-environment system. The level of road safety is the sum of
the safety levels of each of the elements of this system [1, 2].
The
risk of accidents in road traffic is the possibility of a collision between
vehicles, a vehicle and a human being, or a vehicle and a stationary obstacle.
The calculation shows that in each of these three situations, the vehicle is
the basic element of the accident risk, so the vehicle mainly affects the level
of road traffic safety and, most importantly, human safety [3].
The
required safety standards are different for cars already in use and for new
cars. In the first case, in order to maintain the appropriate level of road
traffic safety, their technical condition is regularly checked at specialized
diagnostic stations. In the second case, a homologation process is
necessary, taking into account a number of regulations.
It
is extremely important to keep motor vehicles in good technical condition. For
this purpose, it is necessary to detect all types of damage early enough so
that the process of removing it can be undertaken in time. Appropriate
diagnostic means should be available both to people diagnosing vehicles at
diagnostic stations and to mechanics working at service establishments.
Equipping them with appropriate tools would improve the efficiency of their
work and, in a broader sense, improve road traffic safety.
As
research carried out in many centers around the world indicates, one of the
possibilities of obtaining information about the technical condition is through
vibroacoustic phenomena. The selection of these phenomena as sources of
information is due to various reasons, including [4, 5]:
-
vibrations
are a reflection of the most important physical processes that determine proper
functioning,
-
vibroacoustic
vibrations, as information carriers, are characterized by their high
information capacity,
-
the
method of recording vibroacoustic signals enables quick measurements in natural
working conditions.
The
vibroacoustic signal is a complex signal coming from many sources. The
separation of the signal into individual components is possible when the
characteristic features of the signals generated by individual kinematic pairs
are known. The fundamental problems of vibroacoustic diagnostics include
finding a way to separate the signal into components that can be assigned to
specific sources, and establishing rules for assessing the state of a given
kinematic pair on the basis of the obtained signal. It is necessary to know the
characteristics of the vibroacoustic signal and its pre-processing methods.
Damage
symptoms obtained as a result of advanced vibroacoustic signal processing
methods can constitute patterns used during the construction of a diagnostic
system based on artificial intelligence methods.
2. EXAMPLES
OF VIBROACOUSTIC DIAGNOSTICS OF COMBUSTION ENGINE COMPONENTS IN A CAR
During the operation of technical devices, vibrations are generated, and the transmission center is the elements of the objects themselves and the environment in which they are located. This is the result of work processes taking place in the devices. The process of propagation of vibrations in any medium can be treated as a vibroacoustic process [6].
In a car, the biggest source of vibration and noise is the internal combustion engine. The sources of the forcing forces for these phenomena are:
-
combustion
processes,
-
fluctuations
in torque on the crankshaft,
-
movement
of components.
The occurring effects may be intensified by the occurrence of:
-
excessive
wear and damage of mating parts,
-
incorrect
balance (crankshaft, flywheel, camshaft, balance shaft),
-
loosening
of screw connections, mounting of the engine and its accessories,
-
damage to
the drive belt (V-belt, toothed),
-
worn or
damaged bearings,
- incorrect engine regulation.
It should be noted that the generation of vibroacoustic phenomena by working technical objects does not mean that they are in poor technical condition. A certain level will always occur and should be treated as nominal. Only the difference between the model of a machine that is working correctly or is in good technical condition and the actual case will indicate any damage to the components.
Difficulties in using vibroacoustic signals for diagnostic purposes result, among others, from the fact that they are generated simultaneously in different parts of the working machine. By receiving such signals from any places located on or around the object, one obtains at least the sum of the effects coming from such processes. The whole difficulty in determining the technical condition of the tested element lies in finding an appropriate measure that will be a clear symptom of the processes taking place in it. To make this possible, a method of processing the vibroacoustic signal must be developed in advance, which will allow extracting from the huge amount of information contained in the vibroacoustic signal only the information that corresponds to the information source related to a given element and its technical condition.
The vibroacoustic signal emitted by the vehicle's combustion engine can be represented as:
|
|
(1) |
where:
Ai, Bij(t) – amplitudes of signal components,
φi, φij – phases of signal components.
ωi, ωij – vibration frequencies of the signal components,
u(t) – impulse function,
tj – time defining the occurrence of an impulse phenomenon.
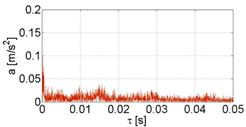
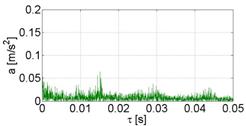
An example of vibration and acoustic signal recorded during operation of the vehicle's combustion engine is shown in Figure 1.
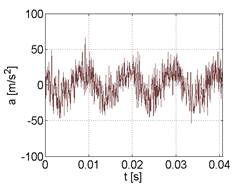
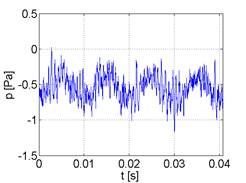
Fig. 1. Vibroacoustic signal emitted by the
vehicle's combustion engine:
(a) vibration signal, (b) acoustic signal
2.1. Analysis of
vibroacoustic signals in the time domain
Based on the image of the vibroacoustic signal in the time domain, it is possible to qualitatively assess the vibroacoustic process in terms of the degree of determinism, periodicity, occurrence or non-occurrence of certain parts of the process and their relationship with other events occurring in the object [5].
The time domain signal is most often characterized by amplitude measures. The measures used in diagnostics are:
-
mean
value (arithmetic mean):
|
|
(2) |
- effective value (standard deviation):
|
|
(3) |
- signal energy:
|
|
(4) |
- peak to peak value:
|
|
(5) |
- crest factor:
|
|
(6) |
- clearance factor:
|
|
(7) |
- shape factor:
|
|
(8) |
- impulse factor:
|
|
(9) |
- asymmetry coefficient:
|
|
(10) |
- clustering coefficient (kurtosis):
|
|
(11) |
- maximum value (quartile 4):
|
|
(12) |
- minimum value (quartile 0):
|
|
(13) |
- quartile 1: Q1,
-
quartile
2 (median): ![]() ,
,
-
quartile
3: ![]() ,
,
-
variance:
|
|
(14) |
- quartile deviation:
|
|
(15) |
- mean deviation:
|
|
(16) |
- geometric mean:
|
|
(17) |
- harmonic mean:
|
|
(18) |
- positional coefficient of variation:
|
|
(19) |
- coefficient of variation:
|
|
(20) |
- k-order central moment:
|
|
(21) |
where:
T – observation time,
N – number of samples.
The conducted research investigated the possibility of using amplitude measures determined on the basis of time-domain signals to diagnose ignition system failures manifested by the absence of a spark plug ignition spark.
The object of the research was a car with a combustion engine powered by petrol and LPG gas fuel. During the research, the angular position of the crankshaft and camshaft, the acceleration of vibrations of the engine body in the direction parallel and perpendicular to the cylinder axis and the acoustic pressure were recorded. The research was carried out for different engine speeds. The experiments were repeated with the engine running without damage and with no ignition spark in the first, second, third, fourth, first and fourth cylinders, and the second and third cylinders simultaneously.
The nature of changes occurring in the time domain of the recorded vibroacoustic signals was described using amplitude measures.
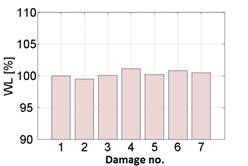
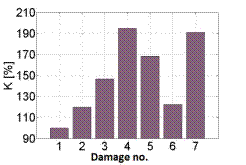
Figure 2 presents exemplary measures illustrating the changes in the nature of vibroacoustic signals in the time domain, described using measures that are sensitive and insensitive to a given type of combustion engine failure. In order to better illustrate the changes, the measures were presented on a percentage scale. It was assumed that 100 [%] corresponds to the value for no damage, while the remaining percentage values show how much the given measure changes in relation to a functional engine when simulated damage occurs.
Based on the research carried out, it can be concluded that using the diagnostic measures, it is only possible to recognize one of two engine operating states - lack of operation and failure in the form of failure to ignite in the cylinder. It can also be noticed that in the case of the engine fueled with LPG, the number of measures that can be used for diagnosis decreases.
2.2. Analysis of vibroacoustic signals in the
frequency domain
The main feature of signals, determined in the frequency domain, is the power spectral density. It is calculated using methods based on the Fourier transform. Machine diagnostics uses various Fourier transform methods, which allow obtaining amplitude, phase, and energy spectra [7].
The spectrum of the signal x(t) can be determined using the Fourier transform:
|
|
(22) |
|
a) |
b) |
|
|
|
Fig. 2. Measure insensitive (a) and sensitive
(b) to the type of fault
(1 - no fault; 2, 3, 4, 5 - no ignition spark in cylinder: 1, 2, 3, 4;
6, 7 - no ignition spark simultaneously in two cylinders: 2 and 3, or 1 and 4)
Fourier basis functions are well located in the frequency domain, which allows them to function as a basis for stationary, periodic signals, the description of which does not require the localization of harmonic components in time.
An important property of the Fourier transform is the preservation of energy invariance. The relationship between the energy of a signal in the time and frequency domains is defined by Parseval's theorem:
|
|
(23) |
In [4] a method of finding periodicity in a spectrum is presented. The procedure is called the multiplication spectrum and consists in determining the multiplication of successive harmonics in the spectrum range. The analyzed frequency fp is taken from a range limited to 1/3 of the entire spectrum range. The product spectrum can be determined from the relationship:
|
|
(24) |
where:
Guu – power spectral density,
fp – analyzed frequency ([Hz]),
k – subsequent harmonics.
A modification of this method is the polyharmonic spectrum determined from the relationship:
|
|
(25) |
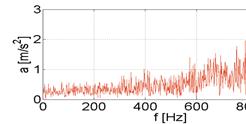
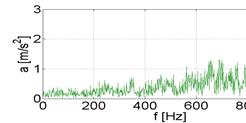
The tests carried out were aimed at assessing the wear of the piston-cylinder assembly using a vibration signal recorded on the body of a car's combustion engine. The signal of acceleration of the vibrations of the engine housing was measured in a direction perpendicular to the cylinder axis, with a sensor placed in the vicinity of the 4th cylinder. The tests recorded the vibration acceleration patterns of the engine body before and after repair. The engine repair consisted of replacing the worn pistons, which resulted in a reduction of the clearances in the piston-cylinder system.
In the next step, spectra were determined from the recorded accelerations of engine body vibrations. Example spectra determined from the engine vibration signal for two different states are shown in Figure 3.
|
a) |
b) |
|
|
|
Fig. 3. Spectrum of vibration accelerations
recorded on
the body before (a) and after (b) engine repair
The analysis of the obtained data shows that for the assessment of the wear of the piston-cylinder system, it is advisable to analyze signals in selected representative frequency ranges. Therefore, in the next step of the pattern construction process, the obtained spectrum range was divided into 40 sub-ranges - each of 500 [Hz].
In order to describe the nature of the spectrum changes, a histogram was determined separately for each sub-range. The limits of the histogram ranges were assumed by dividing the spectrum amplitude range into five equal parts, determined to the maximum value occurring in a given sub-range.
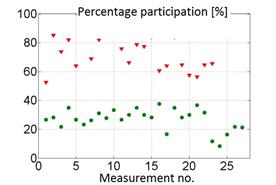
The next step in the pattern building process was to select only those ranges of the spectrum amplitude (range 1÷5) and only those sub-ranges of the spectrum (sub-range 1÷40) for which the separation of classes corresponding to worn and new pistons was visible. The results obtained for the example combination of the sub-range of the spectrum and the range of the histogram for correct and incorrect separation of classes are shown in Figure 4.
2.3. Cepstrum analysis in vibroacoustic diagnostics
A vibroacoustic signal can be represented as a product of two or more component signals. One way to separate the convolution components is to use homomorphic deconvolution in the form of cepstrum analysis [5].
|
a) |
b) |
|
|
|
Fig. 4. Example of a spectral subrange and
histogram range for correct (a) and incorrect (b) separation of the wear
classes of the piston-cylinder assembly
(▼ –
engine before repair, • – engine after repair)
In cepstrum analysis, the frequency domain is treated as if it were the time domain – and vice versa.
The real cepstrum can be defined as:
|
|
(26) |
where:
τ – quefrency about the dimension of time ([s]).
The argument of the cepstrum τ is not treated as dynamic time, nor as a delay time as in the correlation function. The occurrence of components for time τ in the cepstrum should be understood as a periodic component with frequency f=1/τ.
The tests carried out tried to assess the wear of the piston-cylinder assembly using the vibration signal recorded on the body of a car's internal combustion engine. From the recorded vibration accelerations of the engine housing, a cepstrum was determined.
Figure 5 shows an example of a cepstrum determined from the engine vibration signal for two different states.
|
a) |
b) |
|
|
|
Fig. 5. Cepstrum of vibration accelerations
recorded on
the body before (a) and after (b) engine repair
The research shows that for the assessment of the wear of the piston-cylinder system, it is advisable to analyze signals in selected representative frequency ranges. Therefore, in the next step of the pattern construction process, the obtained cepstrum range was divided into 5 sub-ranges – 0 to 0.01 [s], 0.01 to 0.02 [s], 0.02 to 0.03 [s], 0.03 to 0.04 [s], 0.04 to 0.05 [s].
In order to describe the nature of cepstrum changes for each sub-range, a histogram was determined separately. The limits of the histogram ranges were assumed by dividing the cepstrum amplitude range into five equal parts, determined by the maximum value occurring in a given sub-range. Based on preliminary experiments, it was found that better results are obtained by taking the value of the maximum cepstrum amplitude range separately for signals recorded before and after engine repair, rather than the range determined on the basis of all recorded signals both before and after repair.
Then, from all the cepstrum amplitude ranges (range 1÷5) and cepstrum sub-ranges (sub-range I÷V), only those were selected that allowed for visible separation of classes corresponding to worn and new pistons. Figure 6 shows an example of the cepstrum sub-range and histogram range for correct and incorrect separation of classes.
2.4. Analysis of vibroacoustic signals in the
time-frequency domain
In diagnosing early stages of damage, the basic problem is to find low-energy information concerning nonlinear effects, such as amplitude-phase modulations of the vibroacoustic signal. Therefore, typical spectral analysis, which is effective in considering boundary states, turns out to be of little use in this case [8].
The classical Fourier analysis method is not used to study non-stationary processes. The Fourier transform is used for frequency analysis of vibroacoustic signals determined over the entire time interval. However, it is often necessary to analyze local properties of signals by observing changes in the spectrum over time. In such cases, the analyzed signal x(t) is multiplied by functions related to the division of the analyzed time period into segments. The advantage of such a procedure is the possibility of spectral analysis of a selected signal slice. The analysis that allows such a procedure is called the short-time Fourier transform (STFT). The result of the transform depends not only on the signal itself, but also on the function of the cutting window [9].
The introduction of a window function in the time domain causes oscillations in the frequency domain, which is equivalent to the occurrence of information distortion disturbing the reconstruction of the tested signal.
If the window is shifted in the time domain by a smaller value than its size, subsequent data segments overlap. However, if the window shift value is larger than its size, not all signal fragments will be analyzed [10].
The short-time Fourier transform can be determined from the relationship:
|
|
(27) |
where:
b – shifting the window in the time domain,
f – analyzing frequency ([Hz]).
|
a) |
b) |
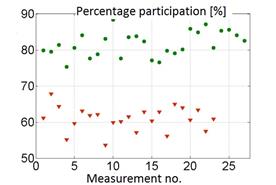
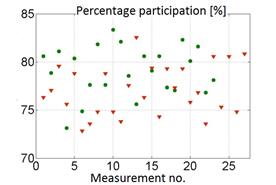 Fig. 6. Example of the cepstrum subrange and histogram range for
correct (a) and incorrect (b) separation of the wear classes of the
piston-cylinder assembly
Fig. 6. Example of the cepstrum subrange and histogram range for
correct (a) and incorrect (b) separation of the wear classes of the
piston-cylinder assembly
(▼ –
engine before repair, • – engine after repair)
The biggest disadvantage of this method is the constant, once selected, width of the notch window. Using a window of constant width is not very effective in the analysis of signals containing both low and high-frequency components. It limits the simultaneous precision in the time domain and the frequency range of the analysis. Narrowing the time interval, by using a narrow window, improves the time resolution of the spectrum, but at the same time worsens the accuracy in the frequency domain. A wide window provides high resolution in the frequency domain, but lower in the time domain. According to the uncertainty principle, the window has a constant area regardless of the transformation.
Another method of signal analysis that allows for obtaining a distribution in the time and frequency domain is the Wigner-Ville transform (WVD). It allows for analyzing the distributions of vibroacoustic signals – especially non-stationary signals – in the time-frequency coordinate system. This transform does not use any basis functions, and can be determined from the relationship:
|
|
(28) |
where:
x^* (t) – imaginary signal conjugate to x(t).
The pseudo Wigner-Ville transform has practical applications. In this transform, the function under the integral is multiplied by the window function w(t).
|
|
(29) |
where:
x^* (t) – imaginary signal conjugate to x(t),
w(t) – weighting function, similar to the time window used in STFT analysis.
The distributions obtained in this way are characterized by very good resolution in both the time and frequency domains. A characteristic feature is the lack of resolution limitations in both the time and frequency domains [11].
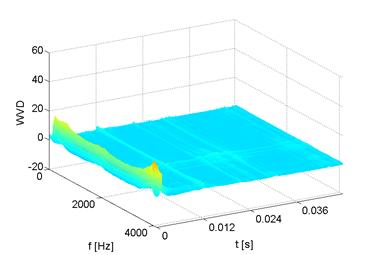
In the experiment, attempts were made to detect leaks in the intake system of a car's combustion engine using the accompanying vibrations. Damage to the system was simulated by leaking the intake manifold behind the throttle valve. This was achieved by using a precise needle valve with a micrometer screw. Four different valve positions were used.
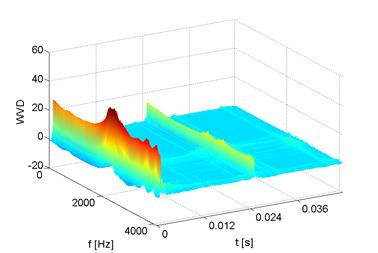
Time-frequency distributions were created from the recorded signals using the Wigner-Ville transform (WVD). The resulting Wigner-Ville distributions are shown in Figure 7.
In order to describe the nature of changes in the WVD distribution depending on the degree of damage, a two-stage procedure was adopted. In the I stage, statistical measures were determined for subsequent frequencies. The usability of 36 estimates, which are widely described in the literature, was checked. This procedure was aimed at describing the nature of changes in the time domain for subsequent frequencies determined in accordance with the assumed sampling frequency. In stage II, ranges of 500 or 1000 [Hz] length were extracted from the frequency characteristics obtained in this way. The purpose of division into ranges of different length variants was to check the effect of their size on the classification result. In each of the separated parts of the spectra obtained in this way, the nature of the distribution variability was described using 36 measures.
A vector consisting of a designated measure in each part of the spectrum constituted input data for a neural network classifier belonging to the group of artificial intelligence tools.
The experiment attempted to classify two states of the intake system of a combustion engine – the intake system in good condition and the presence of leaks.
Regardless of the choice of the vibration signal recording direction and the method of dividing the spectrum into ranges of different widths, for most cases used in stage II of the measures, a similar level of damage classification accuracy was obtained. The best results obtained were at the level of 10 [%] of classification error.
2.5. Application of higher order methods in
vibroacoustic diagnostics
In vibroacoustic diagnostics, there are cases when the power spectra of signals, time-frequency distributions, correlation analyses do not allow for the identification of changes occurring in non-stationary signals. An example of such changes are phase changes. In this case, higher-order moments and cumulants and their spectra may prove useful [12].
Higher-order cumulants are measures of the amount of change in a signal around its mean. They have the ability to expose the occurrence of nonlinearities in the signal [13].
Cumulants are related to statistical moments by the following relations:
|
|
(30) |
|
|
(31) |
|
|
(32) |
|
|
(33) |
|
a) |
|
|
|
b) |
|
|
Fig. 7. Wigner-Ville distribution in the
absence and occurrence of leaks in
the intake system of an internal combustion engine
In vibroacoustic diagnostics, the bispectrum is particularly used. In this analysis, the third-order cumulant is used, described by the relationship:
|
|
(34) |
where:
E() – expected value.
Applying the Fourier transform to the third-order cumulant allows us to determine the third-order power density spectrum with two independent frequencies:
|
|
(35) |
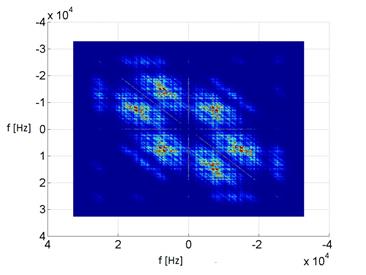
The experiment was conducted to check whether it is possible to diagnose leaks in the exhaust system of a car's internal combustion engine based on bispectrum analysis. The leak was modeled as damage to the exhaust valve head.
Bispectrum distributions were determined based on the recorded vibration signals, examples of which are shown in Figure 8.
The diagnostic method adopted in the experiment was based on comparing diagonal vectors of the bispectrum matrix. The obtained frequency characteristics were subjected to selection by separating frequency ranges of three widths - 1000 [Hz], 3000 [Hz], 5000 [Hz]. The adoption of ranges of different widths in the experiment was aimed at examining the effect of this parameter on the correctness of diagnostic information. A measure describing the nature of the distribution amplitude variability was determined from each spectrum range. 36 measures were used. A vector consisting of a designated measure in each selected part of the distribution was used as input data for a neural network classifier, which is a tool belonging to artificial intelligence methods.
The experiment attempted to build classifiers diagnosing the occurrence of a fault based on signals recorded at a given engine speed operating in a specific gear.
The obtained results indicate the possibility of building neural networks classifiers that work flawlessly.
2.6. The use of wavelet transform in vibroacoustic
diagnostics
Wavelet analysis makes it possible to linearly decompose the tested vibroacoustic signal using any basis function with a finite and short interval in which it assumes values other than zero. Wavelets are sign-variable functions, the value of which differs from zero in a narrow interval [14]. Local properties can only be well represented by functions that quickly decay to zero. The basic wavelet contains most of its energy in a certain frequency interval. Changing the frequency band of the wavelet is realized by changing the scale value. For the basic wavelet, increasing the scale will cause a decrease in the center frequency of the band-pass filter through the wavelet. At the same time, the width of the wavelet's frequency band will decrease, which is equivalent to increasing the resolution in the frequency domain.
Based on the basic wavelet, it is possible to generate a whole family of wavelets. This can be done using the formula:
|
|
(36) |
where:
a – scale value,
b – shift value,
t – time.
The undoubted advantages of this method include the losslessness of the transformation. This means that all energy is conserved when the signal passes from the time domain to the wavelet coefficients. This is defined as the principle of conservation of signal energy during the wavelet transformation - decomposition and reconstruction. This rule says that the entire signal energy, in the form of the sum of the squares of the values of all samples, equals the sum of the squares of all wavelet coefficients.
|
a) |
|
|
|
b) |
|
|
Fig. 8. Bispectrum distribution for a good engine and one with a fault in the exhaust system
In the literature, one can find descriptions of various forms of wavelet transform. One of them is the continuous wavelet transform (CWT) defined as:
|
|
(37) |
where:
ψ((t-b)/a) – wavelet transform basis function,
a – scale parameter related to location in the frequency domain,
aϵR^+, a≠0,
b – time domain shift parameter, bϵR.
The wavelet frequency is adjusted using the scale parameter a, while the parameter b can be used to study local properties of time courses. Adjusting the window width to the analyzed frequency range allows for studying non-stationary signals. For slowly varying waveforms, the window expands in the time domain, while at high frequencies it narrows, maintaining a constant surface area [15].
CWT analysis is a compromise in terms of time-frequency localization, which determines its usefulness in examining both polyharmonic and random signals (stationary or non-stationary). Matching the width of the analysis window to its average frequency unifies the uncertainty of the wavelet coefficient estimation in the entire distribution region.
The advantages of the wavelet transform allow for the simultaneous identification of components resulting from the occurrence of phenomena of various durations [16].
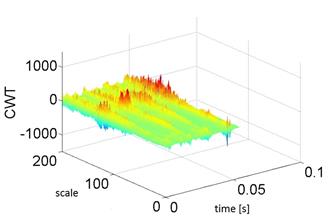
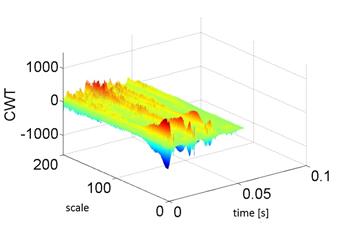
The aim of the experiment was to attempt to diagnose operational wear of the piston-cylinder assembly in a car's combustion engine. The experiment used recorded acceleration signals of the engine body vibrations in the direction perpendicular and parallel to the cylinder axis. In the conducted experiments, it was decided to check the usefulness of the continuous wavelet transform (CWT).
Examples of the distribution of recorded vibration signals resulting from the use of wavelet analysis are shown in Figure 9.
One of the possible ways to describe wavelet distributions are Hoelder coefficients, also known as Lipschitz coefficients. According to the literature [18], the relationship describing the CWT distribution can be transformed into the form:
|
|
(78) |
where:
a – scale parameter related to location in the frequency domain,
b – time domain shift parameter,
hH – Hoelder's coefficient,
CH – Hoelder's constant.
The next step in the process of determining the Hoelder coefficients was to adopt a scale range in which it would be possible to clearly separate different states of wear of the piston-cylinder assembly. The obtained CWT distributions did not allow determining the appropriate scale range. Because the experiment did not produce the desired results, an additional attempt was made, in which the scheme was modified to obtain Hoelder coefficients. Instead of determining the moment in the time domain for which a significant increase in the wavelet coefficient values is observed, the sum over time of wavelet coefficients for subsequent scale values was adopted for further steps.
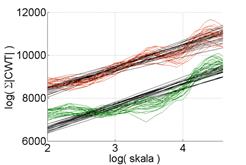
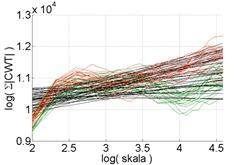
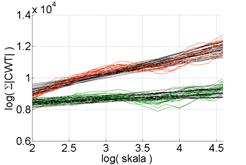
The obtained characteristics show a much more ordered character of amplitude changes than those determined earlier. A more detailed analysis of the results made it possible to determine the range of the scale for vibration acceleration signals perpendicular to the 4th cylinder and parallel to the 1st cylinder, in which two states of wear of the piston-cylinder assembly can be clearly separated. Only in the case of signals recorded in the direction parallel to the 4th cylinder, it was not possible to determine such a range. The determined distributions are shown in Figure 10.
|
a) |
|
|
|
b) |
|
|
Fig. 9. Distributions of the continuous wavelet transform of accelerations of vibrations perpendicular to this cylinder recorded before (a) and after (b) engine repair
3. CONCLUSIONS
Nowadays, we can observe a revolution
in the technologies related to motor vehicles. It can significantly improve
safety and reduce the risk of road accidents and limit the degradation of the
natural environment. Today's cars have become modern platforms, on board of
which increasingly advanced electronic systems are installed, which have a
direct impact on safety in the vehicle and outside it. Particularly important
are those technologies that, through their operation, have an impact on
reducing the negative effects of civilization development. The next step in the
ongoing revolution may be the introduction of new generations of active
intelligent systems that will be able to independently process vehicle
parameters, and thus affect the safety and health of all road users.
The article proposes the use
of vibroacoustic signals as a source of information about the technical
condition of the tested object, such as a car. This assumption is consistent
with the thesis that the best diagnostic methods are those that allow testing
objects without interfering with their operation. Any interference in the
operation of the facility will certainly result in false information about the
malfunction.
Direct use of recorded
vibration or acoustic signals does not provide a correct answer about the technical
condition. As studies show, for this purpose, it is necessary to properly
process the recorded vibroacoustic signal. This can be done using a whole range
of different types of methods. Based on them, you can build stand-alone
diagnostic measures or use such information as a basis for diagnostic systems
based on artificial intelligence methods.
|
a) |
b) |
|
|
|
|
c) |
|
|
|
|
Fig. 10. Distributions of Σ|CWT| within the adopted scale for vibration accelerations (a) perpendicular to the 4th cylinder, (b) parallel to the 4th cylinder, (c) parallel to the 1st cylinder, recorded before and after the engine repair
References
1.
Ziakopoulos A., G.
Yannis. 2020. „A review
of spatial approaches in road safety”. Accident Analysis & Prevention
135: 105323.
2.
Faus M., F. Alonso, E. Egido, M. Rezapour. 2023. „Editorial: Human factors in
transport and road safety”. Frontiers in Psychology 14: 1175488.
3.
Cociu S., Deleu R., Rimis C., Cebanu S., Cherecheș
R.M. 2022. „Ethical
Aspects in Road Traffic Safety and Driving Behavior Change”. Journal of
Intercultural Management and Ethics 5(1): 57-69.
4.
Cempel
C.: Vibroacoustic diagnosis of machines.
Warsaw: PWN. 1989.
5.
Cempel
C. 1998. „Vibroacoustical diagnostics of machinery: An outline”. Mechanical Systems and Signal Processing
2(2): 135-151.
6.
Randall
R.B., J. Antoni. 2011. „Rolling element bearing diagnostics – A tutorial”. Mechanical Systems and Signal Processing
25: 485-520.
7.
Nawrocki
W., R. Stryjski, M. Kostrzewski, W. Woźniak, T. Jachowicz. 2023. „Application
of the vibro-acoustic signal to evaluate wear in the spindle bearings of
machining centres. In-service diagnostics in the automotive industry”. Journal of Manufacturing Processes 92:
165-178.
8.
Shabbir
N., L. Kütt, B. Asad, M. Jawad, M.N. Iqbal, K. Daniel. 2021. „Spectrum analysis
for condition monitoring and fault diagnosis of ventilation motor: a case
study”. Energies 14(7): 2001.
9.
Yang Y., Z. Peng, W. Zhang, G. Meng. 2019. „Parameterised time-frequency
analysis methods and their engineering applications: A review of recent
advances“. Mechanical Systems and Signal
Processing 119: 182-221.
10.
Li
X., X. Liu, C. Yue, S.Y. Liang, L. Wang. 2022. „Systematic review on tool
breakage monitoring techniques in machining operations”. International Journal of Machine Tools and Manufacture 176: 103882.
11.
Gade S., K. Gram-Hansen. 1996. „Non-stationary signal analysis using
wavelet transform, short-time Fourier transform and Wigner-Ville distribution”.
Rewiev 2. Bruel & Kjær.
12.
Nikias
L.C., M.J. Mendel. 1993. „Signal processing with high-order spectra”. IEEE Signal Processing Magazine July
1993: 10-37.
13.
Jasinski
M., S. Radkowski. 2011. „Use of the higher spectra in the low-amplitude fatigue
testing”. Mechanical Systems and Signal
Processing 25(2): 704-716.
14.
Korbicz
J., Z. Kowalczuk, J.M. Kościelny, W. Cholewa. 2012. Fault Diagnosis: Models, Artificial Intelligence, Applications.
Berlin, Heidelberg: Springer.
15.
Batko
W., M. Ziółko. 2002. Application of
wavelet theory in technical diagnostics. Cracow: AGH Publishing House.
16.
Manarikkal I., F. Elasha, D. Mba. 2021. „Diagnostics and prognostics of
planetary gearbox using CWT, auto regression (AR) and K-means algorithm”. Applied Acoustics 184: 108314.
17.
Loutridis
S., E. Douka, A. Trochidis. 2004. „Crack identification in double-cracked beams
using wavelet analysis”. Journal of Sound
and Vibration 277: 1025-1039.
Received 02.10.2024; accepted in revised form 29.11.2024
![]()
Scientific
Journal of Silesian University of Technology. Series Transport is licensed
under a Creative Commons Attribution 4.0 International License