Article citation information:
Danchuk, V., Hutarevych, O. Adaptable dynamic routing system in urban transport logistics problems using GIS data. Scientific Journal of Silesian University of Technology. Series Transport. 2024, 125, 19-31. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2024.125.2.
Viktor DANCHUK[1],
Oleksandr HUTAREVYCH[2]
ADAPTABLE
DYNAMIC ROUTING SYSTEM IN URBAN TRANSPORT LOGISTICS PROBLEMS USING GIS DATA
Summary. To solve the problems
of online route optimization in urban transport logistics, an adaptive dynamic
routing system based on GIS data is proposed. Here, it is possible to
simultaneously take into account the actual configuration of the urban road
network (URN) and the real-time dynamics of traffic flows. Route optimization
is performed on a weighted bidirectional graph for an asymmetric dynamic
traveling salesman problem using a modified ant colony optimization algorithm.
The system allows automatically updating the weights of the graph depending on
the current changes in the characteristics traffic in the URN sections,
obtained from GIS data, and fixing the optimal configuration of a partially
completed route before updating the graph. To test the proposed system, the
simulation of dynamic routing processes was conducted in real-time, using the
delivery of goods to Żabka grocery stores in Warsaw as an example. The results
indicate the proposed method’s feasibility for solving practical urban
transport logistics management problems under complex traffic.
Keywords: intelligent transportation systems, AI
optimization methods, information technology, geographic information systems,
transport logistics
1. INTRODUCTION
One of the most critical ways to enhance the efficiency of urban transport logistics is by improving the productivity of freight delivery processes through route planning and optimization. Given the dynamic nature of urban road networks (URN), the practical solution to such problems lies in employing innovative dynamic routing technologies that operate in real-time, leveraging advanced software, timely acquisition, and transmission of primary URN state data, and fast intelligent discrete route optimization methods.
Despite advances, the development of
effective dynamic routing systems remains a challenge. Real-time data
acquisition about URN states (traffic characteristics, weather conditions,
vehicle technical specifications, etc.) has improved with modern motion sensors
and GPS systems. However, the development and application of intelligent route
optimization methods, particularly for complex delivery point configurations
such as the traveling salesman problem (TSP), are often limited to simulation
studies on model examples without considering real traffic conditions on URN
sections.
This paper presents the development
results of a dynamic routing system for goods delivery within the dynamic TSP
(DTSP), utilizing GIS data on current traffic conditions in URN sections. The
route optimization is performed using a modified ant colony optimization
algorithm (ACOmod). The study results on dynamic
routing, using a section of the Warsaw URN as an example, demonstrate the
proposed method’s potential for solving practical transport and logistics
management problems in complex traffic conditions.
2. LITERATURE REVIEW AND PROBLEM STATEMENT
Currently, the problem of Vehicle Routing (VRP) in transportation logistics is often formulated as a generalized Traveling Salesman Problem (TSP) [1]. In this context, the TSP involves finding a set of optimal routes for visiting a given set of nodes with a specified number of vehicles based at a depot so that each node is typically visited once. Therefore, the aim is to minimize the total cost of the route. The TSP is often represented as either a directed or bidirectional graph with a static or dynamic set of vertices (nodes) connected by edges (arcs) with defined weights. Based on these weights, a corresponding cost matrix is constructed and analyzed. The costs may include distances between delivery points, travel time, fuel consumption, trip expenses, etc. [1].
Depending on the nature of the
evolution of input data, VRP can be classified into two main categories: static
VRP (SVRP), where input data is known in advance and remains unchanged, and
dynamic VRP (DVRP), where input data changes over time [1]. Until recently,
routing and planning problems in transport-logistics systems were mainly solved
using methods for SVRP (see, for example, [2]). In these cases,
transport-logistics operations were carried out with fixed or minimally
variable system characteristics during service time [2].
Solving urban transport logistics
issues is possible within the DVRP approach, which must account for variable
factors related to time and service changes during transit. This requires
modern innovative online dynamic routing technologies that contain appropriate
software, systems for timely acquisition data of URN state, as well as fast
intelligent methods for routes discrete optimization [3].
The rapid development of intelligent
transportation systems (ITS) over the past decade has sparked significant
interest in solving DVRP routing problems among researchers. This interest is
related to the development and application of innovative technologies for
acquisition and processing data, as well as the development of modern methods
of intelligent solutions within the framework of ITS.
In particular, GPS integrated to modern geographic information systems (GIS), the Internet of Things (IoT), blockchain (BC), big data (BD), and modern information and communication technologies enables automated dynamic routing through real-time data integration. This includes tracking vehicle movements and changes in customer requests, traffic updates, information exchange among participants in the transport process, weather forecasting, etc. [4]. Modern examples of such devices include GPS trackers, traffic sensors (often digital cameras), weather sensors, mobile applications, etc. [5].
As the analysis shows, until
recently, significant attention has been devoted to using GIS data for dynamic
routing problems, mainly without considering traffic updates on network
segments during vehicle movement [6–9]. For example, in [6], dynamic route
planning in logistics for urban public sports facilities is studied based on
GIS and Multi-agent systems. In [7], using ArcGIS software with network analyst
extensions and regression analysis, a set of the fastest delivery routes for
fresh vegetables was determined. In [8], a cluster method for flexible routing
was presented, incorporating GIS and discrete-event simulation. Here, results
of optimal delivery route forecasting (including time and distance) for
variable freight delivery addresses and reverse trip pickups were provided. In
[9], a platform offering an efficient solution for CVRP and GVRP routing tasks
was proposed, employing a K-means algorithm to dynamically define different
geographical delivery zones and plan routes considering current traffic GIS
data. These studies typically leverage GIS’s advantages by using data about the
real configuration of the transport network segments connecting any two nodes,
as well as relevant attributes (speed limits, traffic jams, intersection
waiting times, real-time traffic data, etc.). Here, route optimization is
mainly performed using classic discrete optimization methods for small-sized
transport-logistics problems.
In recent years, the papers with
using of traffic data on URN sections obtained through different types of
traffic sensors have been less represented in literature compared to one with
GIS data. Depending on the chosen measurement technology, this may be primarily
due to high costs, significant installation and maintenance expenses, limited
coverage radius, etc. For example, in [10], an intelligent system for real-time
trip optimization was developed using machine learning based on traffic data
from 52 sensors placed on California highways. In [11], results of simulation
modelling using real-time VANET (Vehicular Ad hoc NETwork) traffic data and
simulators such as OmNet++ (network communication simulator) and SUMO (urban
mobility simulator) for traffic light management processes to form optimal
route sets for travelers were presented.
Now, heuristic or metaheuristic
methods, typically based on artificial intelligence (AI), as well as their
modifications, and hybrids, are using in ITS to ensure high-speed solutions for
large-scale DVRP discrete optimization problems. It should be noted that DVRP
is an NP-hard problem, with computation time increasing significantly as the
number of nodes grows. Therefore, most developments and research on AI methods
for DVRP discrete optimization have so far focused on reducing computation time
and finding the global minimum during optimization [12]. In this case, as a
rule, a model representation of the URN is considered in the form of a graph
for a certain number of nodes with variable arc weights, which, at best,
correspond to the average values of the parameters of the dynamics of traffic
flows on URN sections or to extreme cases (for example, traffic jams) at a
certain point in time [13]. Most dynamic routing solutions are simulated
on model examples without considering the actual URN state and configuration.
As analysis shows, a significant
number of works within the DVRP framework focus on solving problems for vehicle
routing with dynamic time windows (DVRPTW) and variable demands (VRPVD). For
instance, in [14], a hybrid ant colony algorithm is used to study a
multi-objective vehicle routing problem with flexible time windows, integrating
road costs, fixed vehicle usage costs for delivery, and penalty costs incurred
for early or late service into a single objective function. In [15], DVRPTW was
solved as a multi-time window problem within a sliding horizon using heuristic
optimization methods. It should also be noted that to solve multi-parametric
problems (variable time windows, customer demands, etc.), hybrid algorithms
combining AI-based discrete optimization methods with artificial neural
networks (ANN) of machine learning are often used [16]. Here, ANN is employed
either for forecasting specific transport processes or for tuning heuristic
parameters of intelligent optimization methods under changing environmental
conditions.
AI methods for solving DVRP for
large-scale dynamic TSP (DTSP), considering real-time ITS traffic data, are
currently imperfect, far from practical application, and require further
development. For example, in [17], DVRP was carried out within DTSP using
various AI methods and historical ITS data on transport flow dynamics. Here, it
was also shown that one of the most effective algorithms for solving such
problems is the Ant Colony Optimization (ACO). It was found to have better
optimization effects for DVRP within DTSP (shorter time and higher solution
accuracy) compared to, for example, ESA and GA [17]. Additionally, ACO and most
of its modifications are more versatile, allowing routing problems on URN for
both small and large-scale DTSP [17]. In [18], DTSP is used as a basic task for
creating dynamic test cases, considering two types of DTSP: (a) changes in the
number of nodes and (b) changes in edge weights. Population-based ACOs
utilizing pheromone evaporation and memory archives for adaptation to dynamic
changes are applied to enhance DTSP performance [18]. In [19], a dynamic ACO
(DAACO) was proposed to improve global minimum finding efficiency,
incorporating two enhanced strategies: a convex hull initialization strategy
and K-means clustering, as well as a local search strategy between two
neighbors. Experimental results indicate that the proposed algorithm
outperforms modern DFACO and DEACO algorithms [19].
In [20], simulation modelling of
time-based discrete route optimization with dynamic updating of client visit
sequences during movement was conducted for the first time. Here, traffic
sensor information was used both in real-time and as averaged historical
traffic data. However, in [20], route optimization was performed using a
spreadsheet solver with open-source software for VRP, and computational
operations for route optimization were excessively slow, preventing full
real-time mode implementation [20].
Therefore, this study aims to
develop an adaptable dynamic routing system for freight delivery within the
DTSP framework, utilizing GIS traffic data for route discrete optimization with
AI method. Here, the use of GIS traffic data is essential for considering the
actual URN configuration and real traffic dynamics. To ensure high performance
and adaptability in route optimization with dynamic updates under
non-stationary traffic conditions, a ACOmod is proposed.
3. METHODOLOGY
This study examines the asymmetric
dynamic traveling salesman problem (DTSP) as a weighted bidirectional graph in
the context of the urban road network (URN). The graph consists of nodes (0, …, n-1) with
respective Cartesian coordinates, where each node represents a delivery point,
and node 0 is the depot. In this study, the number of nodes is fixed. Each edge
of the graph is composed of a set of URN sections that represent the optimal
route between each pair of nodes,
as determined by GIS data. The attributes of the graph’s edges include the
travel time and length of these section sets, corresponding to the optimal
route between the nodes.
The weight of each edge is determined by a function based on the attributes of
the URN section sets, travel time, and the total length of these URN sections.
Depending on the optimization criteria, the optimization procedure focuses on
corresponding attributes of this function.
An adaptable dynamic routing system
for freight delivery is defined as a system designed for real-time route
re-optimization in response to changes in the URN state due to traffic flow
dynamics on its sections during freight transport [1].
The proposed method involves three
main stages for the functioning of the adaptable route optimization system in
the asymmetric DTSP using ACOmod :
· Building the initial graph for the URN’s initial state and constructing the
optimal route for this graph.
· Dynamically updating the graph according to changes in road conditions
(traffic flow dynamics, congestion, accidents, temporary road closures, etc.).
· Optimizing the route on the updated graph.
GIS data on the current traffic
conditions on URN sections are used to account for the actual URN
configuration. This data is obtained using the Routes API of the Bing Maps
service (GIS developed by Microsoft) [21]. This service finds the most optimal
route between two points, specified by coordinates or addresses, and provides
discrete characteristics such as route time and length, considering the current
load of URN sections, accidents, temporary closures, etc.
Thus, the graph construction uses
optimal routes obtained from real-time GIS data to connect each pair of
delivery points. The constructed graph models the DTSP for the current state of
the URN section, considering its actual configuration and traffic flow
dynamics. The route optimization or re-optimization process for the constructed
or updated graph is then performed based on real-time traffic data provided by
the Bing Maps Routes API, which includes current changes in traffic dynamics on
URN sections.
To provide high performance and
adaptability of the route optimization process with the possibility of dynamic
updates under non-stationary traffic conditions, a modified ant colony
optimization algorithm ACOmod is proposed (see Figure 1).
In this ACOmod,
the weights of the graph are automatically updated based on changes in dynamic
characteristics on URN sections, while fixing the optimal configuration of a
partially completed route before updating the graph. The algorithm for fixing
the optimal configuration of a partially completed route is described as
follows:
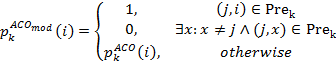(1)
According to (1), fixing the optimal
configuration of a partially completed route involves adding partially defined
optimal routes to the memory of the ants. The ACOmod
algorithm introduces 
– a list of graph edges that ant k must follow within the optimal configuration of the partially
completed route, ignoring the probabilistic rule 
of the classic ant colony algorithm described
in [22]. Thus, when at node j=Pos(k) in the graph, ant k moves to node i if 
;
otherwise, the next node is determined by the classic probabilistic rule (see Figure 1 and (1)). The second condition
in (1) describes the list of graph edges that do not belong to the partially
completed optimal route.
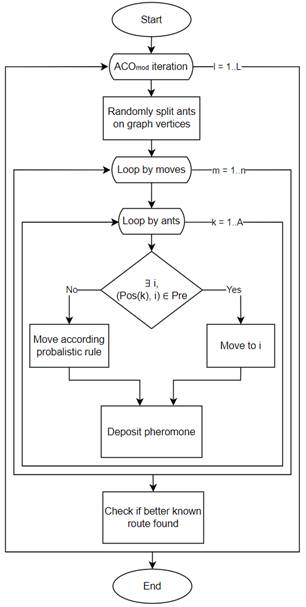
Fig. 1. Block diagram of the proposed modified
ant colony optimization algorithm ACOmod
The
general scheme of the adaptable dynamic routing system for freight delivery
within the DTSP framework using GIS data is shown in Figure 2.
As shown in Figure 2, the system operates as follows: The user inputs the initial data into the system, including the starting point (depot), delivery points, and the route optimization criterion. The user also configures route update triggers, which are events that initiate graph rebuilding according to the current situation and find the optimal route on the updated graph. Triggers can be events caused by manual user interaction with the system (Manual trigger), events when the vehicle arrives at a delivery point (Arrival trigger), or events occurring according to a user-defined schedule (Schedule trigger), such as route updates every 5 minutes. The system allows multiple triggers to operate simultaneously.
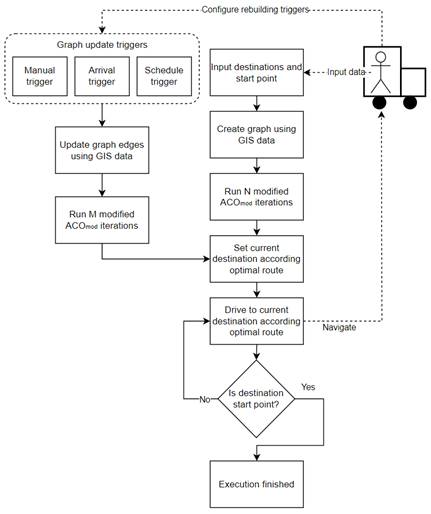
Fig. 2. Flowchart of the proposed adaptable
dynamic routing system of freight delivery within the framework of the DTSP
task using GIS data
According to Figure 2, at time 
, before the vehicle departs from
the initial point 
(depot), a graph 
corresponding to the current state of the URN
at time is formed based on GIS data. By performing
N iterations using ACOmod, the optimal freight delivery route
in the DTSP is found according to the specified criterion:
.
(2)
In (2) 
is the sequence of graph edges that corresponds to the optimal route
configuration at time ; , 
, … , 
(), …, 
are the delivery nodes corresponding to the
optimal route configuration at time ; 
, …, 
are variables determining the order of passing
the graph nodes for the optimal route configuration at time
After optimization procedure on the
graph , the first edge 
in the optimal route sequence : (
is fixed. This means that during subsequent
route re-optimization at future times 
, the edge (
will be included in the optimal solution
according to (1).
Upon the vehicle’s arrival at
delivery point 
at time 
, the graph 
corresponding to the URN state at time is updated using the Bing Maps Routes API in
response to the arrival trigger event. The optimal freight delivery route in
the DTSP is then found according to the specified criterion:
(3)
by performing M iterations using ACOmod. In (3) , , 
, … , 
, … , 
are the delivery nodes corresponding to the optimal route configuration
at time . The next edge 
in the optimal route 
is then fixed: 
. Subsequent route re-optimization
follows the described update algorithm, fixing the corresponding route edges
optimized in previous stages.
If a route update trigger (see
Figure 2) activates while the vehicle is moving, such as a schedule trigger
event, the system updates the graph according to the current URN state and
finds the optimal route by performing M iterations using ACOmod. However, it is assumed that the vehicle has
already arrived at point 
to avoid introducing new intermediate nodes
representing the vehicle’s current position during optimization.
4.1. Case Study: Goods Delivery to Żabka
Grocery Stores in Warsaw
The proposed dynamic routing system in DTSP using the ACOmod and GIS data was tested on a fragment of Warsaw’s URN. In this task, 10 Żabka grocery stores were considered, with their locations specified by addresses. The graphical representation of the delivery points and the current state of the URN is shown in Figure 3. These stores were selected based on the following assumptions:
·
The depot is
located at point n=0 (Krucza 46, 00-509 Warsaw, Poland).
·
The delivery route
type is circular, with sequential delivery of goods.
·
The date and time
of delivery are considered, but unloading time at delivery points,
nomenclature, mass, and volume of the ordered goods are not considered.
·
In each set of URN
sections corresponding to a particular graph edge, there will always be
alternative routes.
·
Changes in average
travel time mainly depend on changes in traffic flow dynamics, including stops
or delays due to traffic signals, congestion, and other traffic complications
affecting vehicle speed on URN sections.
A basic implementation of the proposed system was developed on the .NET 6 platform using C#. The research was conducted on an Intel Core i5-8400 CPU @ 2.80GHz with 16 GB DDR3 RAM and Windows 10 OS. The studies showed that building a graph with 10 nodes or updating it according to the current URN state took an average of 5.37 seconds, while finding the optimal solution for a graph with 10 nodes using 1000 iterations of ACOmod took an average of 926ms. The graph construction/update speed was limited by the service limits of the Routes API for the developer license. Performance could be significantly improved with production-level license.
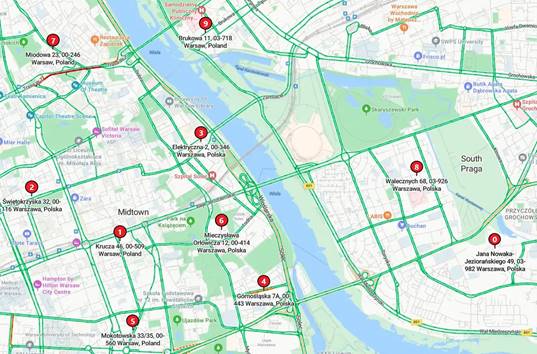
Fig. 3. Locations of the depot (n=0) and
delivery points (n=1, …, 9) (Żabka grocery stores) on the map of Warsaw
[21]
4.2. Routing in DTSP with Dynamic Updating of the Optimal Route During Goods
Delivery Using GIS Data
In the DTSP task, for a vehicle
departing from store 0 (depot) at = 03.07.2024 at 17:45:00 UTC +1, the
optimal time route for delivering goods to all other stores and returning to
store 0 (depot) needs to be found, considering current URN state changes due to
non-stationary traffic flow dynamics on URN sections. As an example, the
studies were conducted with dynamic graph updates using a Schedule trigger
regime (see Figure 2) with a 5-minute update frequency via the Bing Maps
service. Route re-optimization occurred at the moments of the vehicle’s arrival
at the respective delivery points according to the Schedule trigger event
algorithm (see Figure 2).
Table 1 presents the routing results
with dynamic optimization of the delivery route to Żabka grocery stores in
Warsaw. Column 1 shows the vehicle’s arrival/departure time at/from the
respective delivery point according to the assumptions in this work (see
Section 3). Column 2 shows the sequence of delivery points for the optimal
route based on re-optimization results according to the Schedule trigger event
algorithm (see Figure 2, Section 3). Here, red indicates visited nodes,
blue indicates the next node based on re-optimization results, and gray
highlights the part of the optimal route rebuilt due to re-optimization
compared to the initial (planned) optimal route. Column 3 contains the time (in
seconds) for the route optimized at previous stages before the vehicle’s
arrival at the respective point (see (3) Section 3). Column 4 contains the
expected time (in seconds) to complete the remaining route based on
re-optimization results according to the current URN state at the time of route
re-optimization at the respective delivery point. Column 5 shows the time of
the last graph update according to the Schedule trigger event algorithm at the
time of route re-optimization based on GIS data at the respective delivery
point.
Tab.
1
Routing
results with dynamic route optimization for goods delivery to Żabka grocery
stores in Warsaw using GIS data on 03.07.2024
|
Arrival / departure time |
Sequence of visits
with dynamic route optimization |
Time of optimal route |
URN state per
Schedule trigger |
||
|
From start (s) |
Expected to finish (s) |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
17:45:00 |
0->8->6->3->9->7->2->1->5->4->0 |
0 |
4327 |
17:45:00 |
|
|
17:52:27 |
0->8->6->3->9->7->2->1->5->4->0 |
447 |
3751 |
17:50:00 |
|
|
18:01:36 |
0->8->6->4->5->1->2->7->3->9->0 |
996 |
3295 |
18:00:00 |
|
|
18:05:27 |
0->8->6->4->5->1->2->7->3->9->0 |
1227 |
3101 |
18:05:00 |
|
|
18:10:16 |
0->8->6->4->5->1->2->7->3->9->0 |
1516 |
2808 |
18:10:00 |
|
|
18:14:25 |
0->8->6->4->5->1->2->7->3->9->0 |
1765 |
2559 |
18:10:00 |
|
|
18:20:40 |
0->8->6->4->5->1->2->7->3->9->0 |
2140 |
2170 |
18:20:00 |
|
|
18:28:58 |
0->8->6->4->5->1->2->7->9->3->0 |
2638 |
1614 |
18:25:00 |
|
|
18:36:38 |
0->8->6->4->5->1->2->7->9->3->0 |
3098 |
1153 |
18:35:00 |
|
|
18:44:28 |
0->8->6->4->5->1->2->7->9->3->0 |
3568 |
662 |
18:40:00 |
|
|
18:55:30 |
0->8->6->4->5->1->2->7->9->3->0 |
4230 |
0 |
18:55:00 |
|
As Table 1, the studies revealed
that significant traffic redistribution on URN sections can lead to substantial
route adjustments. For instance, at 18:01:36, re-optimization for the current
URN state at 18:00:00 resulted in rebuilding the optimal route
(0->8->6->4->5->1->2->7->3->9->0) compared to the
initial (planned) optimal route (0->8->6->3->9->7->2->1->5->4->0)
when vehicle departs from the depot at 17:45:00 (see Table 1). In addition, at
18:28:58, re-optimization during the vehicle’s stay at point 9 led to partial
route reconstruction from 3->9->0 to 9->3->0. Thus, at the
vehicle’s return to the depot at 18:55:30, the optimal route was
0->8->6->4->5->1->2->7->9->3->0, differing from
the initial optimal route at 17:45:00
(0->8->6->3->9->7->2->1->5->4->0). The travel
time was reduced to 4230 seconds compared to the planned 4327 seconds (see
Table 1).
5. CONCLUSIONS
This work proposes, for the first
time, an adaptable dynamic routing system for urban transport logistics,
enabling the simultaneous consideration of the actual configuration of the
urban road network (URN) and the real-time dynamics of traffic flows on its
sections during goods transportation. The optimization process was carried out
within the framework of an asymmetric DTSP on a weighted bidirectional graph.
The dynamic route optimization procedure during goods delivery is executed
using a modified ant colony optimization algorithm ACOmod.
Within the developed ACOmod, the graph weights are
automatically updated based on current changes in the dynamic characteristics
of URN sections, obtained via the Bing Maps Routes API. Additionally, the
system ensures the fixation of the optimal configuration of the partially
completed route before graph updating.
To validate the proposed system,
comprehensive simulations of dynamic routing processes were conducted online,
using time as the optimization criterion, exemplified by goods delivery within
the DTSP framework to Żabka grocery stores in Warsaw. The study results
demonstrate the potential of the proposed method for solving practical urban
transport logistics management problems under complex traffic conditions.
References
1.
Pop Petrică C., Ovidiu Cosma, Cosmin Sabo, Corina
Pop Sitar. 2024. „A
comprehensive survey on the generalized traveling salesman problem”. European
Journal of Operational Research 314(3): 819-835. DOI: https://doi.org/10.1016/j.ejor.2023.07.022.
2.
Thompson
Russell G., Lele Zhang. 2018. „Optimizing
courier routes in central city areas”. Transportation Research Part C:
Emerging Technology 93: 1-12. DOI: https://doi.org/10.1016/j.trc.2018.05.016.
3.
Schroten Arno, Anouk Van Grinsven, Eric Tol, Louis
Leestemaker, Peter-Paul, et al. Research for TRAN Committee – The impact of
emerging technologies on the transport system, European Parliament, Policy
Department for Structural and Cohesion Policies, Brussels. ISBN
978-92-846-7392-6.
4.
Darvishan Ayda, Gino J. Lim. 2021. „Dynamic network flow optimization for
real-time evacuation reroute planning under multiple road disruptions”. Reliability
Engineering & System Safety 214:107644. DOI: https://doi.org/10.1016/j.ress.2021.107644.
5.
Zantalis Fotios, Grigorios Koulouras, Sotiris
Karabetsos, Dionisis Kandris. 2019. „A Review
of Machine Learning and IoT in Smart Transportation”. Future Internet
11(4): 94. DOI: https://doi.org/10.3390/fi11040094.
6.
Yuan Jixue, Jun Song, Yuwen Zhang, Chaozhe
Jiang, Fang Xu. 2013. „Planning
of Dynamic Routing of Logistics in Urban Public Sports Facilities Based on
MAS”. ICTE 2013 - Proceedings of the
4th International Conference on Transportation Engineering: 1156-1162. 19-20 October 2013. Chengdu,
China. DOI: https://doi.org/10.1061/9780784413159.168.
7.
Abousaeidi Mohammad,
Rosmadi Fauzi, Rusnah Muhamad. 2015. „Geographic Information System (GIS) modeling
approach to determine the fastest delivery routes”. Saudi Journal of Biological
Sciences 23(5): 555-564. DOI: https://doi.org/10.1016/j.sjbs.2015.06.004.
8.
Lyu Zichong, Dirk
Pons, Yilei Zhang, Zuzhen Ji. 2021. „Freight operations modelling for urban delivery and
pickup with flexible routing: cluster transport modelling incorporating
discrete-event simulation and GIS”. Infrastructures 6(12): 180. DOI: https://doi.org/10.3390/infrastructures6120180.
9.
Tsoukas Vasileios, Eleni Boumpa,Vasileios
Chioktour, Maria Kalafati, Georgios Spathoulas, Athanasios Kakarountas.
2023. „Development of
a dynamically adaptable routing system for data analytics insights in logistic
services”. Analytics 2(2): 328-345. DOI: https://doi.org/10.3390/analytics2020018.
10.
Park Jungme, Yi Lu Murphey, Ryan McGee,
Jóhannes G. Kristinsson, Ming L. Kuang, Anthony M. Phillips. 2014. „Intelligent trip modeling for the prediction of
an origin–destination traveling speed profile”. IEEE Transactions on
Intelligent Transportation Systems 15(3): 1039-1053. DOI: https://doi.org/10.1109/TITS.2013.2294934.
11.
Chai Huajun, H.M. Zhang, Dipak Ghosal,
Chen-Nee Chuah. 2017. „Dynamic
traffic routing in a network with adaptive signal control”. Transportation
Research Part C: Emerging Technologies 85: 64-85. DOI: https://doi.org/10.1016/j.trc.2017.08.017.
12.
Ng Kam K.H., C.K.M. Lee, S.Z. Zhang, Kan Wu,
William Ho. 2017. „A multiple colonies
artificial bee colony algorithm for a capacitated vehicle routing problem and
re-routing strategies under time-dependent traffic congestion”. Computers
& Industrial Engineering 109: 151-168. DOI: https://doi.org/10.1016/j.cie.2017.05.004.
13. Zajkani M.A., R. Rahimi Baghdorani, M. Haeri. 2021. „Model predictive based approach to solve DVRP with traffic congestion”. IFAC-PapersOnLine 54(21): 163-167. DOI: https://doi.org/10.1016/j.ifacol.2021.12.028.
14. Zhang Huizhen, Qinwan Zhang, Liang Ma, Ziying Zhang, Yun Liu. 2019. „A hybrid ant colony optimization algorithm for a multi-objective vehicle routing problem with flexible time windows”. Information Sciences 490: 166-190. DOI: https://doi.org/10.1016/j.ins.2019.03.070.
15.
Hoogeboom Maaike, Wout Dullaert. 2019. „Vehicle routing with
arrival time diversification”. European Journal of Operational Research
275(1): 93-107. DOI: https://doi.org/10.1016/j.ejor.2018.11.020.
16. Yu Xu. 2022. „Logistics distribution for path optimization using artificial neural network and decision support system”. Research Square: 1-17. DOI: https://doi.org/10.21203/rs.3.rs-1249887/v1.
17. Zhang Ning. 2018. „Smart logistics path for cyber-physical systems with Internet of Things”. IEEE 6: 70808-70819. DOI: https://doi.org/10.1109/ACCESS.2018.2879966.
18.
Mavrovouniotis
Michalis, Maria N. Anastasiadou, Diofantos Hadjimitsis. 2023. „Measuring the performance
of ant colony optimization algorithms for the dynamic traveling salesman problem”.
Algorithms 16(12): 545. DOI: https://doi.org/10.3390/a16120545.
19.
Liu Huijun, Ao Lee,
Wenshi Lee, Ping Guo. 2023. „DAACO: adaptive dynamic quantity of ant ACO
algorithm to solve the traveling salesman problem”. Complex &
Intelligent Systems 9: 4317-4330. DOI: https://doi.org/10.1007/s40747-022-00949-6.
20.
Russo Francesco,
Antonio Comi. 2021. „Sustainable urban delivery: the learning process of
path costs enhanced by information and communication technologies”. Sustainability
13(23): 1-17. DOI: https://doi.org/10.3390/su132313103.
21.
Microsoft Learn.
“Bing Maps Routes API”. Available at: https://learn.microsoft.com/en-us/bingmaps/rest-services/routes/.
22. Dorigo Marco, Mauro Birattari, Thomas Stutzle. 2006. „Ant colony optimization”. IEEE Computational Intelligence Magazine 1(4): 28-39. DOI: https://doi.org/10.1109/MCI.2006.329691.
Received 25.07.2024; accepted in revised form
15.10.2024
Scientific
Journal of Silesian University of Technology. Series Transport is licensed
under a Creative Commons Attribution 4.0 International License