Article citation information:

Sistuk, V. A comparative study of headway-based and transport system-based assignments of public transport in Visum: the city of Kryvyi Rih case. Scientific Journal of Silesian University of Technology. Series Transport. 2024, 124, 171-182. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2024.124.12.

Volodymyr SISTUK[1]

A COMPARATIVE STUDY OF HEADWAY-BASED AND TRANSPORT SYSTEM-BASED ASSIGNMENTS OF PUBLIC TRANSPORT IN VISUM: THE CITY OF KRYVYI RIH CASE

Summary. Many researchers have explored public transport assignment methodologies employing transport modelling software. Nevertheless, there remains a gap in evaluating real-world public transit networks utilizing diverse assignment procedures within Visum software. This paper introduces a thorough comparison of algorithms involved in public transport assignment processes, using the transport model of the city of Kryvyi Rih in Ukraine. The three scenarios of the model were developed depending on the public transport assignment procedure: headway-based, transport system-based utilized to all links, turns, and major turns in the network graph, and transport system-based applied only to the links, turns, and major turns traversed by the active public transport lines. The model of the network comprises 13 transport systems, 7 transport modes, 27598 links, 10097 nodes, 83270 turns, 238 zones, 1748 connections for private transport, 3013 connections for public transport, 534 stops, 1165 stop areas, 1190 stop points, 130 lines and 218 line routes. The transport demand model encompassed 14 demand segments. Compared to the outputs of the model calculation using the headway-based procedure, in the scenarios with transport system-based assignment, passenger flows on rail tram lines significantly decreased. Also, the results of scenarios with transport system-based assignment showed that the passengers extremely use parallel streets for travel from an origin to a destination. The modelling outputs for an actual urban network illustrate that the choice of the shortest route in the transport system-based assignment is closely linked to the main urban roads. This circumstance could potentially result in a rise in the number of transfers needed to sustain accessibility to districts residing far from the central highway.

Keywords: transport modelling, public transport, headway-based assignment, transport system-based assignment, impedance, demand model, Visum

1. INTRODUCTION

For many years, development of a new urban passenger transport (PuT) network and improving existing ones has been a significant concern. The success of these efforts relies heavily on the expertise of transport modellers and the resources at their disposal [1]. The task involves analysing modelling outcomes, which necessitates a proficient transport modeller. The modeller interprets the results, typically employing a graph-based analytical approach, and devises customized solutions for optimizing the network. In essence, the process of optimizing and routing PuT is carried out manually by the modeller. Additionally, guidance from transportation macro-modelling manuals [2, 3, 4], various analytical methods [5], and heuristic algorithms [6, 7, 8] are utilized in developing new routes for PuT networks. It is also possible to optimize the existing network using meta-heuristic methods, such as the genetic algorithm [7], or the ant colony algorithm [8], which is applied to urban transport models [8]. The reliability indicators can act as indicators to gauge the effectiveness of the measures taken to optimize the transport network [9].

In [6], an effort was made to bridge the gap between theoretical exploration of the urban transit routing problem (UTRP) and practical transport planning, utilizing the Visum software as a research tool. A procedure was devised to automate the problem-solving concerning the optimal PuT routing, which involved extracting connectors between PuT stops from the Visum model using a Python script and the Visum COM-API. This process generated a UTRP graph with an undirected list of stops. Subsequently, this graph was optimized using a hyper-heuristic algorithm, and the adjusted routes (oriented stop lists) were converted into PuT routes in Visum for assessment. The criteria for optimizing the PuT route network on a global scale included both passenger and operator total costs. The outcomes of the global optimization indicated the effectiveness of the hyper-heuristic algorithm for networks of various sizes, from small to large cities.

The algorithms mentioned above for PuT routing and optimization entail either: a) optimizing routes for networks with indirect connections, which are not reliant on transport macro-modelling software, or b) intricate transition processes between software environments and the UTRP interface. These aspects render these algorithms rather complex for practical implementation in transport models of real cities, which often comprise numerous links, nodes, zones, and demand segments. As a result, there are significant gaps between the theoretical approaches to determining the best routing for PuT networks and the actual implementation of applicable algorithms in real-world transport planning practices [6].

Meanwhile, procedures for PuT demand assignment within transport modelling software incorporate the utilization of shortest path-search algorithms, which are based on customizable criteria. Essentially, optimal routing algorithms are inherently integrated into the mathematical network, often utilizing implicitly derived indicators. Consequently, conducting a comparative analysis of modelling outcomes using various PuT assignment procedures becomes essential. These assignment results can then be effectively employed to optimize existing networks and/or develop new ones.

Many researchers have studied the PuT assignment procedures [10-19]. Paper [12] introduces a strategy for addressing the challenge of PuT distribution, focusing on networks characterized by line routes with headway- and schedule-based traffic patterns. The mathematical model is tested on the example of the Copenhagen metropolis. Paper [13] presents an approach to the use of agent-based modelling for PuT assignment. In the context of assessing the PuT demand, work [14] modelled the distribution of passenger traffic on bus routes using the Simulation of Urban Mobility (SUMO) software. In [15], a model was developed to analyse the distribution of passenger flows along bus lines based on headway, considering uncertainty in the impedance function. Additionally, the Method of Successive Averages (MSA) was introduced.

Study [16] presents the development of an integrated multimodal model for mode choice and PuT assignment, which allows users to combine passenger transport on predefined routes (Fixed PT) and on-demand transport (Flexible PT) in such a way as to minimize travel costs. In a PuT system, the vehicle fleet is managed by a central control centre, which allocates incoming transportation requests among vehicles in real time. The authors of [17] used the Connection Scan Algorithm to model PuT assignment, in which passengers choose a line route based on travel time, number of transfers, walking time, waiting time, and delays. Paper [18] presents the results of model PuT assignment based on timetables (logistic regression to describe the assignment of passenger flows was applied) using the Visum software on the example of sparsely populated regions in the Republic of Lithuania.

Despite numerous studies on modelling urban PuT networks, including those utilizing specialized software, there has been a lack of assessment of real PuT networks using various assignment procedures within the Visum software.

Given the information provided, the objectives of this study are as follows:

- conducting a comprehensive comparison of algorithms involved in the processes of PuT assignment within the Visum software;

- modelling an actual PuT network in Visum, employing various assignment procedures (illustrated with the city of Kryvyi Rih, Ukraine as an example);

- analysing the outcomes of PuT modelling concerning different assignment procedures.

2. MATERIALS AND METHODS

In the classical transport model, the PuT assignment procedure, along with private transport (PrT) assignment, constitutes the fourth and final stage. This stage follows the trip generation, distribution, and mode choice. Previously, the Visum software [10] offered transport planners two procedures for PuT assignment demand: line-based (based on average headway) and schedule-based. Assignment based on the average headway involved considering the sequence of PuT stops and travel time between them, as well as the headways on the line route. The route assessment considered the perceived journey time (PJT). The timetable-based assignment already considered, in addition to PJT, the passenger's utility of a particular departure time for choosing the shortest route between two transport areas in the network. The latter variant of the assignment procedure is typically used for rail and bus networks with long headways (more than 15 minutes) and strict adherence to the schedule.

In addition to the previously mentioned procedures for the PuT assignment, modern versions of the Visum software also incorporate assignments based on a transport system (Tsys-based). Transport systems encompass various individual transport vehicles such as cars and motorcycles, as well as the vehicles of PuT like buses, trams, trolleybuses, metros, and taxis. This procedure is often employed for schematic planning of PuT lines within an “ideal” network.

Using the Tsys-based PuT assignment procedure allows for preliminary planning of lines, considering both the existing network and hypothetical PuT lines independently. By comparing the modelling outcomes obtained from the Tsys-based procedure with those from the “basic” assignment procedure used in the transport model, conclusions can be drawn regarding the alignment of the existing transport network with its idealized concept.

For instance, Kryvyi Rih exemplifies a city profoundly influenced by open pit mining activities, including iron ore open pits and tailings dumps, which significantly shape the city's master plan. For Kryvyi Rih, the primary assignment procedure for PuT modelling is the Headway-based procedure (HB). This preference stems from the fact that up to 65% of passenger traffic within the city relies on private bus routes, operating at intervals of up to 30 minutes.

Accordingly, the task that is relevant today is to compare the Tsys-based and HB assignment algorithms to use their advantages in optimizing the passenger transport network.

2.1. Transport system-based assignment

The procedure calculates the shortest routes (minimum required time), which are then compared with the demand for transportation. The obtained passenger flows represent the “preferred route network” for the users.

PuT lines are not affected by the Tsys-based assignment. The modelling of transport supply only considers links of the basic network with specific travel times.

There are three possible methods for determining the shortest route [4]:

- considering all links (connections), turns, and main turns within the network graph (road and rail connections);

- considering links, turns, and main turns used by PuT lines;

- considering links, turns, and main turns utilized by active PuT lines.

The Tsys-based assignment defines a particular route to every combination of origin and destination areas. This route includes an origin connection, a destination connection, and the permissible links and turns for the specified transport system. For each pair of origin and destination, the lowest impedance is calculated for the available links, turns, and connections within the transport system, utilizing the associated function.

(1)

where RT is the ride time on the link, TP is the “transfer penalty” when changing the transport system, nTP is the “transfer penalty” for a specific type of node.

In the search for the shortest path, transfer times between PuT stops are not considered because specific PuT lines are not differentiated. Transfers are simply viewed as a switch between different transport systems. In the impendance function, transfers are regarded as a time “penalty” during path searching, occurring only at specific nodes. The total transfer time comprises a penalty for a particular node type and an additional penalty for the transfer itself.

Links that are accessible to multiple PuT systems with varying travel durations have their minimum ride time established. The total demand for a specific origin-destination pair is then assigned to the route with the least impedance. Consequently, each passenger selects the route with the shortest travel duration, irrespective of the existing PuT network or schedules.

The Tsys-based assignment exhibits the following characteristics [4]:

- it disregards PuT frequency and waiting times for transfers;

- frequent transfers between different transport systems are common;

- the travel time between two parallel routes within the same transport system is averaged;

- journey times can only be estimated when there are short PuT headways;

- the number of transfers and the time spent during transfers cannot be estimated.

The developer of the Visum software recommends the procedure of Tsys-based assignment as an effective method for elaborating the model of a new route network. However, the Visum user manual [4] underscores that this procedure cannot entirely substitute timetable or HB assignments.

2.2. Headway-based assignment

The HB PuT assignment procedure includes three operational steps.

1. Calculation of the headway of the line.

2. Search and select a line.

3. Loading the line.

The line headway calculation can be performed by the software in several ways:

a) from the user-defined attribute of the time profile on the line route;

b) from the average value of the headway according to the schedule on the line route;

c) from the average waiting time according to the line route schedule.

For the third case, if the set of departure times on the line T_l = {y₁, y₂, …, y_n} in the time interval l=[a, b], the first departure after time b is denoted as y'. We also consider a fictitious departure when the interval is extended by l in the form of the dependence y'' = y₁ + (b-a). To calculate the waiting time at the end of period l, we use the departure {y', y''}. The interval is calculated according to the formula [4]:

(2)

where is defined by for all i ∈ {1, ..., n-1}.

The search and choice of a route (line) in the HB procedure consists of two stages:

- routes are evaluated in terms of their impedance (total cost);

- a choice model is used based on logistic regression.

The impedance function includes the perceived journey time (PJT) and a component that considers the fare or the share of fare points.

(3)

where IMP is the indicator of an impedance, PJT is perceived journey time, α, β – coefficients, FP – fare.

The impedance function is determined using the following equation:

(4)

where IVT is the time spent in the vehicle, RIT is the travel time between the initial and final stops, ACT is the walking time to the initial stop, EGT is the walking time from the stop to the final destination, WKT is the total walking time, OWT is the waiting time at the first stop, TWT is the waiting time for a transfer, NTR is the number of transfers, λ1 - λ8 are the coefficients of the impedance function.

Tab. 1 presents a comparison of the PJT components for which appropriate skim matrices can be calculated for Tsys-based and HB assignments [4]. The main distinction between the two procedures, as indicated in Tab. 1, lies in the inclusion of waiting time at the initial stop and transfer duration within the HB assignment method.

Tab. 1

Skims of time in PuT assignment procedures

Outcomes	Notation	Procedure
		Tsys-based	Headway-based
Journey ride time	JRT	+	+
Ride time	RIT	+	+
In-vehicle time	IVT	+	+
Run time with PuT Aux transport systems	AXT	+	+
Origin wait time	OWT	-	+
Weighted origin wait time	WOWT	-	+
Transfer wait time	TWT	-	+
Weighted transfer wait time	WTWT		+
Access time	ACT	+	+
Egress time	EGT	+	+
Walk time	WKT	+	+

In the transport model of the city of Kryvyi Rih, the PJT parameter of impedance is as follows:

(5)

When HB assignment is used, the decision model for passengers choosing to board a vehicle assumes that their behaviour is influenced by the information accessible to them. The software provides four distinct models of passenger awareness, as described in references [4, 19]:

- No information, where headways on routes adhere to an exponential distribution law.

- No information but with constant headways on the lines.

- Information available regarding waiting time.

- Information available on the next departure time from the line stop.

In this paper, we consider the second option as the one that best reflects the state of awareness of users of the passenger transport system in Kryvyi Rih.

Let the set of available PuT lines be given by M = {1, ..., n}. Each line i ∈ M is characterized by a specific travel time t_i ≥ 0 and a travel interval h_i > 0. The frequency of movement on the line is defined by λ_i=1/ h_i.

For simplicity, we further assume that the lines are sorted in ascending order according to the remaining travel time. Thus, the following expression applies t₁ ≤ t₂ ≤ ... ≤ t_n. The set of i-th lines is encoded as follows: M_i = {1, ..., i}. The travel time t_i means the total cost of line i using, which includes the components of impedance.

Based on the available information, the choice model calculates the optimal set M*⊆ M_і and, for each line i ∈ M*, the demand shares d_i ≥ 0. The waiting time applied when choosing any network M' before boarding is denoted as W_L*, and the corresponding costs are obtained from the following equation:

(6)

These parameters are random variables, as they depend on the random arrival of vehicles at the stops. For the optimal set M*, the following condition is also satisfied with the corresponding probabilities:

P() ≤ P() (7)

for any value of M’⊆ M.

In the absence of information and a constant headway, a passenger chooses the line that arrives first from the optimal set of lines M* = M_i*.

The demand share for a particular line is determined by the expression:

(8)

where h^/= min {h_i} is the minimum headway, and w is the waiting time.

Hence, the probable waiting time is determined:

(9)

where i^* is the optimal line.

Since i^*= argmin_i{P}, the optimal route network consists of those lines that reduce the expected remaining cost.

Apart from the methods for PuT assignment, another crucial aspect in evaluating the performance of the urban passenger transport network is the calculation of PuT operating indicators. These indicators enable the analysis of network links or specific lines in attribute form.

3. RESULTS

The demand assignment for PuT was studied using a transport model of the city of Kryvyi Rih, which was developed in the Visum software.

The passenger transport model consists of a network model and a 4-step transport demand model. The network, in turn, includes 13 transport systems (bicycles, cars, buses, light (two-axle), medium (two-axle) and heavy (three-axle, long-haul) trucks, light rail, tram, trolleybus, taxi, suburban bus, pedestrian, pedestrian walking to PuT), 7 transport modes (bicycle, passenger car, light, medium and heavy truck, pedestrian and PuT), 27598 links, 10097 nodes, 83270 turns, 238 zones, 1748 connections for PrT, 3013 connections for PuT, 534 stops, 1165 stop areas, 1190 stop points, 130 lines and 218 line routes.

The transport model contains 14 demand segments according to different travel purposes. The sequence of calculation procedures included initialization, trip generation and attraction procedures, travel cost calculation, assignment of correspondences, mode selection, calculation of border area traffic, combination of correspondence matrices, PrT assignment, PuT assignment, blocking back model, and assignment analysis.

The travel costs between areas are computed by considering travel distance and the impedance value, which varies based on different time components for distinct transport modes. The distribution of correspondences across demand segments and the mode choice were conducted utilizing the Kirchhoff function. Within the passenger transport model, there are four modes, each associated with a distinct demand segment, resulting in the calculation of 56 matrices for mode choice.

The modelling of assignment in the transport system of Kryvyi Rih was carried out for one variant of the assignment procedure for PrT (the Bi-conjugate Frank Wolfe) and three variants of the assignment procedure for PuT.

The following procedures were employed for PuT assignment:

- HB approach - scenario 1.

- TSys-Based approach:

Applied to all links (connections), turns, and major turns in the network graph (including road and rail links) - scenario 2.

Applied only to the links, turns, and major turns traversed by the activated (existing) PuT lines - scenario 3.

Hence, the assessment was conducted across three assignment scenarios within the transportation system.

Comparing the passenger flow maps generated through HB PuT assignment (scenario 1) and TSys-based PuT assignment (scenario 2) across all links in the network graph, alongside TSys-based PuT assignment (scenario 3) for links with routes, enables us to pinpoint network sections exhibiting significant changes in the analysed indicator.

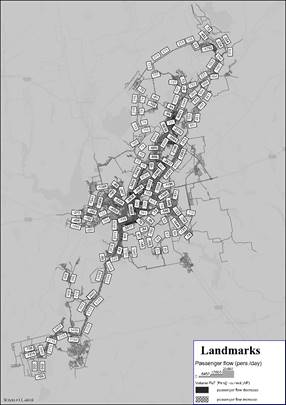
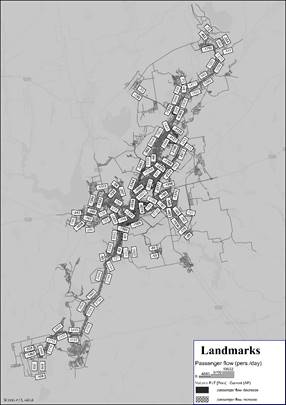
Here, an “increase in passenger traffic” refers to a rise in passenger flow observed with TSys-based assignment over HB (indicating positive values on the cartogram). Conversely, a “decrease in passenger traffic” denotes a decline in passenger flow observed with TSys-based assignment compared to HB (manifesting as negative values on the cartogram, see Fig. 1, Fig. 2).

Scenario 2, considering all links of the network graph to find the shortest route, is characterized by the following features in the formation of passenger flows on PuT:

- a new route with the shortest route between the southern and northern parts of the city is proposed along Het'mans'ka Street, where there is no PuT in the current situation;

- transport link between Metalurhiinyi and Dovhyntsivskyi districts is provided by a new section along Nikopolske shose Street;

- involvement of parallel streets (V. Gurova street) and bypass roads (Dovhyntsivskyi district) in the use of PuT;

- increase passenger traffic on the city's main streets in Saksahans'kyi and Pokrovskyi districts;

- decrease in passenger traffic on Universytets'kyi Avenue;

- increase in passenger traffic on Starovokzalna Street;

- increase in passenger traffic in the southern part of the city towards the geographically separated districts of Pivdennyi GZK and Inhulets'kyi district;

- decrease in passenger traffic on the high-speed tram lines.

Scenario 3, considering the existing passenger transport network, differs in the PuT flow distribution from scenario 2. The main differences between scenario 3 and scenario 1 are as follows. Reduced demand for PuT will be observed for the following streets: Ukrainska, Sviato-Mykolaivska, and Shyrokivska Streets, Kobylianskoho – Pisochna direction, Universytetskyi Avenue, Dniprovske Shose Street, Volonteriv Street and Spaska Street, S. Rziankina Street. The streets experiencing a decrease in demand for PuT include Kryvorizhstal Street, Metalurhiv Avenue, V. Gurova Street, Sobornosti Street, Kokchetavska Street, towards Pivdennii GZK and Inhulets'kyi district.

The following features are common to scenarios 2 and 3:

- a significant increase in passenger traffic on the central (main) streets of the city from south to north for Myru Avenue, V. Velykogo Street, 200th-richchia Kryvoho Rohu Avenue;

- decrease in passenger traffic on the streets of the historic part of the city such as Ukrainska, Svyato-Mykolaivska;

- increase in passenger traffic on Kobylianskoho Street towards Nikopolske Shose Street;

- decrease of passenger traffic on the main street of Universytetskyi Avenue and further along Dniprovske Shose Street;

- increase in passenger traffic on parallel streets in the Metalurhiinyi District;

- decrease in passenger traffic on the alternative route along Volonteriv Street, including the exit to the central highway;

- decrease in passenger traffic bypassing the central highway through the adjacent Zarichnyi and 129th neighbourhoods.

4. CONCLUSIONS

This study aimed to conduct a comparative analysis of modelling outcomes using different PuT assignment procedures in the Visum software, utilizing the transport model of the city of Kryvyi Rih as an example. In summary of the modelling results, the following conclusions can be drawn.

Fig. 1. The differences in the PuT passenger flow values obtained from TSys-based (scenario 2) and HB PuT assignment (scenario 1)	Fig. 2. The differences in the PuT passenger flow values obtained from TSys-based (scenario 3) and HB PuT assignment (scenario 1)

In the TSys-based PuT assignment, the demand for PuT is primarily concentrated along the main streets connecting various city districts from south to north. This shift prioritizes road transport over rail public transport, leading to decreased passenger flows on rail tram lines and their corresponding links in the network graph. Consequently, the significance of rail tram lines, serving as alternative routes in the historic city centre, diminishes. Notably, there is an increase in demand along the main streets leading towards the southern, isolated districts. Additionally, parallel streets see increased utilization, especially in areas with a nearly rectangular development layout. The connection between the central (Metalurhiinyi) and eastern districts (Dovhyntsivskyi) is established through the shortest route. Furthermore, employing the shortest path method implies that rather than circumventing high-rise neighbourhoods (Skhinyi-1, 2, 3), demand is anticipated for exit routes from these neighbourhoods. Alternative routes, like those through streets bypassing the central highway such as Volunteers Street, are largely disregarded. However, when PuT assignment considers all network links to find the shortest route, a notable difference in results emerges significant passenger flow is redirected from the central highway to a diagonal street, Het'mans'ka, which is frequently utilized by PrT along the south-north axis of the city.

Using TSys-based PuT assignment allows for estimating the transport supply possibilities with the existing demand for PuT without fully considering many existing constraints to explore alternative solutions in the network. This method is particularly valuable for sketch planning of new lines or routes. However, the results of the PuT assignment for a real urban network demonstrate that the choice of the shortest route in the TSys-based assignment, closely tied to the central highway, can detrimentally impact residents of districts distant from it in selecting alternative transportation options. This could lead to an increase in the number of transfers required to maintain accessibility to appropriate districts.

The utilization of the investigative approach delineated in this paper may represent an initial stride towards enhancing the PuT network through the employment of appropriate transport modelling software.

References

1. Jing Dian, Enjian Yao, Rongsheng Chen, Xun Sun. 2023. “Optimal Design Method of Public Transit Network Considering Transfer Efficiency.” IET Intelligent Transport Systems 17(6): 1118-36. DOI: https://doi.org/10.1049/itr2.12349.

2. 2024. Transport Analysis Guidance (TAG). TAG unit M3-2 public transport assignment modelling, including forthcoming changes for May 2024. Department for Transport.

3. 2014. JASPERS Appraisal Guidance (Transport). The Use of Transport Models in Transport Planning and Project Appraisal.

4. 2024. PTV VISUM User Manual. PTV Planung Transport Verkehr GmbH.

5. Farahani Reza Zanjirani, Elnaz Miandoabchi, W.Y. Szeto, Hannaneh Rashidi. 2013. “A Review of Urban Transportation Network Design Problems.” European Journal of Operational Research 229(2): 281-302. DOI: https://doi.org/10.1016/j.ejor.2013.01.001.

6. Soares Philipp Heyken, Leena Ahmed, Yong Mao, Christine L. Mumford. 2020. “Public Transport Network Optimisation in PTV Visum Using Selection Hyper-Heuristics.” Public Transport 13(1): 163-96. DOI: https://doi.org/10.1007/s12469-020-00249-7.

7. Soares Philipp Heyken. 2020. “Zone-Based Public Transport Route Optimisation in an Urban Network.” Public Transport 13(1): 197-231. DOI: https://doi.org/10.1007/s12469-020-00242-0.

8. Zhongyi Lin, Yang Cao, Huasheng Liu, Jin Li, and Shuzhi Zhao. 2021. “Research on Optimization of Urban Public Transport Network Based on Complex Network Theory.” Symmetry 13(12): 2436. DOI: https://doi.org/10.3390/sym13122436.

9. Cats Oded, Gert-Jaap Koppenol, Martijn Warnier. 2017. “Robustness Assessment of Link Capacity Reduction for Complex Networks: Application for Public Transport Systems.” Reliability Engineering & Safety System 167: 544-53. DOI: https://doi.org/10.1016/j.ress.2017.07.009.

10. Friedrich Markus, Thomas Haupt, Klaus Noekel. 1999. “Planning and Analyzing Transit Networks: An Integrated Approach Regarding Requirements of Passengers and Operators.” Journal of Public Transportation 2(4): 19-39. DOI: https://doi.org/10.5038/2375-0901.2.4.2.

11. Horbachov Peter, Oleksandr Makarichev, Olha Svichynska. 2022. “A New Route Choice Model for Urban Public Transit with Headway-Based Service.” Periodica Polytechnica Transportation Engineering 51(1): 22-30. DOI: https://doi.org/10.3311/pptr.15864.

12. Eltved Morten, Otto Anker Nielsen, Thomas Kjær Rasmussen. 2019. “An Assignment Model for Public Transport Networks with Both Schedule- and Frequency-Based Services.” EURO Journal on Transportation and Logistics 8(5): 769-93. DOI: https://doi.org/10.1007/s13676-019-00147-4.

13. Gentile Guido, Michael Florian, Younes Hamdouch, Oded Cats, Agostino Nuzzolo. 2016. “The Theory of Transit Assignment: Basic Modelling Frameworks.” Modelling Public Transport Passenger Flows in the Era of Intelligent Transport Systems 2016: 287-386. DOI: https://doi.org/10.1007/978-3-319-25082-3_6.

14. Orlando Victoria M., Enrique G. Baquela, Neila Bhouri, Pablo A. Lotito. 2022. “Analytical and Simulation-Based Estimation of Public Transport Demand.” Transportation Research Procedia 62: 727-34. DOI: https://doi.org/10.1016/j.trpro.2022.02.090.

15. Tan Qian, Xiangdong Zhou, Wusheng Liu. 2021. “Transit Assignment Modeling Approaches Based on Interval Uncertainty of Urban Public Transit Net Impedance.” Tehnicki vjesnik - Technical Gazette 28(5): 1582-1589. DOI: https://doi.org/10.17559/tv-20210520044802.

16. Narayan Jishnu, Oded Cats, Niels van Oort, Serge Hoogendoorn. 2020. “Integrated Route Choice and Assignment Model for Fixed and Flexible Public Transport Systems.” Transportation Research Part C: Emerging Technologies 115: 102631. DOI: https://doi.org/10.1016/j.trc.2020.102631.

17. Briem Lars, Sebastian Buck, Holger Ebhart, Nicolai Mallig, Ben Strasser, Peter Vortisch, Dorothea Wagner, Tobias Zündorf. 2017. “Efficient Traffic Assignment for Public Transit Networks.” In: 16th International Symposium on Experimental Algorithms (SEA 2017): 20:1-20:14. 2017.

18. Kieu Le Minh. 2011. „ Public transportation modeling in urban areas.” Master thesis. Norrkoping, Sweden: Linköping University.

19. Ranceva Justina, Rasa Ušpalytė-Vitkūnienė. 2024. “Specifics of Creating a Public Transport Demand Model for Low-Density Regions: Lithuanian Case.” Sustainability 16(4): 1412. DOI: https://doi.org/10.3390/su16041412.

20. Hildebrand Cisilia, Stina Hörtin. 2014. „A comparative study between Emme and Visum with respect to public transport assignment.” Master thesis. Linköping, Sweden: Linköping University.

Received 20.05.2024; accepted in revised form 20.07.2024

Scientific Journal of Silesian University of Technology. Series Transport is licensed under a Creative Commons Attribution 4.0 International License

---

[1] Faculty of Mechanical Engineering and Transport, Kryvyi Rih National University, Vitalii Matusevych Street, 11, Kryvyi Rih, Ukraine. Email: sistuk@knu.edu.ua. ORCID: https://orcid.org/0000-0003-4907-4265