Article citation information:
Matyja,
T., Stanik, Z. Simulation
tests of fleet vehicles periodic inspections timeliness: a case study. Scientific Journal of Silesian University of
Technology. Series Transport. 2022, 115,
75-91. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2022.115.6.
Tomasz MATYJA[1],
Zbigniew STANIK[2]
SIMULATION TESTS OF FLEET VEHICLES PERIODIC INSPECTIONS TIMELINESS: A
CASE STUDY
Summary. This study analyzed the case of a medium-sized workshop and the income
from servicing individual customers. The management of the company observed
some unused potential in the garage and plans to sign contracts with fleet
customers for comprehensive maintenance of their vehicles. The key question was
how many fleet vehicles could be additionally serviced without losing
individual customers? In this work, a simulation model of a workshop was
developed, treated as a system for queuing orders and vehicles. The model includes
a subsystem of random generation of fleet vehicle mileage during the
simulation. The idea of event-driven simulation and the Matlab/Simulink
SimEvent environment library was used.
Keywords: fleet
vehicles, periodic inspections, event-driven simulations
1. INTRODUCTION
Presently,
companies with fleets of vehicles rarely have their own technical facilities
that allow them to perform periodic inspections and repairs. It is common
practice to outsource this type of service and sign contracts with specialist
workshops [14, 17, 18]. When the fleet is unified in
terms of brand or the vehicles are leased, inspections are usually carried out
by authorized workshops of the vehicle manufacturer. Smaller companies with a
diverse fleet usually look for local universal workshops.
The issue of
periodic technical inspection is important in the case of fleet vehicles, as
they usually have daily mileage of hundreds of kilometers. Periodic inspections
are therefore performed very often, usually several times a year. Timely
performance of periodic technical inspections, consisting of the replacement of
fluids, filters, worn parts and visual inspection of the vehicle has a huge
impact on maintaining the good technical condition of the vehicle [11, 19].
This translates into a reduction in the failure rate of the equipment,
increasing road safety [9, 20]. It should also be mentioned here about the
possibility of using new non-invasive vehicle diagnostic methods [5-8].
The
relationship between a customer, his vehicle and the workshop can be described
through the queue theory using queues (FIFO and priority queues) and servers
imitating service work or waiting for a service [12, 24]. Most of the
parameters and state variables of the customer-vehicle-workshop system are
random. The mileage of vehicles based on which decisions on the inspection are
made increases randomly. The events taking place in the system are also random,
for example, issuing an order for a service or starting and ending a service.
The assessment of the quality of the client-vehicle-workshop system operation
can be obtained by the Monte Carlo method [16] by randomly generating events
and observing the behavior of the system and the average values of state
variables.
The described
problem can be modeled using the event-driven simulation method [3, 4, 23]. Event-driven simulation methods are commonly used to
solve tasks related to broadly understood customer service [2]. Many available
computer programs enable this type of simulation [1, 10, 13, 15, 21]. The chosen tool for this work was the SimEvent library of the Matlab/Simulink
environment [22, 25]. The choice of the modeling tool was determined by the
high flexibility of the Matlab language, which
significantly facilitated the programming of the elements of the
customer-vehicle-workshop system, the creation of which is not supported by the
SimEvent library itself.
The model of
workshop operation developed by the authors, together with the simulation of
fleet mileage, will be used to assess the workshop's potential in the field of
technical inspections and repairs. The use of queuing theory elements and
event-driven simulations in modeling the elements of the queue allows creating
a realistic environment reflecting reality. The conducted simulation tests make
it possible to detect any unfavorable phenomena in the operation of the
workshop, for example, in the form of blockages and critical delays in the
provision of services. The research will also make it possible to make the most
favorable decisions for the company.
2. FORMULATING THE DECISION PROBLEM
This
study examines the case of a medium-sized workshop that currently serves only
individual customers. In the near future, signing contracts with fleet
customers for comprehensive vehicle maintenance is being considered. Such a
step would primarily provide the company with a steady stream of orders for its
services, and also enable the plant to maximize its current unused capacity.
Based
on the company's history, it can be stated that on working days an average of 8 individual customers visit the garage daily.
Average service time is 4 hours. The workshop has 4 fully equipped and staffed
workstations that work shifts for 10 hours a day. This means that, on average,
32 hours are used out of the 40 working hours available in a day.
This
20% of the unused potential of the workshop could be filled with services for
fleet customers. Especially in the case of fleet customers who usually use
their vehicles quite intensively, most of the services will be periodic vehicle
maintenance. As a rule, activities related to periodic maintenance take less
time than vehicle repairs.
However,
signing contracts with fleet customers is associated with the need to ensure
appropriate high standards of services. In this case, the speed of reaction to
the breakdowns of fleet vehicles and short waiting times for periodic
inspections and technical services are particularly important.
Of
course, the company wants to retain its existing individual customers.
Therefore, services performed for fleet customers cannot significantly affect
the level of individual customer service. Therefore, it is difficult to
introduce absolute priority for fleet customers.
The
developed model of the workshop operation and the simulation tests performed on
it should answer the following questions:
1. What
is the actual level of untapped potential of the workshop?
Due to the random nature of individual customer vehicle applications and random
service times, the rough calculation of free capacity presented above does not
have to be true. In addition, there is a constant flow of time, which means
that the "lost potential" in a given day cannot be recovered due to a
randomly smaller number of reports. Therefore, it is necessary to carry out a
kind of "stress test" that will allow to determine the maximum number
of individual customers that can be served by the workshop.
2. What
is the maximum number of fleet customers that can be served? Assuming
that the number of individual clients is at the previously mentioned level. It
can be predicted that the results will largely depend on the selected analyzed
set of fleet vehicles and the accuracy with which their basic features will be
determined:
- vehicle make/model and the resulting maintenance
frequencies, as well as their time and scope;
- average daily mileage of vehicles and standard deviation of
mileage (assuming normal distribution truncated from left to zero).
3. What strategy to reserve time in
the work schedule of the workshop to choose? Two possible
strategies are considered. The first is to reserve time after the occurrence of
an incident involving the vehicle exceeding the mileage limit or the time limit
for scheduled maintenance. The second is to reserve time in advance based on
the vehicle's mileage forecast or the number of days remaining until the
service deadline is exceeded. The first strategy, assuming the equal treatment
of fleet and individual customers, will involve systematically exceeding the
limits. In the case of the latter, there is a high risk of prematurely
performing the service, which will probably not be appreciated by the fleet
customer.
3. SIMULATION SCENARIO
This paper adopted the following scenario of the
workshop operation described below, which has a direct impact on the structure
of the simulation model and the scope of empirical data that should be
collected before performing the simulation tests.
First, it is important to define the relationship
between the real time and the time step and simulation time. It was assumed that the work of a workshop would
be simulated during one calendar year. Additionally, it was assumed that a
fifteen-minute accuracy is sufficient to describe the duration of all essential
activities. Vehicle waiting times and service times will be measured with such
accuracy. Further, maintenance includes both periodic maintenance and repairs
resulting from the wear of parts or their failure. This means that 1 second of
simulation (time unit) will be equivalent to 15 minutes of real time.
The workshop is open on weekdays for 10 hours from
8.00 to 18.00 and on Saturdays for 6 hours from 8.00 to 14.00. To simplify the
simulation scenario, it was assumed that one real-time day is 40 steps of the
simulation time (working day). Non-working days are excluded and automatically
excluded from the simulation time. Due to this simplification, the vehicles
waiting in the service server modeling the workshop stands will not be
completed outside the workshop's working hours, and all unfinished vehicles on
a given day will naturally pass to the next day. This way, there is no need to
stop the server so that it does not count down outside workshop hours. Saturday
is a special day. In the simulation, it lasts the same as other working days
with the servers working 10 hours. On Saturdays, however, work is planned for
only 6 hours. This is true to some degree, as, on Saturdays, the workshop often
stays open longer to complete the rest of the week's repairs.
Tab. 1
Summary
of simulation times
|
Simulation Time |
Real Time |
|
1 |
15 minutes |
|
40 |
One working day of the
workshop (10 hours) |
|
|
One-year period,
excluding non-working days ( |
Orders
from individual clients appear at random intervals in the simulation time. It
was assumed that this is done following the exponential distribution with the average interval for individual vehicles,
which can be determined based on the workshop operation history. The estimated
time of service performance is also drawn for each order. In actual conditions,
this time is estimated based on an interview with the client and preliminary
examinations made by the shift manager. It was assumed that the forecast service time has a normal
distribution. The actual service time
may differ from the forecast and is the sum of the forecast and a random
disturbance also with a normal distribution. The service times cannot be
simultaneously shorter than the assumed minimum (for example, 2-time units).
The parameters of both normal distributions must be established based on the
historical data of the workshop operation.
During
the simulation, the fleet vehicles form a static set numbered consecutively
from one to the maximum number of fleet
vehicles. For each fleet vehicle, information should be collected on the
model, its total mileage in kilometers, average daily mileage and standard
deviation of the mileage. The daily mileage is assumed to follow the normal
distribution truncated from left to zero. Daily random mileage is rounded to
whole kilometers. During the simulation, the mileage and age of the vehicle
will be constantly modified every day.
However,
for each vehicle model, additional information on the periodic technical
inspections should be specified: after how many kilometers or days maintenance
should be performed and the estimated time of such inspection. In this case
also, the estimated time will be randomly different from the real time.
There
are three scheduled maintenance intervals for each vehicle model. The
maintenance activities of the higher range include activities of all the lower
ranges. Therefore, after performing the service of a given range, the mileage
counters in kilometers and days should be reset, together with the counters of
the lower ranges.
Fleet
vehicles can also experience breakdowns that the workshop should fix as soon as
possible. With intensive use of fleet vehicles, maintenance activities will
occur much more often than breakdowns. To simplify the model, it was assumed
that breakdowns of fleet vehicles are treated regardless of their technical
services. They represent a certain disruption of the process that occurs in the
system in time intervals subject to exponential decay with the average failure interval of the fleet
vehicles. In connection with the failure events, they will be numbered
consecutively and will not be related to the numbers of fleet vehicles.
Distinguishing between fleet vehicles, breakdowns and vehicles of individual customers
requires an additional parameter - status.
Each
order requires time reserved in the
workshop's work schedule. The schedule covers all the days in the calendar
year and all service stations in the workshop. Holidays and Saturday afternoons
are not available. Each service must be started and completed on one station.
During the booking process, the work schedule is searched from the day
following the day of reporting to find the first continuous and free period of
time greater than or equal to the forecasted service time. Services for
individual clients, the duration of which is longer than the assumed minimum,
may start at the end of one working day and end the next. Services for fleet
customers should start and finish in one working day (inspections usually take
less time than repairs). Failures do not require booking a place in the
workshop and go directly to the workshop.
To
simplify the model, it was assumed that customers do not resign from previously
agreed service dates and report to the garage promptly. In the future, the
model can be supplemented with this type of additional random disturbance.
Individual customers may cancel the reservation if the proposed free date is
too distant (for example, exceeds 2 weeks). This does not apply to fleet customers
referred for periodic inspections.
4. DESCRIPTION OF THE SIMULATION MODEL
The developed car workshop simulation model consists
of 7 subsystems (Figure 1): generating daily mileage of fleet vehicles,
generating orders for periodic maintenance of fleet vehicles, generating fleet
vehicle failures, generating orders for individual customers' vehicles, booking
places in the work schedule, modeling the operation workshop and a subsystem
for saving and displaying simulation results. The SimEvent
library of the Matlab/Simulink environment was used.
The possibilities of the Matlab Function block and
global variables were also intensively used to save information such as the
current simulation day, workshop work schedule, information on working and
non-working days, a table storing the mileage status of fleet vehicles, and a
table associating the vehicle model with its periodic technical services
(limits and service times).
The
simulation entity can be interpreted in two ways in the model. It depends on
where it occurs. At the beginning of its existence, the unit is an order for
the performance of a service. Based on the order, a place is reserved in the
workshop's work schedule. Then, the order awaits accepted orders on the server
and is transferred to the workshop at the right time, resulting from the
schedule. At this stage, the unit is already interpreted as a serviceable
vehicle.
Each
entity (order/vehicle) has a set of attributes that are used at different
stages of the simulation. These are:
Status
– 1 means a fleet vehicle in periodic maintenance, 2 - a fleet vehicle
sent to the workshop due to a breakdown, 3 - a vehicle of an individual
customer.
IdVeh
–the number (from the pool of numbers) of the fleet vehicle intended for
periodic maintenance or the sequence number of the generated individual
customer vehicle or failure of the fleet vehicle.
Priority –
priority used in the queue of vehicles waiting for the workshop. Fleet vehicles
going to the workshop in an emergency have priority 2, others 1.
AverServTime –
estimated time of the service. Randomly generated for individual customers' vehicles
and fleet vehicle failures. In the case of fleet vehicles, it results from the
type of periodic maintenance and is deterministic.
RealServTime –actual
time of service in the workshop. It is a randomly disrupted forecast time.
Stand –
the number of the service station in the workshop to which the vehicle is being
driven.
TimeShift – allows
specifying the first day from which the schedule will be searched for a free
time. This way the service can be postponed.
WaitToServ – time
spent in the server of accepted orders.
Path –auxiliary
attribute, allows control of the entity movement in the simulation.

Fig. 1. A model
simulating the work of the workshop and the daily mileage of vehicles
The
subsystem of daily mileage generation for fleet vehicles modifies the vehicle table every working day by
increasing the mileage counters in kilometers (randomly) and days. Non-working
days, which are normally not included in the simulation, are also included in
the mileage measured in days based on the working days’ table. The
subsystem also resets vehicle mileage counters after completion of maintenance.
Modification of the vehicle table always takes place in 1 simulation time unit
(15 minutes real time) before the end of the working day. This is to prevent
simultaneous access to the table by the subsystem generating service requests
based on it.
The
current state of the vehicle table is saved in a journal and can be
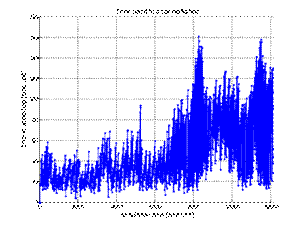
additionally analyzed later. An exemplary history of a selected fleet vehicle,
the mileage of which was subject to the distribution N (469.68), is shown in
Figure 2. During the calendar year (all days of the year were considered), the
vehicle underwent consecutive inspections of 2,1,3,1,2,1,3 after covering 20,40
and 80,000 km, respectively. The timeline also shows the date of submission of
the inspection request (asterisk) and the date of its actual completion
(circle). Exceeding the mileage limits amounted to 1612, 970, 2382, 1543, 1829,
1990, and 2197.
An
additional task of the subsystem is the modification of the global variable
indicating the current day of the year, which is performed at the end of each
working day. The current day of the year is used by the vacancy reservation
subsystem.
The vehicle table contains the following fields:
vehicle number, total mileage, age, average daily mileage, standard deviation
from the daily mileage; and three sets of fields: inspection ID, odometer, and
day counter; for each of the three maintenance areas. The last field is used to
save the type of inspection and allows to distinguish the inspection resulting
from exceeding the limit of kilometers or days. By changing the sign of the
value in this field, the end of the service by the workshop is also signaled,
which is the basis for resetting the counters. The inspection identification
fields refer to an additional periodic maintenance table, which contains the
following information: service limit in kilometers, limit in days, forecast
duration of the inspection (deterministic), and variance of the random time
disturbance (distribution ![]()
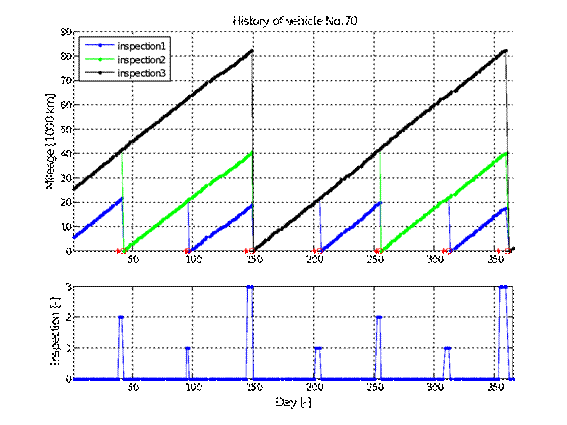
Fig. 2. An exemplary history of technical inspections of a selected
fleet vehicle
In
the fleet vehicle maintenance order generation subsystem, at the beginning of
the simulation and the beginning of each working day, a unit stream
corresponding to the full set of fleet vehicles is simultaneously generated.
Based on the vehicle numbers and entries in the vehicle table and the
inspection board, vehicles/orders sent to the workshop are selected. The
remaining units are turned off. The "order exit" event is saved to
the reservation system. Two strategies for selecting vehicles were implemented
as described in paragraph 2. In the case of the first strategy, the delay in
booking a place in the workshop work schedule is a random number of days with a
Poisson distribution with a given average equal to, for example, 1 day. This
simulates the phenomenon of postponing the declaration of a fleet vehicle due
to its involvement in early ordered transports. In the case of the second
booking strategy, it is delayed by a fixed number of days; however, the booking
decision is made well in advance.
The
structure of the subsystems generating breakdowns of fleet vehicles and the
orders of individual customers is very similar. Orders are generated based on
the given average failure interval
and the average reporting interval of
an individual customer and are subject to an exponential distribution. Each
order is assigned a predicted random service execution time and the real time
resulting from a random forecast disruption. The real time of service
performance will be needed only in the subsystem imitating a workshop. However,
in the model, it does not matter at what stage this value is drawn. Each order
generation event is recorded.
All
orders of individual and fleet customers, as well as breakdowns, are sent to
the reservation subsystem. The subsystem searches for a place in the workshop
work schedule that is adequate to the forecasted time for the service and
assigns a service station. Calculates the time when the vehicle should reach
the workshop and stores the order in the order server until then. The unit leaving
the reservation subsystem can further be interpreted as a vehicle headed for
the workshop. Failures are prioritized, the least loaded workstation is
searched for, and the vehicle with the breakdown is immediately directed to it.
Optionally, the priority can be turned off, then failures will be treated in
the same way as other orders.
Ultimately,
all units/vehicles generated in the simulation go to the workshop, where they
are allocated to stands. The time interval from the unit's arrival at the
workshop to the time the unit is put out of service after the service is
performed is measured. All service performance events are saved to a separate
file. Information about the end of service for fleet customers is provided via
the vehicle table.
It
is assumed that normally vehicles arrive at the site exactly at the time
planned in the schedule. Using the parameter earlier arrival, it is possible to force the appearance of the
vehicle ahead of time (but not earlier than the beginning of the next working
day). In this way, the free time of the service stations in the event can be
used because the actual service time was shorter than planned. On the other
hand, arriving earlier increases the total time the vehicle spends in the
workshop.
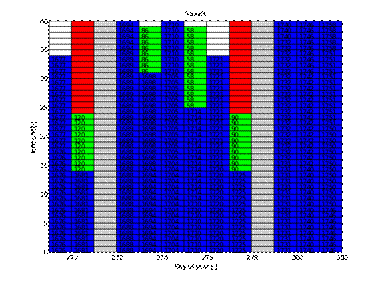
Fig. 3. A fragment of the workshop work schedule completed during the
simulation
It
is also possible to artificially thicken orders in the schedule using the overbooking parameter. In the model,
this parameter can be used to shorten the forecasted service time, which,
however, cannot be shorter than the assumed minimum
reservation time. However, the use of overbooking is risky and will almost
certainly cause at least temporary blockages and prolongation of the vehicle's
stay in the workshop.
Naturally, at the end of the year, the workshop's work
schedule is already full, and some of the vehicles must be diverted to the next
year. The work schedule is available after the simulation is completed as a
disk file, and on its basis, additional analyzes of the annual operation of the
workshop can be made. Figure 3 shows an exemplary excerpt from the schedule,
days 270 to 282, workshop stand number 3. Blue is for individual customer
reservations; green is for fleet customers and white is unused space.
Additionally, gray means non-working days and red means afternoon hours on
Saturdays.
5. ASSESSMENT OF THE WORKSHOP POTENTIAL WITH
SIMULATION METHODS
The
simulation research started with the assessment of the workshop's
potential. Only applications from individual customers were considered. A case
was analyzed when the average interval between consecutive requests was 5-time
units (approximately 8 clients per day). The customers arrived at the workshop
exactly on time. There was no overbooking when booking seats. The projected
service time was described with the N
(16.2) distribution, while the real time was the sum of the forecast time and
the disturbance with the N (0.4)
distribution. At the same time, none of those times could be smaller than 2
units.
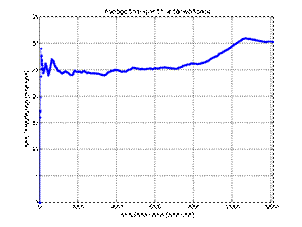
When
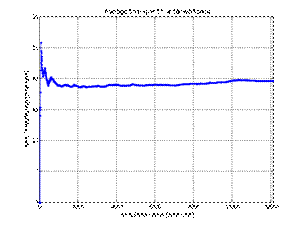
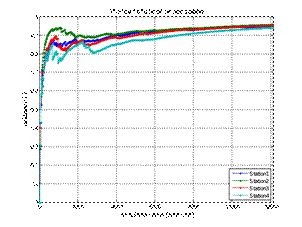
analyzing Figure 4, it can be noticed that the most time spent in the workshop
by individual customers' vehicles was within one working day. Only a few
vehicles spent more time in the workshop, but not longer than 1.5 working days.
Disregarding the "switch-on effect" at the start of the simulation,
the average time spent in the workshop was stable at around 20 units (half a
working day). The waiting time for the service was usually 3 working days. The
degree of use of the individual workshop stands was between 70 and 80%. The
uneven load of the positions results from the algorithm used for searching for
vacancies - the established order of positions when viewing the workshop work
schedule. During the 303 working day simulation, 2,322 repair orders were
generated from individual customers. Subsequently, 2,314 vehicles were
serviced, 7 vehicles were registered for another year, while the service of one
vehicle was extended for another year.
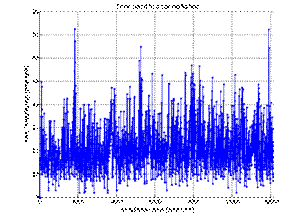
After
the simulation was completed, the workshop work schedule was analyzed and it
was found that the following positions were not used at individual positions:
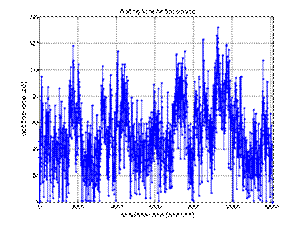
13.3, 11.3, 17.3, and 24.3% of the available time. The histogram of Figure 5
shows that the largest amount of free time periods is between 5 and 8 units.
There are also sections with a length of 40 units (working day), and this
applies mainly to stand number 4. Eventually, based on the results of the first
simulation, it can be concluded that the level of customer service is high,
while the degree of use of the stands is a bit too low.
The
estimated time of the service plays an important role in the process of booking
a visit to the workshop. In actual working conditions of the workshop, this
time is assessed by the workshop manager based on an interview with the
customer and a preliminary inspection of the vehicle. The accuracy of the
forecast depends on the experience of the workshop manager. There is a tendency
to systematically lower the service time. This phenomenon increases the
occupancy of positions and the time spent in the workshop but does not affect
the waiting time for the service itself (entries in the schedule). During the
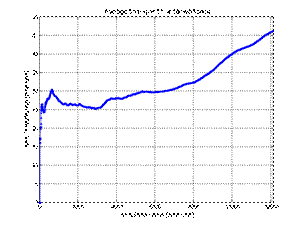
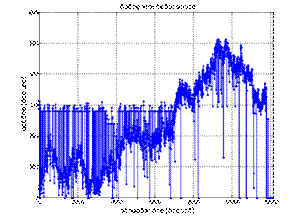
second simulation, the service time disturbance distribution was changed to a
very pessimistic N (2,4), leaving the remaining
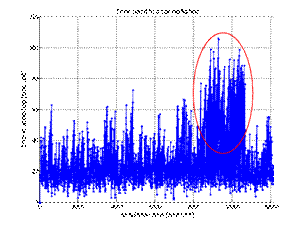
parameters unchanged. The time spent in the workshop has significantly
increased, and a minor blockage can be observed at the end of the year (Figure
6). The occupancy of positions increased by approximately 10%.
|
|
|
|
|
|
Fig. 4. Summary of the results of the first simulation (applications
with interval 5)

Fig. 5. Histogram of all free time slots in the work schedule
|
|
|
Fig. 6. Increase in service time due to the systematic decline in the
forecast
|
|
|
|
|
|
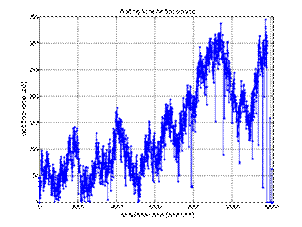
Fig. 7. Summary of the results of the third simulation (applications
with interval 4.5)
The
third simulation was carried out under the same conditions as the second one,
however, shortening the interval between successive applications to 4.5 units.
A total of 2,635 orders were generated, of which the workshop handled 2,534; 88
vehicles were registered for the next year, and the repair of 13 vehicles was
extended for another year. Based on the analysis of the results (Figure 7), it
can be concluded that with such a number of orders, the workshop has already
reached its limit. The time spent in the workshop systematically increases over
one working day. At the end of the year, there is a need to wait a long time
for the service itself - about 8 days. The use of the positions reaches 95%.
Further
shortening the reporting interval to 4 units generates 2,957 orders. However,
the workshop serviced only 2,607 vehicles, which is a little more than what was
achieved in the third simulation. On the other hand, as many as 257 customers
resigned from subscribing because the waiting time for the service exceeded 14
days.
Summarizing
the results of all simulations, it can be assessed that the workshop can handle
orders appearing with an interval of 5-time units at a good level. The
simulation shows that it will be slightly less than 8 clients a day. Therefore,
it is the number that results from the observation of the history of the
workshop to date. At the same time, at least a dozen or so percent of free time
is left. These are often periods of time in the order of 2-3 hours that can be
used for periodic fleet vehicle inspections.
The
simulations also showed that even if the systematic error in forecasting the
service time was extended by an average of plus 2 units (half an hour), the
workshop was still operating efficiently enough. The available historical data
on the work of the workshop does not allow assessing what exactly this error
was.
6. RESEARCH ON THE IMPACT OF FLEET VEHICLES
Based
on the parameters of the first simulation discussed in the previous paragraph,
an additional stream of fleet vehicles was included in the model (periodic
maintenance and breakdowns). The impact on the workshop operation of an
additional 150 fleet vehicles is presented below.
To
obtain the most reliable simulation results, it would be necessary to know the
exact parameters of the entire vehicle population, including the average daily
mileage. The owners of the fleet have this data. Due to the difficulties in
obtaining data before signing the relevant contracts, a randomly generated
virtual population of vehicles was used in the simulation. Seven classes of
fleet vehicles with a load capacity of up to 3.5 t were selected, which meant
21 different scopes of technical inspection. The average daily mileage of the
generated fleet was uniformly distributed from 50 to 500 km. It was assumed
that the standard deviation of the daily mileage accounted for 10% of the
average mileage. The failures were treated as events independent of technical
inspections, occurring with an interval of 800-time units.
The
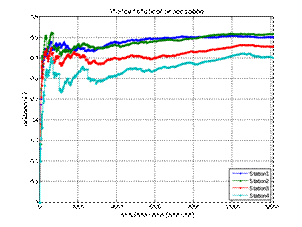
simulation results are summarized in Figure 8. In total, 432 orders for the
inspection of fleet vehicles and 17 failures were generated. The workshop
serviced 2,717 vehicles during the year. Fifty-four orders were saved for the
next year. The records of the fleet vehicles in the work schedule were carried
out following the first strategy, that is, after the fleet vehicle exceeded a
certain mileage or time limit. Observably, additional orders do not significantly
affect the time spent by vehicles in the workshop. However, at the end of the
year, there is a clear increase in waiting time for the service, which is even
up to 10 days.
The
second strategy for stocks of fleet vehicles was also tested, based on the
forecasted mileage of 7 days in advance. In this case, the average service time
did not change, but the waiting time for it increased. There was an unfavorable
phenomenon - 28 individual customers resigned from subscriptions due to
excessively long waiting times (Figure 9).
Figures
10 and 11 compare the exceedance of the mileage limit in the case of making
entries to the workshop according to two strategies. It can be seen that in the
case of earlier records, the maximum exceedances are almost halved, but it is
also possible to perform an inspection prematurely. The calculated average for
all vehicles with average individual exceedances is 1194 and 370 km,
respectively, depending on the strategy. The number of 150 fleet vehicles is the limit value at which the workshop
functions properly and does not discourage individual customers by waiting too
long for the service. The first strategy for scheduling entries is more
advantageous because on average, inspections take less time than repairs, and
it is easier to fill the empty spaces with them. Of course, one has to consider
that the limits of inspection kilometers will be exceeded, but as calculated,
they are not too large. The second strategy causes blocking of the terms at the
beginning of the working day, which makes it impossible to find a free period
of time on the border of two days in the case of individual customers.
|
|
|
|
|
|
Fig. 8. Comparison of simulation results with an additional stream of
fleet vehicles
|
|
|
Fig. 9. Average time spent in the workshop and waiting time for the
service
(Second strategy for fleet vehicle records)
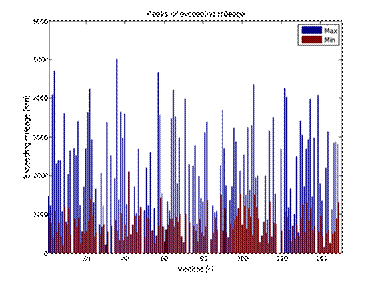
Fig. 10. Strategy 1 - maximum and minimum exceedances of the mileage
limit
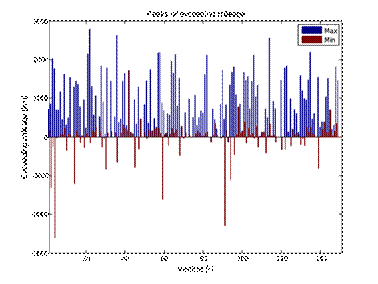
Fig. 11. Strategy 2 - maximum and minimum exceedances of the mileage
limit
7. CONCLUSIONS
The
simulation model of a workshop that simultaneously serves a stream of
individual and fleet customers was used to detect possible blockages and
establish safe boundary parameters. However, this model is quite universal.
Assuming the required parameters, an inverse analysis is possible to estimate
the number of necessary positions in the workshop. Additional statistical
analyzes can also be performed after performing the simulation based on files
documenting the events and the completed work schedule. Although the model was
created based on the analysis of a specific case, it is easy to modify and
adjust to other conditions and needs.
The
problem of inspecting fleet vehicles does not only concern transport related to
the supply chain. The increase in the number of vehicle rental companies and
the developing idea of vehicle sharing may increase the demand for this type of
service in the future. The reason for the inspection may be not only exceeding
the mileage limit and performing maintenance following the manufacturer's
recommendations. Moreover, it is equally important to systematically monitor
the technical condition of rented cars and react quickly to various types of
minor damage or devastation.
Based
on the simulation analysis of the operation of the selected workshop, it was
possible to determine that the workshop will work properly when individual
customers report with an interval of not less than 4/5 hours. On the other
hand, the limit number of fleet vehicles serviced by the garage is 150. The
most advantageous from the viewpoint of the garage's interests is enrolling
fleet customers, after the necessity to perform an inspection, in the first
free place in the schedule. In this case, however, it should be considered that
some of these inspections would be carried out more than the mileage limit.
This can be problematic in newer vehicles, in which the onboard computer limits
the power or even stops the vehicle if it is not serviced on time. The results
are critically influenced by obtaining reliable and detailed data on fleet
vehicle mileage.
References
1.
Aliyu Aliyu Isah, Tukur
Abdulkadir Sulaiman, Abdullahi Yusuf. 2015. “Modeling and
simulation analysis of health care appointment system using ARENA”. International Journal 4(1): 1-7.
2.
Block Christian, Dominik Lins, Bernd Kuhlenkötter. 2018. “Approach
for a simulation-based and event-driven production planning and control in decentralized
manufacturing execution systems”. Procedia CIRP 72: 1351-1356.
3.
Buchmann Alejandro,
et al. 2010. “Event-Driven services: Integrating production, logistics
and transportation”. In: International Conference on Service-Oriented
Computing. Springer, Berlin, Heidelberg. P. 237-241.
4.
Choi Byoung
Kyu, Donghun Kang. 2013. Modeling and
simulation of discrete event systems. John Wiley
& Sons.
5.
Czech Piotr. 2011. „An intelligent approach to
wear of piston-cylinder assembly diagnosis based on entropy of wavelet packet
and probabilistic neural networks”. Communications
in Computer and Information Science 239: 102-109. DOI: https://doi.org/10.1007/978-3-642-24660-9_12.
Springer, Berlin, Heidelberg. ISBN: 978-3-642-24659-3. ISSN: 1865-0929. In:
Mikulski Jerzy (eds), Modern transport telematics, 11th
International Conference on Transport Systems Telematics, Katowice Ustron, Poland, October 19-22, 2011.
6.
Czech Piotr. 2013. „Diagnose car engine exhaust
system damage using bispectral analysis and radial
basic function”. Advances in
Intelligent Systems Research 30: 312-315. DOI:
https://doi.org/10.2991/iccnce.2013.78. Atlantis Press. ISBN:
978-90-78677-67-3. ISSN: 1951-6851. In: Zheng D., Shi J., Zhang L. (eds), Proceedings of
the International Conference on Computer, Networks and Communication
Engineering (ICCNCE), Beijing, China, May 23-24,
2013.
7.
Figlus T. 2019. “A method for diagnosing gearboxes of means of transport using multi-stage filtering and entropy”. Entropy 21(5): 1-13.
8.
Figlus T., J. Gnap, T. Skrúcaný, B. Šarkan,
J. Stoklosa. 2016. „The use
of denoising and analysis
of the acoustic signal entropy in diagnosing engine valve clearance”.
Entropy
18(7): 1-11.
9.
Fornasiero Rosanna, Andrea Zangiacomi, Marzio Sorlini. 2012. „A cost
evaluation approach for trucks maintenance planning”. Production Planning & Control
23(2-3): 171-182.
10. García
Juan Martín. 2020. Theory and practical exercises of system dynamics:
modeling and simulation with Vensim PLE. Preface John Sterman. System
Dynamic Group. MIT Sloan
School Management.
11. Goyal
Suresh K., A. Gunasekaran. 1992. “Determining
economic maintenance frequency of a transport fleet”. International
Journal of Systems Science 23(4): 655-659.
12. Jalel Ben
Othman, et al. 2021. “Queuing theory based simulation model for vehicular
mobility”. In: ICC
2021-IEEE International Conference on Communications.
IEEE.
P. 1-6.
13. Jilcha Kassu, Esheitie Berhan, Hannan Sherif. 2015.
“Workers and Machine Performance Modeling in Manufacturing System Using
Arena Simulation”. Journal of Computer Science & Systems Biology 8(4):
185.
14.
Kozłowski E., K. Antosz, D.
Mazurkiewicz, J. Sęp, T. Żabiński. 2021. „Integrating advanced
measurement and signal processing for reliability decision-making”. Eksploatacja i Niezawodnosc – Maintenance
and Reliability
23(4): 777-787.
15. Małopolski Waldemar,
et al. 2012. “Modeling and optimization of manufacturing systems using
Arena software”. Czasopismo Techniczne. Mechanika 8-M(22): 91-108.
16. Marseguerra Marzio, Enrico Zio. 2000. “Optimizing maintenance and
repair policies via a combination of genetic algorithms and Monte Carlo
simulation”. Reliability Engineering & System Safety 68(1): 69-83.
17.
Michalski R., S. Wierzbicki.
2008. „An
analysis of degradation of vehicles in operation”. Eksploatacja i Niezawodnosc – Maintenance
and Reliability
1: 30-32.
18.
Mickūnaitis V., S. Nagurnas. 2002.
„The improvement of the technical
exploitation of automobiles”.
Transport 17(4): 143-146. DOI: ttps://doi.org/10.3846/16483840.2002.10414031.
19. Raposo
Hugo, et al. 2021. “An Integrated Model for Dimensioning the Reserve
Fleet based on the Maintenance Policy”. WSEAS
transactions on systems and control 16:
43-65.
20. Rudyk Tomasz, Emilian Szczepański,
Marianna Jacyna. 2019. „Safety factor in the sustainable
fleet management model”. Archives of Transport 49: 103-114.
21. Shamsuddoha Mohammad, Alexandru Mircea Nedelea. 2013. “A Vensim
based analysis for supply chain model”. Ecoforum
Journal 2(2): 8.
22. Valigura K.,
M. Foltin, M. Blaho. 2009. “Transport
system realization in simevents tool”. Technical
Computing Prague.
23. Wainer Gabriel A., Pieter
J. Mosterman (ed.). 2018. Discrete-event modeling and simulation: theory and
applications. CRC press,
24. Wang
Yali, et al. 2019. “Vehicle fleet maintenance
scheduling optimization by multi-objective evolutionary algorithms”. In: 2019 IEEE
congress on evolutionary computation (cec). IEEE. P. 442-449.
25. Zhang
Yue, et al. 2017. “A simevents model for hybrid
traffic simulation”. In: 2017
Winter Simulation Conference (WSC).
IEEE. P. 1455-1466.
Received 03.02.2022; accepted in
revised form 09.04.2022
![]()
Scientific Journal of Silesian University of Technology. Series
Transport is licensed under a Creative Commons Attribution 4.0
International License