Article
citation information:
Vakulenko, I.A.,
Plitchenko, S., Kurt, B., Askerov,
H., Proydak, S., Erdogdu, A.E. Influence of plastic deformation carbon steel on the process of
burning electric arc. Scientific Journal
of Silesian University of Technology. Series Transport. 2021, 112, 211-218. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2021.112.7.17
Igor Alex VAKULENKO[1], Sergey PLITCHENKO[2], Bulent KURT[3], Hangardas ASKEROV[4], Svetlana PROYDAK[5], Ahmet Emrah ERDOGDU[6]
INFLUENCE OF PLASTIC
DEFORMATION CARBON STEEL ON THE PROCESS OF BURNING ELECTRIC ARC
Summary. During a study of the
combustion process of a direct polarity electric arc, a directly proportional
dependence of the electric current value on the degree of cold plastic
deformation of carbon steel used as an electrode was found. To calculate the
value of the electric current during arc burning, in the indicated ratio, it
was proposed to replace the surface tension force of the liquid metal with the
surface tension of ferrite of plastically deformed carbon steel. Calculation of
the ferrite’s surface tension value on the deformation degree of the
steel under study through the size of the coherent scattering regions was used
to explain the observed dependence of the electric current during arc burning.
From the analysis of the considered correlation ratios, it was found that with
an increase in the cold deformation degree, the refinement of the coherent
scattering regions results in the ferrite’s surface tension increase and
consequently, to an increase in the electric current during arc burning. Comparative
analysis of the obtained results of calculating the value of electric current
during arc burning through the surface tension of ferrite of cold-deformed
carbon steel showed a fairly good coincidence with experimental data. The
differences did not exceed 9%.
Keywords: substructure, density dislocation, electric
current, plastic deformation, cementite, ferrite
1. INTRODUCTION
When repairing
railway transport elements that are subject to significant wear during
operation, electric arc surfacing technologies are commonly used [1]. The technologies for the repair of
worn-out parts provide not only the restoration of the shape but the
achievement properties in the deposited volume of metal, close to the original
state. One of the main conditions in achieving high-quality restoration of
products is the use of electrodes for surfacing with a chemical composition
close to the base metal. Compared to the electrodes for electric arc welding,
the repair technology of worn-out surfaces by weld deposition does not provide
for restrictions on the carbon and alloying elements concentration for the
electrode wire. In general, rather difficult conditions for stabilisation of
arc combustion [2-4] can be reduced to two main processes: changing the state
of metal aggregation and transferring it to the weld pool [5-9]. When the first
portions of liquid metal appear, a static pressure gradient directed towards
the electrode axis, which is caused by the pinch effect, arises at the end of
the electrode. As the electric current increases, a change in the ratio between
the pinch effect and surface tension force of liquid metal takes place. The
moment of achieving equality between the said effects corresponds to the stage
of completion of the liquid metal’s drop formation capable of being
transferred to the deposition surface. The electric current value corresponding
to the fulfilment specified condition is considered a critical value. The
critical value of the electric current is estimated by parabolic dependence on
the electrode diameter and surface tension force of the liquid metal.
Furthermore, the correct choice of the electric current value during arc
burning, in comparison with the critical value, is one of the main factors in
the formation of a high-quality layer deposited metal. On this basis, the force
of surface tension metal and strength of the electric field in comparison with
other factors should prevail when choosing conditions for the combustion of an
electric arc [7]. The known dependence surface tension force on the characteristics
of crystal structure metal can be considered as evidence of the possible
influence of structure parameters on the specified characteristic. Based on
this, the choice main structure element of the electrode metal can be used to
explain the nature of the change at the magnitude of the electric current
during arc burning. For cold-worked metal, such characteristic can be
substructure parameters
2. MATERIALS AND METHODS
To
study the process of electric arc burning, a cold-drawn wire 1 mm in diameter
made of steel with 0.8% C, 0.84% Mn, 0.51% Si, 0.02% S, 0.014% P was used as an electrode. To achieve various degrees of cold
plastic deformation, the diameter of the workpiece was selected in such a way
that, after drawing to diameter 1 mm, the required reduction was obtained. To achieve
various degrees of cold plastic deformation and a constant final wire diameter,
the blanket diameter was selected in such a way as to obtain the required
reduction value after drawing to a diameter of 1 mm. For a uniform arrangement
of cementite particles and exclusion of its participation in the plastic
deformation, steel blanks were martensite quenched
and tempered at a temperature of 650°C for 1 hour
(Figure 1a). The workpieces were heated to prevent
oxidation in ampoules with the preliminary evacuation of air. Cold drawing of
workpieces was carried out on a wire mill at deformation values (ε) of 17,
30, 50, 60, 70 and 80%. The substructure was investigated under the light and
electron microscope UEMV-100K at an accelerating
voltage of 100 kV. The substructure elements size of the cold-drawn steel was
determined by quantitative metallographic methods. The size of coherent
scattering regions was estimated by dislocations density using X-ray structural
analysis by reflection methods (110) [10]. Investigations of process combustion
of electric welding arc were carried out on a special stand (Figure 2).
The source of direct electric current for the straight polarity arc was a
PSG-500 welding converter. The wire (3) is fixed vertically (2) at a special
table as an electrode. On the table (1), there is a removable plate (4) made of
low carbon steel. To form an electric arc and stabilise the process of its
combustion, the gap between the end of electrode (3) and the plate (4) (no more
than 1-1.5 mm) is filled with a powder mixture (6) from the components of
electrode coating for manual arc welding. After the electric current is applied
to the terminals (7), the electric arc is ignited by introducing a graphite rod
(5) into the gap between electrode and plate (4). During the period of arc
burning, value of the electric current is determined under conditions of its
stable burning.
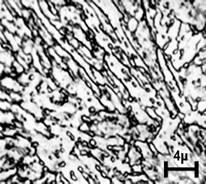
a
b
с
Fig.1. Steel
structure after quenching and tempering at 650°C
(a) and
follow plastic deformation 17% (b,c)
3. RESULTS AND DISCUSSION
Electric arc formation is largely determined by the
transition processes of metallic material into a liquid state. In this case,
change in surface tension force determines conditions for the liquid phase
formation, the shape and dispersion of drops [4]. Moreover, increase in
electric current value, through the liquid metal’s temperature increase
is accompanied by a decrease in surface tension and the dispersion of drops
associated with it.
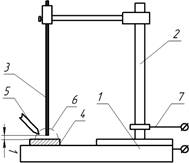
Fig.
2. The schema representation stand for study combustion process of the electric
arc
From the ratio of the
hydrostatic pressure at pinch effect and the value of metal surface tension, a
dependence for estimating the critical value of the electric current (Ic) when the drop is detached
from the electrode is proposed [7]:
,
(1)
where sL – surface tension of
the liquid metal, de
– electrode diameter, A –
constant value. For a wide variety of steels, A is 32.7 A/dyne0,5 [6]. Evaluation Ic
according to (1) for low carbon steel at sL = 1220 dyne/cm, A = 32.7 A/dyne0,5 and de = 1 mm, showed a value about 1140 A, although the
value from experiment was 480 A.
Similar differences between
calculated and experimental values were obtained for steel with 0.12% C, 18% Cr, 9% Ni, 1% Ti (190 A) [7],
and the steel with 0.06% C of the
same alloying, additionally 40% less than the calculated ones. The results
obtained indicate insufficient accuracy of the Ic estimate by the ratio (1). On the
other hand, during the deposit welding of the metal, the value of electric
current under conditions of stable arc burning is a more important
technological characteristic in comparison with Ic.
In addition to this, the observed differences between experimental and
calculated values Ic according to (1) indicate the need to
search for other characteristics that will make it possible to predict the
electric current value during deposit welding. The analysis of the experimental
data [2, 4, 8, 9] shows that the electric current value under conditions of
stable arc burning (I) is
approximately an order magnitude less than those calculated according to (1).
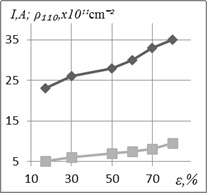
Furthermore, observed similar nature of change in I and density of accumulated dislocations (r) from ε (Figure 3a) indicate possible use
of substructure parameters of cold-deformed steel to describe I. To explain the given ratios,
dependence of metal surface tension on dislocation density was used [11].
Considering that the volume fraction of cementite in the steel under study is
about 12%, the particles are uniformly distributed in the ferrite matrix, and
ferrite is a structurally continuous phase, an attempt was made to replace sL in (1) by the surface tension of carbon steel
ferrite (sf). Consequently, the main
effect on ferrite surface tension at solid state should be exerted by its
structural state. Calculation sf was carried out according to
the ratio [11]:
,
(2)
where G – is the shear modulus of ferrite (0.82
), b – is the Burgers vector
(2.3
cm), l – is the distance between
dislocations, cm. The relation (2)
was obtained for ferrite of low carbon steel after small plastic
deformations, with an almost uniform distribution of dislocations. However,
already after 7-10% of plastic deformation, the decomposition of uniform
distribution of dislocations into the periodic structures begins [12] (Figure 1b), and after 20-30% dislocation cells are being formed
(Figure 1c).
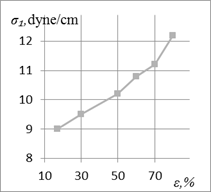
a
b
c
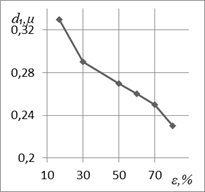
Fig. 3. Influence degree of reduction during drawing (ε) steel with 0.8% C after
improvement on the density of dislocations at reflection (110) (■) and
magnitude electric current of the arc by straight polarity (♦) –
(a); d
(b) and s1 (c)
The size of dislocation cells in
cold-deformed high-carbon steel is limited by the distance between cementite
particles. To estimate the distance between particles (l) for the steel under study, the relation is used
[13]:
,
(3)
where D – is the diameter of particles, f – their volume fraction.
For the particles with average
diameter of 0.32μ, l in steel was about 0.6 μ. After beginning of
dislocation cells formation, increase in total dislocations density in metal is
accompanied by their redistribution into those located inside the cells and
presented in the form of sub-boundaries. Based on such recombination of
dislocations, the size of dislocation cells should be only a certain fraction of l, which will decrease in proportion to ε. In this case, the width of
individual sub-boundaries can reach up to half the diameter of the dislocation
cell itself (Figure 1c), which significantly
complicates the assessment of its effective size. Based on this, estimation of
the dislocation cell size according to the results of electron microscopy for
calculating I will inevitably lead to
significant errors. As an alternative to estimating the dislocation cell size
by electron microscopic studies, to calculate the surface tension of the steel
under study (s1), ratio (2) with the replacement of l by the size of coherent scattering
regions (d1)
should be used. The value of d1 was calculated using the dependence:
,
(4)
where 
– the dislocation density (Figure 3a). In turn, was determined by the ratio [10]:
,
(5)
where m =
0.8, b – the broadening of X-ray
interference (rad) at reflection (110) – (r110),
q – is the interference angle, b – is the Burgers vector.
The given nature of change d1
from ε (Figure 3b)
corresponds to the accumulated dislocation density during steel drawing (Figure
3a) and qualitatively coincides with the results of
evaluating the dislocation cellular structure of similar steels. As a result of
replacing l by d1 in (2), the calculated
values of s1 are
shown in Figure 3c. The monotonous nature of increase
in s1 with increasing ε fully justifies the expected change of I. After replacing sL by s1 in (1),
the calculation of electric current during arc burning (I1)
from ε, at A = 32.7 A/dyne0,5 was carried out according to the
ratio:
(6)
Comparative analysis of I1 with I (Figures 3a and 4a) testifies only to
qualitative coincidence according to the dependences. The differences by
absolute values between I and I1 are
approximately 10-20%, which may be due to the lack of accounting influence
volume fraction of cementite on I1.
Indeed, the use of a carbon equivalent during the development of most welding
technologies indicates the need to consider carbon concentration in steel when
calculating I. According to [13], dependence (3) is
obtained from the ratio λ~(1-f)N‾¹, where N – is the total
number of particles per unit length of the random secant. Based on this, it was
proposed to change ratio (6) to the form:
(7)
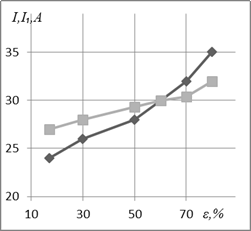
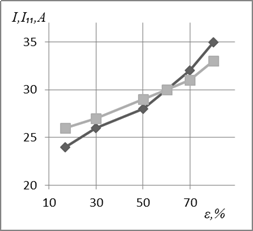
а
b
Fig. 4. Influence
of ε on I (♦) and
calculation (I1),
according to (6) (■) – (a) and (I11), according to (6а) (■) – (b)
The
calculation results I11 according to (7) are shown
in Figure 4b. Comparative analysis of absolute values
of electric current showed a decrease difference between I11 according to (7)
and I to
8-9%. Thus, additional consideration of cementite volume fraction in steel made
it possible to increase the estimation accuracy of the electric current during
deposit welding using a cold-drawn high-carbon steel wire as an electrode.
5. CONCLUSIONS
1. The electric current value during
the arc burning of straight polarity for carbon steel electrode is a
proportional degree of cold plastic deformation.
2. To estimate the value of electric
current during arc burning, the dependence of ferrite surface tension from
substructure parameters cold-deformed steel was used.
3. The size of coherent scattering
regions was chosen as a main substructural element of
cold-worked steel for calculating the surface tension of ferrite.
4. Estimation of the value of electric
current during arc burning based on the dependence from the size of coherent
scattering regions and volume fraction of cementite in cold-drawn carbon steel,
showed a satisfactory coincidence with the experimental data.
References
1.
Ostash O.P., V.H. Anofriev, I.M. Andreiko, et.al..2013. “On the
concept of selection of steels for high-strength railroad wheels”. Materials Science 48: 697-703. DOI: 10.1007/s11003-013-9557-7.
2.
Murphy A.B. 2015. “A perspective on arc welding research:
the importance of the arc, unresolved questions and future directions”. Plasma Chemistry and Plasma Processing 35: 471-489. DOI: 10.1007/s11090-015-9620-2.
3.
Ravichandran M., N. Sabarirajan, T. Sathish, et.al. 2016. “Effect of welding parameters on
mechanical properties of plasma transferred arc welded SS 202 plates”. Applied Mechanics & Materials 852:
324-330. DOI: 10.4028/www.scientific.net/AMM.852.324.
4.
Ogino Y., Y. Hirata.
2015. “Numerical Simulation of Metal Transfer in Argon Gas-Shielded GMAW”. Welding
in the World 59: 465-473.
DOI: 10.1007/s40194-015-0221-8M.
5.
Ke L., W. Zhisheng, Z. Yanjun, et.al. 2017. “Metal transfer in submerged arc
welding”. Journal of Materials
Processing Technology 244: 314-319. DOI: 10.1016/j.jmatprotec.2017.02.004.
6.
Tanaka M., K. Yamamoto, S. Tashiro.
2008. “Metal vapour behaviour
in gas tungsten arc thermal plasma during welding”. Welding in the World 52: 82-88. DOI: 10.1007/bf03266686.
7.
Petrov A.A. 1978. “Shielded gas welding. Welding
in mechanical engineering”. Engineering,
Moskow 1:
504.
8.
Shi L., Y. Song, T. Xiao, et. al. 2012. “Physical characteristics of welding
arc ignition process”. Chinese J.
of Mechanical Engineering 25: 786-791.
9.
Zhang
P., G. Li, H. Yan, et.al. 2020. ”Effect
of positive / negative electrode ratio on cold metal transfer welding of 6061
aluminum alloy”. The International
J. of Advanced Manufacturing Technology 106: 1453-1464.
10. Guinier A. 1956. Theorie et Technique de la ragiocristallographie.
Dunod, Paris. [In French: Theory and Technique of ragiocrystallography].
11. Baranov A.A. 1969. „About the initial stages of spheroidization cementite in steel”. Proceedings of the USSR Academy of
Sciences, Metals 3: 104-107.
(In Rusian).
12. Holt D.L. 1970.
“Dislocation cell formation in metals”. J.Appl.Phys. 41: 3197-3202.
13. Liu C.T.,
J. Gurland. 1968. ”The fracture
behavior of spheroidized carbon steels”. Transaction Quarterly 61:
156-167.
Received 10.04.2021; accepted in revised form 21.06.2021
Scientific
Journal of Silesian University of Technology. Series Transport is licensed
under a Creative Commons Attribution 4.0 International License