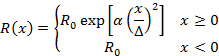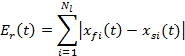Article
citation information:
Matyja, T. Safety of transport operations
performed using pallet load units. Scientific
Journal of Silesian University of Technology. Series Transport. 2021, 112, 145-156.
ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2021.112.7.12
Tomasz MATYJA[1]
SAFETY
OF TRANSPORT OPERATIONS PERFORMED USING PALLET LOAD UNITS
Summary. During transport
operations, even under normal operating conditions, the loading unit is subject
to inertial forces, which may cause deformation of the unit, and in extreme
cases, its disintegration. Stretch film wrapping is the most commonly used
method of securing a load unit. This paper presents a new simplified simulation
model of a class A load unit, with a layered structure, secured with stretch
film. Between the layers of packaging, stick-slip friction was applied. A
method of estimating the containment force was also proposed. This model can be
used to pre-determine the number of film layers necessary to ensure load
stability. Simulations can reduce the amount of film used and the number of
stability tests performed experimentally.
Keywords: transport operations, load unit stability,
stretch film
1. INTRODUCTION
Transport and storage
of widely understood goods are commonly carried out using pallet load units.
The pallet is the usually used platform for forming a load unit as a collection
of smaller packages, while wrapping with stretch film is the most frequently
used method of securing the load unit against disintegration [7].
During transport
operations, the loading unit is subject to inertial forces, which may cause
displacement of individual packages, deformation of the unit treated as a solid
and in extreme cases its disintegration. Even under normal operating
conditions, on the load unit may act acceleration with values often close to 1
g. This problem occurs in all modes of transport: road, rail, sea, air and internal
transport in warehouses [3, 8, 9, 14-16].
Stability of the load
unit (also called rigidity) is understood in literature as maintaining the
integrity of packaging included in the unit and maintaining an unchanged shape
[12]. A stable load unit, properly secured against shifting in the vehicle's
cargo space, guarantees the safety of transport operations. This problem has
been noticed in the EU [10]. Load unit stability is checked by experimental
methods. Simple static tests on an inclined plane (tilt tests) or dynamic tests
(impact tests) on specially adapted mobile platforms were carried out. Suitable
pre-stretching of the stretch film causes the appearance of force bonding the
whole load; this is called the containment force in the literature [6]. Of
course, the more layers the greater the force will be. However, the use of
excessive numbers of layers unnecessarily increases costs and negatively
affects the environment. In the literature, there are attempts to model the
dynamics of load unit containing a smaller packaging, onto the containment
force acts.
This paper presents
the author's simulation model of a loading unit secured with stretch film. This
model can be used to estimate the number of film layers necessary to ensure
load stability. Simulations can reduce the amount of film used and the number
of experimental stability tests. Such activities contribute to increased
transport safety and environmental protection. The model described below was
developed in a Matlab environment.
2. DYNAMIC MODEL OF A PALLET LOADING UNIT WITH
A LAYERED STRUCTURE
The problem of investigating the
dynamics of packages that are parts of a pallet loading unit is the complex
issue of multi-body contact (MBS) with friction. In addition, the solution of
this problem is complicated by the interaction forces between practically mass
less stretch film and packages. One way to consider the stretch film in the
load unit model is to replace it with a cloud of equidistant points connected
by springs of known stiffness [4]. At each step of the simulation, both the
positions of the packages relative to each other and the packages relative to
the point cloud should be controlled. This type of simulation requires
considerable computing power and is time-consuming.
This paper proposes a simplified
version of the class A pallet load unit model discussed in the work [11]. It is
assumed that the pallet load unit has a clearly layered structure. The class A
loading unit consists of identical rectangular packages, whose dimensions and
arrangement guarantee perfect filling of the pallet surface.
In the presented model, the method
of determining the restoring force caused by the stretch film was simplified.
Part of the force resulting from the additional stretching of the film due to
the relative displacement of the layers is ignored. Only the pre-stretching of
the film in the wrapping process is considered. Due to this, there is no need
to determining the position of the stretch film on the moved layers of the
load. This shortened the simulation time.
The assumption of a layered
structure simplifies the model and means that the layers can only move
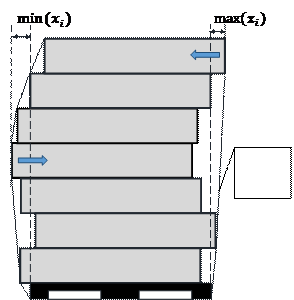
horizontally relative to each other. Figure 1 shows two successive layers and
indicates the forces that affect them. On this basis, the equations of motion
of the individual layers can be written:
|
|
|
(1) |
where: 
– mass of the layer,
– acceleration of the global system
(vehicle cargo space),
– friction force between layer i and i-1,
– the resultant reaction force of
the stretch film acting on the layer (appears from the containment force),
– displacement of the layer 
relative to the global system.
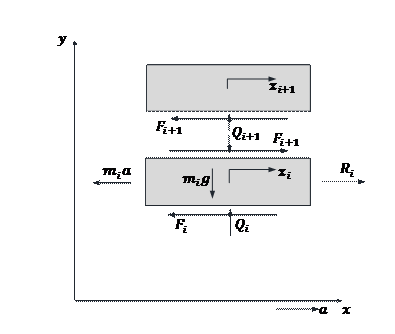
Fig. 1. Free body
diagram of the moving layers
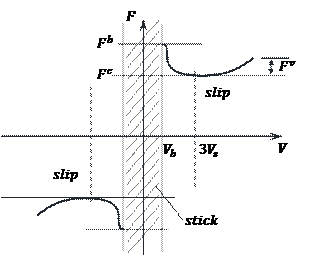
Fig. 2. The
illustrative graph of the sliding friction force in the slip-stick model
(
– speed threshold of the transition
from stick to slip, 
Stribeck speed,
– kinematic friction, 
– maximum static friction, 
– viscous friction)
Slip-stick friction was considered
in the model. When the relative velocity of the layers is lower than the
assumed very low speed of the contact break (
), then stick occurs and the force
of static friction should be determined from the condition of balance of the
upper layer relative to the lower one. However, in the case of a slip, the
friction force was determined from the formula:
|
|
|
(2) |
where: 
– kinetic friction force,
– static friction force,
– speed threshold of the Stribeck
phenomenon,
– Coulomb speed threshold,
– break speed,
– viscous friction coefficient,
– relative speed between two
selected layers.
The general ideas of the adopted
friction model are illustrated in Figure 2. The hyperbolic tangent in formula
(2) guarantees the continuity of the friction force when the relative velocity 
passes through zero and replaces the
discontinuous sign function. In the discussed model, it was assumed that [10]:
|
|
|
(3) |
|
a)
|
|
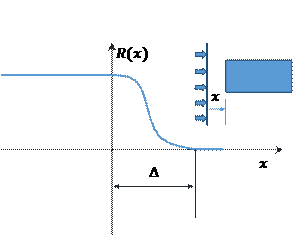
Fig. 3. Modelling of
the containment force
(a - the action of the
containment force on the most moved out layers of the load,
b - dependence of the
containment force on the distance)
In the undeformed state of the loading
unit, the containment force acts on the load uniformly from all sides.
Containment force results from properly selected pre-stretching of the film.
The model of the stretch film interaction on the load layer is illustrated in
Figure 3. When the layers of the load press on the surface of the film, the
containment force may increase. It has been assumed, however, that changes in
the stretching of the film, which will be due to the displacement of the load
layer to the left relative to the film surface, do not significantly affect the
value of the containment force. However, moving the layer away from the film
surface causes a rapid decrease of this force (Figure 3b):
|
|
|
(4) |
where: 
– nominal value of the containment
force calculated in proportion to the height of the load layer,
– assumed distance of containment
force disappearance,
– dimensionless force vanishing
factor (for example, 
),
– distance of the load layer from
the stretch film surface.
The containment force can be
estimated from the stretch film tensile test data or directly measured. Force
measurement according to ASTM D4649 using a six-inch disc seems to be of little
use in this case [6]. Measurement of the corner force using specialised
measuring equipment - for example, a transportable test load unit [13] –
will be the most advantageous. Based on the value of the edge force, the
containment force per unit of length can be determined in an elementary way.
Due to the strong adhesive properties of the stretch film and the good adhesion
of subsequent layers, it is possible to assume a proportionality of the
containment force to the number of film layers wrapping the load unit. Because
the stresses in the stretch film are very quickly relax and reduce by up to
40-50%, the measurement of force should be made after at least an hour after
wrapping the test unit with film [2].
3. NUMERICAL EXPERIMENT
The
developed simulation model was used to estimate the number of layers of stretch
film, ensuring the stability of the loading unit formed of eight layers of
packages. The basic data adopted for the simulation are summarised in Table 1.
Tab.1.
Basic data
adopted for the simulation
|
Group |
Parameter
description |
Value |
Units |
|
Loading unit |
Number
of layers |
8 |
[-] |
|
Layer
length |
1.2 |
[m] |
|
|
Layer
height |
0.2 |
[m] |
|
|
Layer
weight |
30 |
[kg] |
|
|
Friction |
Coefficient
of kinetic friction between layers (between layer and pallet) |
0.2 (0.3) |
[-] |
|
Coefficient
of increase in friction force (Stribeck
effect) |
120 |
[%] |
|
|
Breakaway
speed |
|
[m/s] |
|
|
Coefficient
of viscous friction |
|
[Ns/m] |
|
|
Containment force |
Number
of wraps |
{0,2,4,8,10} |
[-] |
|
Force
per wrap and per unit length |
85 |
[N/m] |
|
|
Distance
of containment force disappearance |
0.02 |
[m] |
Emergency
braking of a vehicle transporting a load unit with a retardation of 
during the first 
was simulated (Figure 4). The test was
carried out following EUMOS guidelines. These types of tests are usually
carried out in real conditions using special mobile platforms [13].
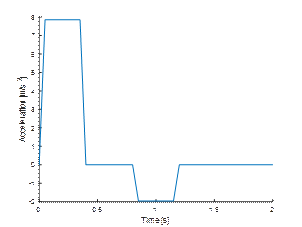
Fig. 4.
Acceleration graph during emergency braking test
4. RESULTS OF SIMULATION TESTS
Five cases were examined by simulation methods.
First, the stability of the load unit in absence of stretch film wraps was
assessed. Thereafter, stability was tested when two, four, eight and ten layers
of stretch film were used.
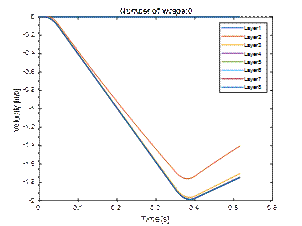
4.1. The case when stretch film was not used
Figure 5 shows the displacements and
velocities of layers of the cargo unsecured with stretch film. Due to the
increased friction between the first (bottom) load layer and the pallet, this
layer remains at rest. The model does not provide for the possibility of layers
rotation. Therefore, the simulation stops automatically when it detects a loss
of stack stability when the centre of gravity the top or several subsequent top
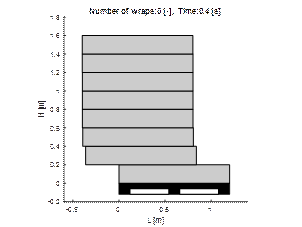
layers extend beyond their base (Figure 6).
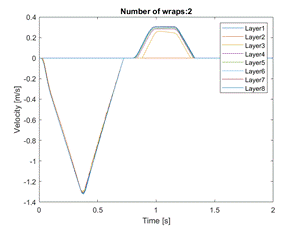
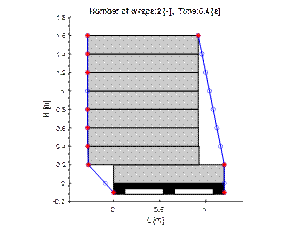
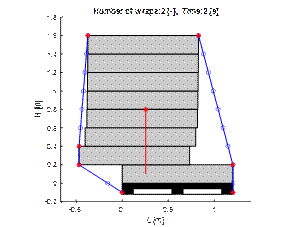
4.2. Wrapping with two layers of stretch film
Wrapping the tested loading unit
with two layers of film is insufficient, as shown in Figures 7 and 8. Although
the stack of layers maintains stability, the loading unit deforms
significantly.
|
|
|
Fig. 5. Displacements (left) and
speeds (right) of individual layers of load
|
|
|
Fig. 6. Visualisation of
displacement of layers in two moments of simulation
|
|
|
Fig. 7. Displacements and velocities
of load layers wrapped in two layers of film
|
|
|
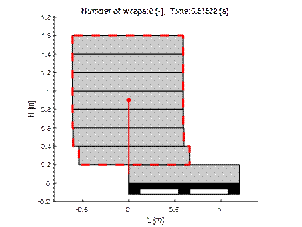
Fig. 8. Visualisation of
displacement of the load wrapped twice with film
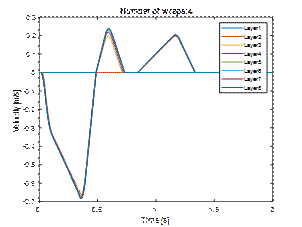
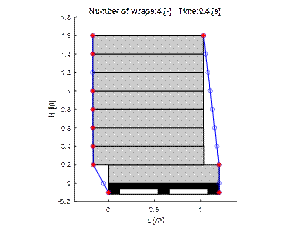
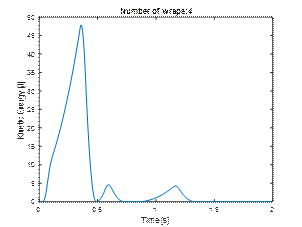
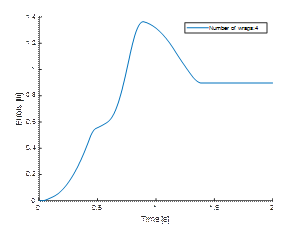
4.3.Wrapping with four layers of stretch film
|
|
|
Fig. 9. Displacements and velocities
of load layers wrapped in four layers of film
|
|
|
Fig. 10. Visualisation of
displacement of the load wrapped four times with film
Wrapping the load four times with foil reduces
layer displacement. However, displacement of the second layer by more than 10
cm is still not acceptable.
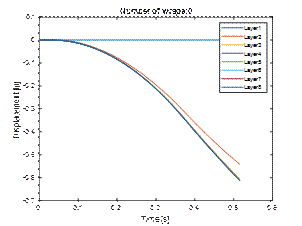
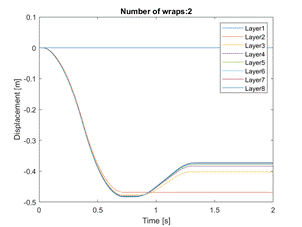
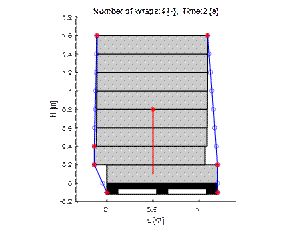
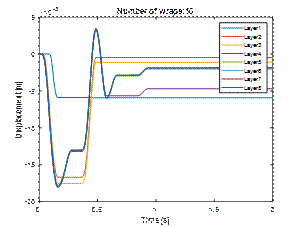
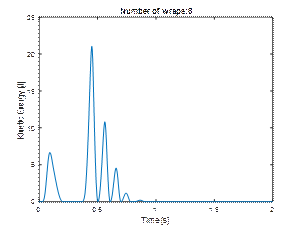
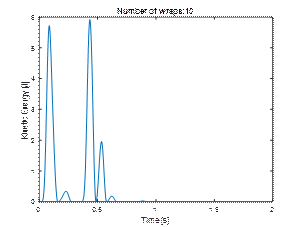
4.4. Eight and ten layers
|
|
|
Fig. 11. Comparison of displacement
of load layers for 8 and 10 wraps of film
As it results from Figure 11, the
application of 8 or 10 wraps of stretch film satisfactorily limits both the
maximum momentary displacement of the load and the final displacements. In this
case, wrapping the load eight times will be sufficient.
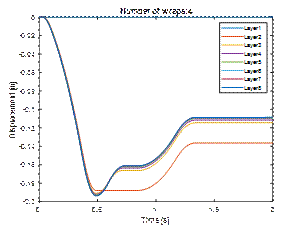
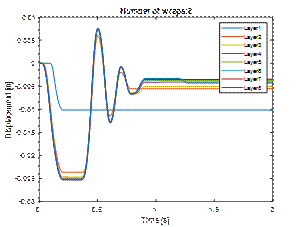
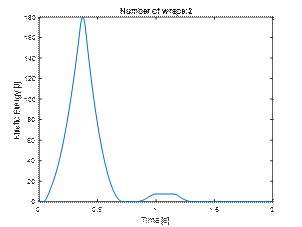
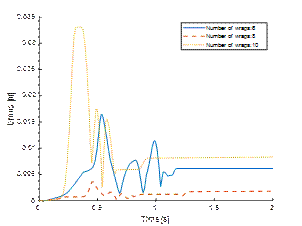
4.5. Kinetic energy as a measure of load unit stability
When assessing the stability of a
loading unit, the basic and obvious criterion is the amount of displacement. In
the case of simulation tests, it is easy to calculate another indicator in the
form of the kinetic energy of the whole unit. Comparing the results (Figure
12), one can notice a rapid decrease in the maximum values of kinetic energy
along with the increase in the number of wraps. An analysis of the kinetic energy
value shows that this decrease is of exponential nature.
However, to
use the criterion of kinetic energy in practice, it should be related to the
energy of elastic and permanent deformation of the stretch film, which requires
further research.
4.6.Results compared with the full model
If the
results of the full model [11] are taken as the reference point, then the error
of the presented simplified model can be expressed as a function:
|
|
|
(5) |
where: 
– displacement of cargo layers from
the full and simplified model, respectively; 
– number of layers.
|
|
|
|
|
|
Fig. 12. Comparison of the kinetic
energy of the load depending on the number of wraps
To
determine the error value, all simulation results from both models should be
adjusted to a constant time step, in this case 0.01 s, using linear
interpolation. When there are not enough wraps with stretch film and the layer
displacements are significant (
), the error calculated in this way
also reaches considerable values (Figure 13a). Along with the stabilisation of
the cargo, the error significantly decreases (Figure 13b), although it is not a
monotonic relationship. The change of foil stiffness with an increase in the
number of wraps changes the nature of vibrations of the load layers.
5. CONCLUSIONS
Assuming a
layered structure of the loading unit means that the results obtained based on
the model presented in this work will be coarse when the layer contains several
packages that can move relative to each other. In this case, the method of
stacking packaging, column or bricks will be important. The model, however,
guarantees results that are more accurate when the layer is one package and is
ideal for packet units (for example, a special pallet with drywall or
wood-based panels). In general, it can be argued that the better the load on
the pallet is secured by the containment force, the smaller the displacement of
the layers and the results obtained from the model are closer to the real one.
This remark similarly applies to the method chosen in the model for describing
the interaction of the stretched film with the load layers.
The main
purpose of the simulation is to estimate the value of the containment force
(indirectly the number of film layers and its initial stretching) guaranteeing
the stability of the loading unit. However, the goal is not to accurately
determine the displacement of individual layers. Therefore, the proposed model
seems to be sufficiently effective.
The
simulation tests carried out suggest that a good measure of load unit stability
assessment can be the maximum kinetic energy generated as a result of the
movement of individual layers during a standard emergency braking test. The
lower the kinetic energy, the better the load protection and stability.
|
a) |
b) |
Fig. 13. Sum of
absolute displacement errors depending on the number of wraps
References
1.
ASTM D4649. Standard Guide for Selection and Use of
Stretch Wrap Films.
2.
Bisha J. 2012. „Correlation of the
elastic properties of stretch film in unit load containment”. PhD thesis. Blacksburg, USA: Virginia
Tech.
3.
Cieśla Maria, Tadeusz Opasiak. 2014. Load
securing in cargo transport units. Katowice: PAN. ISBN: 978-83-940763-2-0.
4.
Danjou S., N. Ostergaard. 2018. “Application of
Computational MBD for Simulation of Wrap Packaging Performance”. Journal of Applied Packaging Research
10: 25-36.
5.
Directive 2014/47/EU of the European Parliament and of
the Council. O the technical roadside inspection of the roadworthiness of
commercial vehicles circulating in the Union.
6.
EUMOS 40509-2012. Test method for load unit
rigidity.
7.
Finnemore D. 2017. “Stretch wrap film and pallet
load stability”. POWDERBULK.COM. Available at: https://www.powderbulk.com/enews/2017/editorial/story_pdf/pbe_04_19_17rihf.pdf.
8.
Haniszewski T. 2017. „Modeling the dynamics
of cargo lifting process by overhead crane for dynamic overload factor
estimation”. Journal of Vibroengineering 19(1): 75-86.
9.
Kuskil’din R.B., M.A. Vasilyeva. 2017. „Dynamic loads during
safety braking of the container with cargo”. Procedia Engineering
206: 248-253. DOI: https://doi.org/10.1016/j.proeng.2017.10.469.
10.
MATLAB Documentation. Friction in contact between
moving bodies. Available at https://www.mathworks. com.
11.
Matyja T. 2020. „Assessment of the
pallet unit load stability by simulation methods”. Communications - Scientific Letters of
the University of Žilina 22(3): 19-28.
12.
Singh J., K. Saha, T. Sewell. 2017. „Evaluation of
Stability of Unit Loads for Tilt and Shock Events During Distribution”. Journal
of Applied Packaging Research 9(3):73-93.
13.
The Transportable Test Pallet. Available at:
https://www.bestpackaging.com.au/.
14.
Vlkovský M., M. Šmerek, J.
Michálek. 2017. „Cargo Securing During
Transport Depending on the Type of a Road”. IOP Conf. Series: Materials Science and Engineering 245:
042001. DOI: 10.1088/1757-899X/245/4/042001.
15.
Vukić Luka, Helena Ukić Boljat, Merica
Slišković. 2018. “Short Sea Shipping
– an Opportunity for Development of the North Port of Split”. Nase More 65(3): 18-25.
16.
Wiśnicki Bogusz, Adrianna Dyrda. 2016.
“Analysis of the Intermodal Transport Efficiency in the Central and
Eastern Europe”. Nase More 63(2):
43-47.
Received 03.04.2021; accepted in revised form 30.06.2021
Scientific
Journal of Silesian University of Technology. Series Transport is licensed
under a Creative Commons Attribution 4.0 International License