Article citation information:
Soatova, N. Calculation
of flexible bending elements of a flight structure given their actual condition.
Scientific Journal of Silesian University
of Technology. Series Transport. 2021, 110,
115-123. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2021.110.10.
Nodira SOATOVA[1]
CALCULATION
OF FLEXIBLE BENDING ELEMENTS OF A FLIGHT STRUCTURE GIVEN THEIR ACTUAL CONDITION
Summary. This article presents
the results of the analysis of experimental data on testing of reinforced
concrete elements for multiple-repeated loads and field tests of operated span
structures. This article proposes dependencies on the definition of deflections
during the operation period. Based on the processing of the available
experimental data, dependences are proposed for determining deflections under
multiple repeated loads, and on this basis, dependences are obtained for
predicting the residual life of span elements. The initial data for the
calculations are the data on the accumulated residual deflections
determined in the process of technical diagnostics.
Keywords: resource
impact of corrosion, span structures, deflections, reinforced concrete
elements, calculation method
1.
INTRODUCTION
In many countries of the world, special importance is attached to
scientific research in the field of studying the effect of corrosion of
reinforcement and concrete. Improving both quality indicators and methods for
calculating durability and strength, extending the service life of transport
facilities. In this direction, in particular, improving the calculations of the
resource impact of corrosion of concrete and reinforcement of bridge span
structures, the development of calculation methods for using modern computer
technologies in scientific research is considered one of the important tasks [1,3-5,12,13].
With the acquisition of independence of the Republic of Uzbekistan,
great importance was attached to the development of transport communications
structures, the design of ground structures, and the improvement of their
construction and operation.
Currently, more than 7000 bridges are operated in the Republic. To
increase their reliability and calculate their strength, several tasks were
performed. Along with this, it is necessary to improve the methods of
calculation and increase the resource of artificial structures in the structure
of transport communications. The Strategy for Action for the Further
Development of the Republic of Uzbekistan, included the following objectives,
“... the implementation of targeted programs for the development and
modernisation of road transport, engineering, communication and social
infrastructures”. In a broad sense, the importance of a research and
development approach to calculating the life of road bridges in this respect,
increasing operational reliability and ensuring the reliability of newly
erected and operated bridges grows.
2. FORECASTING RESIDUAL RESOURCE BY DEFLECTION
When assessing the load capacity and predicting the residual life of
reinforced concrete spans, residual deflection (sagging) must be considered,
and in many cases, this factor may be decisive.
As a result of the analysis of experimental data on tests of reinforced
concrete elements for repeated loads and field tests of operated span
structures, dependencies are proposed for defining deflections during
operation. The results of the survey of reinforced concrete spans showed that
the actual accumulated deflections (sagging) differ from the calculated. The
calculation was according to the design standards of the year of construction
of the objects under consideration. The use of existing standards has however
not led to satisfactory results. This is clearly observed when calculating the
deflections of the console of the plates of the extreme beams of the road
bridges and the external console of the ballast trough plates in the railway
bridges. Here, the difference between the actual and calculated deflections
reaches 4-5 times [6,7]. In connection with the foregoing, an attempt was made
to improve the existing methodology for calculating deflections.
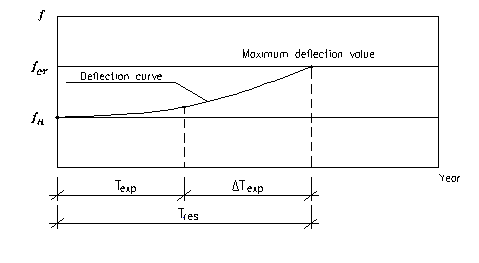
Fig. 1. Prediction of residual resource on the criterion of limiting
deflection
Texp - time from the start of operation until the time of the survey; Tres is a complete
resource; Δ Tres - residual resource
Simultaneously, the total value of the deformation of the residual
deflections of bending reinforced concrete elements, considering long-term
constant and frequently repeated loads, is presented in the form:
f = fg+fN (1)
where:
fg - deflection
from the effects of permanent long-acting loads;
fN - deflection from repeated exposure to temporary loads.
The value of fg is
determined by known methods [6] considering the creep of concrete under the
action of a constant load. Moreover, as shown in [11], for bending reinforced
concrete beams under constant long-acting loads, in natural climatic
conditions, formulas of normative documents, considering creep deformation of
concrete according to recommendations [14], give satisfactory results.
The deflections of reinforced concrete beams due to the long action of
multiple-repeated loads are manifested due to the deformation of the
vibro-creeping concrete. According to V.M. Bondarenko [2], the additional
increment of the deflection in dynamically loaded structures due to the
vibrocreep of concrete can reach significant values.
Below, an attempt is made to develop a practical method for determining
the deflection of the dynamic component of the load based on the available
experimental data [15]. This paper uses the results of experimental studies
performed in TashIIT laboratory [15]. The test results of beams for multiple
loadings are shown in Fig. 2. As can be seen in Fig. 2, a clear pattern of
changes in deflections during repeated loads depends on the voltage level.
Beams loaded with a high level of stress have high values of relative
deflection at repeated loads.
The determination of the expected limit values of residual deflections
during repeated loads is carried out by constructing diagrams according to the
procedure [6] (Fig. 3). To do this, we calculate the increment N/f, where N is the number of loading
cycles; f is the value of residual deflection corresponding to this magnitude
of loading cycles. On the diagram, we plot N/f
along the ordinate axis and N values
along the abscissa axis. From the obtained points, a regression line is plotted
graphically or analytically, the cotangent of which angle is taken as the
limiting deformation value of the residual deflection fcr, N, and the section cut off by this straight line at abscissa
axis, for the parameter of the rate of increase in the deflection deformation.
The limiting values fg- of curvature from constantly repeated loading can be determined by the
dependence:
(2)
where:
εbNcr - limit values of deformation from constantly repeated loading; l is the
length of the span;
CfNcr - limiting values of a measure of a vibrocreep of concrete;
x - height of the
compressed zone of concrete.
The limiting values of the vibro-creep measure are recommended to be
determined by the expression [6]:
(3)
where:
φcr(t,τ0) - the limiting values of the
characteristic of simple creep of concrete;
ρ - asymmetry of loading cycles;
Ncr - the limit number of cycles until the deflection of permissible values
is reached.
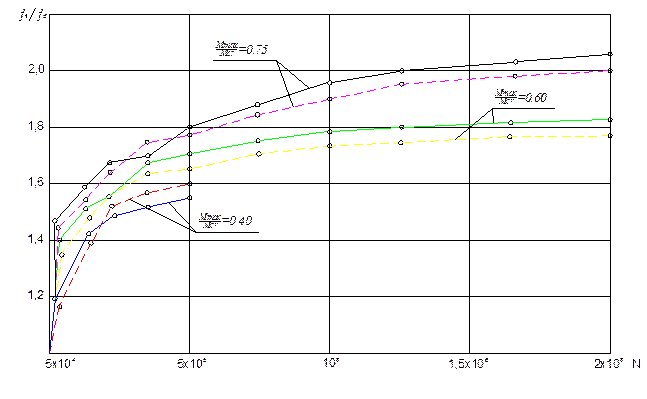Fig. 2. The increase in the
relative deflection of beams with
multiple repeated loads
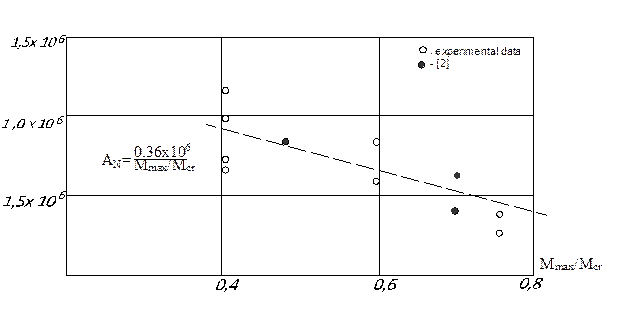Fig. 3. The change in af depending on the level of loading Mmax/MCr
The limiting deflection from constantly repeated loading is determined
by the known formula:
(4)
According to the parameters obtained above, it is possible to determine the
value of the deflection fN
for any number of loading cycles N by
the formula:
(5)
In the formula, the parameter af
characterises the rate of accumulation of residual deflection under
repeated loading and depends on many factors. The change in aN determined from the
results of processing the experimental data shown in Fig. 3, depending on the
loading level of the beam Mmax/Mcr.
The change in the af parameter from Mmax/Mcr is satisfactorily described by the
expression:
(6)
Perhaps there is a connection from the asymmetry of the loading cycle,
the mechanical characteristics of concrete and other factors. However,
according to the available experimental data, such a link cannot be
established. In the calculations, the number of loading cycles according to the
actual throughput of the overpass is determined by this method [6]. For
practical calculations, the increase in deflections over time can be
established using the relationship:
(7)
From here:
(8)
Combining formulas,
we get:
(9)
where:
Ncr - the number of loading cycles until the deflection of fcr is reached;
Tres - the service life of the superstructure.
According to the obtained dependence, it is possible to determine the
amount of deflection from the impact of a long-term load during operation. Full deflection for
bending beams:
(10)
For the outer console slab:
(11)
3. CONCLUSIONS
Thus, based on the processing of the available experimental data,
dependencies are proposed for determining deflections under multiple-repeated
loading and are obtained on this basis for predicting the residual life of
elements of span structures [15]. The initial data for the calculations are the
data on the accumulated residual deflections determined in the process of
technical diagnostics.
Furthermore, it was established that one of the main factors that reduce
the carrying capacity and residual life of elements of the superstructures is
the accumulation of residual sags (sagging). It is shown that the main reason
for the development of unacceptable deflections is the constant build-up of the
carriageway with asphalt concrete pavement and salt corrosion of concrete and
reinforcement.
References
1.
Balevičius R. 2005. “Semi analytical
modelling of reinforced concrete members in bending”.Mechnika 5(55): 32-40.
2.
Bondarenko V.M., L.I. Iosilevsky, V.P. Chirkov. 1996. Reliability of building structures and
bridges. Moscov: Publishing House of the Academy of Architecture and
Construction.
3.
Dell'Acqua, Gianluca, Mario De Luca, Carlo Giacomo
Prato, Olegas Prentkovskis, Raimundas Junevicius. 2016. „The impact of
vehicle movement on exploitation parameters of roads and runways: a short
review of the special issue”. Transport
31(2) Special Issue: 127-132.
4.
Kliukas R., R. Kačianauskas. 2005.
“Comparison of global and local damage in reinforced concrete columns
specimens”. Mechnika 4(54):
30-37.
5.
Krayushkina
Kateryna, Olegas Prentkovskis, Andrii Bieliatynskyi, Raimundas Junevičius. 2012. “Use of steel slags in automobile
road construction”. Transport
27(2): 129-137.
6.
Mamazhanov R. 1989. “Prediction of the process
of damage accumulation in elements subject to regime loads”. Bulletin of the Academy of Sciences of
Uzbekistan. Series of technical sciences 2: 22-25.
7.
Mamazhanov R.K., R.Z. Nizamutdinova, O.I. Kildeva.
1996. “Results of inspection of railway reinforced concrete
bridges”. Materials of the
International Scientific and Technical Conference. Tashkent Automobile and
Road Institute. P. 102-105.
8.
Mazurkiewicz D. 2010. „Tests of extendability
and strength of adhesive-sealed joints in the context of developing a computer
system for monitoring the condition of belt joints during conveyor
operation”. Eksploatacja i
Niezawodnosc – Maintenance and Reliability 3: 34-39.
9.
Mazurkiewicz D. 2014. „Computer-aided
maintenance and reliability management systems for conveyor belts”. Eksploatacja i Niezawodnosc –
Maintenance and Reliability 16(3): 377-382.
10. Michalski R., S.
Wierzbicki. 2008. „An analysis of degradation of vehicles in
operation”. Eksploatacja i
Niezawodnosc – Maintenance and Reliability 1: 30-32.
11. Nizamutdinova R.Z.
1994. “Resource of reinforced concrete bridge spans on the railways of an
industrial enterprise”. Tashkent Institute of Railway Engineers. Thesis for the degree of candidate of
technical sciences 05.23.15. Tashkent.
12. Pokorny P., D.
Dobias, M. Vokac. 2016. “Bond strength of hot - dip galvanized
reinforcement (B500B) with concrete”. Metalurgija
55(3):
337-340.
13. Pokorny P., P. Tej,
P. Szelag. 2016. “Chromate conversion coatings and their current
application”. Metalurgija
55(2): 253-256.
14. Recommendation for evaluating and ensuring the
reliability of vehicles. Moscov: TSNISK. 1989.
15. Saatova N.Z. 2019.
“The method of calculating the deflections of the bent elements of the
superstructure taking into account the actual state at the time of technical
diagnostics”. XXXXIII International Scientific And
Practical Conference. St. Petersburg. P. 89-96.
Received 01.08.2020; accepted in revised form 30.10.2020
Scientific Journal
of Silesian University of Technology. Series Transport is licensed under a Creative
Commons Attribution 4.0 International License