Article
citation information:
Kirschenstein, M., Krasuski, K.,
Goś, A. Methods
of precise aircraft positioning in the GPS system with an application of the
troposphere correction. Scientific
Journal of Silesian University of Technology. Series Transport. 2020, 109, 73-84. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2020.109.7.
Małgorzata KIRSCHENSTEIN[1], Kamil
KRASUSKI[2],
Artur GOŚ3
METHODS
OF PRECISE AIRCRAFT POSITIONING IN THE GPS SYSTEM WITH AN APPLICATION OF THE
TROPOSPHERE CORRECTION
Summary. This article presents
the results of studies concerning the designation of accuracy in aircraft
navigation positioning by means of the SPP and the SBAS code methods. The
examination of the aircraft positioning accuracy was made in the aspect of the
use of tropospheric correction in observation equations of the SPP and the SBAS
positioning methods. The accuracy of the coordinates of the aircraft in the SPP
and the SBAS solutions was referenced to the DGPS reference solution. The
investigations were conducted on raw observation data and GPS navigation data
in an air test in Dęblin. Based on the conducted calculations, it was
proved that the lack of use of tropospheric correction in the SPP method causes
an error in an aircraft position up to 18.5 m, and in the SBAS method up to
23.2 m. In addition, the statistical measure of RMS accuracy in the absence of
applying the tropospheric correction in the SPP method results in an accuracy
decrease to 8.6 m, and in the SBAS method to 12.2 m, accordingly.
Keywords: GPS system, troposphere correction, SPP method,
SBAS method, DGPS method, accuracy
1. INTRODUCTION
Along with the use of GPS satellite technology in
aviation, there has been a rapid increase in the methods of aircraft precise
positioning in the area of air navigation. The methods of aircraft positioning
for GPS satellite technology can be divided into absolute methods
(non-differential) and differential methods (relative) [16]. Moreover, among
the absolute and differential methods, both code and phase observations of GPS
measurements are exploited [3]. In addition, the absolute and differential
positioning methods may be single- frequency, dual-frequency or multi-frequency
[8].
The basic method of GPS positioning in aviation is a
construction of observation equations, elimination or modelling of systematic
errors as well as determining unknown parameters. The most common methods of
GPS positioning in aviation are as follows: SPP code method [7], SBAS
positioning method [4] and the DGPS differential method [5]. In the SPP code
method, the determined parameters are the aircraft position and the GPS receiver
on-board clock. The modelled parameters are satellite-receiver geometric
distance, satellite clock error, ionospheric and tropospheric correction,
relativistic correction, TGD hardware delay and a multipath effect [15]. The
method of positioning designated SBAS parameters are also the position of the
aircraft and the GPS receiver clock error. Furthermore, the modelled parameters
are as well: the geometric distance satellite-receiver, satellite clock error,
tropospheric and ionospheric correction, relativistic correction, TGD hardware
delay and a multipath effect. It should be emphasised that the coordinates of
the GPS satellite, the GPS satellite clock error, tropospheric and ionospheric
correction are modelled by means of the SBAS correction algorithms [4]. In the
DGPS positioning method, the determined parameters are finally the aircraft
position and the clock difference of a GPS on-board receiver as well as a GPS
receiver mounted on the reference station. Then, the modelled parameters are
similarly: the satellite-receiver geometric distance, tropospheric and
ionospheric correction and a multipath effect. However, the satellite clock
error, relativistic correction and TGD hardware delay are eliminated from the
observation equations by applying the differentiation operator [1].
Within this
work, the authors intend to present the research results of aircraft
positioning accuracy in the aspect of using the tropospheric correction in the
navigation calculations. The position of the aircraft will be determined based
on the SPP code method in the GPS system, the SBAS method for EGNOS
corrections, and the DGPS differential method. This work explains how a
systematic error in the form of the tropospheric correction affects the
accuracy of aircraft positioning for the abovementioned three methods of
satellite positioning in air navigation. The examination exploits real GPS data
from an on-board receiver and a ground reference station. The recorded data
were used for numerical calculations in the RTKLIB v.2.4.2. programme and to
develop the results in the Scilab v.6.0.0. programme.
2. RESEARCH
METHODOLOGY
A mathematical model to determine the position of the
aircraft in the SPP code method, in the GPS system, can be described as below
[12]:
(1)
where:
-
code measurement (pseudorange) registered by the airborne receiver in the GPS
system,
-
the geometric distance satellite and the airborne receiver in the GPS system,
,
- satellites coordinates in the GPS system,
- aircraft coordinates in the geocentric XYZ
frame,
-
speed of light,
- receiver clock bias,
- satellite clock bias,
- ionosphere correction,
- troposphere correction,
- relativistic correction,
- timing group delay,
- multipath effect.
The mathematical
model of the aircraft position determination in the SBAS method for EGNOS
corrections can be described as below [10]:
(2)
where:
-
code measurement (pseudorange) registered by the airborne receiver in the GPS
system,
-
the geometric distance satellite and the airborne receiver in the GPS system,
after long-term EGNOS correction,
,
- satellites coordinates in the GPS system,
after long-term EGNOS correction,
- aircraft coordinates in the geocentric XYZ
frame,
-
speed of light,
- receiver clock bias,
- satellite clock bias, after long-term EGNOS
correction,
- ionosphere correction, based on GRID SBAS
model,
- troposphere correction, based on RTCA-MOPS
SBAS troposphere model,
- relativistic correction,
- timing group delay,
- multipath effect,
- fast EGNOS correction.
The mathematical
model of determining the aircraft position in the DGPS differential method in
the post-processing mode can be described as below [2]:
(3)
where:
- difference
between pseudorange registered by the airborne receiver and reference station
in the GPS system,
-
difference between geometric distance: satellite-airborne receiver, and
satellite-reference station in the GPS system,
-
speed of light,
- difference between airborne receiver clock
bias and reference station receiver clock bias,
- difference between ionosphere correction for
airborne receiver and reference station,
- difference between troposphere correction for
airborne receiver and reference station,
- difference between multipath effect for
airborne receiver and reference station.
3. THE RESEARCH
EXPERIMENT
In
the examination test, scientific examinations were conducted to determine the
accuracy of aircraft positioning in the aspect of exploiting the tropospheric
correction in navigation computations. The aircraft position was determined given
the SPP code method, the SBAS positioning method, and the DGPS differential
method in post-processing. In the calculations, to determine the accuracy of
aircraft positioning, a comparison between the designated coordinates in the
SPP vs. DGPS and SBAS vs. DGPS solutions was made. Within the SPP and the SBAS
method, the authors obtained two SBAS positioning solutions: the former
included the tropospheric correction, whereas the latter disregarded the
tropospheric correction. In the DGPS solution, the authors considered the
tropospheric correction. Furthermore, the designated aircraft position in the
DGPS solution is a reference position for the performed calculations. The SPP
method model had the tropospheric correction model used as Saastamoinen model [9].
In the SBAS solution, the authors used a model of the tropospheric correction
as the RTCA MOPS-SBAS model [11]. Then, in the DGPS solution, the authors used
a model of the tropospheric correction as the Saastamoinen model. The
calculations were made in the RTKLIB v.2.4.2 programme [17]. The calculations
are based on the GPS data derived from the on-board receiver mounted in a
Cessna 172. The data comes from a test flight over Dęblin. Moreover, in
the DGPS differential method, the authors used the data derived from the GPS
receiver mounted on the reference station in Dęblin. The SBAS method used
corrections from the EGNOS S120 satellite. The calculations performed with an
interval and time synchronisation were equal to 1 s. In addition, the
remaining comparative analyses were performed in the Scilab v.6.0.0 programme
[18].
In
the first stage of the research, the authors determined the position of the
Cessna 172 for the SPP method, twice: initially with the tropospheric
correction, and later without its use. In the second stage of the research, it
was possible to designate the position of the Cessna 172, first, for the SBAS
method, and second, without it. In
the next step, the authors designated the reference position of the Cessna 172
for the DGPS differential method, using the tropospheric correction. The
accuracy analysis is presented in section 4.
4.
RESULTS
The analysis
of accuracy was made to compare the designated aircraft coordinates in the SPP,
SBAS and DGPS solutions. The comparative analysis was performed for geocentric
XYZ aircraft coordinates. In the second stage, the authors specified the
accuracy of coordinates of the aircraft in the SPP code solution, as below [6]:
(4)
where:
- obtained aircraft coordinates from Equation 1,
- obtained aircraft coordinates from Equation 3.
Furthermore,
for the results of Equation 4, the authors determined
a statistic quantity, which determines the positioning accuracy in the form of
RMS parameter, as below [13]:
(5)
where:
- number measurement epochs.
In
the second stage, the authors specified the accuracy of aircraft coordinates in
the SBAS code solution, as below [6]:
(6)
where:
- obtained aircraft coordinates from Equation 2,
- obtained aircraft coordinates from Equation 3.
Furthermore,
for the results of Equation 6, the authors determined
a statistic quantity, which determines the positioning accuracy in the form of
RMS parameter, as below [13]:
(7)
where:
- number measurement epochs.
Fig.
1 shows the results of the aircraft positioning accuracy using the SPP code
method. The results in Fig. 1 considers the impact of the tropospheric
correction in the process of computing the position of the aircraft in the SPP
method. The aircraft positioning accuracy along the X-axis ranged from -4.2 to
+3.4 m. Next, the aircraft positioning accuracy along the Y-axis ranged from
-1.5 to +1.2 m. In addition, the accuracy of aircraft positioning along the
Z-axis ranged from -1.7 to +2.2 m. It is worth emphasising that the average
positioning accuracy is equal to +0.4 m along the X-axis, +0.2 m along the
Y-axis, and +0.1 m along the Z-axis.
Fig.
2 shows the results of the aircraft positioning accuracy using the SPP code
method. The results in Fig. 2 do not consider the effect of the tropospheric
correction in the computational process of the aircraft position in the SPP
method. The aircraft positioning accuracy along the X-axis ranged from -1.1 to
+15.6 m. Next, the aircraft positioning accuracy along the Y-axis ranged from
-0.1 to +6.9 m. In addition, the accuracy of aircraft positioning along the
Z-axis ranged from +4.5 to +18.5 m. It is worth to note that the average
positioning accuracy is equal to +7.7 m along the X-axis, +2.3 m along the
Y-axis, and +8.4 m along the Z-axis.
Fig. 3 shows the results of the aircraft
positioning accuracy using the SBAS code method. The results in Fig. 1 do not
include the effects of the tropospheric correction in the computational process
of the aircraft in the SBAS positioning method. The aircraft positioning
accuracy along the X-axis ranged from +2.0 to +6.9 m. Next, the aircraft
positioning accuracy along the Y-axis ranged from -1.0 to +0.5 m. In addition,
the accuracy of aircraft positioning along the Z-axis ranged from +1.1 to +5.7
m. It is imperative to note that the average positioning accuracy is equal to
+3.9 m along the X-axis, -0.3 m along the Y-axis, and +3.2 m along the Z-axis.
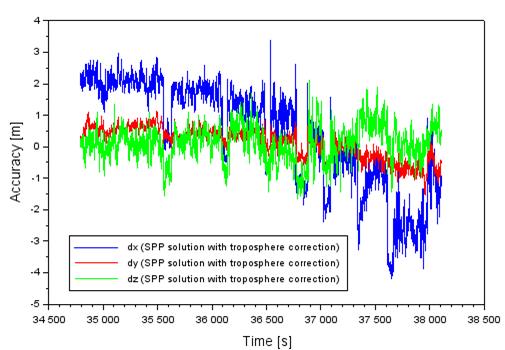
Fig. 1. The accuracy of aircraft
position based on the SPP solution with troposphere correction [Source: Based
on Scilab software]
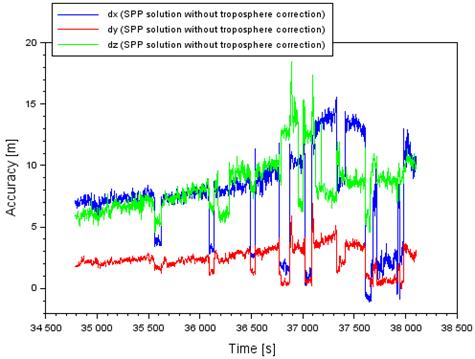
Fig. 2. The
accuracy of aircraft position based on the SPP solution without troposphere
correction [Source: Based on Scilab software]
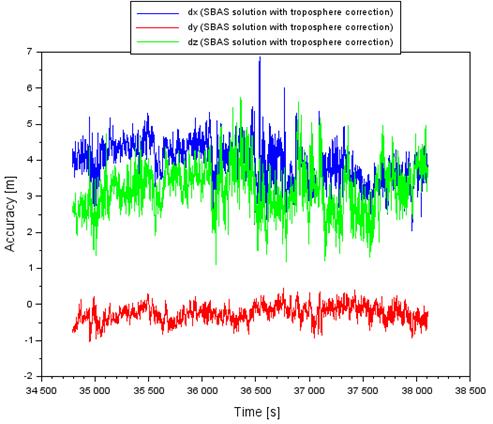
Fig. 3. The
accuracy of aircraft position based on the SBAS solution with troposphere
correction [Source: Based on Scilab software]
Fig.
4 shows the results of the aircraft positioning accuracy using the SBAS
positioning method. The results in Fig. 1 do not include the impact of the
tropospheric correction in the process of computing the position of the
aircraft in the SBAS positioning method. The aircraft positioning accuracy
along the X-axis ranged from +4.8 to +18.5 m. Next, the aircraft positioning
accuracy along the Y-axis ranged from -0.6 to +5.2 m. In addition, the accuracy
of aircraft positioning along the Z-axis ranged from +7.2 to +23.2 m. It is of
considerable note that the average positioning accuracy is equal to +9.9 m
along the X-axis, +1.4 m along the Y-axis, and +11.8 m along the Z-axis.
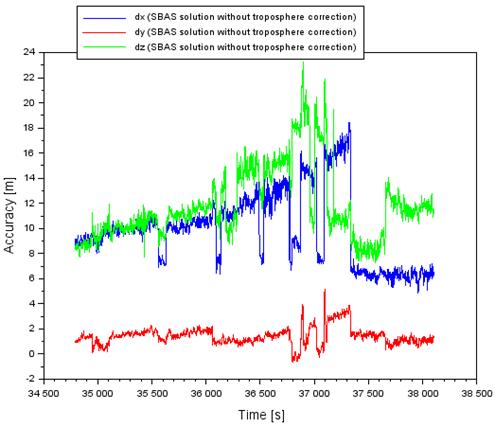
Fig.
4. The accuracy of aircraft position
based on the SBAS solution without troposphere correction [Source: Based on
Scilab software]
Figs.
5 and 6 illustrate the results of 3D-error aircraft position in a 3D plane. The
shift value of the designated aircraft position in the SPP and the SBAS
solutions against the reference position determined by the DGPS technique is
defined as follows [14]:
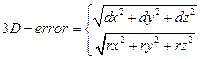(8)
The
values of the 3D-error parameter for the SPP method range from 0.1 to 4.4 m,
using the troposphere correction in navigation computations for the aircraft
position. The 3D-error parameter values for the SPP method range from 4.7 to
22.4 m, when the tropospheric correction is not included in the navigation
computations of the aircraft position. The 3D-error parameter value for the
SBAS method ranges from 2.6 to 8.0 m, using the tropospheric correction in the
navigation calculations of the aircraft position. Moreover, the values of the 3D-error
parameter for the SBAS method range from 9.2 to 28.1 m, when the tropospheric
correction is not included in navigation computations of the aircraft position.
Based on the 3D-error parameter findings, it can be observed that disregarding
the tropospheric correction in calculations results in massive degradation of
an aircraft position against the reference trajectory, for example, even up to 22.4
m in the SPP method and 28.1 m in the SBAS method, respectively. Therefore, it
can be concluded that the tropospheric correction is of huge importance in
determining an aircraft position during flight operations.
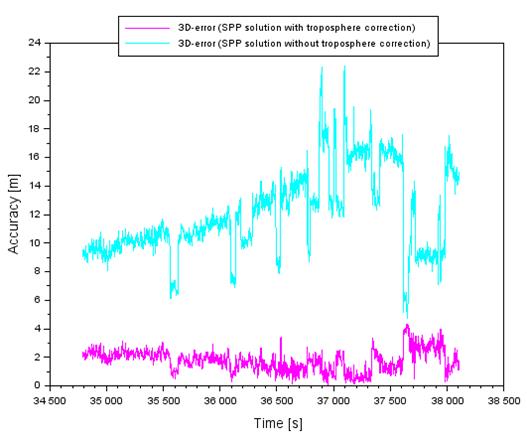
Fig.
5. The values of 3D-error of aircraft
position accuracy based on the SPP solution [Source: Based on Scilab software]
Tab. 1
Comparison
of obtained RMS parameter [Authors’ study]
|
Positioning method |
RMS along to X-axis [m] |
RMS along to Y-axis [m] |
RMS along to Z-axis [m] |
|
SPP
(with troposphere correction) |
1.7 |
0.5 |
0.6 |
|
SPP
(without troposphere correction) |
8.4 |
2.6 |
8.6 |
|
SBAS
(with troposphere correction) |
4.0 |
0.3 |
3.2 |
|
SBAS
(without troposphere correction) |
10.4 |
1.6 |
12.2 |
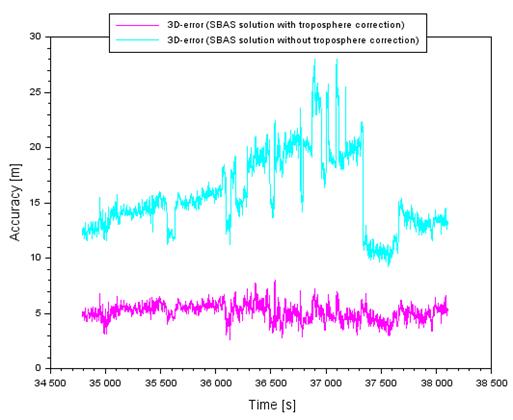
Fig.
6. The values of 3D-error of aircraft
position accuracy based on the SBAS solution [Source: Based on Scilab software]
Tab.
1 shows the results of accuracy in the form of the statistical parameter RMS,
in accordance with Equations 5 and 7. It can be observed that disregarding the
tropospheric correction in the SPP method and the SBAS method causes
significant degradation of the aircraft position. In the SPP method, the lowest
RMS accuracy equals 1.7 m, using the tropospheric correction in the observation
model. Next, the lack of troposphere correction in the SPP method causes
degradation in aircraft position accuracy, even to the level of 8.6 m. In the
SBAS method, the lowest RMS accuracy equals 4.0 m when using the tropospheric
correction in the observation model. Besides, the lack of tropospheric
correction in the SBAS method leads to the degradation of aircraft position
accuracy, even to the level of 12.2 m.
5.
CONCLUSION
This
paper demonstrates the results of research into the aircraft positioning
accuracy by means of the SPP, SBAS and DGPS methods. In particular, the study
focuses on examining the impact of the tropospheric correction on aircraft
positioning accuracy in air navigation. In practice, this work presents
research tests showing how the use of the tropospheric correction in the SPP
and the SBAS methods affect the accuracy of determining aircraft coordinates.
The study uses real observation and GPS navigation data derived from an
experimental air test made by the Cessna 172. Based on the conducted
calculations, it was found that:
-
the lack of use of the tropospheric correction in the
SPP method results in a drop in accuracy of determining the XYZ aircraft
coordinates even to the level of 18.5 m;
-
the lack of use of the tropospheric correction in the
SBAS method results in a drop in accuracy of determining the XYZ aircraft
coordinates even to the level of 23.2 m;
-
the lack of use of the tropospheric correction in the
SPP method results in a rise in the RMS error to the level of 8.6 m;
-
the lack of use of the tropospheric correction in the
SBAS method results in a rise in the RMS error to the level of 12.2 m.
The
obtained research findings, in the work, indicate that the systematic error in
the form of the tropospheric correction exerts a tremendous influence on the
designation of an aircraft position. Furthermore, ignoring the systematic error
in an observational equation of determining the aircraft position may cause large
degradation of accuracy in the designated coordinates of a moving object in air
navigation. Hence, it is important to make a correct interpretation of
observational equations in a given method for determining the position of a
moving object in the aspect of modelling systematic errors.
Acknowledgements
This paper was supported
by the Military
University of Aviation in 2020.
References
1.
Bakuła M. 2007.
“Static Network Code DGPS Positioning vs. Carrier Phase Single Baseline
Solutions For Short Observation Time and Medium-Long Distances”. Artificial Satellites 42(3): 167-183.
DOI: 10.2478/v10018-008-0009-9.
2.
Bakuła M. 2010.
“Network code DGPS positioning and reliable estimation of position
accuracy”. Survey Review
42(315): 82-91. DOI: 10.1179/003962610X12572516251448.
3.
Bosy J. 2005. “Precise
processing of satellite GPS observations in local networks located in mountain
areas”. Zeszyty Naukowe Akademii
Rolniczej we Wrocławiu 522. ISSN: 0867-7964.
4.
Ciećko A. 2019.
“Analysis of the EGNOS quality parameters during high ionosphere
activity”. IET Radar, Sonar &
Navigation 13(7): 1131-1139. DOI: 10.1049/iet-rsn.2018.5571.
5.
Grzegorzewski M., W.
Jaruszewski, A. Fellner, S. Oszczak, A. Wasilewski, Z. Rzepecka, J.
Kapcia, T. Popławski. 1999. “Preliminary results of DGPS/DGLONASS
aircraft positioning in flight approaches and landings”. Annual of Navigation 1: 41-53.
6.
Grzegorzewski M. 2005.
“Navigating an aircraft by means of a position potential in three
dimensional space”. Annual of
Navigation 9: 1-11.
7.
Grzegorzewski M., A.
Ciećko, S. Oszczak, D. Popielarczyk. 2008. “Autonomous and EGNOS
positioning accuracy determination of cessna aircraft on the edge of EGNOS
coverage”. Proceedings
of the 2008 National Technical Meeting of the Institute of Navigation. San Diego, CA. January 2008. P. 407-410.
8.
Hofmann-Wellenhof B., H.
Lichtenegger, E. Wasle. 2008. GNSS
– Global Navigation Satellite Systems: GPS, GLONASS, Galileo and More.
Springer Wien NewYork, Wien, Austria. ISBN: 978-3-211-73012-6.
9.
Kleijer F. 2004. Troposphere Modeling and Filtering for
Precise GPS Leveling. PhD thesis. Department of Mathematical Geodesy and
Positioning, Delft University of Technology. Kluyverweg 1, P.O. Box 5058, 2600 GB DELFT, the
Netherlands. 260 p.
10.
Li L., Jia C., Zhao L., Cheng J., Liu J., Ding J.
2016. “Real-time single frequency precise point positioning using SBAS
corrections”. Sensors 16(8).
DOI: 10.3390/s16081261.
11.
MOPS. 1998. Minimum
operational performance standards for global positioning system/wide
area augmentation system airborne equipment. Document No. RTCA/DO-229A,
June 8, 1998, prepared by SC-159.
12.
Pan L., C. Cai, J.
Zhu, X. Cui. 2019. „Kinematic absolute
positioning with quad-constellation GNSS”. Kinematics - Analysis and Applications. Joseph Mizrahi, IntechOpen.
DOI: 10.5772/intechopen.86368. Available in:
https://www.intechopen.com/books/kinematics-analysis-and-applications/kinematic-absolute-positioning-with-quad-constellation-gnss.
13.
Przestrzelski P., M.
Bakuła. 2014. “Performance of real time network code DGPS services
of ASG-EUPOS in North-Eastern Poland”. Technical Sciences 17(3): 191-207.
14.
Rodríguez-Bilbao I.,
S. M. Radicella, G. Rodríguez-Caderot, M. Herraiz. 2015. “Precise
point positioning performance in the presence of the 28 October 2003 sudden
increase in total electron content”. Space
Weather 13: 698-708. DOI: 10.1002/2015SW001201.
15.
Sanz Subirana J., Juan
Zornoza J.M., Hernández-Pajares M. 2013. GNSS Data Processing. Vol.
I: Fundamentals and Algorithms. Publisher: ESA Communications, ESTEC,
Noordwijk, Netherlands. ISBN: 978-92-9221-886-7. ESA TM-23/1.
16.
Seeber G. 2003. Satellite
Geodesy – 2nd completely revised and extended edition. Walter de
Gruyter GmbH & Co. KG, 10785 Berlin, Germany. ISBN: 3-11-017549-5.
17.
Takasu T. 2013. RTKLIB
ver. 2.4.2 Manual, RTKLIB: an open source program package for GNSS positioning.
Available at: http://www.rtklib.com/prog/manual_2.4.2.pdf.
18.
Scilab. Available at:
https://www.scilab.org/.
Received 12.07.2020; accepted in revised form 29.10.2020
Scientific
Journal of Silesian University of Technology. Series Transport is licensed
under a Creative Commons Attribution 4.0 International License