Article
citation information:
Kirschenstein, M., Krasuski, K., Goś,
A. Designating
the error of vertical coordinate of aircraft position in the GPS system. Scientific Journal of Silesian University of
Technology. Series Transport. 2020, 108,
85-94. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2020.108.8.
Małgorzata
KIRSCHENSTEIN[1], Kamil KRASUSKI[2], Artur GOŚ3
DESIGNATING
THE ERROR OF VERTICAL COORDINATE OF AIRCRAFT POSITION IN THE GPS SYSTEM
Summary. This article presents the results of research
concerning the determination of an error of the vertical position of an
aircraft during a flight, taking into account, the flight altitude and the
values of the ZTD tropospheric product. In particular, this work focuses on the
impact of an error in designating the ZTD tropospheric product on the correct
determination of a flight altitude. The authors of this work performed a
scientific experiment for research data of two flights made by a Cessna 172
around the aerodrome in Dęblin. This article shows the findings of the tropospheric
ZTD product specified for the single-frequency SPP positioning method and
dual-frequency PPP positioning method. Based on the obtained results, it was
discovered that the error of the ZTD tropospheric delay causes an altitude
error from 0.08 m at the zenith angle equal to 80o even to 0.79 m at
the zenith angle equal to 85o.
Keywords: GPS system, aircraft position, error of
vertical coordinate, flight test
1. INTRODUCTION
The
emergence of GNSS on-board receivers, on the market, has significantly
facilitated the navigation exploitation of the aircraft. The use of GNSS
on-board receivers outside the usual navigation functions provides a lot of
additional information, for example, connected with specifying atmospheric
parameters, that is, the ionospheric and tropospheric delays [5]. Thus, the
ionosphere delay constitutes a dispersion part of the atmosphere, whereas the
troposphere delay is a neutral part of the atmosphere for GNSS signals [7]. The
impact of the ionospheric delay is particularly important in the GNSS
differential measurements since it causes vector scaling between the reference
station and the on-board GNSS receiver [3]. On the other hand, the tropospheric
correction is reflected in determining the aircraft vertical coordinate. An incorrect
determination of the aircraft altitude may consequently lead to an air incident
or accident. It is, therefore, crucial to conduct scientific research with
regard to the determination and monitoring the value of the tropospheric
correction in the GNSS satellite measurements in aviation.
The basic
equipment of an aircraft is a single frequency GNSS receiver. In this case, the
impact of the tropospheric delay is designated using deterministic models [2].
For this reason, the tropospheric delay is added to the geometric distance
between the satellite and the receiver in an observation equation in the Single
Point Positioning (SPP) code method [6], similar to an observation equation in
GNSS phase measurements. In the SPP method, the tropospheric correction is
defined by means of the Slant Troposphere Delay (STD) values. The STD value
comprises SHD (Slant Hydrostatic Delay) parameters and SWD (Slant Wet Delay)
parameters [8]. The SHD and SWD components are calculated as follows:
-
SHD is determined
on the basis of ZHD values (Zenith Hydrostatic Delay) and the mapping function,
-
SWD is determined
on the basis of the ZWD value (Zenith Wet Delay) and the mapping function.
The sum
of the ZHD and ZWD parameters in its final product is defined as ZTD (Zenith
Troposphere Delay [4].
In case
of on-board dual-frequency GNSS receivers, the scheme of designating the
tropospheric correction varies. Namely, the ZHD parameter is still determined
using the deterministic model, whereas, the ZWD parameter is designated in the
stochastic process. To determine the troposphere correction employing the data
from the dual-frequency GNSS receiver, the Precise Point Positioning (PPP)
method is used [10]. Ultimately, the ZTD tropospheric product is defined as a
sum of the ZHD component from the deterministic model and the ZWD component
from the stochastic model.
In this paper, the authors present and describe
research results concerning the determination of an aircraft vertical error
coordinate in the aspect of applying the ZTD tropospheric correction. Furthermore,
the authors designate the ZTD parameter based on the single-frequency SPP code
method centred on GPS data from an on-board receiver. In addition, the authors
of this work also determine the ZTD parameter, using the dual-frequency PPP
method based on GPS data derived from an on-board receiver. The difference in
the ZTD parameter calculated in the SPP and PPP method allows designating the
aircraft vertical coordinate. The calculations are based on real GPS data
derived from the on-board GNSS receiver mounted in the Cessna 172. The
registered GPS data comes from two air tests performed on the same day (16
June) around the aerodrome in Dęblin.
2. RESEARCH METHODOLOGY
The lack of the aircraft vertical coordinate of the aircraft is determined
using the following dependence [1]:
(1)
where:
- error of
vertical coordinate of aircraft (expressed in metres),
- error of Zenith
Troposphere Delay (expressed in metres),
- zenith angle
(expressed in degrees).
The parameter is determined
from a relationship as below:
(2)
where:
- Zenith
Troposphere Delay calculated from single-frequency SPP method (expressed in metres),
- Zenith
Troposphere Delay estimated from dual-frequency PPP method (expressed in metres).
Finally, after a transformation, we
receive:
(3)
Then,
the parameter of the zenith angle 
can be defined as the completion of the elevation of the
angle as shown below:
(4)
where:
- elevation angle
(expressed in degrees).
The
relationship from Equation 3 shows the error impact of designating the ZTD
parameter upon the accuracy of determining a flight altitude for
single-frequency GNSS observations. In Equation 3, the variable parameters are:
- parameter of the tropospheric delay determined in the
SPP code method,
- parameter of the tropospheric delay determined in the
PPP positioning method,
- parameter of the zenith angle z,
-
in the analysed
case, the parameter is determined
from the deterministic model in the SPP code method, whereas the parameter constitutes the
reference value of the ZTD parameter, computed in the PPP measurement
technique.
3. THE RESEARCH EXPERIMENT
In the research experiment, the
authors designated the aircraft vertical coordinate based on the received data
about the ZTD parameter and with regard to the zenith angle. The experimental
test was carried out for GPS data coming from two air tests, executed on the
same day. The first flight test lasted from 11:58:44 to 12:34:57 in accordance
with GPST. The second flight test lasted from 14:31:50 to 15:00:04 in
accordance with GPST. Both air tests were conducted by the Cessna 172, on board
of which the Topcon HiperPro receiver was installed. In the first air test, the
flight altitude of the Cessna 172 reached a maximum of 636 m, whereas in the
second test it amounted to 352 m. The vertical flight trajectory in both flight
tests is presented in the function of a measurement epoch in Figs. 1 and 2. In
the investigations, the value of the ZTD parameter in the SPP code method was
designated in the first place. The calculations of the Cessna 172, using the
code observations for the SPP method, were made in the RTKLIB v.2.4.2 programme
[9]. Furthermore, the ZTD parameter for the SPP code method was determined based
on the troposphere model of Saastamoinen. In this case, the ZTD parameter was
determined using the deterministic model of the tropospheric delay.
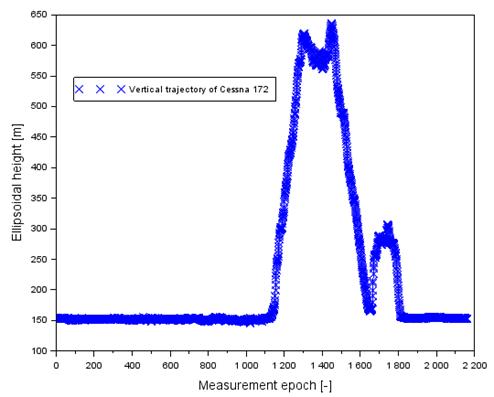
Fig. 1. The vertical profile of Cessna 172 in
flight no. 1
[Source: based on Scilab
software]
In the second one, the authors
designated the ZTD based on the PPP measurement technique. The calculations of
the position of the Cessna 172, using a dual-frequency GPS code and phase
measuring technique in the PPP measurement method was made in the CSRS-PPP
v.2.26.0 programme [11]. Furthermore, the ZTD parameter for the PPP measurement
technique was determined based on the troposphere VMF model. The ZHD parameter
was determined from the deterministic model, whereas the ZWD parameter from the
stochastic model of developing GPS code-phase observations.
Thereafter, a
comparison of the ZTD value was made in accordance with formula (2) to
determine the tropospheric delay error. Finally, the parameter error of the
vertical aircraft coordinate was determined in accordance with formula (3). It
should be added that the calculation adopted boundary values of the zenith
angle from 80o, to 85o, with, with a leap every 1o.
The numeric calculations were made in the Scilab v.6.0.0 [12].
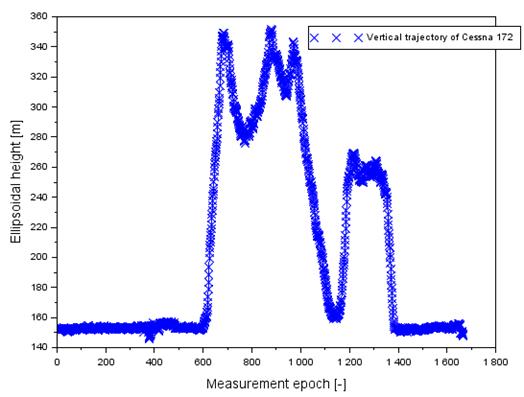
Fig. 2. The vertical profile of Cessna 172 in flight no. 2
[Source: based on Scilab software]
4. RESULTS
The
obtained results are depicted in Figs. 3 to 6. In the first place, the values
of the parameter for flight no 1
were depicted in Fig. 3. The values range from 0.014
to 0.039 m. Furthermore, the average value of the parameter equals 0.020 m.
Fig. 4
shows the results of designating a flight error of the Cessna 172 during flight
no 1. The highest values of the vertical coordinate error are visible for the
zenith angle equal to 85o. Then, the parameter takes the values from
0.155 to 0.443 m. In addition, the average value equals 0.220 m and the median
value is equal to 0.200 m. For the zenith angle of 84o, the altitude
error values range from 0.129 to 0.369 m. Moreover, the average value is 0.191
m, with the median being equal to 0.167 m. For the zenith angle of 83o,
the altitude error values range from 0.110 to 0.317 m. In addition, the average
value equals 0.164 m, with the median being equal to 0.143 m. For the zenith
angle of 82o, the values of altitude error range from 0.097 to 0.277
m. While the average value is 0.144 m, with the median being equal to 0.126 m.
For the zenith angle of 81o, the altitude error values are between
0.086 m and 0.247 m. Furthermore, the average value is 0.128 m, with the median
being equal to 0.112 m. For the zenith angle of 80o, the altitude
error values range from 0.078 to 0.222 m. In addition, the average value is
0.115 m with the median being equal to 0.101 m. Having made an objective
assessment of the results in Fig. 4, it is worth stressing that the maximum
values are noticeable when the parameter also takes the highest values. On the
other hand, when the flight altitude increases, the parameter rises as well.
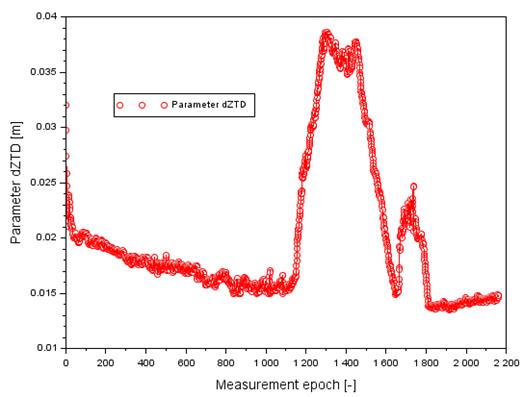
Fig.
3. The values of dZTD term in flight no. 1
[Source:
based on Scilab software]
In the
second place, the values of the parameter for flight no. 2
were depicted in Fig. 5. The values range from 0.051
to 0.068 m. Furthermore, the average value of the parameter equals 0.060 m.
Fig. 6
shows the results of designating a flight error of the Cessna 172 during flight
no 2. The highest error values of the aircraft vertical coordinate are visible
for the zenith angle equal to 85o, as well as for flight no. 1. Then,
the parameter value ranges from
0.583 to 0.781 m. In addition, the average value is 0.685 m with
the median being equal to 0.661 m. When the zenith angle equals 84o,
the altitude error values range from 0.486
to 0.651 m. Moreover, the average value is 0.571 m with
the median being equal to 0.551 m. Then, the zenith angle is equal to 83o.
The altitude error values are between 0.417
and 0.558 m. Furthermore, the average value equals 0.490 m,
with the median being equal to 0.473 m.
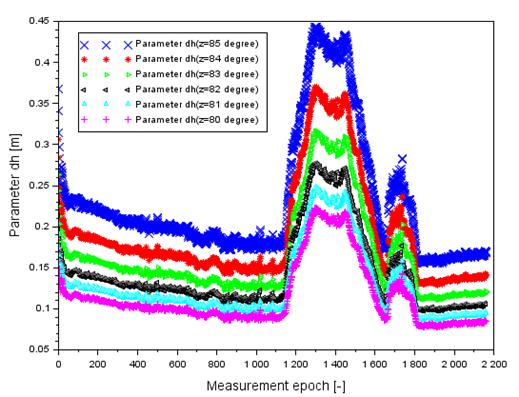
Fig. 4. The values of dh parameter in flight no. 1
[Source: based on Scilab software]
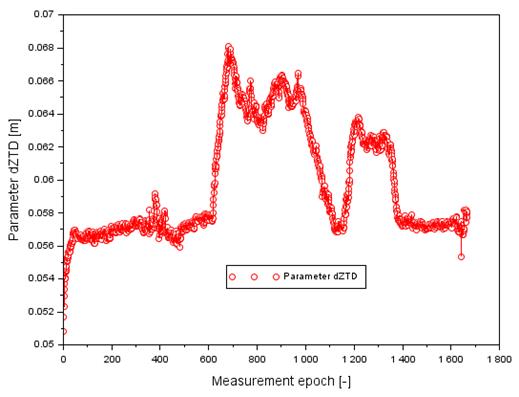
Fig. 5. The values of dZTD term in flight no. 2
[Source: based on Scilab software]
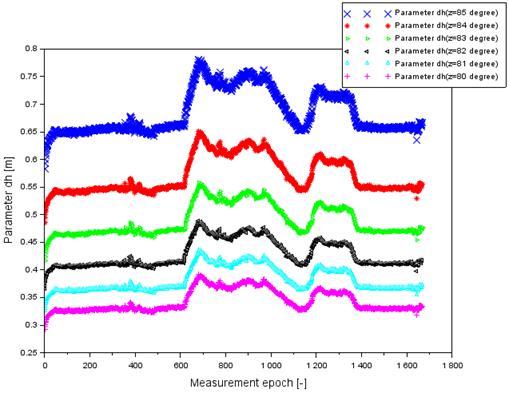
Fig. 6. The values of dh parameter in flight no. 2
[Source: based on Scilab software]
Then, for the zenith
of 82o, the altitude error values range from 0.365
to 0.489 m. In addition, the average value is equal to 0.429
m, with the median being equal to 0.414 m. Moreover, for the zenith angle equal
to 81o, the altitude error values are between 0.325
and 0.435 m. Moreover, the average value is 0.382 m, with
the median being equal to 0.368 m. For the zenith angle of 80o, the
altitude error values range from 0.293
to 0.391 m. In addition, the average value is equal to 0.343
m, with the median being equal to 0.332 m. Similar to flight no 1, the values 
are maximum. Also,
the parameter has got the
highest value. On the other hand, when the vertical coordinate increases, the
parameter also rises. Based
on the results obtained from the flight nos. 1 and 2, it is clear that the
impact of the product of tropospheric ZTD is quite significant when determining
the component of the vertical position of the aircraft.
5. CONCLUSION
This article presents research
findings describing the vertical coordinate error of an aircraft during the
execution of experimental flights. This work shows the algorithm of designating
the vertical component error of the aircraft position in the function of the
ZTD troposphere product error as well as the zenith angle. The scientific
experiment was supported by the conducted investigations, in which the research
material from two air tests was used. The flights were executed by the Cessna
172 over the aerodrome in Dęblin. This article determines the ZTD
tropospheric product on the basis of the deterministic model for the SPP code
method. Moreover, the ZTD reference value was defined for the SPP
dual-frequency measurement technology. The difference in parameter ZTD has
allowed estimating the impact of the tropospheric delay on the designation of
real aircraft altitude. Based on the obtained results of the investigations, it
was discovered that
- in test no 1, the error of designating the altitude
coordinate of the aircraft equals between 0.078 m for the zenith angle of 80o
to 0.443 m for the zenith angle of 85o,
- in test no 2, the error of designating the altitude
coordinate of the aircraft equals between 0.293 m for the zenith angle of 80o
to 0.781 m for the zenith angle of 85o,
- an increase in the error parameter of the ZTD product
results in an error increase of designating the altitude coordinate.
The test
results can be used in practice for the application of the GPS navigation
system in air transport. Moreover, the algorithm presented in this article can
also be implemented in the GLONASS system in aviation. The presented work may
have a significant impact on research related to the monitoring of the
troposphere in air operations and in aircraft navigation.
Acknowledgements
This paper was supported by the Military
University of Aviation in
the year 2020.
References
1.
Beutler G., I. Bauersima, W. Gurtner, M. Rothacher,
T. Schildknechtt, A. Geinger. 1987. Atmospheric
refraction and other important biases in GPS carrier phase observations, in
atmospheric effects on geodetic space measurements.
Monograph 12. Kensington, Australia. P. 15-43.
2.
Bosy J. 2005. „Precise processing of satellite
GPS observations in local networks located in mountain areas”. Zeszyty Naukowe Akademii Rolniczej we
Wrocławiu 522. ISSN: 0867-7964.
3.
Figurski M. 2001. Określenie wybranych parametrów atmosfery na podstawie
permanentnych obserwacji GPS i ich wpływ na dokładność
opracowań pomiarów satelitarnych. [In Polish: Determination of selected atmosphere parameters
based on permanent GPS observations and their impact on the accuracy of
satellite measurements]. ISBN: 83-88442-29-2. Warsaw: WAT.
4.
Kleijer F. 2004. „Troposphere modeling and
filtering for precise GPS leveling”.
PhD thesis. Department of Mathematical Geodesy and Positioning, Delft
University of Technology. Netherlands.
5.
Kutsenko
O., S. Ilnytska, V. Konin. 2018. „Investigation of the the residual
tropospheric error influence on the coordinate determination accuracy in a
satellite landing system”. Aviation
22(4): 156-165.
6.
Sanz Subirana J., Juan Zornoza J. M.,
Hernández-Pajares M. 2013. GNSS Data Processing. Vol. I: Fundamentals
and Algorithms. Publisher: ESA Communications, ESTEC, Noordwijk,
Netherlands. ISBN: 978-92-9221-886-7, ESA TM-23/1.
7.
Schaer S. 1999. „Mapping and predicting the Earth’s ionosphere using Global
Positioning System”. PhD
thesis. Neunundfünfzigster Band. Vol. 59. Zürich, Switzerland.
8.
Schüler T. 2001. “On ground-based GPS tropospheric delay
estimation”. PhD thesis.
Institute of Geodesy and Navigation, University FAF, Munich Germany.
9.
Takasu T. 2013. RTKLIB ver. 2.4.2 Manual, RTKLIB: an open source
program package for GNSS positioning. Available at:
http://www.rtklib.com/prog/manual_2.4.2.pdf.
10.
Zhao Q., Y. Yao, W. Yao, Z. Li. 2018. “Real-time precise point
positioning-based zenith tropospheric delay for precipitation forecasting”.
Scientific Reports 8(7939).
DOI: 10.1038/s41598-018-26299-3.
11.
Precise Point Positioning. Available at:
https://webapp.geod.nrcan.gc.ca/geod/tools-outils/ppp.php.
12.
Scilab. Available at: https://www.scilab.org/.
Received 11.02.2020; accepted in revised form 24.05.2020
Scientific
Journal of Silesian University of Technology. Series Transport is licensed
under a Creative Commons Attribution 4.0 International License