Article
citation information:
Matyja, T. Tilt test of a pallet load unit
– simulation studies. Scientific
Journal of Silesian University of Technology. Series Transport. 2020, 107, 107-117. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2020.107.8.
Tomasz MATYJA[1]
TILT
TEST OF A PALLET LOAD UNIT – SIMULATION STUDIES
Summary. This paper presents a dynamic model of a palletised
load unit during a static tilt test. The stability (also called rigidity) of a
load unit was evaluated. The palletised load unit was built of packages forming
layers and protected against disintegration by stretch film. The aim of this
study was to compare the results of a static tilt test with a commonly used and
recommended dynamic acceleration test.
Keywords: tilt test, load unit, stability, simulation
model
1. INTRODUCTION
In road transport, loads that are carried will
be affected by inertia forces of considerable value. It is assumed that during
sudden braking, usually resulting from a dangerous road situation, the vehicle
and the load may be subject to retardation of the range 1g [3, 6-9]. Inertial forces may cause the load to shift in the
cargo space, resulting in permanent deformation and even damage [13]. For
loading units made of many smaller packages, the unit may disintegrate. A sharp
change in the centre of gravity position of the load poses a great threat to
the vehicle and driver. A significant part of road accidents is caused directly
or indirectly by improper load fastening or inadequate securing. To protect
against the disintegration of a load unit formed on a pallet from smaller
packages, the stretch film is commonly used. It is the cheapest and easiest
method to use to ensure unit stability (rigidity) [1, 2, 11].
Directive 2014/47/EU [8] and EUMOS 40509 [9]
recommend checking the stability of a load unit by means of dynamic tests,
which may consist of appropriate rapid acceleration of the load (acceleration
tests) or its stopping (crash tests). In both cases, access to specialised
devices in the form of mobile platforms is required. Therefore, dynamic testing
is expensive.
When there is no access to such devices, the
stability of the load unit can also be assessed by performing a static test on
an inclined plane [10]. It is for this purpose that a rigid plate with
dimensions enabling the pallet to be placed on it and a forklift to raise the
end of the plate (Fig. 1). Tilt tests have another application; testing
the stress relaxation and creep of the film stretch in time (endurance tests).
This type of testing is not a subject of interest in this work.
This paper presents a simplified model of a
pallet load unit with a layered structure during a quasi-static tilt test.
Cargo layers shifts were limited by pre-stretched stretch film. The tilt test
simulation results were compared with the simulation results of a typical
dynamic test performed in accordance with standards [5, 12]. The developed
mathematical model of the tilt test was implemented in the Matlab environment.
Fig. 1. Performing a static test using a
forklift
2. TILT TEST SIMULATION MODEL
During dynamic tests, the
acceleration acting on the load unit should reach the value of 0.8g [5, 12]. This value of acceleration acting
down the ramp can be obtained with a slope 53.13o. Of course, this
is accompanied by a decrease in the force pressing the load unit perpendicular
to the inclined plane. Therefore, it is difficult to directly compare the
effectiveness of both dynamic and static tests. It seems expedient to consider
the acceleration ratio 
, which is the quotient of the
acceleration components parallel and perpendicular to the pallet plane. For the
maximum acceleration value will be:
|
|
|
(1) |
Equation 1 shows that to achieve
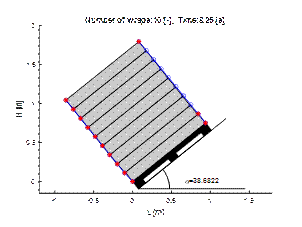
comparable conditions to the dynamic test, a tilt of the ramp at an angle 38.66o is necessary. When
the lifting speed of the forklift is constant V=const, the height of the lift H(t)=Vt
and based on the drawing (Fig.3), the angle of inclination of the ramp
changes according to the relationship:
|
|
|
(2) |
At a typical value of forklift speed
V=0.2m/s and plate length D=2m,
the time needed to achieve the suitable angle of inclination is equal t=6.25s. Differences in acceleration ratio during dynamic and static
tests are explained in Fig. 2.
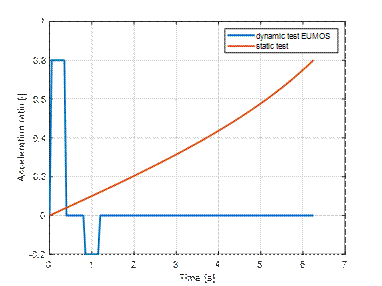
Fig. 2. The time
course of the acceleration ratio in dynamic and static tests
It can be assumed that the lifting
process is slow enough to neglect the inertia forces associated with rotation
in the cargo movement equations. This is confirmed by the considerations
presented below. By differentiating twice formula for the sine of the angle a, we get:
|
|
|
(3) |
And after transformations finally:
|
|
|
(4) |
When a changes from 0o to 60o then the angular velocity changes from V/D to 2V/D. At the same time, the angular acceleration varies from 0 to 
. In addition to gravitational
acceleration, the cargo will also be affected by inertial accelerations:
centrifugal, tangential and Corilois acceleration. The maximum acceleration
values in the anticipated platform rotation range will be, respectively:
|
|
|
(5) |
At a low lifting speed 
, relative speed 
and dimensions 
, these accelerations will be
respectively: 
and are much smaller than the
parallel component to the platform 
, which at the maximum tilt of the
platform is equal 
.
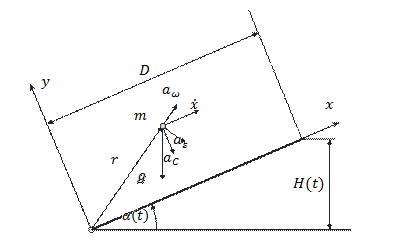
Fig. 3. Acceleration
acting on the load when the platform is lifting
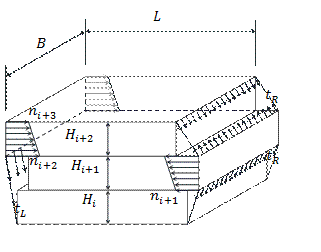
The equation of motion of a selected
layer of cargo, in a direction parallel to the ramp, in a non-inertial
coordinate system, after neglecting the accelerations caused by rotation, has
the form (Fig. 4):
|
|
|
(6) |
where: Fi, Fi+1 – friction forces on the upper and lower
surface of the layer,
Ri – resultant force of
the stretch film reaction.
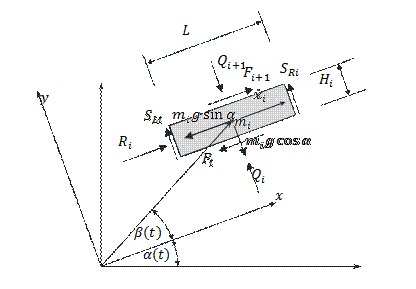
Fig. 4. Forces acting on the
selected layer of load
The friction model adopted in the
task includes the stick-slip phenomenon, Coulomb friction, the Stribeck effect
and viscous friction. Friction force is a function of:
|
|
|
(7) |
where: 
speed of layer 
relative to the layer below,
– is the velocity of the load
layers breaking,
– speed threshold of the Stribeck
phenomenon,
– Coulomb speed threshold,
– static and kinetic friction
coefficients,
– viscous friction coefficient.
Friction forces depend on the value
of pressure forces between the layers, which can be determined from the
formula:
|
|
|
(8) |
where: SLi,
SRi – action forces
of the packaging with stretch film.
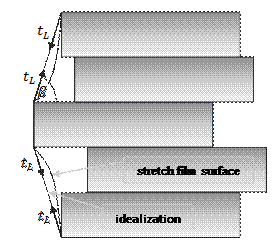
Restoring force Ri= Ri(x1,…,xN)
works on the most shifted layers of cargo and is results of the containment
force (tension force obtained initially it the wrapping process) and increase
of this force due to additional stretching of the film in a direction parallel
to the pallet (Fig. 5). A simplified linear model of stretch film deformation
was assumed, which is spanned on the most put forward vertices of the load
layers. An additional effect of stretching the film in a direction
perpendicular to the surface of the pallet are tensions whose resultants are
the forces SLi= SLi(x1,…,xN)
and SRi= SRi(x1,…,xN)
operated on the side edges of the
layer.
The model assumes that the layers of
cargo can only slide on each other and will not rotate. Therefore, the
simulation should be stopped when the stability of the stack of cargo layers
cannot be maintained. This occurs when the resultant of forces acting on the
layer in direction perpendicular to the pallet goes beyond the zone of contact
with the layer below. The developed software automatically detects this case.
Stability of the stack must be checked starting from the top layer down.
3. RESULTS OF SIMULATION TESTS
Stability test of a load unit made
of 9 identical layers of packages was simulated, each with a mass 50kg and height 0.15m. The coefficient of kinetic friction between the layers was 0.3
and between the bottom layer and the palette 0.8. The static friction
coefficient was 20% higher than the kinetic.
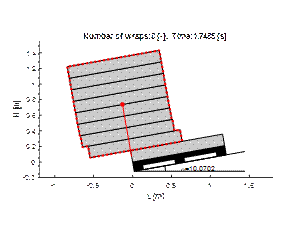
In the beginning, simulations of the
load unit tilt test without stretch film were carried out. With a relatively
small angle of inclination, the layers of the load shifted so much that the
stack lost its stability (Fig. 6). The first layer remained stationary due to
the much higher coefficient of friction between it and the pallet.
|
|
|
Fig. 5. Assumed
tension distribution in the stretch film and stretch film surface idealisation
|
|
|
Fig. 6. Stack of
packaging without stretch film wrapping
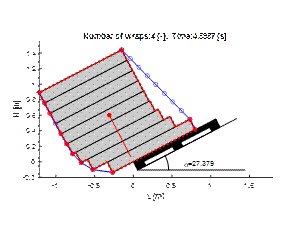
Then, the load was wrapped with four
layers of stretch film, which corresponded to a containment force of 51N.
The results of the tilt test simulation are shown in Fig. 6. The four layers of
film do not protect the packaging against sliding relative to each other and
relative to the pallet, but to some extent keep them in a group. For this
reason also, the first layer begins to slide off the palette. The simulation
was interrupted when the packaging stack lost stability.
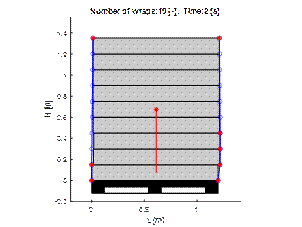
Next, the cargo wrapped with ten
layers of film was simulated (containment force equal 127.5 N). This
amount of wrapping seems sufficient to maintain the stability of the loading
unit. This was based on a dynamic test. Figs. 8 to 12 enable comparison of the
results of simulations of both static and dynamic tests. In the case of dynamic
test simulation, the factor migsina in the equations of motion (6) must
be replaced by mia(t),
where a(t) acceleration changes over
time according to [8]. The formula (8) for determining pressure forces should
also be modified.
|
|
|
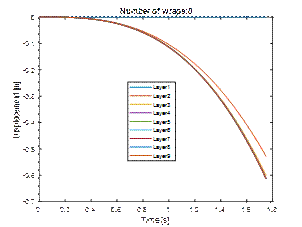
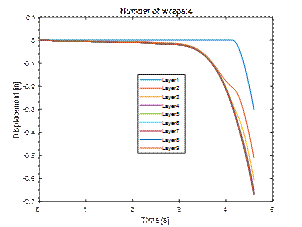
Fig. 7. Displacement
of the layers (cargo wrapped four times with stretch film)
|
|
|
Fig. 8. Cargo layers
displacement (left: tilt test; right: acceleration test)
|
|
|
Fig. 9. Cargo layers
displacement velocities
|
|
|
Fig. 10. Visualisation
of the cargo layers displacement (at the end of the simulation)
|
|
|
Fig. 11. Graph of the
total kinetic energy of cargo
|
|
|
Fig. 12. Total
mobility of cargo layers
|
|
|
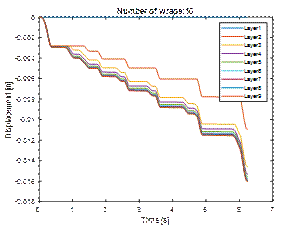
Fig. 13. Cargo layers
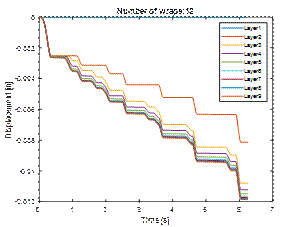
displacement (twelve layers of stretch film)
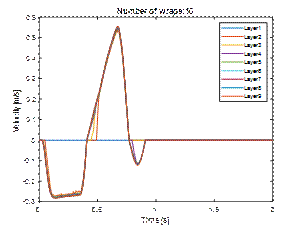
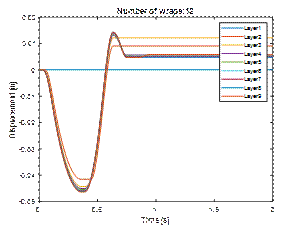
During the dynamic test, the layers
of cargo moved first to the left by about 8 cm and then under the influence of the restoring force to the
right, remaining shifted by about 20
mm. However, during the tilt test, the load systematically moved to the
left, sliding down the pallet in stages. Finally, the displacement was about 16
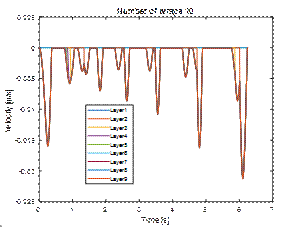
mm (Fig. 8 and 10). From the analysis of the speed diagram (Fig. 9), it can be
seen that slips and sticks occurred at that time. In both cases, the first
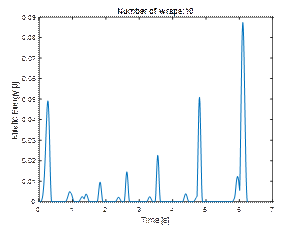
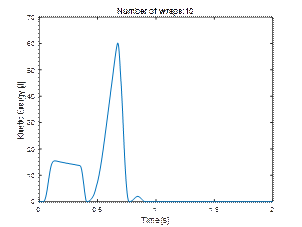
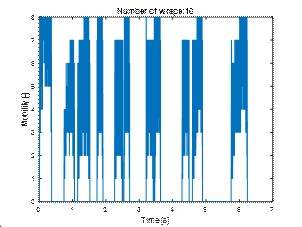
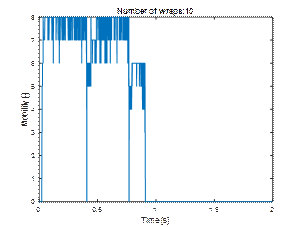
layer remained stationary. The graphs of total kinetic energy (Fig. 11) and
layer mobility differ significantly as well (Fig. 12).
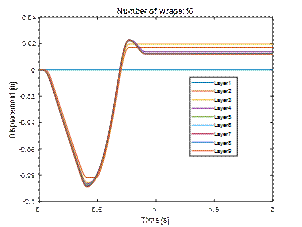
Simulations, when the cargo is
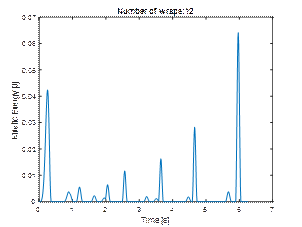
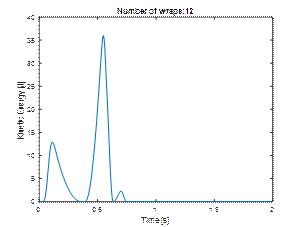
secured with twelve layers of stretch film, were also carried out. The results
in the form of displacements and kinetic energy are shown in the charts (Figs.
13 and 14). It can be observed that increasing the number of wraps by two
increases the stability of the cargo more than 20%. Other simulation studies have shown that the relationship
between load stability and the number of stretch film layers is not linear.
Initially, a rapid improvement in stability with each successive layer of film
is observed. Then this increase is getting smaller. There is a certain limit
value of the number of stretch film layers, which its further increase no
longer adds improvement. Optimal use of film has an impact on costs and the
environment.
|
|
|
Fig. 14. Total kinetic
energy of cargo (twelve layers of stretch film)
As the simulation shows, static and
dynamic tests are completely different. However, practical conclusions from
both tests are comparable. In the analysed case, ten layers of stretch film are
able to sufficiently secure the load on the pallet against disintegration.
4. CONCLUSIONS
Based on the simulation tests
carried out, it can be stated that the dynamic test cannot be replaced by a
static test. The detailed results obtained, in the form of displacement values,
packaging speed and other tested parameters are radically different in both
tests. On the other hand, the effect of tests in the form of determining the
minimum number of stretch film wraps is comparable. The static test is also
cheap and very easy to perform. Therefore, it can be used when there are no
other options, and as a pre-test before performing a dynamic test to reduce its
costs.
References
1.
ASTM D4649. Standard
Guide for Selection and Use of Stretch Wrap Films.
2.
Bisha J. 2012. „Correlation of the elastic properties of stretch film
in unit load containment”. PhD
thesis. Blacksburg, USA: Virginia Tech.
3.
Cieśla Maria,
Tadeusz Opasiak. 2014. Load securing in cargo transport units. Katowice:
PAN. ISBN 978-83-940763-2-0.
4.
Directive
2014/47/EU of the European Parliament and of the Council. The technical roadside
inspection of the roadworthiness of commercial vehicles circulating in the
Union.
5.
EUMOS 40509-2012. Test
method for load unit rigidity.
6.
Gąska Damian,
Tomasz Haniszewski. 2016. “Modelling studies on the use of aluminium
alloys in lightweight load-carrying crane structures”. Transport Problems 11(3): 13-20. DOI:
10.20858/tp.2016.11.3.2. ISSN: 1896-0596.
7.
Haniszewski
Tomasz, Damian Gaska. 2017. “Numerical modelling of I-Beam jib crane with
local stresses in wheel supporting flanges - influence of hoisting
speed”. Nase More 64(1): 7-13.
DOI: 10.17818/NM/2017/1.2. ISSN: 0469-6255.
8.
Haniszewski
Tomasz. 2017. „Modeling the dynamics of cargo lifting process by
overhead crane for dynamic overload factor estimation”. Journal of
Vibroengineering 19(1): 75-86. DOI:
10.21595/jve.2016.17310. ISSN: 1392-8716.
9.
Kuskil’din
R.B., M.A. Vasilyeva. 2017. „Dynamic loads during safety braking of the container
with cargo”. Procedia Engineering 206: 248-253. DOI: https://doi.org/10.1016/j.proeng.2017.10.469.
10.
Singh J., K. Saha,
T. Sewell. 2017. „Evaluation of stability of unit loads for tilt and
shock events during distribution”. Journal of Applied Packaging
Research 9(3):73-93.
11.
Tepić J., V.
Todić, I. Tanackov, D. Lukić, G. Stojić, S. Sremac. 2012.
“Modular system design for plastic euro pallets”. Metalurgija: 51(2): 241-244. ISSN:
0543-5846.
12.
The Transportable
Test Pallet. Available at: https://www.bestpackaging.com.au/.
13.
Vlkovský M.,
M. Šmerek, J. Michálek. 2017. „Cargo securing during transport depending on the type of a road”. IOP Conf. Series: Materials Science
and Engineering 245 042001. DOI: 10.1088/1757-899X/245/4/042001.
Received 16.02.2020; accepted in revised form 29.04.2020
Scientific
Journal of Silesian University of Technology. Series Transport is licensed
under a Creative Commons Attribution 4.0 International License