Article
citation information:
Škrabala,
J., Hajdučík, A., Medvecký, Š., Brumerčík,
F. Optimalisation of the blade movement of the mower. Scientific Journal of Silesian University of
Technology. Series Transport. 2019, 105,
213-222. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2019.105.17.
Jozef ŠKRABALA[1],
Adrián HAJDUČÍK[2],
Štefan MEDVECKÝ[3],
František BRUMERČÍK[4]
OPTIMALISATION
OF THE BLADE MOVEMENT OF THE MOWER
Summary. This article presents the correct adjustment of the
mower’s blade movement relative to the forward movement of the mower.
Everywhere around us are gardens, parks and meadow, which gives us reason to
solve issues with mowing. The first part of this article shows agricultural
machines, which are used today and the principle of correct cut of grass
stalks. The next part shows the method of adjusting the mower’s blade
speed. Design of a simple model was done with the use of Solid Edge Premium
CAD. For computation, MSC Adams was used and post-processing was done with the
use of Matlab. The connection between MSC Adams and Matlab was created by
co-simulation.
Keywords: mower’s blade,
mowing, movement, kinematics
1. INTRODUCTION
Everywhere around us are grassy
places, which give us the idea to design special mountain mower with respect to
the quality of cut. This mower is intended to mow private gardens, city parks,
grass fields and hardly accessible areas. Nowadays, there are so many types of
mowers, which are intended for various areas of mowing. Nevertheless, users
will not avoid using their combination. Furthermore, the right type of mowing
machine has to be chosen for a given area. The main reason mountain mower can
replace multiple machines is that the construction is adapted for unfavourable
conditions, and uses autonomous control, which increases access for limited
terrain. Also, this mower is designed for the highest possible quality of cut,
with which the blade’s design is directly related. To achieve these
assumptions, it is necessary to determine the correct blade’s teeth
geometry [12, 13, 16]. Thereafter, it is necessary to determine the speed of
the blade relative to the mower’s movement for proper and healthy cutting
[3-6].
2. MOWER MACHINES
Generally, mower
machines are special agricultural machines for mowing plants. Mowers developed
with the evolution of humanity. Gradually, mowers evolved from hand scythes,
through a horse-drawn mower to today's types. Today, there are many types of
mower designed to mow different lands. The most common types are:
·
hand
mower:
§
scythe,
§
sickle,
§
manual
mower,
·
petrol
and electric mower:
§
rotary
mower,
§
drum
mower,
§
string
trimmer,
§
brush
cutter,
·
tractor
mower.
To better understand the
problem, two groups of mowers have been created with respect to the type of
mowing:
·
rotary
mower:
§
horizontal,
§
vertical,
·
reciprocating
bar mower:
§
cutting
without support,
§
cutting
with support.
2.1. Rotary mower
Typical mower of this
group is the gasoline rotary mower, which is shown in Fig. 1. Their great
advantage is the possibility to attach a basket that could also harvest the
leaves. The cutting height is usually adjustable from 3.5 to 5 cm. The right
choice of rotary mower depends on the frequency of mowing, size of the area and
demands of the operator. For example, depending on the size of the mowed area,
the right blade size has to be chosen (blade size 32 cm –up to 200 m2,
40 cm – up to 350 m2, 45cm – up to 500 m2,
53cm – up to 1000 m2 and longer – over 1000 m2).
There are many types of blades, but the quality of the cut is mainly influenced
by their sharpening. The cut of the stalk by a rotary mower is characterised as
a cut without support [11, 17].
Fig. 1. Rotary mower [15]
2.2. Reciprocating bar mower
The reciprocating bar mower is marked with sickle bars. This type of
mower is a very special type of agricultural machine, which is shown in Fig. 2.
Sickle bar mowers are divided into two groups:
·
sickle
bar with support (Fig. 3a),
·
sickle
bar without support (Fig. 3b).
Fig. 2. Sickle bar mower [15]
The cut without support
is characterised by a very high blade speed, which often exceeds 30 m.s-1.
This type of cut is executed by stalk tearing, which adversely affects the
health of the plant. Schematic illustration of the blade without support is
shown in Fig. 3a), where position 1 stands for the blade.
On the contrary, the cut
with support has little demands on the speed of the blades. The cut occurs
already at the velocity of 2 m.s-1 and it could be compared to stalk
shearing. Fig. 3b shows the blade (position 1) and the support (position 2) [1,
2].
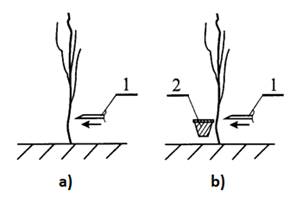
Fig. 3. Types of cutting: a) without support b) with support
3. SOLUTION OF
KINEMATICS OF MOWER BLADES
The solution of the kinematics of mower blades is done via the kinematic
analysis of blades movement relative to the forward movement of sickle bar
mower [18]. In this case, there is a double stroke bar considered – a
reciprocating movement of both bars [12].
3.1. Modelling mower and
its parts
A simple model was
created in CAD software [7, 10], which is shown in Fig. 4. The simplifications
will not affect the results, because they are not related to machine
kinematics. They also have a positive impact on the complexity of the
mathematical model and thus accelerate the computational time.
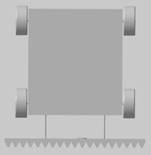
Fig. 4. Simplified model of the mower
The next step was to
import the CAD model into the MSC.Adams software, where all parts have been
modelled (Fig. 5).
By defining the
relations between the parts, we used the fixed joint, translational joint and
revolute joint connections. Additionally, we used two types of motions:
rotational and translational motion and a driving motor [8, 9].
Fixed joint is used on
the ground because it has zero degrees of freedom (DOF). Revolute joint is
created between two parts and it is related to one axis. This connection is
used to define the wheels and rotational parts of the crank mechanism.
Translational joint is created between two parts with defined direction. This
joint is used between the ground and the vehicle body and also between the body
and the bars [19].
The contact is defined
between the wheels and the ground. Also used is the Coulomb friction model
to prevent the wheels from slipping.
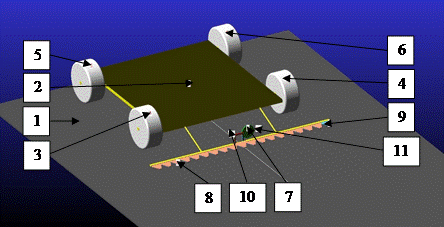
Fig. 5. Parts of the mower:
1 – ground; 2 - body of the vehicle; 3 - right
front wheel; 4 - left front wheel;
5 - rear right wheel; 6
- rear left wheel; 7 - drive rail; 8 - upper bar; 9 - bottom bar;
10 - top handlebar; 11 -
lower handlebar
3.2. The principle of
mower tracking
To illustrate the paths
of each blade (the top and bottom bars), it is necessary to create the points
(markers), which will be monitored. These points will be used for kinematic
analysis in MATLAB [14, 15]. Fig. 6 illustrates individual markers on the top
sickle bar (points A to G). The markers were created also on the second bar –
Fig. 7.
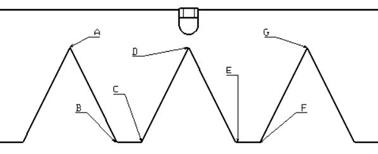
Fig. 6. Markers of the top sickle bar (A – G)
3.3. Mathematical model
First step of the
solution was to make a simple mathematical model of the solved problem. The
reciprocating movement of the blades is solved as a simple crank mechanism
(Fig. 8).
For
the solution of this mechanism, the vector method is used. It is one loop
multi-element case, where the rotational movement is transformed into the
translational movement. The computation of basic parameters of the crank
mechanism follows according to Fig. 9.
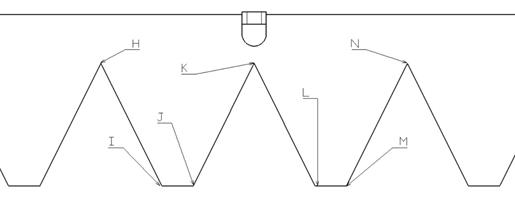
Fig. 7. Markers of the lower sickle bar (H – N)
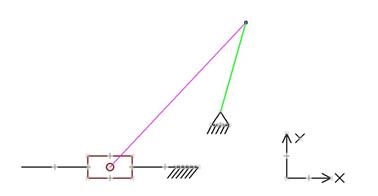
Fig. 8. Schematic drawing of a crank mechanism
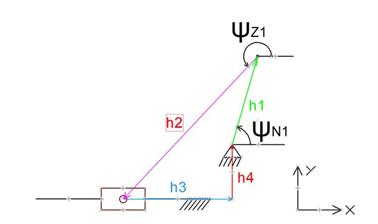
Fig. 9. Block scheme for computation of the crank mechanism
The number of kinematic loops can
be calculated as:
. (1)
The kinematic loops equations are
defined as:
. (2)
x
axis: 
, (3)
y
axis:. 
(4)
3.4. Co-simulation and
data processing
MATLAB Simulink is used
for co-simulation with MSC Adams, because there are more opportunities to
analyse the received data. First step was to choose input and output signals,
which will be exported to MATLAB. As the input signals, the velocity of the
mower and the angular velocity of the crank mechanism were determined. The
paths of all markers were the output signals. After exporting procedure, a
Simulink program was generated. This program was represented by a simple
block diagram, which is shown in Fig. 10.
Fig. 10. Simulink generated scheme
Subsequently, the scheme
was copied into the new program, where the inputs (velocity of the mower and
angular velocity of crank mechanism) are set. The outputs were the observed
point’s positions and the control speed of the crank mechanism. After the
calculation procedure, all data were exported to the Simulink workspace, where
they were stored as vectors.
After running the
simulation, all data were started to process and analyse the issue of the lawn
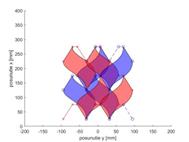
mowing quality. The starting point’s vectors are created to display the
geometry of the bars on the graph – top bar with red colour and the lower
bar with blue colour (Fig. 11). According to the definition of the slider
vectors of the individual points, the paths of the knife blades acting on the
given movements are plotted on the graph. After the paths of the individual
points rendering, the passed areas were coloured. There could be seen in places
of the bends of the stalk, the places of the cutting of the stalk and the
places with the uncut grass blades remained.
4. RESULTS AND
DISCUSSION
Depending on the setting
of the crank mechanism, speeds relative to the forward motion of the mower can
occur in these three situations after analysis [18]:
·
right
cut of the plants (Fig. 11a),
·
bending
of the plants (Fig. 11b),
·
skipping
of the uncut plants (Fig. 11c).
The last type of mowing
is the worst. There are usually unmowed places because the trajectory of
blade’s shapes does not cover the entire mowed area. This case occurs
when the angular velocity of the crank mechanism is low relative to the mower
motion.
When the stalks are
bent, that is a case of high crank speed. This state is energetically
unfavourable. This requires passing the same trajectory more times by mowing.
|
|
|
|
|
a) |
b) |
c) |
Fig. 11. Blade movement:a) Right mowing; b) Bending of stalks; c)
Unmowed places
When the right cut
occurs, the energetic demands are optimal and the stalks damages are minimal. Optimal
speeds based on the performed analysis are shown in Tab. 1.
Tab. 1
Optimal angular velocity of
crank mechanism relative to mower movement
|
Mower speed (m.s-1) |
Crank speed (min-1) |
|
1 |
850 |
|
1,5 |
1100 |
|
2 |
1350 |
The kinematic analysis
in MSC Adams demonstrates the possibilities of solving complex tasks of mutual
motion. The results of the solution were verified on the second prototype of
mountain mower (MM2). All performed tests were successful.
Acknowledgement
The research is supported by the Cultural and Educational Grant Agency of
the Ministry of Education, Science, Research and Sport of the Slovak Republic
under project No. 046ŽU-4/2018.
References
1.
Caban J., P. Drozdziel, J. Vrábel, B. Šarkan, A.
Marczuk, L. Krzywonos, I. Rybicka. 2016.
„The research on ageing of glycol-based brake fluids of vehicles in
operation”. Advances in Science and
Technology 10(32): 9-16.
2.
Caban
J., A. Marczuk, B. Šarkan, J. Vrábel. 2015. „Studies on
operational wear of glycol-based brake fluid”. Przemysł Chemiczny 94(10): 1802-1806.
3.
Czech Piotr. 2012. „Determination of the course
of pressure in an internal combustion engine cylinder with the use of vibration
effects and radial basis function - preliminary research”. Communications
in Computer and Information Science 329: 175-182. DOI https://doi.org/10.1007/978-3-642-34050-5_21.
Springer, Berlin, Heidelberg. ISBN:978-3-642-34049-9. ISSN: 1865-0929. In:
Mikulski Jerzy (eds), Telematics in the transport environment, 12th
International Conference on Transport Systems Telematics, Katowice Ustron,
Poland, October 10-13, 2012.
4.
Czech Piotr. 2011. „Diagnosing of disturbances
in the ignition system by vibroacoustic signals and radial basis function -
preliminary research”. Communications in Computer and Information Science
239: 110-117. DOI https://doi.org/10.1007/978-3-642-24660-9_13. Springer,
Berlin, Heidelberg. ISBN:978-3-642-24659-3. ISSN: 1865-0929. In: Mikulski
Jerzy (eds), Modern transport telematics, 11th International Conference on
Transport Systems Telematics, Katowice Ustron, Poland, October 19-22, 2011.
5.
Faturík
Lukáš, Libor Trško, Slavomír Hrček, Otakar
Bokuvka. 2014. „Comparison of structural design in high and ultra-high cycle
fatigue regions”. Transactions of
FAMENA 38(4): 1-12. ISSN 1333-1124.
6.
Figlus
Tomasz, Mateusz Koziol. 2016. „Diagnosis of
early-stage damage to polymer - glass fibre composites using non-contact
measurement of vibration signals”. Journal of Mechanical Science and Technology 30(8): 3567-3576. ISSN 1738-494X. DOI: 10.1007/s12206-016-0717-1.
7.
Gąska Damian, Tomasz Haniszewski. 2016.
“Modelling studies on the use of aluminium alloys in lightweight
load-carrying crane structures”. Transport
Problems 11(3): 13-20. DOI: 10.20858/tp.2016.11.3.2. ISSN: 1896-0596.
8.
Glowacz Adam, Zygfryd Glowacz. 2017. „Diagnosis
of the three-phase induction motor using thermal imaging”. Infrared physics & technology 81:
7-16. ISSN 1350-4495. DOI: 10.1016/j.infrared.2016.12.003.
9.
Glowacz Adam, Zygfryd Glowacz. 2017.
„Diagnosis of stator faults of the single-phase induction motor using
acoustic signals”. Applied acoustic
117A: 20-27. ISSN 0003-682X. DOI: DOI: 10.1016/j.apacoust.2016.10.012.
10. Haniszewski Tomasz,
Damian Gaska. 2017. “Numerical modelling of I-Beam jib crane with local
stresses in wheel supporting flanges - influence of hoisting speed”. Nase More 64(1): 7-13. DOI:
10.17818/NM/2017/1.2. ISSN: 0469-6255.
11. Kai-Sheng Wang, Chen-Kang
Huang. 2018. “Intelligent Robotic Lawn Mower
Design”. International Conference
on System Science and Engineering (ICSSE). DOI: 10.1109/ICSSE.2018.8520053.
12. Kohár Róbert, Slavomír
Hrček. 2014. „Dynamic Analysis of a Rolling Bearing Cage with
Respect to the Elastic Properties of the Cage for the Axial and Radial Load
Cases”. Communications –
Scientific Letters of the University of Zilina 16(3A): 74-81. ISSN
1335-4205.
13. Koziol Mateusz, Tomasz Figlus. 2017.
„Evaluation of the Failure Progress in the Static Bending of GFRP
Laminates Reinforced With a Classic Plain-Woven Fabric and a 3D Fabric, by
Means of the Vibrations Analysis”. Polymer
composites 38(6): 1070-1085.
14. Rudecki M., O. Kildisheva.
2013. „A modified sickle bar mower: increased flexibility for harvesting
native plant seeds”. Native Plants
Journal 14(3): 257-260. DOI: 10.3368/npj.14.3.257.
15. Siregar Ikhsan, Anggi Ridho, Dinda Gustia, Agung
Triono, Yulia Shafira. 2018. “Product design of a lawn mower tool for
agriculture”. Conference Series
Materials Science and Engineering 420(1): 1-11. DOI:
10.1088/1757-899X/420/1/012140.
16. Skrúcaný
Tomáš, Branislav Šarkan, Tomasz Figlus, et al. 2017. „Measuring of noise
emitted by moving vehicles”.
MATEC Web of Conferences 107: 00072. ISBN: 978-1-5108-4114-7. DOI: https://doi.org/10.1051/matecconf/201710700072.
17. Škrabala Jozef. 2018. „Design
of the remote controlled mower“. Diploma thesis, Bratislava: Slovak
University of Technology in Bratislava.
18. Škrabala Jozef,
Adrián Hajdučík, Štefan Medvecký. 2019.
“Optimization of mower blades movement considering to mower ́s
motion”. Novus Scientia. Proceedings
of XVI. International Scientific Conference of PhD students of engineering
faculties of technical universities and universities. Košice: Technical
University of Košice. ISBN 978-80-553-3249-9.
19.
Thomas
D.G. 1992. Fundamentals of Vehicle
Dynamics. Society of Automotive Engineers. 495 p. ISBN 1560911999.
Received 07.09.2019; accepted in revised form 26.11.2019
Scientific
Journal of Silesian University of Technology. Series Transport is licensed
under a Creative Commons Attribution 4.0 International License