Article
citation information:
Malakova, S. Kinematic properties and
meshing condition of elliptical gear train. Scientific
Journal of Silesian University of Technology. Series Transport. 2019, 104, 95-105. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2019.104.9.
Silvia MALÁKOVÁ[1]
KINEMATIC PROPERTIES AND MESHING CONDITION OF
ELLIPTICAL GEAR TRAIN
Summary. This paper presents
the concept of eccentric elliptical gear train able to generate a variable gear
ratio law. The first step in the noncircular gears virtual design process is
the generation of the conjugate pitch curves, starting from a predesigned law
of motion for the driven element or a predesigned geometry for the driving gear
pitch curve. By designing a pair of non-circular gears, which are able to
perform a proper gear ratio function, the output member of a mechanism can be
effectively forced to move according to a prescribed law of motion, when
operated at a constant input-velocity. This mechanism is designed to obtain a
specific motion law. Detailed knowledge of meshing conditions is a prerequisite
for studying kinematic conditions in gearings, as well as the strength
calculation of gearing.
Keywords: non-circle
gear, elliptical gear, kinematic conditions, meshing conditions.
1. INTRODUCTION
The idea of non-circular gears
originates from the precursors of the engineering thought. These gears were
sketched by Leonardo da Vinci, and found their application in many types of
mechanical devices, like locks and toys. In the late 19th century, Franz
Reuleaux ordered at Gustav Voigt Mechanische Werkstatt in Berlin, a series of
non-circular gear models to help study kinematics. The gears made at those
times had simplified tooth shapes and, for this reason, the meshing conditions
were not always correct [1].
Several mechanical devices can be
designed to obtain a prescribed motion law of output element. When a mechanical
system is used to obtain a required motion of the output link, non-circular
gears are another possible choice. In spite of their poor diffusion, the
non-circular gears can be in a variety of mechanical systems. In fact, since
the gear ratio function they generate is variable, a purely mechanical control
can be performed on the input/output relationship. For this reason, non-circular
gears are useful in those mechanisms whose task is to force an output element
to move according to a specific law of motion. Automatic equipment in printing
presses, textile industry, packaging machines and quick-return mechanisms
represent the most diffuse applications.
A common challenge in the design of
mechanical systems is the kinematic synthesis of a mechanism in order to
satisfy a set of motion characteristics [2, 3]. Frequent requirements are to
guide a rigid body through a series of specified positions and orientations
(rigid body guidance), to force a coupler point to move along a prescribed
trajectory (path generation), or to cause an output member to move according to
a specific function of the input motion (function generation) [4].
The application of non-circular gears in function generating mechanisms has been
proposed and discussed in [5, 6]. By designing a pair of non-circular
gears, which are able to perform a proper gear ratio function, the output
member of a mechanism can be effectively forced to move according to
a prescribed law of motion, when operated at constant input velocity [7].
In typical arrangements, a pair of variable radius pitch curves are synthesized
to drive a slider-crank mechanism according to prescribed motion law. For many
applications, non-circular gears provide some benefits over cams, although they
are more difficult to design and expensive to manufacture. The main advantages
are the lower weight-to-strength ratios and the absence of gross separation or
decoupling of moving parts [8].
The
gearing with changing transmission gear ratio is used in the practice, even
though the "standard" gearing with constant transmission gear ratio
is used more often. This article examines the mesh conditions proposed in
elliptical gears, as I speed and power ratios in this proposed gearings. The
work is devoted to the analysis of these kinematic conditions in the proposed
gearings and examines their differences from "standard" ring gear
transmission with a constant transference number. The problem is solved for
elliptical, eccentric gear with a continuously variable gear ratio.
2. DESIGNED NON-CIRCULAR GEARING
Generation of this
noncircular gear was developed starting from the hypothesis such as the law of
driven gear motion, variation of gear transmission ratio and design of driving
gear pitch curve [9, 10]. This model of non-circular gear was designed for
variable gear ratio to a range from 0.5 through 1 to 2. This transfer should be
formed by two identical wheels with the number of teeth z1 = z2
= 24 and gearing module mn = 3.75 mm, the axial distance
a = 90 mm and for a one direction of rotation.
Given that each gear
must satisfy the conditions of proper meshing, it was necessary to determine
the geometric shape of the wheels. The pitch curve corresponded to the pitch
circles in regular gears. They represent a non-circular gear as two rollers
rolling together without slip, provided there is no addendum modification and
the nominal axle distance is used.
The gearing is designed
such that the pitch curve is composed of an ellipse formed with the basic
parameters shown in Figure 1. A geometric centre of the gear is not the centre
of wheel’s rotation. The centre of gear’s rotation is in the focus
point of the ellipse.
The pitch ellipse has a
large half-axis x = 45 mm, which is half of the axial distance. The second
half-axis is determined by the distance from the focus point 45 mm (Fig.1),
whose position is determined by considering the desired gear ratio.
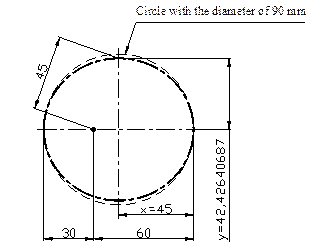
Fig. 1. Pitch ellipse for designed gearing
In
pursuit of the kinematical conditions of the proposed gearings with
eccentrically selected centres of rotation, we start from one of the conditions of a correct mesh,
which states that the circumferential velocities in the pitch point are equal
and their projections into the profile normal line are the same.
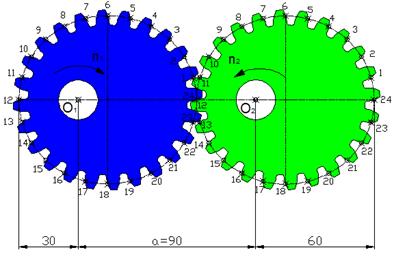
Fig. 2. Designed eccentric elliptical gear train
The conventional gearing involute starts from the base
circle, in which case, it is the base of the evolute of the ellipse. The
evolute for the left and right side teeth is not the same. Each of the twelve
teeth is different; the next twelve teeth of the same wheel are the same. The
side curve is the involute, and is different for the active and passive side of
the tooth; the teeth are asymmetrical. The gears for a given variable
transmission have been proposed as elliptical - eccentrically placed, so that
conditions were right shot. The geometric model of the proposed gear is shown
in Figure 2. Teeth of gearing are numbered; the picture depicts the mesh of the
tooth No. 24 and No. 12.
3. MESHING CONDITION OF DESIGNED ELLIPTICAL GEARING
Detailed knowledge of
the meshing conditions is a prerequisite not only for solution of the
deformation of the gearing but also for the research of speed, power and energy
conditions and for the strength calculation of gearing [11-13]. The
characteristic points of meshing in the frontal plane of the spur gear are
shown in Figure 3.
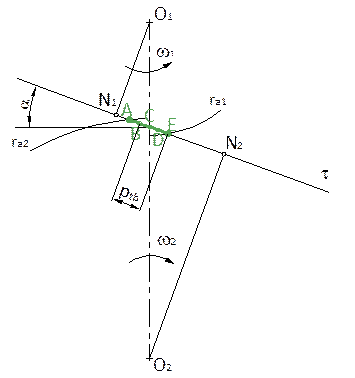
Fig. 3. Characteristic points of meshing
For the sense of
rotation shown in Figure 3, the energy is transmitted from the gear pinion 1 to
the gear wheel 2 (the gear 1 is the drive and the gear 2 is driven) and the
meshing proceeds from point A to point E. Points A, E are the outer or end
points of the pressure line AE. The sections AB and DE are sections of two-pair
of meshing teeth, that is, when two pairs of teeth meshing the gears are in
contact. When there is meshing point in these sections, so this pair of teeth
is always considered with the meshing of the adjacent pair of teeth in the
second section. The line section BD is a single-pair section, that is, there is
only one pair of mating teeth on this section of the pressure line.
Involute gear is characterised
by rectilinear pressure line [14]. This is true even for the designed
elliptical gearing. The result of the examination for teeth 24 - 12 in meshing
is shown in Figure 4.
Fig. 4. Face of pressure line for designed gear train
The characteristic points A, E are the end
points of the meshing line AE, which is component of pressure line τ, in
the meshing line is realise meshing of teeth of gearing.
The length of meshing line for spur gears is
calculated by equation:
![]() (1)
(1)
where ra1,2
is radius of addendum circle, rb1,2 is radius of base circle, a is
axial distance and α is pressure angle.
The expression of meshing
properties is used coefficient of meshing εα, calculate by
equation:
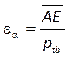 (2)
(2)
where ptb is base pitch.
The value of the coefficient of meshing for spur gears with straight teeth is
in the range 1<εα <2.
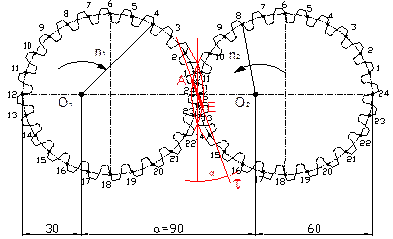
Fig. 5. The meshing line AE for teeth 24 - 12 in meshing
The length of meshing lineaof
designed eccentrically elliptical gearing cannot calculate by equation for the
circular involute gearing. Therefore, they are intended of graphic for each
pair of teeth of meshing (for example, Figure 5 and Figure 6).
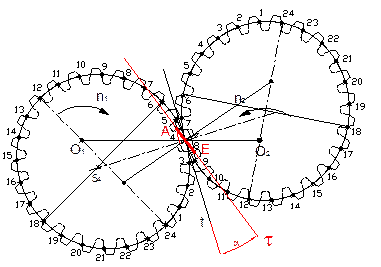
Fig. 6. The meshing line AE for teeth 4 - 8 in meshing
The
measured value of length of meshing line AE and calculated value of meshing coefficient εα for
designer elliptical and spur gearing are shown in Table 1.
Tab.
1
Coefficient
of meshing εα and length of the meshing line AE
|
Elliptical gearing |
Spur gearing (mn=3,75mm) |
||||||
|
Meshing teeth input - output |
AE (mm) |
εα |
r1-i (mm) |
r2-j (mm) |
Transmission ratio ui=r2/r1 |
AE (mm) |
εα |
|
24 - 12 |
14.406 |
1.222 |
60 |
30 |
0.5 |
17.527 |
1.488 |
|
01 - 11 |
14.412 |
1.223 |
59.458 |
30.541 |
0.5136 |
17.542 |
1.489 |
|
02 - 10 |
14.436 |
1.225 |
57.891 |
32.108 |
0.5546 |
17.583 |
1.492 |
|
03 - 9 |
14.503 |
1.231 |
55.449 |
34.550 |
0.6230 |
17.636 |
1.497 |
|
04 - 8 |
14.52 |
1.232 |
52.338 |
37.663 |
0.7196 |
17.686 |
1.501 |
|
05 - 7 |
14.548 |
1.235 |
48.779 |
41.221 |
0.8450 |
17.721 |
1.504 |
|
26 - 6 |
14.594 |
1.239 |
45 |
45 |
1 |
18.235 |
1.647 |
There is greatest value
of length meshing line AE for a one pair of teeth in designed non-circular
gearing, which in meshing have a gear ratio equal value 1.0. The designed
eccentric elliptical gearing has different profiles for all teeth, the gearing
is comprised of teeth with different profiles. The coefficient of meshing
εα and the length of the meshing line AE for each pair of
teeth in meshing are not constant for this designed gear train. These values
are constant for standard circular spur gear.
Necessary detailed
knowledge of meshing condition is mandatory for solution deformation and
stiffness of gearing as well as for the strength calculation of gearing. There
is a rectilinear pressure (meshing) line for involute gear. For a standard
circular involute gearing the length of meshing line is the same for all teeth
pairs in the meshing. For designed elliptical gearing with variable gear ratio,
the length of the meshing line and coefficient of meshing for each pair of
teeth in meshing are not constant.
4. KINEMATIC CONDITION OF DESIGNED ELLIPTICAL GEARING
Kinematic conditions of
designed elliptical gear train were processed for gear No. 1 (with the rotation
centre at point O1) and gear No. 2 (with the rotation centre at
point O2). The kinematic dependences for both designed gear wheels
are shown in one graph together. There are teeth of the first gear wheel on the
horizontal axis.
There is a continuously changing
gear ratio for designed non-circular gear train in Figure 7, during one
rotation of the drive gear wheel. Thus, the gear ratio changes over the time of
one rotation of the drive gear wheel, from u=0.5 through u=1.0 until u=2.0 and
back. If the value of gear ratio less than 1.0, this is an overdrive. The gear
ratio value greater than 1.0 signifies a speed reduction.
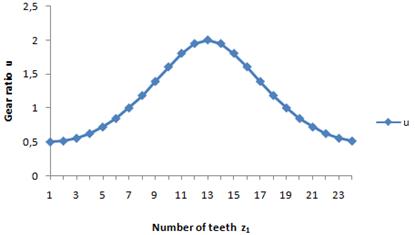
Fig. 7. Gear ratio of designed non-circular gear train
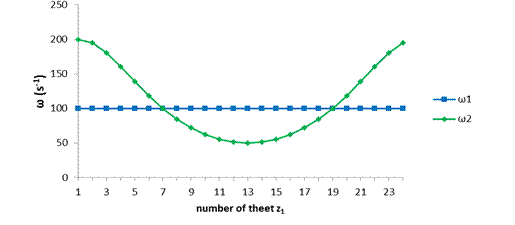
Fig. 8. Rotational speed of designed non-circular gear
train
The standard spur gears
have a constantly rotational speed on the drive wheel gear and on the driven
wheel gear. This non-circular gearing with variable gear ratio has a not
constant of rotational speed for the driven gear wheel. Figure 8 shows the
change of the rotation speed on the driven gear wheel (ω2) at a
constant rotation speed for the drive gear wheel, for value ω1
= 100 s-1.
The movement of spur
gear is defined in the face plane, therefore, kinematics of this motion is
planar [16]. The points of gear are moved along a circular path at a
circumferential velocity at the image central point C determined by equation:
![]() (3)
(3)
where r1,2 is radius of
pitch circle, ω1,2 is a rotational speed.
Figure 9 shows the speed
ratios for the meshing of the teeth No. 4 (drive wheel) and teeth No. 8 (driven
wheel) at the central point.
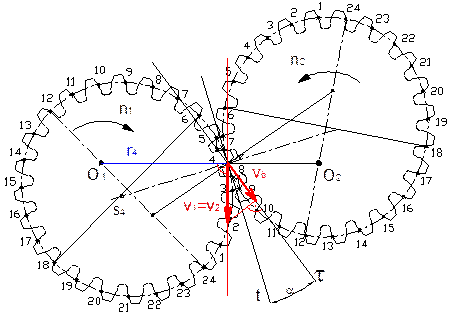
Fig. 9. Circumferential velocity for teeth 4 - 8 in meshing
in the central point
In the case of the
designed elliptical gearing, the size of the circumferential force in the
central point of the shot is different for each pair in the meshing. The
direction of the circumferential velocities of the individual pairs of meshing
teeth is the same (Fig. 10).
The graph of
circumferential velocity in the central points for the pairs of teeth in meshing
is presented in Figure 11.
The circumferential
velocity for designed non-circular gearing is not constant but changes
continuously, depending on the number of gear ratio.
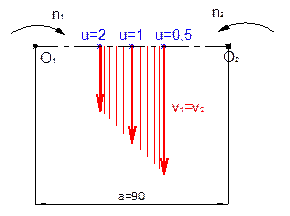
Fig. 10. Changing the size and position
of the circumferential velocity at the central points of the pairs of
teeth (u - is gear ratio)
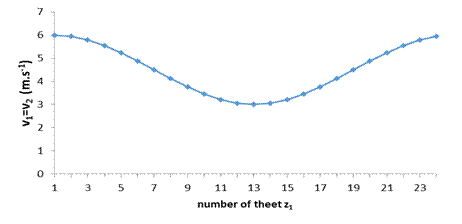
Fig. 11. Circumferential velocity in the central point
5. CONCLUSION
The
examined eccentric elliptical gear train with continuously varying gear ratio
is based on the requirements, for particular gear transmission parameters.
These are gears with asymmetric tooth profile. Properties of this gearing are
different from the properties of standard circular gears – spur gear. The
gear ratio of this elliptical gear train is not constant but fluidly varies
from 0.5 to 2.0 and back. In this way, the gear ratio changes during one
revolution of the driven gear. For a standard circular involute gearing, the
length of meshing line is the same for all teeth pairs in the meshing. For
designed elliptical gearing with variable gear ratio, the length of the meshing
line and coefficient of meshing for each pair of teeth in meshing are not the
same. There, the size of the circumferential velocity in the central point for
the pairs of the teeth is different for each pair in the meshing. The direction
of the circumferential velocities of the individual pairs of meshing teeth is
the same, the position of these circumferential velocities change with respect
to the centres of rotation.
This
paper was written within the framework of Grant project VEGA 1/0290/18
and APVV-16-0259.
References
1.
Zarebski Igor, Tadeusz Sałacinski.
2007. „Designing and WEDM manufacturing of
non-circular gears.“ In: Advances
in production engineering. APE'2007.
Warsaw.
2.
Litvin
Faydor L., Ignacio Gonzalez-Perezb, Alfonso Fuentesb, Kenichi Hayasakac.
2008. „Design and investigation of gear drives with non-circular gears
applied for speed variation and generation of functions”. Computer Methods in Applied Mechanics and
Engineering 197: 3783-3802. DOI: https://doi.org/10.1016/j.cma.2008.03.001.
3.
Žuľová Lucia, Robert Grega, Jozef
Krajňák, Gabriel Fedorko, Vieroslav Molnár. 2017.
„Optimization of noisiness of mechanical system by using a pneumatic
tuner during a failure of piston machine”. Engineering Failure Analysis 79: 845-851. ISSN 1350-6307.
4.
Tong Shih-Hsi, Yang Daniel C.H. 1998. „Generation of
identical noncircular pitch curves”. Journal
of Mechanical Design 120: 337-341.
5.
Litvin Faydor L., Fuentes Alfonso. 2004. Gear geometry and applied theory. Second edition. Cambridge
University Press, New York. ISBN-100-521-81517-7.
6.
Dooner David. 2001. „Function
generation utilizing an eight-link mechanism and optimized non-circular gear
elements with application to automotive steering“. Proceedings of the Institution of Mechanical Engineers, Part C: Journal
of Mechanical Engineering Science 215(7): 847-857.
7.
Doege Eckart, John Meinen, Tobias Neumaier. 2001. „Numerical
design of a new forging press drive incorporating non-circular gears”. Journal of Engineering Manufacture 215:
467-471.
8.
Dooner David, Seiger Ali. 1995. The kinematic geometry of gearing: a concurrent engineering approach.
Wiley Series in Design Engineering. ISBN-13:
978-0471045977.
9.
Krajňák Jozef, Jaroslav Homišin, Robert Grega,
Matej Urbanský. 2016. „The analysis of the impact of vibrations on
noisiness of the mechanical system”. Diagnostyka
17(3): 21-26. ISSN 1641-6414.
10.
Kapelevich Alexander. 2000. „Geometry and design of involute
spur gears with asymmetric teeth”. Mechanism
and Machine Theory 35(1): 117-130.
11.
Bošanský Miroslav, Miroslav Vereš. 2012. Neštandardné ozubené
prevody. [In Slovak: Non-standard
gears]. STU, Bratislava. 159 p. ISBN 978-80-227-3717-5.
12.
Medvecká-Beňová Silvia. 2015. „Properties
of eccentric elliptical gearing”. Pomiary
Automatyka Robotyka 20(2): 17-20. ISSN: 1427-9126. DOI:
10.14313/PAR_220/17.
13.
Urbanský Matej, Jaroslav Homišin, Peter
Kaššay, Jozef Krajňák. 2018. „Measurement of air
springs volume using indirect method in the design of selected pneumatic
devices”. Acta Mechanica et
Automatica 12(1): 19-22. ISSN 1898-4088.
14.
Liu Youyu. 2015. „Study of optimal strategy and
linkage-model for external non-circular helical gears shaping”. Proceedings of the Institution of Mechanical
Engineers, Part C: Journal of Mechanical Engineering Science 229(3):
493-504.
Received 11.05.2019; accepted in revised form 17.08.2019
![]()
Scientific
Journal of Silesian University of Technology. Series Transport is licensed
under a Creative Commons Attribution 4.0 International License