Article
citation information:
Kolesnikova, T., Mischenko, N.,
Sakno, O., Suprun, V., Filipova, G.A., Nikitchenko, I. Gorpyniuk, A.,
Nazarenko, M. Theoretical research response time of the mechanism for compression
ratio changing of the conrod-free engine. Scientific
Journal of Silesian University of Technology. Series Transport. 2019, 104, 69-83. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2019.104.7.
Tatiana KOLESNIKOVA[1],
Nikolay MISCHENKO[2], Olha SAKNO[3],
Volodymyr SUPRUN[4],
Galyna A. FILIPOVA[5], Igor NIKITCHENKO[6],
Andrii GORPYNIUK[7],
Mykola NAZARENKO[8]
THEORETICAL RESEARCH RESPONSE TIME OF
THE MECHANISM FOR COMPRESSION RATIO CHANGING OF THE CONROD-FREE
ENGINE
Summary. The mathematical model for calculating the response time of the compression
ratio of the mechanism for compression ratio changing (MCRC) is presented in
this article. This revealed the influence of various engine factors with the
connecting rod and crank mechanism (CRCM) on the operation of the MCRC (for
example, the rate of the compression ratio change). The results of the study of the operation of the MCRC
indicate a strong influence of the values d (relative area of flow passage of channels) and р (pressure) on the response time τ
in the field of their small values. This indicates that with insignificant
changes of the area of
flow passage of channel of the hydraulic lock and the minute oil pressure in the
cavities, a significant response rate of the MCRC is ensured. The results
demonstrate the possibility of speedy compression ratio change in the engine
with the MCRC.
Calculation studies showed that the mechanism full operation occurs quickly (0.02 s per unit εx), which indicates the
expediency of using such a high-pressure pump in a four-stroke gasoline engine
with CRCM. The mechanism movable body complete movement (S = 4 mm) at the oil temperature in the
hydraulic system of 45°C and pressure on
the body of p = 60 bar are stated to occur for 0.2 s.
Keywords: mechanism for compression ratio
changing, connecting rod and crank mechanism, conrod-free engine, response
time, pressure, oil temperature.
1. INTRODUCTION
Substantial progress in fuel
efficiency improvement and exhaust gas toxic components reduction in automobile
engines have become topical issues in recent times [1-3]. Increased state
control over environmental cleanliness and the economic use of nonrenewable
natural resources favoured it [4-6]. Key automotive companies participate in
the state standards development and compete for consumers; they have to improve
their engines and use up-to-date design and technology solutions [7-11].
Innovations are implemented in
up-to-date engines [12,13]. They focus improvements in the engine systems and
mechanisms and transmission units. Fuel equipment elements that improve
operating procedures play a special role in the engine design perfection. In this case, the piston motion law is push-type and depends only on the
connecting rod and crank mechanism (CRCM) constant parameters [14-16]. This circumstance does not allow
the use of compression ratio regulation being a powerful reserve to optimise
engine operating parameters in its running regimes range [17-19].
The compression ratio is believed
to be the internal combustion engine (ICE) constant design parameter as, for
example, the cylinder diameter is. The compression ratio quantity is definitely
determined by the CRCM dimensions and the cylinder head location relative to
the crankshaft axis in the conventional ICE [20,21].
The ICE power and fuel efficiency
are known to rise with the compression ratio growth due to the indicated
efficiency increase. The ICE performance improvement breaks off when the
compression ratio reaches 13...14 due to increase in the mechanical losses.
Therefore, the compression ratio values are optimal.
The compression ratio value is
built into the engine design and differs from the optimum value. The
compression ratio in gasoline engines is limited by detonation. It is less than
optimal and, as a rule, does not exceed 10.
Numerous calculations and
experimental studies show that the compression ratio regulation can ensure 20%
of fuel economy improvement.
The boost pressure in the gasoline
engine can be increased without detonation when the compression ratio is
reduced, and the power-to-volume ratio is increased with a positive effect
along with it. The fuel economy improved under light-load conditions with the
compression ratio increase [22,23].
The compression ratio maximum value does not exceed ε = 14 in most ICE designs with
variable compression ratio. The frictional losses increase with the further
increase of the engine compression ratio. The indicator efficiency, in this
case, does not compensate these losses, so effective efficiency decreases as a
result.
2. THE CONSTRUCTION OF THE CONROD-FREE ICE
The conrod-free ICE (CFICE) is given realisation of a
change compression ratio more than ε = 14. This is one of the ICE possible
designs. The crank and rocker arm mechanism (CRAM) is used in the engine
instead of the traditional CRCM (Figure 1).
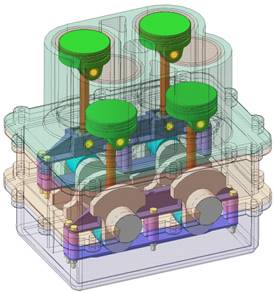
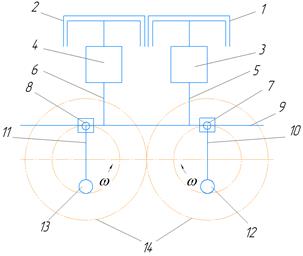
a)
b)
Fig. 1. The graphic presentation of
the conrod-free engine: (a) general view; (b) diagram of the conrod-free engine
with the MCRC; 1, 2 – piston;
3, 4 – MCRC; 5, 6 – piston rod;
7, 8 – crosshead; 9 –
rocker arm; 10, 11 – crankshaft;
12, 13 – crankcase
counterweight; 14 – gear
Experimental design efforts to create conrod-free
engines are carried out in Germany, the USA [24,25], Ukraine [26] and other
countries [9,18,27]. The engine distinctive features are as follows:
·
low friction losses in the entire load range and shaft speed
·
full dynamic balance and stroke uniformity
·
compactness and low specific gravity
The piston strictly rectilinear
motion ensuring absence of lateral loads is the advantage of the CFICE.
The analysis of the CFICE with a
CRAM shows:
·
increase effective efficiency at ε > 14 small mechanical
losses
·
constructively is implemented variable compression
The mechanism for compression ratio
changing (MCRC) was designed in the CFICE. The mechanism has to be studied
theoretically to identify the engine rational parameters.
2.1. The construction of the
mechanism for compression ratio changing
The MCRC is located in the engine
piston.
The MCRC construction diagram is
shown in Figure 2.
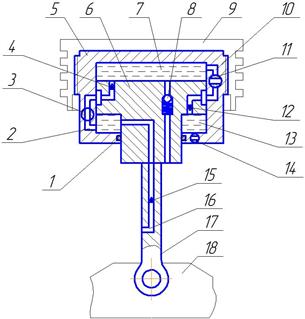
Fig. 2. The
construction diagram of the MCRC: 1 – sealing; 2, 10, 16 – oil
channel;
3, 11, 14 –
hydraulic lock; 4, 12, 15 – check valve; 5 – moving body; 6 –
piston in moving body; 7 – top oil cavity; 13 – bottom oil cavity;
8 – emergency valve; 9 – engine piston;
17 – piston
rod; 18 – rocker arm
Heater was installed on the experimental model of the
engine, which allowed investigating the operation of the mechanism at different
oil temperatures (the oil temperature changed from 20 to 70 degree Celsius).
This allowed us to provide realistic conditions for the MCRC operation.
A valve was installed in the oil supply line to the
mechanism that performed the function of a check valve. The check valve
prevents the creation of loads on the oil pump shaped like overpressure when
the mechanism responds. Experiments were conducted on the mechanism with an
open and closed crane. Oil was fed into the mechanism from the oil pump through
a connecting pipe. The oil pressure in the bottom oil cavity was controlled by
a manometer and maintained at 4.0 atm. In an automobile engine, an oil
lubrication system pump creates such pressure. The turn of the moving body of the mechanism to activate the hydraulic lock was
carried out using an electromagnetic relay. Due to this, the MCRC response time throughout the experiment remained unchanged.
Displacement of the moving body
(Figure 2) occurs under the influence of applied gas forces 
and inertial forces 
, and frictional forces 
between the piston rings and the
cylinder walls and the oil pressure 
.
The
signal from the detonation sensor reaches the MCRC control
mechanism when detonation combustion in the engine cylinder appears. This
causes the turn of the hydraulic locks 3 and 11. The engine piston together with the mechanism moving
body moves down under the force . The
compression ratio decreases until the hydraulic locks return to their original position (position
in Figure 3) and the cycle is repeated.
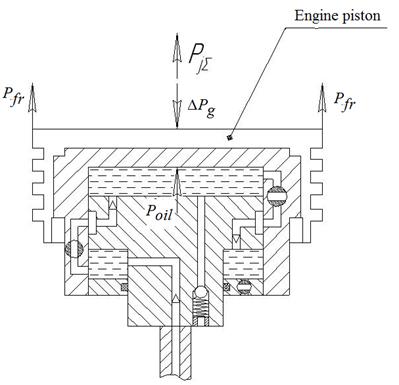
Fig. 3. The scheme
of forces operating
in the MCRC
The compression ratio change occurs
in the engine successive cycles until force closure between the body and the
movable thimble occurs with the help of the hydraulic lock upon the signal from
the detonation sensor.
3. CALCULATION OF THE MCRC RESPONSE TIME
The MCRC response time t is determined according to the
dependence:
(1)
where 
is MCRC
moving body relative movement or, as a consequence, the engine combustion
chamber height change [m] and 
is MCRC moving body average
speed [m/s].
The compression ratio current value
is determined by the formula:
(2)
where 
is cylinder
volume [m3] and 
is combustion
volume [m3].
The compression ratio rate change
per second is determined with regard to the Equation (2):
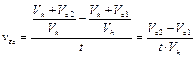(3)
where 
is a
combustion volume 1 [m3] and 
is
combustion volume 2 [m3].
Taking into account the fact that
MCRC moving body relative
movement (Figure 4) is determined by:
(4)
where 
is
an engine piston area [m2].
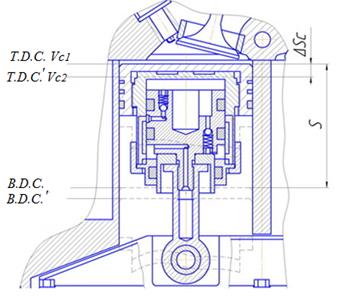
Fig. 4. Engine diagram to determine
the combustion chamber height change:
S
is a piston stroke; is MCRC
moving body relative movement; TDP is top dead point; BDC is bottom dead centre; TDP' is piston position at the top dead
point under the compression ratio change; BDC'
is piston
position at the bottom dead centre under the compression ratio change
The compression ratio rate change is
determined with regard to the Equation (1):
(5)
where S is
piston stroke [m].
The compression ratio rate change per cycle 
is a very important factor for
MCRC. One cycle in a four-stroke engine is known to occur in crankshaft two
revolutions. Therefore, compression ratio rate change is determined:
(6)
where n is
Engine crankshaft speed, min-1
Thus, to obtain the MCRC response
time, it is necessary to determine the moving body movement speed by the
amount . The following MCRC motion equations (Figure 5) have
been worked out to solve this problem:
(7)
where 
is
the mechanism moving body mass, kg; 
is
the mechanism moving body movement, m; 
is
force of gas pressure in the engine cylinder, H; 
is
total inertia force of the mechanism, H; 
is
gravity force of the mechanism, H; 
is
friction force of piston rings, H; 
is
force, which describes hydraulic losses in the mechanism, H; 
is
frictional force in the seals of the mechanism, H.
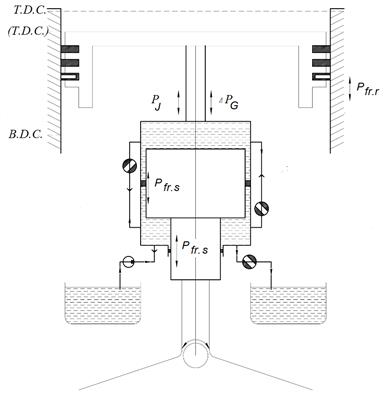
Fig. 5. Scheme for
the MCRC calculation: 
is total
inertia force;
is force of gas pressure; 
is friction
force of piston rings;
is frictional force in the seals of the
mechanism
The mechanism moving body mass is
determined:
(8)
where 
is the engine piston mass, kg; 
is
piston rings
mass, kg; 
is
MCRC moving body mass, kg; 
is
cover mass, kg; 
is
nut mass, kg; 
is
turning bushing mass, kg.
Gas pressure force is determined:
(9)
where 
is
gas pressure in the engine cylinder at an arbitrary time interval, MPa; 
is
atmospheric pressure, MPa.
Total inertial force 
is determined:
(10)
where 
is inertial force from the MCRC
moving masses, H; 
is inertial force from oil in
the MCRC, H.
The inertial force from the MCRC moving masses is
determined:
(11)
The conrod-free engine design
characteristics (the connecting rod coefficient λ, the crank radius R
and the connecting rod length L) are
the following:
(12)
The inertial force from moving
masses of the MCRC is determined:
(13)
where R is crank radius, m; w is the crankshaft angular
velocity, s-1
The inertial force from oil in the MCRC is determined:
(14)
where 
is
oil mass in the mechanism bottom cavity, kg; 
is
oil mass in the mechanism top cavity, kg.
The piston ring set frictional
force is determined:
(15)
where 
is pressure at the end of inlet, MPa; с is the constant coefficient; v is
piston speed, m/s; 
is
reduced temperature, °C (
[28]); 
is
cylinder wall temperature, °C; σ is the
ring radial stress, MPa; 
is
the ring reduced radial stress, MPa (
[29]); 
is
reduced cylinder diameter, mm (
[29]).
The hydraulic losses force 
takes into account the loss of oil flow
through the channels 
, back-pressure valves 
and
hydraulic lock 
that
occur when the oil moves in the mechanism body. The force is formed as:
(16)
where 
is
oil density, kg/m3; 
is
free fall acceleration, m/s2; 
is
the direct or backward channel hydraulic resistance, s2/m5;
is
oil consumption under the direct or backward mechanism body motion, m3/s;
is
active area of piston in moving body, m2
The rubber seals frictional force
under the mechanism moving body motion is determined by the Equation (9):
(17)
where µ is friction
coefficient of the pair of steel-rubber in oil, µ = 0.4 [30]; 
is
pressure in the MCRC top oil cavity, MPa; 
is
pressure in the MCRC bottom oil cavity, MPa; 
& 
is
gasket ring area, m2
Total calculated force is formed as:
(18)
4. THE DESIGN-THEORETICAL RESEARCH RESULTS
The MCRC operation speed was
determined to be affected by the following parameters:
·
pressure on the mechanism on the side of the springing attachment
·
oil temperature
·
channels flow passage area δ
·
the MCRC moving body rotation angle when the hydraulic lock is turned on
·
back pressure in the mechanism bottom oil cavity
The dependence of the MCRC response
time on the relative area of flow passage of channels δ of the hydraulic lock, pressure p and oil temperature t
were obtained experimentally (Figure 6).
The empirical dependence of the response time of the MCRC
is determined:
(19)
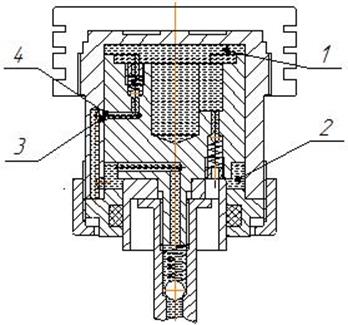
Fig. 6. The MCRC channels scheme for increasing the compression
ratio:
1 – top cavity; 2
– bottom cavity; 3 and 4 – channels
The MCRC response time τ
calculated dependencies on values (d, р, t) were built in Figures 7 and 8.
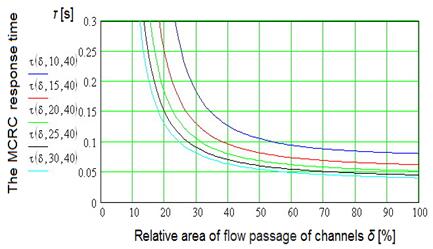
Fig. 7. Dependence of the response time
τ [s] of MCRC on the relative area of
flow passage of channels δ [%]
of the hydraulic lock at different pressures p [MPa]: t = 40°C
The mechanism operating conditions investigation shows that
the MCRC response time τ
decreases under the increasing values (δ, p, t). The
response time τ decreases
sharply over the range from 0 to 40% (value d) and pressure p
over the range 0 to 30 MPa
(Figures 7 and 8). Further increase of values d
and
p has little effect on the response time t. Therefore, when the MCRC
is running in the engine, it is not necessary to turn on the hydraulic lock on
100% when the compression ratio is reduced. This enabled reduction of the MCRC
response time t and the compression
ratio. The hydraulic locks are to be 100% turned on with the compression ratio
increase in order to increase the compression ratio rapidly. Consequently, the
engine operated less under nonoptimal conditions. The compression ratio
increase is the result of the inertia forces action from the body and oil
pressure in the mechanism cavities and the compression ratio change. Therefore,
the mechanism response time t for the compression
ratio rise will be less than that for the value e decrease.
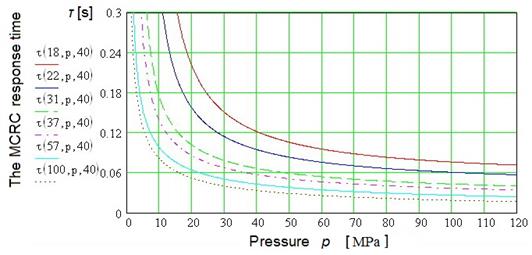
Fig. 8. The MCRC
response time τ [s] dependence on pressures
p [MPa]
in the oil cavity at different relative area of flow passage of channels δ [%] of the hydraulic lock: t = 40°C
Depending on oil temperature t (Figures 9 and 10) has a different character. The curves slope
indicates significant effect of the temperature t in the whole range of its values. The relation between the value t and value t
varies greatly depending on the MCRC operating conditions (values d and р
change). The response time t increases under low
temperatures (0...40°С) and especially at the hydraulic lock small flow passage. Nevertheless, this occurs during engine
warm-up.
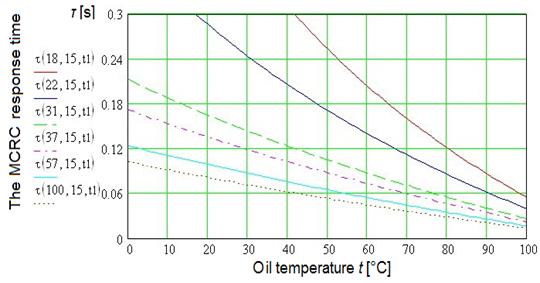
Fig. 9.
Dependence of the
response time τ [s] on oil
temperature t [°C] in the oil cavity 1 (Figure 8) at different relative area of
flow passage of channels δ [%]
of the hydraulic lock: p = 15 MPa
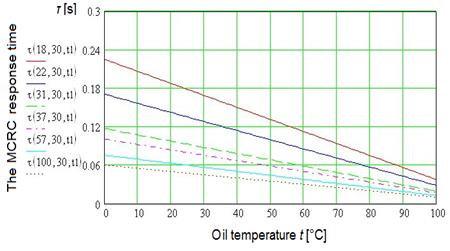
Fig.
10. Dependence of
the response time τ [s] on oil
temperature t [°C] in the oil cavity 1 (Figure 8) at different relative area of
flow passage of channels δ [%]
of the hydraulic lock: p = 30 MPa
The MCRC operation study results indicate strong influence
of the values d and р on
the response time τ in the field
of their small values. This indicates that the MCRC significant response rate
is ensured under insignificant changes in hydraulic lock
flow passage area and little oil pressure in cavities.
Empirical dependence of the oil temperature t (see Figures 9 and 10) on the response
time τ is determined:
(20)
A graphical method was used to determine the Equation (20). The empirical dependence of the
response time of the MCRC is determined by the Equation (19).
The oil pressure in the bottom oil cavity was
controlled by a pressure gauge and maintained at 4 atm. In an ICE, the pressure
can be generated by an oil pump of a lubrication system. The oil temperature
was controlled by an electrical thermometer.
In the experiment, the MCRC response time was tested at
different section of canals and at different viscosity engine oil. Full
operation time is influenced by section of canals, channel form and viscosity
oil. The larger-section channels and the lower the viscosity oil the 0.2 s
of full operation time is enough.
The results demonstrate the possibility of compression
ratio change in the engine with the MCRC.
5. CONCLUSIONS
Theoretical studies were conducted.
These studies were aimed at improving the MCRC for a gasoline four-stroke engine.
The developed mathematical model of
the MCRC calculation revealed the influence of various factors of the engine
with the CRCM on the MCRC operation (for example, the compression ratio rate
change). The experimental data corroborates with the compiled mathematical model
operation.
Calculation studies show that the
mechanism full operation takes place quickly (0.02 s per unit εx), which indicates the
expediency of using such a high-pressure pump in a four-stroke gasoline engine
with CRCM.
The mechanism movable body complete movement (S = 4 mm) at the oil temperature in the hydraulic system
of 45°C
and pressure on the body of p =
60 bar are stated to takes place 0.2 s. The MCRC
response time is average time 0.23 s. An important parameter for the MCRC
response time is the response time until the appearance of detonation
combustion with increasing motor load.
Heat losses in the CFICE are less than in a classical
engine since the piston of the CFICE is shorter than in a classical engine, it
is cut to piston rings.
Currently, the patent application of the MCRC is being
considered in the patent office for the grant of a patent for the invention,
hence, the description of the mechanism is not in full detail.
The mathematical model of the MCRC and the design-theoretical research results can be
used to calculate engines of the same type in order to obtain optimal
parameters for further design or improvement of engines of similar structures.
CFICE can be used as an internal combustion engine for
motor vehicles and other mobile and fixed users as well as a pump or compressor
for creating the working fluid and transport excess pressure (pumping) of
gases, liquids, suspensions, mixtures, suspensions and other agents in various
industries and farms.
Acknowledgements
The authors would like
to express their gratitude to the team of researchers under the leadership of
Dr. Nikolay Mishchenko of the Motor Transport Department of the Automobile Road Institute (Ukraine) for the
design-theoretical research. Also mechanical engineer, Mr. Ruslan Sakno
for the MCRC prototype production, and the referees for their constructive and
valuable suggestions.
References
1.
Mickevicius
T., S. Slavinskas, S. Wierzbicki, K. Duda. 2014. „The effect of
diesel-biodiesel blends on the performance and exhaust emissions of a direct
injection off-road diesel engine”. Transport 29(4): 440-448.
2.
Mikulski M., S. Wierzbicki, M. Smieja, J. Matijosius. 2015. „Effect of CNG in a fuel dose
on the combustion process of a compression-ignition engine”. Transport 30(2): 162-171.
3.
Puškár M., M. Fabian, T. Tomko. 2018.
„Application of multidimensional statistical model for evaluation of
measured data obtained from testing of the HCCI engine prototype”. Diagnostyka 19(1): 19-24. DOI:
http://dx.doi.org/10.29354/diag/78349.
4.
Booto Gaylord Kabongo, Giuseppe Marinelli, Helge
Brattebo¸ Andre Bohne. 2019. “Reducing fuel consumption and
emissions through optimization of the vertical alignment of a road: A case
study of a heavy-duty truck on the Norwegian Highway Route E39”. European Transport/Trasporti Europei 71
(paper 4): 1-33.
5.
Hemisha Makan, Gert J. Heyns. 2018. “Sustainable
supply chain initiatives in reducing greenhouse gas emission within the road
freight industry”. Journal of
Transport and Supply Chain Management 12(a365): 1-10. DOI: https://doi.org/10.4102/jtscm.v12i0.365.
6.
Jacyna M., M. Wasiak, K. Lewczuk, G.
Karoń. 2017. "Noise
and environmental pollution from transport: decisive problems in developing
ecologically efficient transport systems". Journal of Vibroengineering 19: 5639-5655. DOI:
doi.org/10.21595/jve.2017.19371.
7.
Gopal G., L. Suresh Kumar, K.
Vijaya Bahskar Reddy, M. Uma Maheshwara Rao, G. Srinivasulue. 2017. „Analysis of Piston, Connecting rod and Crank
shaft assembly”. Materials Today: Proceedings 4(8): 7810-7819. DOI: https://doi.org/10.1016/j.matpr.2017.07.116.
8.
Islam M.A., K. Heimann, R. J. Browna.
2017. „Microalgae biodiesel: Current status and future needs for engine
performance and emissions”. Renewable and
Sustainable Energy Reviews 79: 1160-1170. DOI: https://doi.org/10.1016/j.rser.2017.05.041.
9.
Rimkevičienė J., V. Ostaševičius, V.
Jūrėnas, R. Gaidys. 2009. „Experiments and simulations of
ultrasonically assisted turning tool”. Mechanika 1: 42-46.
10.
Ubartas M., V. Ostaševičius, S. Samper, V.
Jūrėnas, R. Daukševičius. 2011. „Experimental
investigation of vibrational drilling”. Mechanika 4: 368-373.
11.
Zhang S., C. Zhao, Z. Zhao, D. Yafei, F.
Ma. 2015. „Simulation study of hydraulic differential drive free-piston
engine”. SAE Technical Paper
2015-01-1300. DOI: https://doi.org/10.4271/2015-01-1300.
12.
Czech P.
2012. “Determination of the course of
pressure in an internal combustion engine cylinder with the use of vibration
effects and radial basis function - preliminary research”. TELEMATICS IN
THE TRANSPORT ENVIRONMENT. Edited by: Mikulski J. Book Series: Communications
in Computer and Information Science. Vol.: 329. P. 175-182. Conference: 12th
International Conference on Transport Systems Telematics, Katowice Ustron,
Poland, Oct 10-13, 2012.
13.
Czech P.
2011. “Diagnosing of disturbances in the
ignition system by vibroacoustic signals and radial basis function -
preliminary research”. MODERN TRANSPORT TELEMATICS. Edited by: Mikulski
J. Book Series: Communications in Computer and Information Science. Vol.: 239.
P. 110-117. Conference: 11th International Conference on Transport Systems
Telematics, Katowice Ustron, Poland, Oct 19-22, 2011.
14.
Krajňák
J., J. Homišin, R. Grega, M. Urbanský. 2016. “The analysis of
the impact of vibrations on noisiness of the mechanical system”. Diagnostyka 17(3): 21-26. ISSN
1641-6414.
15.
Sága M., L. Jakubovičová. 2014.
“Computational analysis of contact stress distribution in the case of
mutual stewing of roller bearing rings”. Applied Mechanics and Materials 474: 363-368.
16.
Urbanský M., J. Homišin, P. Kaššay, J.
Krajňák. 2018. “Measurement of air springs volume using
indirect method in the design of selected pneumatic devices”. Acta Mechanica et Automatica 12(1):
19-22. ISSN 1898-4088.
17.
Haag J., F. Kock, M. Chiodi, O. Mack, M.
Bargende, C. Naumann, N. Slavinskaya, A. Heron, U. Riedel, C. Ferrari.
2013. „Development approach for the investigation of homogeneous charge
compression ignition in a free-piston engine”. SAE Technical Paper 2013-24-0047. DOI: https://doi.org/10.4271/2013-24-0047.
18.
Reis V.L., G.B. Daniel,
K.L. Cavalca.
2014. „Dynamic analysis of a lubricated planar slider-crank mechanism
considering friction and Hertz contact effects”. Mechanism and
Machine Theory 74: 257-273. DOI:
https://doi.org/10.1016/j.mechmachtheory.2013.11.009.
19.
Xu Z.P., S.Q. Chang. 2013.
„Simulation of an opposed-piston four-stroke free-piston
generator”. Applied Mechanics and
Materials 336-338: 585-589. DOI:
https://doi.org/10.4028/www.scientific.net/amm.336-338.585.
20.
Yan H.,
D. Wang, Z. Xu. 2015. „Design and simulation of opposed-piston
four-stroke free-piston linear generator”. SAE Technical Paper 2015-01-1277. DOI: https://doi.org/10.4271/2015-01-1277.
21.
Zhu X.,
J. Xu, Y. Liu, B.
Cen, X.
Lu, Z. Zeng.
2017. „Failure analysis of a failed connecting rod cap and connecting
bolts of a reciprocating compressor”. Engineering
Failure Analysis 74: 218-227. DOI: https://doi.org/10.1016/j.engfailanal.2017.01.016.
22.
Kojima S., S. Kiga, K. Moteki, E.
Takahashi, K. Matsuoka. 2018. “Development of a New 2L Gasoline VC-Turbo
Engine with the World’s First Variable Compression Ratio
Technology”. SAE Technical Paper 2018-01-0371. DOI: 10.4271/2018-01-0371.
23.
Zhang S.,
Z. Zhao, C. Zhao, F. Zhang, Y. Liu. 2016. “Design approach and
dimensionless analysis of a differential driving hydraulic free piston
engine”. SAE Technical Paper
2016-01-8091. DOI: 10.4271/2016-01-8091.
24.
US4013048: F02B 75/28. Bourke type engine. Reitz D.M. (USA). 22.03.1977.
25.
Yuan S.
2010. “Compression stroke characteristics of single piston hydraulic
free-piston engine”. Journal of
Mechanical Engineering 46(18): 134. DOI: 10.3901/jme.2010.18.134.
26.
UA106090C2. Crank-less
engine with link mechanism (variants). Krasnikov A.V., Vetrova O.A., Vetrov
E.A. Ukraine. 25.07.2014.
27.
RU2476700C2. Con-rod-free
ice, device to convert reciprocation into rotation and vice versa. Fedorov
V.F. Russia. 27.02.2013.
28.
Edwards J. 1983. “Ceramics and the
swing beam 2 stroke diesel for the automotive engine”. SAE Technical Paper 830315: 47-54. DOI: 10.4271/830315.
29.
Kolchin A.I., V.P. Demidov. 1980. Расчет
автомобильных
и тракторных
двигателей. [In
Russian: Calculation of
automobile and tractor engines]. Moscow: High School. ISBN 978-5-06-003828-6.
30.
Geyer V.G., V.S. Dulin, A.G.
Borumensky, A.N. Zarya. 1981. Гидравлика
и
гидропривод. [In
Russian: Hydraulics and hydrodrive]. Moscow: Nedra. ISBN 5-247-01007-8.
Received 18.05.2019; accepted in revised form 19.08.2019
Scientific
Journal of Silesian University of Technology. Series Transport is licensed
under a Creative Commons Attribution 4.0 International License