Article
citation information:
Hajdučík, A.,
Škrabala, J., Medvecký, Š., Brumerčík, F. Kinematic analysis of
trapezoidal suspension. Scientific
Journal of Silesian University of Technology. Series Transport. 2019, 104, 27-36. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2019.104.3.
Adrián HAJDUČÍK[1],
Jozef ŠKRABALA[2], Štefan
MEDVECKÝ[3], František BRUMERČÍK[4]
KINEMATIC ANALYSIS OF TRAPEZOIDAL SUSPENSION
Summary. This article deals with the kinematic analysis of
trapezoidal suspension. Specifically, it focuses on the behaviour of the
chassis when obstacle crossing was monitored. Our team is developing an
autonomous mountain vehicle that will be equipped with different working
adapters such as a cutter bar and a picker. The device was designed for work on
slopes, hence, must be able to overcome certain natural obstacles. This implies
the need to analyse the wheel suspension kinematics. The vehicle was built on a
trapezoidal suspension, which has proven to be the most suitable option with
respect to operating conditions. From the results obtained, it was possible to
analyse the driving characteristics of the obstacle, track the rollover limits
and overall safety of operation.
Keywords: mountain mower,
trapezoidal suspension, obstacle
1. INTRODUCTION
The comfort of driving a car
depends on the road surface, road condition and the construction of the car
itself [14,18,19,21]. The last of these factors can reduce the adverse effects
of the other two. There are many types of constructions. The axles are the
vehicle structural elements, which connects the vehicle frame and the wheel [1,3].
The axle consists of the wheels, wheel suspension system, wheel bearing system
and optional systems: suspension, steering, drive and wheel braking [5,8,15,16].
Division of the axles:
1. Solid axles
2. Swinging (independent hanging)
axles
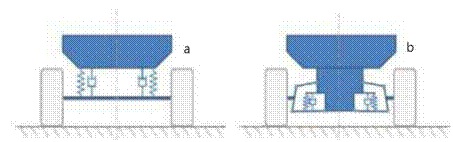
Fig. 1. a) solid axle,
b) independent hanging axle [1]
The dependent suspensions consist
of a rigid element - a beam at the end of which the wheels are attached. Hence,
the movement of the wheels is dependent as the movement of one wheel is
transmitted through the beam to the other. Thus, they are mainly used on the
rear axles of trucks and on the axles of vehicles designed to work in tough
terrains and difficult conditions [2,4,6,20]. The vertical movement of the
wheel with independent suspension does not affect the direct movement of the
opposite wheel. The advantages of independent suspension are vibration
resistance and simpler influence of vehicle properties by changing geometry, smaller
space requirements and lower weight of unspring parts [10].
Kinematic analysis was used to
calculate the positions, velocities and acceleration points of the mechanism,
regardless of the load. The design and calculation works were done with the use
of the Creo Parametric CAD system and the ADAMS system.
2. BASIC REQUIREMENTS
The proposed axle is
based on the following requirements:
• forwards /
backwards
• turning wheels
• turn around the
centre of the mower
• walk in
The following
requirements were observed as well:
• work on slopes
with a slope of up to 45°
• overcome terrain
inequalities and obstacles
• correct
positioning of the mowing device
• maintaining
agrotechnical requirements
• dampening dynamic
effects from wheel drive
• use of suitable
tires for a given use
• use of passive
suspension
• points of
attachment of the arms on the chassis
Based on these
requirements, the trapezoid axle type (two-armed) was selected. The advantages
of this type of suspension are mainly the variability in the choice of
geometric parameters, the possibility of attaching the shock absorbers and the
load distribution on the two arms. The rotating unit was above the wheel,
allowing the wheel to rotate by 90°. The advantage of the position of the
servomotor [9,10] above the wheel was to reduce the load on rotation. This
"relieving" of the servomotor was ensured by moving the axis of the
servomotor through the centre of gravity of the wheel. We tried to distribute
axle weight to the centre of gravity of the wheel, which helped to use full
tires. Other components and construction were significantly easier, making the
axle centre position in the direction of the horizontal axis y approaching the
centre of gravity of the wheel. In the direction of the axis z, from the
position of the centre of gravity, the servomotor with the gearbox was
affected. A schematic sketch of the axle can be seen in Fig. 2 [11,12,17].
2.1. Elements of the
mechanism
The main axle parts
(Fig. 2) are the chassis attachment (1), upper suspension arm (2), lower
suspension arm (3), suspension body (4), wheel attachment (5), air damper (6)
and a servomotor (8).
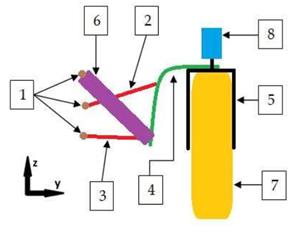
Fig. 2. Schematic sketch
of the axle [17]
To suspend the axles,
the air suspension was selected as it is more suitable for the needed application
because it has adjustable stiffness. We were able to adjust the stiffness of
the dampers by the means of the pressure in the rolls. These shock absorbers
have the possibility of complete shutdown and a choice of jump in the event of
an obstacle. Communications between the shoulders and the brick, as well as the
shoulders and the frame, are pivotable. Therefore, each joint had one degree of
freedom, which was ensured by the roller bearings [7,8].
The choice of the
geometric dimensions of the trapezoidal suspension was based on the concept of
the mower, the size of the reaction forces at the pivots of the suspension pins
and the kinematic analysis of the suspension mechanism.
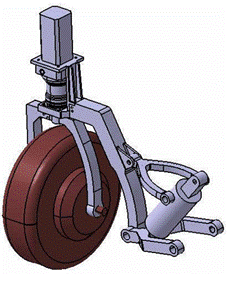
Fig. 3. Geometrical 3D
model of the axle [17]
3. KINEMATIC ANALYSIS OF
THE TASK
Before performing the
analysis, it was necessary to define the mechanism itself, create a kinematic
scheme, determine the number of degrees of freedom of the mechanism, the
correctness of the mechanism, as well as the number and type of links in order
to create a mathematical model. The input parameters of the model were the
geometric coordinates of the significant points and the suspension parameters,
which formed a set of all permissible solutions. The created kinematic model of
the mechanism has one degree of freedom. The remaining degree of freedom was
taken by defining the displacement of the DB (wheel / terrain) contact point in
the z-axis direction (Fig. 4) [17].
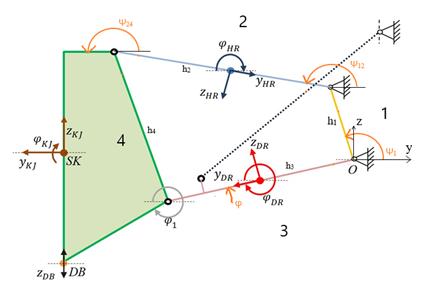
Fig. 4. Kinematic scheme
with reference points [17]
This kind of mechanism
has been analysed by different authors in various publications [3,4,13].
However, it is obvious that the mechanism of this suspension is four-element,
closed and single-loop. The Gruber's rule determines that real mobility is the
same as the theoretical one, consequently, the system is correct.
3.1.
Mathematical model
Mathematically, the
motion of a mechanism is described by nonlinear algebraic equations (NAE). Fig.
5 demonstrates that it is a closed-loop mechanism. We determined the number of
vector loops from the formula [5]
![]() . (1)
. (1)
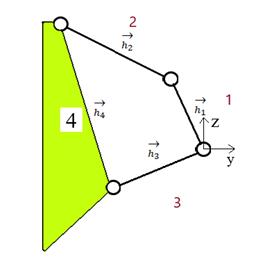
Fig. 5.
Single loop mechanism
The vector loop is then
written as the equation
![]() . (2)
. (2)
The input values were
based on the dimension requirements of a customer. The formulas derived for the
mechanism kinematic loop are defined as
y
axis: ![]() , (3)
, (3)
z
axis: ![]() . (4)
. (4)
3.2.
Solution in ADAMS
The model used for ADAMS
simulations has been adapted to suit the optimised number of moving parts,
hence, the inertia of the mechanism itself. The simplified model of a mountain
mower was developed in the Adams MSC software (Fig. 6). The input parameters of
the model were the geometric coordinates of the significant points and the hanging
axle parameters that created the set of all acceptable solutions.
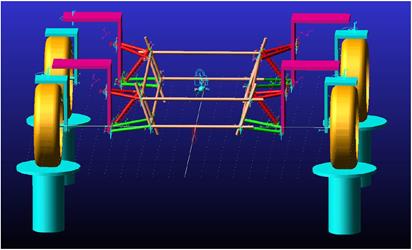
Fig. 6. Model in Adams view environment
As mentioned above, the
remaining degree of freedom was removed by defining the displacement of the
wheel contact point and the ground in the z-direction. Simulations that
represented the crossing of the mower over the obstacle were performed. The
simulation consisted of a displacement of 100 mm in the z-direction, that is,
50 mm in the positive direction and 50 mm in the negative axis direction (Fig.
7).
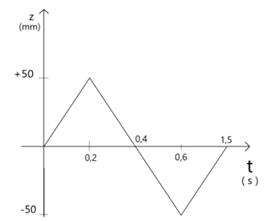
Fig. 7. Graph of actuating process (right side)
4. RESULTS
The actual
implementation of input variables was evaluated by monitored parameters /
outputs from the simulation. The outputs were specific characteristics or
features of the model that delimited a set of permissible solutions. Many
outputs were monitored for simulations. We have selected the following outputs
for this article.
The following selected
graphs reflect the behaviour of a specific point on the frame, depending on the
change of path, speed and acceleration when crossing the obstacle.
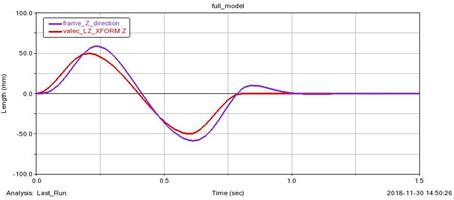
Fig. 8. Graph of track
dependence on time
The red colour curve in Fig. 8 shows dynamic excitation (by
displacement). The total displacement was 100 mm in the z-axis direction, 50 mm
in a positive and 50 mm in a negative direction.
The purple colour
illustrates the response of the vehicle gauge in the direction of z-axis.
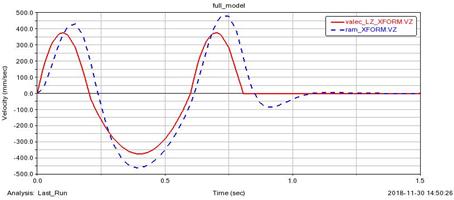
Fig. 9. Time - velocity dependence
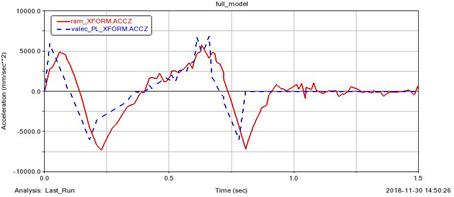
Fig.
10. Time - acceleration dependence
Figure 11 shows the maximum compression
or stretching of the spring. During the passage of the wheel through the
obstacle, the force effects on the springs were monitored.
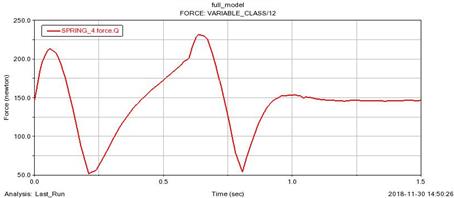
Fig. 11. Spring force
during simulation
5. SUMMARY
The kinematic analysis
in MSC Adams demonstrates the possibilities of applying different types of
suspension. Extreme conditions for safe operation when crossing obstacles were
identified. Solution results were verified on a second mower prototype (MM2).
All tests were successful. Furthermore, other tests are ongoing at the time of
preparation of this article.
The first part of this
article provides information on axle types and the choice of the appropriate
axle type. The selected axle appears to be the most appropriate for (MM2) as
confirmed by tests. The initial conditions that influenced the formation of the
suspension were defined. In the next section, the principle of creating a
mathematical model was presented. Thereafter, an overview of some test results.
Acknowledgement
The
research is supported by the Cultural and Educational Grant Agency of the
Ministry of Education, Science, Research and Sport of the Slovak Republic under
project No. 046ŽU-4/2018.
References
1.
Amirouche
F. 2007. Fundamentals of Multibody
Dynamics: Theory and Applications. Springer Science &
Business Media. 684 p. ISBN 08-1764-406-7.
2.
Avesh
Mohd, Rajeev Srivastava. 2018. “Parametric optimization to design a
passenger car suspension system for better dynamic performance”. European Transport/Trasporti Europei
71(paper 1): 1-14.
3.
Bulej V., J. Stanček, I. Kuric, I. Zajačko. 2017. „The space distribution and transfer of
positioning errors from actuators to the TCP point of parallel
mechanism”. Machine Modelling and
Simulations 2017 (MMS 2017). ISSN 2261-236X. London: Édition
Diffusion Presse Sciences, 2018. Available at:
https://www.matec-conferences.org/articles/matecconf/pdf/2018/16/matecconf_mms2018_02006.pdf.
4.
Caban J., P. Drozdziel, J. Vrábel, B. Šarkan, A.
Marczuk, L. Krzywonos, I. Rybicka. 2016.
„The research on ageing of glycol-based brake fluids of vehicles in
operation”. Advances in Science and
Technology 10(32): 9-16.
5.
Caban
J., A. Marczuk, B. Šarkan, J. Vrábel. 2015. „Studies on
operational wear of glycol-based brake fluid”. Przemysł Chemiczny 94(10): 1802-1806.
6.
Dahil
L. 2017. “Effect on the vibration of the suspension system”. Metalurgija
56(3-4): 375-378.
7.
Faturík Lukáš, Libor
Trško, Slavomír Hrček, Otakar Bokuvka. 2014. „Comparison of structural design in high and ultra-high cycle
fatigue regions”. Transactions of
FAMENA 38(4): 1-12. ISSN 1333-1124.
8.
Figlus
Tomasz, Mateusz Koziol. 2016. „Diagnosis of early-stage damage to polymer - glass fibre
composites using non-contact measurement of vibration signals”.
Journal of Mechanical Science and
Technology 30(8): 3567:3576. ISSN 1738-494X. DOI: 10.1007/s12206-016-0717-1.
9.
Glowacz Adam, Zygfryd Glowacz. 2017.
„Diagnosis of the three-phase induction motor using thermal
imaging”. Infrared physics &
technology 81: 7-16. ISSN 1350-4495. DOI: 10.1016/j.infrared.2016.12.003.
10.
Glowacz Adam, Zygfryd Glowacz. 2017.
„Diagnosis of stator faults of the single-phase induction motor using
acoustic signals”. Applied acoustic
117A: 20-27. ISSN 0003-682X. DOI: 10.1016/j.apacoust.2016.10.012.
11.
Kelemen
M., I. Virgala, T. Lipták, Ľ. Miková, F. Filakovský,
V. Bulej. 2018. „A
novel approach for a inverse kinematics solution of a redundant
manipulator”. In: Applied
Sciences-Basel (Special Issue "Advanced Mobile Robotics") 8(11),
2229: 1-20. ISSN 2076-3417. Available at: https://www.mdpi.com/2076-3417/8/11/2229.
12.
Kohár
Róbert, Slavomír Hrček. 2014. „Dynamic analysis of a
rolling bearing cage with respect to the elastic properties of the cage for the
axial and radial load cases”. Communications
– Scientific Letters of the University of Zilina 16(3A): 74-81. ISSN
1335-4205.
13.
Koziol
Mateusz, Tomasz Figlus. 2017. „Evaluation of the failure progress in the
static bending of GFRP laminates reinforced with a classic plain-woven fabric
and a 3D fabric, by means of the vibrations analysis”. Polymer Composites 38(6): 1070-1085.
14.
Krayushkina
Kateryna, Olegas Prentkovskis, Andrii Bieliatynskyi, Raimundas Junevičius.
2012. “Use of steel slags in automobile road construction”. Transport 27(2): 129-137.
15.
Palčák
František. Theory of mechanisms.
Bratislava. SVŠT, 1993. 168 p. ISBN 802270-531-4.
16.
Skrúcaný Tomáš, Branislav
Šarkan, Tomasz Figlus, František Synák, Ján
Vrábel. 2017. „Measuring of noise emitted by moving vehicles”. MATEC Web of Conferences 107: 00072.
ISBN: 978-1-5108-4114-7. DOI: https://doi.org/10.1051/matecconf/201710700072.
17.
Škrabala
Jozef. 2018. „Design of the remote controlled mower“. Diploma
thesis. Bratislava: Slovak University of Technology in Bratislava.
18.
Sobota Aleksander, Renata Żochowska, Emilian
Szczepański, Paweł Gołda. 2018. „The influence of tram tracks on car
vehicle speed and noise emission at four-approach intersections located on
multilane arteries in cities”. Journal
of Vibroengineering 20(6): 2453-2468.
19.
Staniek
M., P. Czech. 2018. “Self-correcting neural network in road pavement
diagnostics”. Automation in
Construction 96: 75-87.
20.
Thomas
D.G. Fundamentals of vehicle dynamics.
society of automotive engineers. 1992. 495 p. ISBN 1560911999.
21.
Valaskova
V., D. Papan, R.C. Barros. 2016. “Assessment of the roadway dynamic
response due to the tatra 815 lorry excitation and experimental
verification”. Komunikacie 4.
ISSN: 2585-7878.
Received 03.06.2019; accepted in revised form 19.08.2019
![]()
Scientific
Journal of Silesian University of Technology. Series Transport is licensed
under a Creative Commons Attribution 4.0 International License