Article
citation information:
Čuboňová, N.,
Dodok, T.. Ságová, Z. Optimisation of the machining process using genetic
algorithm. Scientific Journal of Silesian
University of Technology. Series Transport. 2019, 104, 15-25. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2019.104.2.
Nadežda ČUBOŇOVÁ[1],
Tomáš DODOK[2],
Zuzana SÁGOVÁ[3]
OPTIMISATION
OF THE MACHINING PROCESS USING GENETIC ALGORITHM
Summary. This paper deals with genetic algorithms as an
optimisation method and its use for optimisation of the machining process in
the CAM system. Tool path verification and optimisation are two best ways of dramatically improving manufacturing operations while
saving money with relatively little work. Genetic algorithms can be used for
improvement of these operations and considerably reduce length of tool paths
leading to the reduction of machine times and optimisation of cutting
parameters. Provides the software application created to optimise processes of
boring and local milling (Incomplete sentence; what or who provides).
Keywords: optimisation, genetic
algorithms, CAM system
1. INTRODUCTION
Preparatory activities
of the pre-production stage and their importance in terms of affecting the
quality and price of produced parts constitute a huge space for the application
of the philosophy of optimisation.
The problems associated with optimisation of technological processes are
increasingly relevant given the opportunities of accessible solutions and use
of computer technology [4,11]. Automated plants with deployed CNC technology
utilise PC at the design stage, with subsequent transition to technology, using
the CAD/CAM software. When solving optimisation tasks related to technological
processes, it is necessary to optimise not only operations but also the used
technological devices defined within the technological process operation
segments to ensure maximum labour productivity and minimum costs or maximum
profit. The modern concept of CAD/CAM systems enables optimising the process by
a number of criteria. Optimisation can be based, for example, on a semi-finished product. The
semi-finished product in a CAD/CAM system is gradually updated (modified)
during the design and simulation of the machining process [10]. Each following
operation includes machining of the remaining material only. This means
elimination of unnecessary and inefficient movements and actions [12]. Computer-aided
optimisation of machining processes (CAM – computer-aided manufacturing)
utilises software applications where the method of performance is usually
carried out using additional modules (optimisation programs). Optimisation
programs enable maximisation, in the machining process, especially tool paths,
cutting parameters, NC programs, etc., [13]. However, the tool path generated
from CAD/CAM systems is not guaranteed as the optimal tool path and there are
possibilities that the tool path distance is longer in order to complete each
drilling process. Therefore, optimisation of the CNC machine tool path should
be done before starting a machining process to ensure the tool path taken will
produce the shortest path of cutting tool travel [1].
Optimisation of machining processes
plays a key role in meeting the demands for high precision and productivity.
The primary challenge for machining process optimisation often stems from the
fact that the procedure is typically highly constrained and highly non-linear,
involving mixed-integer-discrete-continuous design variables. Additionally,
machining process models are likely discontinuous, non-explicit, or not
analytically differentiable with the design variables. Traditional non-linear optimisation techniques are mostly
gradient-based, which poses many limitations on their application to
today’s complex machining models. Mathematic analysis disposes of a
large variety of mathematic models for solving a large variety of optimising
problems. Nevertheless, many real-world tasks cannot be solved by these techniques,
or their solutions, which are not as good as those of some other special
nonlinear optimisation techniques. Therefore, some special optimisation
techniques were designed as solutions close to the optimal one but search only
in a very little fragment of the solution space. One of such optimisation
technique is the Evolution Programming (EP). EP is the name of a large variety
of optimisation techniques based on evolution principles. Genetic algorithms
(GA) is one of these evolution techniques, which mostly imitate principles of a
natural evolution process. GA presents itself as a very strong optimisation
technique capable of solving very complicated task with large search space in a
very short time with very good results. There is a lot of application, wherein
any optimisation technique was used or another whose results can be improved.
The field of application of genetic algorithms towards solving optimisation
problems in engineering is almost unlimited. [2]. Prediction
solutions optimisation problem depends on the correctness of the proposed
action solution to a specific optimisation task. This involves determining the
optimisation criteria and restrictive conditions, relating to the case and
knowledge of the issue of genetic algorithms, which outwardly look like a
universal solution, but requires an individual approach to each case.In
conjunction with the Genetic Algorithm (GA) method, Kumar and Pacahauri [5] and
Nabeel et al. [9] also used the Travelling Salesman Problems (TSP) to reduce
the total time and distance of tool travel for drilling sequence. Finally,
genetic algorithm is presented in this paper as an optimisation method with its use for the
maximisation of the machining process in the CAD/CAM system. It is a software
application with the possibilities of crossing methods especially with TSP,
created to optimise the processes of boring and local milling.
2. GENETIC ALGORITHM (GA) IN BRIEF
Concisely stated, a
genetic algorithm (GA) is a programming technique that mimics biological
evolution as a problem-solving strategy. The evolutionary program is a probabilistic algorithm which manages
the population of "n" individuals (chromosome) for "t"
iterations. Each individual represents a potential solution to the problem and
within the evolutionary program, it is presented as a data structure. Each
solution is evaluated, and the result of the evaluation is a degree of
suitability (fitness). The new population is then created selecting the most
suitable individuals. Some of the individuals undergo the transformation using
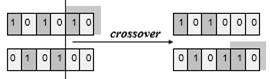
genetic operators and generate new solutions. There are single-transformations
of mutation type (Fig. 1a) which will
create a new individual through a small change in the structure itself and
transformations of higher-order of crossover
type (Fig. 1b), which will create a new individual combining parts of two
or more individuals. After a certain number of generations, the program
converges supposing that the best individual represents a nearly optimal
solution [7].
|
|
|
Fig. 1. Scheme of
mutation (a), and single point
crossover (b) [6]
For a specific task,
several evolutionary programs can be proposed. These can differ in many ways.
Different ways of the individual´s
inscriptions can be used, genetic operators of individuals´
transformation can also differ similarly as methods of creating the initial
population or management methods of restrictive conditions and parameters
(population size, the probability of using genetic operators, etc.). However,
all of them share basic principles, for example, the population of individuals
undergoing some transformations (changes) and the individual struggle for
survival during the process of evolution.
The best-known techniques
among evolutionary algorithms are the
climbing technique also known as local or neighbouring search, the simulated annealing technique and genetic algorithms that truly mimic
evolutionary principles in nature. Before a genetic algorithm can be put to work on any
problem, a method is needed to encode potential solutions to that problem in a
form that a computer can process. These are the most common methods for
solution encoding: binary string
(0’s and 1‘s), string of
values (integer, real, letter...), string
encoded as permutation (every value can appear in the string only once), branching data structures (trees), and matrix encoding. It must be taken into
consideration that solution strings of evolutionary algorithms need not have a
fixed length. Then, a selective mechanism would be applied to decide which
individuals will be fit for selection for reproduction and which, on the other
hand, will be discarded as unfit. There are many different techniques which can
be used when creating a genetic algorithm for selecting the individuals to be
transferred to the next generation; Elitist selection, Fitness-proportionate
selection, Roulette-wheel selection, Scaling selection,
Tournament selection, Rank selection, Generational selection, Steady-state
selection, and Hierarchical selection. Some of these methods are used
individually, while others can be and are often used in combination.
Population size is a very important factor that
influences the function of genetic algorithms. If the population is too small,
the genetic algorithm can converge very quickly. However, if is too large, the
genetic algorithm may require too much computational time, which makes it
inefficient. In addition, the population diversity and selection pressure are
influenced by the population size. An algorithm with varying population size
does not use any of the earlier mentioned or similar selective mechanisms,
rather it evaluates individuals by age.
Age of the individual is equivalent to the number of
generations during which the individual will be in the population managed
by the algorithm. The individual´s age is proportional to its fitness and
replaces thereby selective mechanisms. However, it also directly influences the
population size in every step of the evolutionary process. This method
describes the real natural selection in the most convincing manner. Lifetime
(or age) is assigned to each individual at its origin and remains constant
during the evolutionary process until its extinction. This means that the
individual´s age is no longer recalculated. There are many ways of
assigning age to individuals. It is obvious that the assignment of a constant
value (greater than 1) would result in the population exponential increase.
Equally, as there is no selection pressure on individuals, the assigning of
constant age would result in a low-efficiency algorithm. Several strategies for
the calculation of the age of individuals have been proposed and tested
experimentally, for example [8]:
Proportional allocation:
![]() (1)
(1)
Linear allocation:
![]() (2)
(2)
Bi-linear
allocation:
![]()
![]() (3)
(3)
![]()
![]() (4)
(4)
Fitness (i) - fitness of the
individual
AvgFit - average fitness in
the current population
MinFit - minimal fitness in
the current population
MaxFit - maximal fitness in
the current population
MinLT - minimal lifetime value
MaxLT - maximal lifetime
value
LT - lifetime value
![]() (5)
(5)
Proportional evaluation - This originated from the idea of
roulette selection; the age of the individual is proportional to its fitness.
However, this evaluation has one great shortcoming; individuals, whose fitness
greatly exceeds the average fitness, can be evaluated by very old age. Linear evaluation - the life of
individuals is recalculated to the best suitability in the population. If,
however, many individuals have the same rate of fitness, or near the maximum,
this leads to a high evaluation and rapid expansion of the population. Bi-linear evaluation is a compromise
between the previous two. It highlights the differences between the life
expectancy of the best individualswhile taking into account the maximum and
minimum length of life [8].
When selecting suitable
individuals, they must be randomly modified in the hope that the fitness of the
next generation will increase. Two methods are used for searching the problem space,
namely: exploitation
- when creating a new generation, it makes use of the "experiences"
of previous generations to determine areas promising success in searching
optimal solutions; but it carries the risk of being trapped in a local extreme;
exploration - when creating a new generation it ignores the
"experiences" of previous generations. The browsing process is
conducted in unexplored areas thus avoiding deadlocks in a local extreme, which
eventually slows down the process. During the browsing itself, the main function of the
algorithm is to find the global extreme of hypersurface and not get stuck in any
of the local extremes during the searching process. Local extremes usually work
in parallel with several individuals making up the population. This is a
discrete time process – individual generations gradually take turns. The
process is repeated until the terminating condition is fulfilled. It may be the maximum number of
generations or other acceptable limit. The fundamental principle of the
genetic algorithm activity is shown in the flowchart (Fig. 2):

Fig.
2. Flowchart of genetic algorithm [7,14]
Genetic algorithms are
highly effective means of optimisation and are applied mainly for the solution
of problems with large or infinite number of solutions. Such a problem may be,
for example, the determination of an optimal drilling path when the tool path
passes through n points. Similar tasks can be found in many optimisation
techniques called Travelling
Salesman Problems (TSP) [7], a special type of problem, which evolutionary
algorithms deal with. Definition of this task is very simple: the salesman has
to visit each place within his trading area once and then return to the
starting city. If he knows the cost of travelling among individual cities, how
should he plan the tour for minimal costs? The search space is then the
permutation of n cities; every
permutation is then one possible solution and the optimal solution is the
permutation with minimal travelling costs. Size of the search space is then n! TSP is a relatively old problem:
Euler first described it in 1759 (under a different title). The name
“Travelling salesman” was first used in 1932, in a German book: Travelling salesman, how and what to do in
order to obtain commission and be successful in his trade [8]. The RAND
Company presented TSP in 1948. The good reputation of this company helped the
TSP become a famous and popular topic. In recent times, many algorithms have
been designed for TSP solution using different methods and strategies.
TSP problem can be
applied for optimisation of some technological processes such as drilling and
local milling operations. Most of the common CAM and CAD/CAM systems use none
or only some type of linear mathematics
for the solution of similar tasks due to long computing time [3]. Due to its
efficiency, GA can solve the mentioned problems within few minutes with
brilliant results. Thanks to their fundamental functions and characteristics as
parallelism, schema theorem and crossing,
it is possible to create various optimisation applications.
3. GA APPLICATION IN OPTIMISATION
OF MILLING AND DRILLING PROCESS IN CAD/CAM
The Toolpath Optimiser
application was designed for the best use of tool paths of drilling and local
milling based on GA. During the design and creation of the genetic algorithm
for the Toolpath Optimizer application, it was necessary to choose among many
techniques and settings (for example, a problem inscription, method of
crossover, selection and mutation, setting the probability of crossover and
mutation, setting the size of population), by means of which the genetic
algorithm could be assembled. Incorrect set up of a genetic algorithm could
lead either to a too long optimisation process or to an unsatisfactory result
of the optimisation process. The set-up genetic algorithm was implemented as an
optimisation instrument for particular inputs and outputs (CL data from Creo
Parametric 5.0) for created Toolpath Optimiser applications. The application
was developed in the programming environment Borland Delphi, supplemented by
the module for reading and writing of CL data, and finally experimentally
validated on concrete examples of drilling and local milling. It also includes
a function for the movement of the approaching point before drilling, which
reduces inaccuracies of tool positioning caused by a backlash in the slides.
Input and output data of the optimisation module are CL data of CAD/CAM system
Creo Parametric 5.0. The experimental verification of the created optimisation software was applied to
maximise the creation of the technological process of the parts shown in Fig.
3a, b.
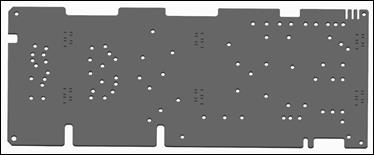
The problem of drilling optimisation can also be found
in the electrotechnical industry in the production of circuit boards, and many other areas. The reason this
problem is often solved in the production of circuit boards is that the
drilling process itself is very short. Movement of the tool out of contact with
the machined surface presents an essential part of the production time. The second
reason is the number of holes, that is, to find the optimal path for more than 20
points (Fig. 3a) becomes an almost unrealistic task under conditions of common
practice [13].
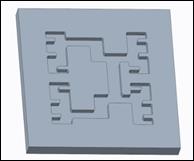
Local milling is an operation that is performed
after a previous operation of volume milling with a larger diameter tool (Fig.
3b). In places where a larger diameter tool could not remove the material, a
smaller-diameter tool is used; this operation is called local milling. High
requirements demand precision, and in drilling, the moving towards the centre of holes under the same vector is often
applied. This helps eliminate inaccuracies caused by changes in the slides
movement or movement of a machine table from positive to negative and vice
versa. The application controls the tool path so that the tool approaches the
positions of all holes under the same vector.
|
a) |
b) |
Fig. 3. Illustrations a) of printed
circuit boards for holes manufacturing by drilling operation, b) of local milling operation
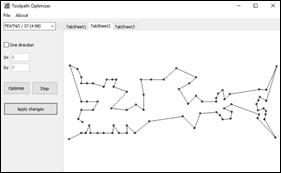
A non-optimised tool
path for the drilling process is generated with the system Creo then
transformed into the CL data file and, subsequently, loaded into the Toolpath
Optimiser application. Fig. 4a shows a tool path of the drilling process
generated by the system Creo and Fig. 4b shows the non-optimised tool path
loaded into the Toolpath Optimiser application.
|
a) |
b) |
Fig. 4. a) non-optimized tool path of the
drilling operation generated by the system Creo b) non-optimized tool path
loaded in the application Toolpath Optimizer
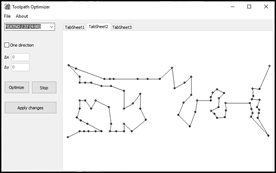
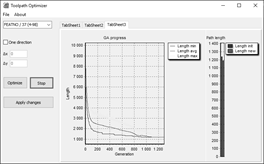
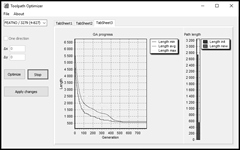
Optimisation process in
the application starts with the confirmation of the selection sequence. Its
graphical flow is shown in two tabs (Fig. 5). One shows the best path in each
step of the evolutionary process (Path
length) and the other gives graphical information about the evolutionary
process (GA process). GA process
shows the dependence of the found shortest path on the number of generations (Length min). It also shows the
dependence of the average path length of all individuals from a particular
generation on the number of generations (Length
avg) and the dependence of the found longest path in the generation on the
number of generations (Length max). Path
length graphically displays the original length of a toolpath generated
from the CL data file (Length init)
and a new optimised path length (Length
new) generated by GA. When the evolutionary process is completed, it is
possible to compare the length of the new and original path, to compare the
optimised path (Fig. 5), to decide whether the result meets the requirements or
to repeat the evolutionary process.
|
|
Fig. 5. Graphical flow
of the optimisation process at the drilling operation
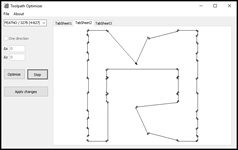
Having accepted the
optimised path (Fig. 6a), the CL data file is edited. The optimised tool path
can be loaded and displayed in Creo (Fig. 6b) and consequently processed by the
post-processor to NC code for a particular CNC machine.
|
a) |
b) |
Fig. 6. a) optimised tool path generated by
the application Toolpath Optimiser, b) optimised tool path of
the drilling operation loaded in the system Creo
|
|
|
||
|
a) |
b) |
|
|
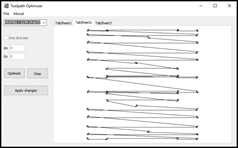
Fig. 7. Tool path of
a local milling operation.
a)
non-optimised
tool path generated by system Creo,
b) optimised tool path loaded in the application Toolpath Optimiser
From the point of view
of tool rapid traverses, the local milling process is similar to the process of
drilling. Both processes use the same genetic algorithm, the only difference is
in the work of CL data field. Fig. 7 shows a simple example of tool path optimisation
process using the Local Mill sequence
in CAD/CAM system Creo, at Fig.7a is an original non-optimised tool path
generated by the system Creo; Fig.7b shows the same tool path optimised by the Toolpath Optimiser. The graphical flow
of the optimisation process at the milling operation is depicted in Fig. 8. The
genetic algorithm which forms the core of the Toolpath Optimiser proved to be a
highly effective means of optimisation. The result may be considered highly
satisfying. With smaller optimisation tasks - about twenty points - the
optimisation process takes only a few seconds [6].
|
|
Fig. 8. Graphical flow
of the optimisation process at the milling operation
4. CONCLUSION
To successfully address
an optimisation problem, we must know optimisation methods and appropriately
select the method we want to deploy to solve the problem in question. Although
some methods resemble one another due to their work processes, they may not be
equally suitable for solving the given task. Improper use of a method can
reduce the resulting effect of its work; it can even lead to obtaining false
results. TSP
problem can be applied for some of the technological processes such as
drilling, boring or local milling operations. Most of the common CAM and
CAD/CAM systems do not use any optimisation technique or use some kind of
linear mathematics based technique for solving this task due to the computing
time [7]. GA due to their
efficiency can solve the mentioned problems in a few minutes instead of a long
time (hours, days) with remarkable results. This article details optimisation
of machining processes using out of the CAD/CAM system environment. This
optimisation module may be used either directly or it can easily be modified in
compliance with the users´ requirements. For example, it is possible to
change the module of input and output data, which currently works only with the
CL data field of CAD/CAM system Creo. The experiments were created to optimise
processes of both boring and local milling. The results of these experiments
show that genetic algorithm is a simple and effective method for solving
complex optimisation problems. From the practical point of view, the
application Toolpath Optimiser can be used in the pre-production phase with the
aim to increase productivity and reduce production costs.
References
1. Abdullah
Haslina, Ramli Rizaudin, Abd Wahab Dzuraidah, J.A. Qudeiri.2015. “Simulation
approach of cutting tool movement using artificial intelligence method”. Journal
of Engineering Science and Technology 10 (Spec. Issue on 4th International
Technical Conference (ITC) 2014): 35-44. ISSN: 18234690.
2.
Bhoskar Trupti, Omkar K. Kulkarni, Ninad K. Kulkarni, Sujata L. Patekar,
G.M. Kakandikar, V.M. Nandedkar. 2015. „Genetic algorithm and
its applications to mechanical engineering: a review”. In: Materialstoday
Proceeding, 4th International Conference on Materials Processing and
Characterization 2 (4-5): 2624-2630. ISSN 2214-7853. DOI: https://doi.org/10.1016/j.matpr.2015.07.219.
3.
Jakubovičová Lenka, Milan Sága. 2014.
“Computational analysis of contact stress distribution in the case of
mutual stewing of roller bearing rings”.
Novel Trends in Production Devices and
Systems, Applied Mechanics and Materials 474: 363-368. Zürich: TransTech Publications. ISBN
978-3-03785-944-5. ISSN 1660-9336.
4. Karpavičius
Paulius, Vytautas Ostaševičius, Vytautas Jūrėnas, Jolantas
Baskutienė. 2017. „Self-powered wireless sensor system
application for cutting process control”. Mechanika 23(3): 456-461.
5. Kumar Abdhesh, Pachauri
Praveen. 2012. „Optimization drilling sequence by genetic
algorithm”. International Journal of Scientific and Research Publications 2(9): 1-7. ISSN 2250-3153.
6. Michalco Miroslav. 2009. “Implementácia
genetických algoritmov pri riešení
optimalizačných úloh technologických procesov”.
PhD.thesis. ŽU
v Žiline, SjF, KAVS. [In Slovak: Implementation of genetic
algorithms into solving of optimization task. PhD.thesis.
University in Žilina,Faculty of Mechanical
Engineering].
7. Michalco Miroslav, Nadežda Čuboňová. 2009.
“Computation methods for travelling salesman problem”. In: TRANSCOM 2009. 8th European
Conference of Young Research and Scientific Workers: 141-144. University of
Žilina, Mechanical Engineering Technologies, Žilina, Slovakia. 22-24
June 2009, ISBN 978-80-554-0042-6.
8. Michalewicz Zbigniew.1999. Genetic Algorithms+Data Structures=Evolution
Programs. Berlin: Springer. ISBN 3-540-600679-9.
9. Nabeel Kadim Abid Al-Sahib,
Abdulrazzaq Hasan Fahad. 2014. „Tool path optimization
of drilling sequence in CNC machine using genetic algorithm”. Innovative Systems
Design and Engineering 5(1): 15-26. ISSN 2222-1727.
10. Náprstkova Nataša.
2010.“Students connecting to production problems resolutions in CAD/CAM area”.
In: 9th International Scientific Conference:
Engineering for Rural Development: 310-314.
Jelgava, 27.-28.05.2010. ISSN 1691-5976.
11. Ostasevicius V., V. Jurenas, A.
Juskevicius. 2014. „Modified tool structures for effective
cutting”. Mechanika 2:
171-176.
12. Sága Milan, Roman
Bednár, Vaško Milan. 2011.
„Contribution
to modal and spectral interval finite element analysis”. In: 10th Biennial International Conference on
Vibration Problems (ICOVP). Prague, Czech Rep. Book Series: Springer Proceedings in Physics 139:
269-274. DOI: 10.1007/978-94-007-2069-5_37.
13. Sága Milan, Milan Vaško, Nadežda
Čuboňová, Wiesława Piekarska. 2016. Optimisation algorithms in mechanical engineering applications.
Harlow: Pearson. ISBN 978-1-78449-135-2.
14. The TalkOrigins Archive.
“Genetic Algorithms and Evolutionaty Computation”. Available at:
http://www.talkorigins.org/faqs/genalg/genalg.html.
Received 19.05.2019; accepted in revised form 18.08.2019
![]()
Scientific
Journal of Silesian University of Technology. Series Transport is licensed
under a Creative Commons Attribution 4.0 International License