Article
citation information:
Aghelfard, A., Rohanimanesh, M.S.,
Vatanshenas, A. Investigating the performance of bridges equipped with elastomeric
bearings reinforced with fibre under traffic and seismic loads. Scientific Journal of Silesian University of
Technology. Series Transport. 2019, 104,
5-14. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2019.104.1.
Arian AGHELFARD[1],
Mohammad Sadegh ROHANIMANESH[2],
Ali VATANSHENAS[3]
INVESTIGATING
THE PERFORMANCE OF BRIDGES EQUIPPED WITH ELASTOMERIC BEARINGS REINFORCED WITH
FIBRE UNDER TRAFFIC AND SEISMIC LOADS
Summary. The seismic elastomeric bearings reinforced with
fibre is considered as a new technology in comparison to other conventional
isolator systems in civil engineering. In this type of bearing, recycled fibres
replaced traditional steel plates used in common bearings. Therefore, this type
of bearing has been studied in recent years due to both environmental and
cost-saving advantages. The shortage of references about the application of this
type of bearing in the bridge industry, and particularly the continuous-span
bridges, prompted the researchers in this study to investigate the performance
of the isolated reinforced concrete box girder bridges with continuous spans.
Reducing the acceleration transmission from the substructure to the
superstructure is one of the main advantages of using seismic bearings. Based
on the study of the structural models, it was found that, in most cases,
elastomeric bearings reinforced with fibres showed a suitable performance and
reduced the acceleration applied to the superstructure by absorbing the
earthquake energy.
Keywords: box girder bridges,
multi-span bridges, near-field earthquakes, safety in transport, seismic
isolation, traffic loading, vibration engineering
1. INTRODUCTION
With the development of
transportation networks, the importance of bridges has increased drastically
with the growth in population. Due to the transfer of traffic load, bridges are
regarded as important elements of transportation systems. Seismic isolation can
be considered as the most important strategy to improve the seismic performance
of bridges. The assessment of bridges affected by the near-field earthquakes
with large pulses indicates that the seismic response values of bridges are
significantly greater than those obtained by a few pulse recordings [1].
Research on the near-field earthquakes began in the late 1970s, however, more
attention was paid to its effects on structures, particularly, bridges after
the 1990s. Hausner and Hudson were among the first to study this issue. They
concluded that the vulnerability of bridges under the near-field earthquakes,
even for an average peak ground acceleration (PGA) and earthquake magnitudes
was a remarkable value [2]. Investigating the characteristics of the earthquake
spectrum in some of the near-field earthquakes, including the duration and
frequency, revealed that the impacts due to the near-field earthquakes were
very effective on the structure response [3]. Investigation of the dynamical
performance of a bridge with reinforced concrete piers under several near and
far-field records the PGA of which were scaled to the same value, showed that
in the far-field earthquakes, the base shear force and ductility of the
structure decreased compared to the near-field earthquakes [4]. Near-field
earthquakes include critical pulses. Although these earthquakes may have small
magnitudes in Richter, they have a high potential of damage [5, 6, 7].
Experimental studies show that the
seismic elastomeric isolators reinforced with fibres can be considered as a
suitable choice in structural engineering. When this type of bearing
experiences a lateral displacement, parts of its upper and lower sides are
separated from the supporting surfaces and the isolator experiences a semi-roll
lateral deflection, reducing the effective lateral stiffness of the isolator,
and thereby increase of the isolator period, enhancing its efficiency as a
seismic isolator. Lateral stiffness is one of the most important mechanical
characteristics of seismic isolators. Given the lack of flexural strength in
the fibre reinforcement layers and the absence of steel sheets, seismic
elastomeric bearings reinforced with fibres exposed to lateral loading go under
the unique lateral roll deflection. However, it is noteworthy that in
elastomeric seismic bearings reinforced with fibres, if the ratio of bearing
height to size is less than a certain value, the reduction in the effective
stiffness due to the torsional deflection may cause instability [8]. Another
advantage of this type of isolator is its energy absorption due to the internal
interaction between the elastomeric layers and the fibre reinforcement [9].
Moreover, the application of fibre bearings due to the use of cheaper materials
when compared to other types of seismic isolators is economically advantageous.
2. VERIFICATION
In this section, the
verification of modelling was accomplished by comparing the hysteresis
performance of the bearing modelled by the authors with the experimental
results obtained in one of the recent studies. In the experiments conducted,
the researchers designed and produced samples of fibre reinforced elastomeric
isolators in certain dimensions and placed them under vertical loading and
lateral force. The bearing was located inside a hydraulic jack, with a fixed
lower plate and a 1.6 MPa pressure load applied on its upper plate. In
addition, in the horizontal direction, the cyclic loading was performed in such
a way that the bearing experienced strain values of 25, 50, and 100%,
respectively (Figure 1) [10]. In the
course of the findings, the researchers exploited the elastomeric
seismic bearings reinforced with fibres with the specifications listed in Table
1, including the total thickness of the bearing (H), the total thickness of
elastomer layers (Tr), the number of reinforcing layers (ns),
the number of elastomer layers, including the top and bottom cover layers (nr),
the thickness of reinforcing fibre plates (tf), the thickness of the
top and bottom cover layers (tc), the thickness of the middle
elastomer layers (tr), the width (a), and the length (b). The
schematics of the bearing on which the test was carried out is demonstrated in
Figure 2. The effective stiffness and damping ratio were also considered to be
as 2.248 kN/mm and 0.085, respectively. As depicted in Figure 3, the hysteresis
and the experimental graphs exhibit an acceptable resemblance.
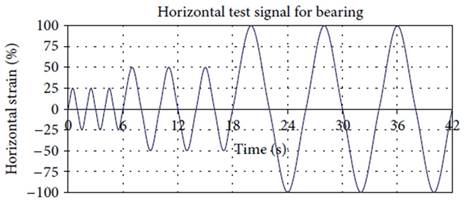
Fig. 1.
Lateral loading applied to the sample for verification [10]
Tab. 1
Specifications
of the examined bearing
|
H |
Tr
(mm) |
nr |
ns |
tf
(mm) |
tc
(mm) |
tr
(mm) |
b (mm) |
a (mm) |
|
50.75 |
50 |
7 |
6 |
0.125 |
5 |
8 |
400 |
250 |
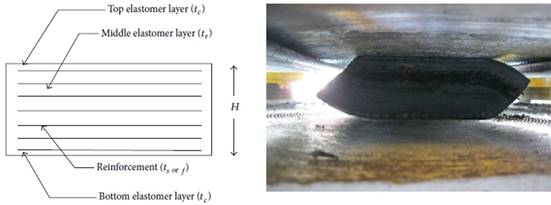
Fig. 2.
Components of the bearing [10]
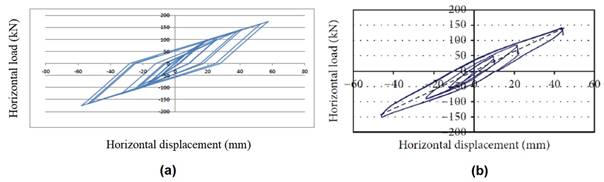
Fig. 3.
Comparison of the hysteresis diagrams obtained in this study (a) and the
experimental results (b) [10]
3. SELECTION OF APPROPRIATE
EARTHQUAKES FOR TIME HISTORY ANALYSIS
Time history analysis is a type of dynamic analyses
of structures. In this method, the effect of earthquake excitation on a
structure is measured more realistically compared to other analytical methods.
However, due to the more complex and difficult details of this method,
engineers often use this method only for designing of special and important
buildings. The earthquakes chosen to conduct time history analysis should have
characteristics similar to the probable earthquake in the area under study.
These characteristics include magnitude, distance from the epicenter, fault
mechanism, and soil type. In this study, according to Table 2, five earthquakes
with magnitudes ranging from 6 to 7.14 Richter, in near-fault regions, all
having a fault mechanism of strike-slip type, were employed. The shear wave
velocity of the studied zone was also considered to range from 375 to 750 m/s
at a distance of 30 m depth of the ground. To perform the time history
analysis, two horizontal records perpendicular to each other were used for each
selected earthquake. Furthermore, considered earthquakes were scaled according
to [11].
One of the most important limitations considered for
the selection of earthquakes was the “Significant duration”. In the
occurrence of an earthquake, the measured time from the start of data recording
by the accelerometer until the moment of ending the recording is called the
earthquake duration. However, the major oscillations of the earthquake are more
important in an interval of this time, so that in the intervals before and
after this time, the earthquake accelerations are negligible. Investigation of
the significant duration of earthquakes was carried out in two ways, the enclosed
duration and the arias intensity method. The enclosed duration method is
calculated in such a way that the time interval between the first and the last
time the acceleration values obtained from the motion of the earth exceed a
certain value, which is usually equal to the absolute value of 0.05 g. The
resulting value is the earthquake significant duration. It is remarkable that
this method has an approximate and simple nature, that is, in the limited
moments of the acceleration record, significant pulses may occur, making it
difficult to interpret the significant duration through this method. Therefore,
in this study, the second method (arias intensity) was observed to achieve
results that were more accurate. Scientifically, this method is more valid than
the enclosed time method, and its results are more reliable. In this approach,
the interpretation is performed on cumulative energy diagrams of earthquake
records. Additionally, the time interval in which the accumulated energy due to
the earthquake has a certain amount (usually between 5-95%) regarded as the
earthquake significant duration. After examining the two methods above, all the
earthquakes selected had minimum significant duration of 10 s. For better
understanding, the graphs associated with the two methods are displayed for one
of the components of the Imperial Valley earthquake (Figure 4).
Tab. 2
Specifications of selected earthquakes
|
Vs (m/s) |
Rjb (km) |
Fault type |
Magnitude |
Country |
Event |
|
466.12 |
9 |
Strike slip |
6 |
US |
Parkfield |
|
430.36 |
7.31 |
Strike slip |
6.46 |
US |
Big Bear |
|
471.53 |
15.19 |
Strike slip |
6.53 |
US |
Imperial Valley |
|
609 |
7.08 |
Strike slip |
6.9 |
Japan |
Kobe |
|
454.2 |
3.93 |
Strike slip |
7.14 |
Turkey |
Duzce |
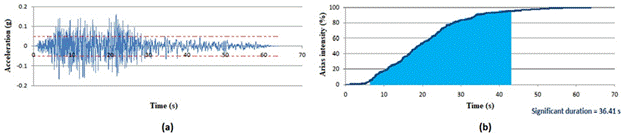
Fig. 4. Significant duration related to one of the
Imperial Valley earthquake components by the enclosed time method (a) and the
arias intensity method (b)
4. MODELLING
In order to evaluate the behaviour of
reinforced concrete box girder bridges equipped with fibre-reinforced
elastomeric bearings under near-field earthquakes, three isolated bridges with
different spans and identical characteristics, including similar materials,
sections, and dimensions were modelled. The bridges modelled had three
continuous 40 m (S40), 30 m (S30), and 20 m (S20) spans with the average height
of piers of 7.5 m, respectively (Figure 5). The deck cross-section selected for
the considered bridges had an area and moment of inertia of 10.42 m2
and 11.24 m4, respectively. Given the 16 m bridge width and the
assumption of a standard width of 3 m per lane, five lanes were considered for
bridges. In each bridge, eight seismic elastomeric bearing isolators reinforced
with fibre were exploited, so that in each support, including abutments and
bents, two bearings were used. The characteristics of the used bearings were
the same as the bearing introduced in the verification section. After modal
analysis of bridges, it was observed that the value of the fundamental period
of the bridge with a longer span was higher in comparison to the other bridges.
So that the first mode periods for the three S40, S30, and S20 bridges were
3.13, 2.65, and 2.17 s, respectively.
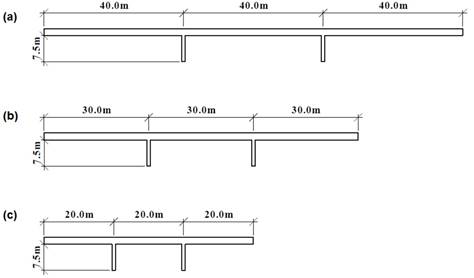
Fig. 5. Transverse view of the bridges S40 (a), S30
(b), and S20 (c)
5. RESULTS OF GRAVITATIONAL LOADING
OF BRIDGES
Generally,
in terms of loading, the bridge components are divided into two categories of
load-bearing and non-bearing components. Load-bearing components are elements
with a structural performance and non-bearing components include parts such as
cables, tubes, pavement asphalt, insulation, etc., [12]. According to Figure 6,
the traffic load was considered as a truck with a weight of 400 kN and a length
of 10 m, with the space of 3 m empty in the front and 3 m empty in the back. In
the rest of the passage line, a uniform load of 15 kN was placed. Moreover, the
load of the sidewalk was 2 kN/m. As shown in Figure 7, the maximum and minimum
envelope graphs resulting from the combination of dead loads and the truck
moving-load along different bridges were compared with each other. Noticeably,
the effect of increasing the span length on the moment applied to the bridges
is quite evident, so the higher the span length, the more moment applied to the
bridge deck.
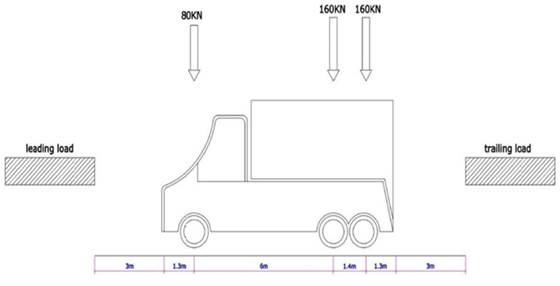
Fig. 6. Traffic load details [13]
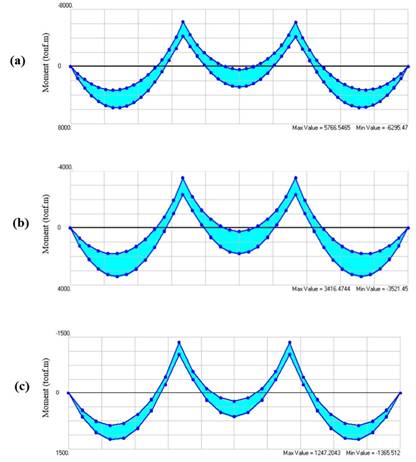
Fig. 7.
Results of the maximum and
minimum moments along
the longitudinal axis of the S40 (a), S30 (b), and S20 (c) bridges
6. RESULTS OF LATERAL LOADING OF
BRIDGES
The
components forming bridges are divided into two parts of the substructure and
superstructure. The main objective of using seismic bearings between the
substructure and superstructure was to reduce the transfer of the substructure
acceleration to the superstructure by absorbing the energy of strong movements
of the earth by the seismic bearings. In fact, the smaller the ratio of
acceleration of the superstructure to the substructure in the isolated bridges,
the better the performance of the seismic bearings. After comparing the
superstructure to substructure acceleration ratio of the bridges examined, it
was observed that the maximum superstructure acceleration had a lower value in
comparison to the maximum substructure acceleration for all cases, except for
one case involving the S40 Bridge under the Kobe earthquake (Table 3). The
difference between the values of the acceleration ratio in the bridges under
study can be attributed to the dependence of performance of the seismic
elastomeric bearing isolators reinforced with fibre on the frequency content of
the selected earthquakes. It should be noted that the unexpected rise in the
maximum superstructure to substructure acceleration ratio in the S40 structure
under the Kobe earthquake was observed only in one pulse in the acceleration
time history and, in overall, the bearing showed a suitable performance. Figure
8 illustrates a sample time history of the acceleration applied on the
substructure and superstructure under the influence of the Big Bear earthquake
on the S20 Bridge.
Tab. 3
Comparison
of the values of the maximum
superstructure to substructure acceleration ratio
|
Superstructure to substructure acceleration ratio
(%) |
Events |
||
|
S20 |
S30 |
S40 |
|
|
96.17 |
90.35 |
88.69 |
Parkfield |
|
62.81 |
61.87 |
61.30 |
Big Bear |
|
55.33 |
52.54 |
51.06 |
Imperial
Valley |
|
84.98 |
75.57 |
125.86 |
Kobe |
|
73.45 |
73.27 |
74.11 |
Duzce |
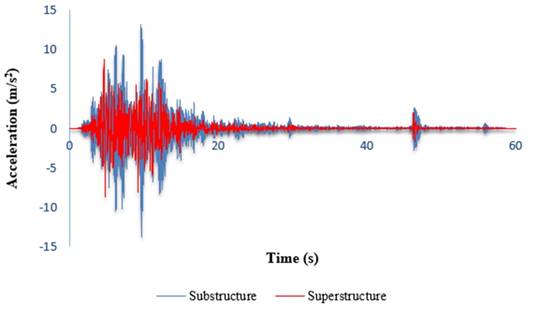
Fig. 8. Time history of the bridge superstructure
and substructure
accelerations under the Big Bear earthquake on the S20 Bridge
7. CONCLUSION
In
this study, the performance of three reinforced concrete box girder bridges
isolated with elastomeric bearings reinforced with fibre, which is a novel
issue in civil engineering, was investigated. Given the moment envelope
diagrams under gravity load, the bridge with a longer span, hence, with more
mass compared to the other two bridges, tolerated a higher moment. Due to the
continuity of the bridge deck, the maximum moment due to dead and traffic loads
occurred in the middle supports. In general, seismic isolation reduced the
superstructure to the substructure acceleration ratio, indicating the suitable
behaviour of the elastomeric bearing reinforced with fibres in considered
bridges. This acceleration reduction ranged from 4 to 50% under near-field
earthquakes, suggesting the dependence of the seismic elastomeric bearing
reinforced with fibres on the frequency content of the earthquake. The use of
this type of bearing in the industry as a substitute for other conventional
tools is still being discussed, while civil engineers presently regard this
type of bearing with conservative vision. Conclusively, to spread the
investigations in this area, the authors recommend generalising studies in the
future to other types of bridges and comparing the behavior of fibre bearings
with other conventional devices.
References
1.
Li Xinle, Hui Jiang, Dan Shen. 2012. ,,Study on seismic safety performance for
continuous girder bridge based on near-fault strong ground motions”. In 2012
International Symposium on Safety Science and Technology: 916-922.
Nanjing, China. ISBN 9781627486156. DOI:
https://doi.org/10.1016/j.proeng.2012.08.259.
2.
Housner George W., Donald E. Hudson. 1958. ,,The Port Hueneme earthquake
of March 18, 1957”. Bulletin of the
seismological society of America 48:
163-168. ISSN 0037-1106.
3.
Hall John F., Thomas H. Heaton, Marvin W. Halling, David J. Wald. 1995.
,,Near‐source ground motion and its effects on flexible buildings”.
Earthquake Spectra 11(4): 569-605. ISSN 8755-2930. DOI:
https://doi.org/10.1193/1.1585828.
4.
Liao Wen I., Chin Hsiung Loh, Shiuan Wan, Wen Yu Jean, Juin Fu Chai.
2000. ,,Dynamic responses of bridges subjected to near‐ fault ground
motions”. Journal of the Chinese Institute of Engineers 23(4):
455-464. DOI: https://doi.org/10.1080/02533839.2000.9670566.
5.
Hudson Donald E., George W. Housner. 1958. ,,An analysis of
strong-motion accelerometer data from the San Francisco earthquake of March 22,
1957”. Bulletin of the seismological
society of America 48: 253-268. ISSN
0037-1106.
6.
Bolt Bruce A. 1971. ,,The San Fernando, California earthquake of
February 9, 1971: Data on Seismic Hazards”. Bulletin of the seismological society of America 61: 501-510. ISSN 0037-1106.
7.
Bertero Vitelmo V., Stephen A. Mahin, Ricardo A. Herrera. 1978.
,,Aseismic design implications of near-fault San Fernando earthquake
records”. Earthquake Engineering and Structural Dynamics 6(1):
31-42. ISSN 1096-9845. DOI:
https://doi.org/10.1002/eqe.4290060105.
8.
Toopchi-Nezhad Hamid, Michael J. Tait, Robert G. Drysdale. 2008.
,,Testing and modeling of square carbon fiber-reinforced elastomeric seismic
isolators”. Structural Control and Health Monitoring 15: 876-900.
ISSN 1545-2263. DOI: https://doi.org/10.1002/stc.225.
9.
Kelly James M. 1997. Earthquake-resistant design with rubber. 2nd ed.
Springer-Verlag London. ISBN
978-1-4471-0971-6.
10.
Karimzadeh Naghshineh
Ali, Ugurhan Akyuz, Alp Caner. 2015. ,,Lateral response comparison of unbonded
elastomeric bearings reinforced with carbon fiber mesh and steel”. Journal
of Shock and Vibration, ISSN 1875-9203. DOI:
http://dx.doi.org/10.1155/2015/208045.
11.
Vatanshenas Ali, Davood Sharif Bajestany, Arian Aghelfard. 2018. Guidelines
to select and scale earthquake records for time history analysis of structures.
Salehian Publications. ISBN:
978-622-214-003-8.
12.
Iranian Standards No. 139. 2000. Standard Loads for Bridges.
Tehran: Office of the Deputy for Technical Affairs, Bureau of Technical Affairs
and Standards, Management and Planning Organization.
13.
Vatanshenas Ali, Davood Sharif Bajestany, Arian Aghelfard. 2018. ,,The
effect of seismic isolation on the response of bridges”. International Journal of Bridge Engineering (IJBE) 6(3): 61-74. ISSN 2241-7443.
Received 10.06.2019; accepted in revised form 29.08.2019
![]()
Scientific
Journal of Silesian University of Technology. Series Transport is licensed
under a Creative Commons Attribution 4.0 International License