Article
citation information:
Homišin, J. Static optimisation of
mechanical systems based on the method of extremal regulation. Scientific Journal of Silesian University of
Technology. Series Transport. 2019, 103,
15-29. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2019.103.2.
Jaroslav HOMIŠIN[1]
STATIC
OPTIMISATION OF MECHANICAL SYSTEMS BASED ON THE METHOD OF EXTREMAL REGULATION
Summary. A change in torsional stiffness of pneumatic tuners
can be achieved by changing the pressure of the gaseous medium in the course of the mechanical systems'
operation or while idle. Based on this statement, we tuned mechanical systems with torsional
vibration when they are either idle or when they reach stable condition during operation. The principle
of tuning mechanical systems with
torsional vibration during operation when their condition is stable lies
in the appropriate adaptation of basic dynamic properties (dynamic torsional
stiffness and damping factor) of the pneumatic tuner to the dynamics of the
system. This was achieved with a control system that helps create a closed
control feedback loop. In this way, we can continuously change, that is, adapt
the dynamic properties of the pneumatic tuner to the dynamics of the mechanical
system so that no dangerous torsional vibrations occur while the system is in
operation mode.
Keywords: static optimisation of
mechanical systems, method of extremal regulation, continuous tuning of
mechanical systems
1. INTRODUCTION
Change
in the torsional stiffness of pneumatic tuners can be achieved by changing the
pressure of the gaseous medium, either in the course of operation or when the
mechanical systems are idle. This implies the two proposed ways of tuning
mechanical systems with torsional vibration (MSTV):
o
tuning mechanical systems with torsional
vibration when idle, thus ensuring the condition of tuning the said systems.
o tuning
mechanical systems with torsional vibration during operation when they are in
stable condition, thus ensuring the condition of continuous
tuning of the said systems.
The principle of tuning
the mechanical systems during operation when their condition is stable lies in
the appropriate adjustment of the pneumatic tuner’s basic dynamic
properties (dynamic torsional stiffness and damping coefficient) to the
dynamics of the system. This is ensured with a control system that helps create
a closed control feedback loop. In this way, we can continuously change, that
is, adapt the dynamic properties of the pneumatic tuner to the dynamics of the
mechanical system so that no dangerous torsional vibration occurs during the
system operation mode.
The proposed methods of
tuning mechanical systems are possible to apply due to the control circuits and
control systems, for which the author has been granted patent protection[2], and they can be
implemented as follows:
· via a control system
that ensures a continuous change in the characteristics of the pneumatic
couplings.
· by means of a control
system that enables a continuous tuning of the mechanical system.
· by applying a pneumatic
coupling with an additional control system.
· through static optimisation based on the method
of extremal regulation.
· by using a
self-regulating pneumatic coupling.
2. BASIC PRINCIPLE AND FOUNDATION
OF STATIC OPTIMISATION OF MECHANICAL SYSTEMS BASED ON THE METHOD OF EXTREMAL
REGULATION
As already mentioned,
dangerous torsional vibration is very common in mechanical systems driven by
pistons, acting in the role of either the driving or the driven aggregates.
Intense torsional vibration causes excessive dynamic stress to the entire
machine. For this reason, a justified need exists to control dangerous
torsional vibration in these mechanical systems and the mechanical jitter
generated thereby. Currently, this problem is solved by the appropriate
adaptation of dynamic properties of the flexible shaft coupling to the dynamics
of the system. This means that the mechanical system must be suitably
dynamically tuned in advance to the main harmonic componet of the piston
machine.
The aim is to achieve
the right resonance from the main harmonic component, that is, the critical
speed exists at a sufficient distance from the working speed range of the
machine in question.
However, the present
tuning method will only be suitable if there are no unforeseen (accidental)
failure effects during the system's operating mode. That is, if there is no
mechanical failure, especially of the piston machine.
In the event of failure
of the piston machine [1], [2], [3], [4], [5], [6] highly intense resonance of
components with minor – lower harmonic excitation occurs in the operating
mode, resulting in critical speed.
It can be deduced from
the dynamic point of view that it is possible to characterise the MSTV as
systems most often operating in the supercritical region with relatively fast
transition upon their start up and shut down. In terms of control, however,
they belong to a group of controlled systems with incomplete information.
Incompleteness of information is manifested mainly in the area of unforeseen
failure effects, that is, in the area of accidental failures.
Drawing on the MSTV
characteristics, as well as on the advantages and disadvantages of the current
solution to the given problem in the area of dangerous torsional vibration [7],
[8], we proposed to control the torsional vibration and the mechanical
vibration generated thereby through static optimisation (direct optimisation) based on the method of extremal regulation during stable operating condition.
Our main criterion for optimising any MSTV is to
achieve minimum torsional vibration values and minimal mechanical vibration
generated consequently.
In this respect, it
should be noted that the static optimisation
of MSTV by the method of extremal regulation is currently, not being
practically implemented at all. This is mainly due to the fact that basic
conditions have not yet been established for the possible implementation of
this method. However, the existence of a pneumatic torsional vibration tuner, that is, an element that is able
to change its basic characteristics during operation, in particular, its
dynamic torsional stiffness, provides all the prerequisites for enabling
extremal regulation in MSTV.
Implementing static optimisation in MSTV requires the
following conditions be met:
v
MSTV must meet the basic requirements for continuous tuning, that is,
tuning the system while it is running in a stable condition.
v
It is not necessary to know the mathematical model controlling the MSTV
to carry out their static optimisation.
Nevertheless, it is necessary to know whether the purpose function of the system (function of input and output
variables) has an extreme [9], [10],
[11], [12], [13], [14], [15], [16].
2.1. Characteristics and
execution of continuous tuning of mechanical systems with torsional vibration
Drawing on the nature of
the patents[3], it is clear that the
system at hand must include a pneumatic torsional tuner[4] regulated by the
control system[5] of Fig.1.
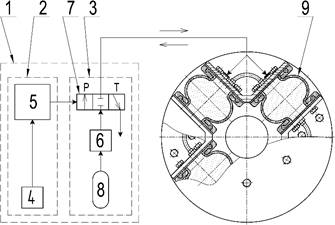
Fig.
1.
Schematic representation of the regulation of continuous change in the characteristics
of the pneumatic tuner by means of a control system.
Fig.1 is a schematic representation of
the control system and a schematic representation of how the pneumatic
torsional tuner is controlled.
The control system (1)
consists of a controlling (2) and an actuating subsystem (3). The
controlling subsystem (2) features a
microprocessor (5) and a piezoelectric sensor of mechanical vibration
acceleration (4). The sensor (4), located on the mechanical
system, sends an electrical signal to the microprocessor (5),
proportional to the system's mechanical vibration. The actuating subsystem (3)
consists of an electromagnetic switchboard (7), which is connected to
the gaseous medium reservoir (8) via a control valve (6). By
switching the two-position electromagnetic switchboard (7), the
microprocessor (5), which constitutes the basic control component of the
entire control system (1), causes it to move, thereby increasing or
decreasing the pressure of the gaseous medium in the compressive space of the
pneumatic torsional vibration tuner through the supply circuit P or
discharge circuit T.
When the mechanical
system operates in an unfavourable operating mode, the whole system starts
jittering due to the magnitude of torsional vibration, the acceleration of which
is measured by a mechanical vibration sensor (4). After the
microprocessor (5) receives and evaluates the electrical signal
proportional to the system's mechanical jitter, the switchboard (7) is
switched to the supply position P or a discharge position T. As a
result, the pressure of the gaseous medium in the pneumatic elastic elements (9)
of the pneumatic tuner's compression space changes, which represents a
continuous change in its basic dynamic properties, that is, dynamic torsional
stiffness, while the mechanical system is running.
The result of the
operation of the control system is that, due to a continuous change in the
pressure of the gaseous medium in the pneumatic tuner, a change in its basic
dynamic property, that is, dynamic torsional stiffness is achieved. By changing
the dynamic torsional stiffness, the intrinsic frequency of the system changes,
thus, adapting to the frequency of the i-th harmonic component of the load
torque so that the system does not operate in resonance with any torque excitation
component, that is, until the following condition is met:
![]() (1)
(1)
2.2 The trend of the special purpose
function of the implemented mechanical system with
torsional vibration
As part of the basic requirements set out, in the static optimisation of MSTV implemented through the application of extremal regulation, it
is necessary to know in advance whether the trend of the system's special
purpose function will have an absolute or a relative minimum in the set
operating mode. With respect to the above requirement, the trend of the special
purpose function at the implemented MSTV was to be identified and verified. The
trends of the special purpose function were established theoretically, that is,
by calculation, based on the theoretical model and practically, on the basis of
experimental measurements performed.
2.2.1 Special purpose function's trends
established by calculation
The calculated trends of the MSTV special
purpose function are shown in Fig. 2a,
b, c. They represent the resonance curve of the twist angle φd of the pneumatic tuner
dependent on the pressure of the gaseous medium ps inside of it. The twist angle φd ,
expressed by relation (2),
characterises the output, that
is, the controlled quantity, and
the pressure of the gaseous medium ps, the input, that is ps say, the action causing
variable.
![]() (2)
(2)
The amplitude value of the
harmonic component of the twist angle, expressed by (3), mostly depends on the frequency ratio of the i-th
harmonic component of the load torque and the intrinsic frequency of the system
(![]()
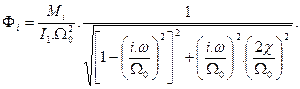 (3)
(3)
The intrinsic frequency ![]() is influenced by
the dynamic torsional stiffness, which according to (4), is a function of the
pressure of the gaseous medium ps in the pneumatic tuner.
is influenced by
the dynamic torsional stiffness, which according to (4), is a function of the
pressure of the gaseous medium ps in the pneumatic tuner.
![]() (4)
(4)
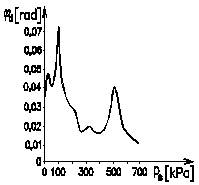
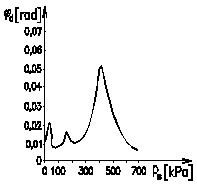
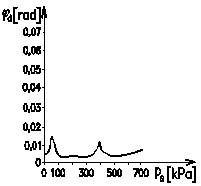
a)
b) c)
Fig. 2. The trends of the special
purpose functions of the dynamic twist angle φd dependent on the pressure of ps gaseous medium ps in the pneumatic
torsional tuner.
The trends of the
special purpose function were construed at constant excitation speed n =
400 min-1 (Fig.
2a), n = 760 min-1 (Fig. 2b) and n = 1100 min-1 (Fig. 2c) with a simulated fault
variable characterised by uneven excitation of the individual compressor
cylinders. In the present case, it was understood that the first and third
cylinders operate at 15%
greater power and the second cylinder at 15%
less than the average power per cylinder.
Based
on the above-mentioned trends of the special purpose function of the modelled
MSTV, it can be stated that they have clear relative minimums.
2.2.2 Trends of the special purpose
function of the system established experimentally
Practical measurements were made on the mechanical system implemented as
per Fig. 3. The trends of the
dynamic load torque component were measured by a torque sensor (8) and
simultaneously, the jitter generated in the mechanical system was measured by a
piezoelectric sensor (12).
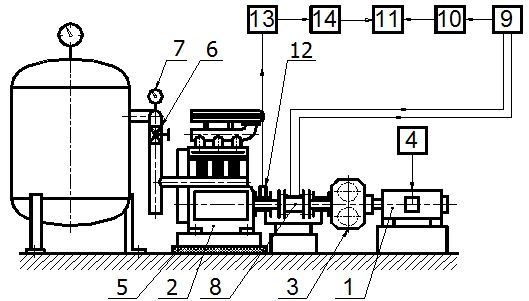
Fig.
3.
Implemented mechanical system with schematic interconnection of the measuring
apparatus applied.
The measurements were
made assuming balanced excitation of the individual compressor cylinders at a
constant speed of n = 760 min -1. The pressure of the gaseous
medium in the pneumatic tuner was changed during the measurements to the extent
of ps = 0 ÷ 700 kPa with a change after 100
kPa.
After amplification by
the amplifier (9) and filtering by the band frequency filter (10),
the electrical signal from the torque sensor (8) was recorded by a
measuring tape recorder (11). Similarly, the electrical signal from the
piezoelectric sensor (12), located on the torque sensor bearing housing,
was simultaneously recorded by the tape recorder (11) after
amplification by the amplifier (13) and the band frequency filter (14).
The recorded signals
were further processed by a narrowband spectral analyzer, with the output in
the form of the frequency spectrum characteristic trends of the AM
dynamic load torque component (Fig. 4)
and the jitter amplitudes of the ACH system (Fig. 5).
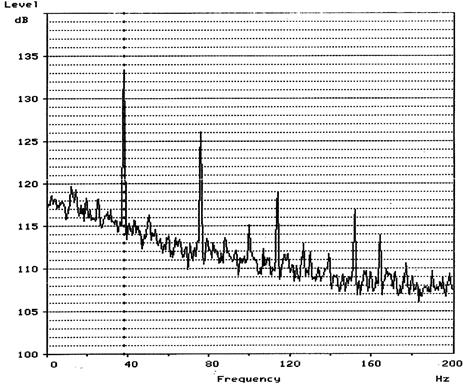
Fig.
4.
Frequency spectrum characteristic of torque load AM when
applying a pneumatic tuner with gaseous medium pressure ps = 400 kPa.
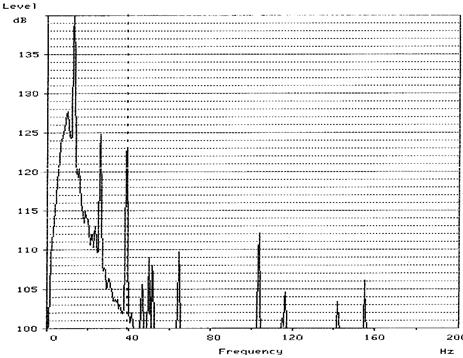
Fig.
5. Frequency
spectrum characteristics of the ACH amplitudę jitter
when applying the pneumatic tuner with the gaseous medium pressure of ps
=
400 kPa.
From the results of the practical measurements, it is clear that the
most significant amplitudes were at the first, second and third harmonic
components of the speed frequency. Since the amplitudes of the first and second
harmonic components were influenced by the imbalance of the rotating parts and
the misalignment of the shafts of the given system, the evaluation will show
the results of
the frequency spectrum characteristics of the torque amplitude AM
(Fig. 4) and the mechanical jitter of the ACH system (Fig.
5) shall relate to the amplitude of the third
harmonic component. The reason behind this is the fact that the third harmonic
component of the rotational frequency manifests itself mainly by the action of
the torsional vibration generated in the mechanical system (by the action of
the excitation device, in our case the compressor).
Amplitude curves of the load torque's dynamic component AM were processed from the frequency spectrum characteristics obtained (Fig. 6) and from the ACH jitter amplitude (Fig. 7) dependent on the pressure of
the gaseous medium in the pneumatic tuner.
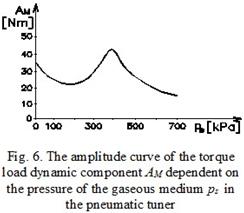
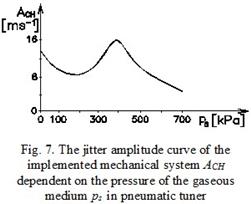
The trend of Fig. 6 or Fig. 7 is understood to be the
trend of the output variable AM or
ACH,
dependent on the input variable ps, hence, as a special purpose function of
the implemented MSTV. The figure shows that the dependence of AM =
f(pS) and ACH
= f(pS) has its minimum extreme in the range of the
gaseous medium pressures between ps = 200 kPa and 700 kPa.
2.2.2. Control circuit and control
algorithm to ensure static optimisation of mechanical systems with torsional vibration
Static optimisation of MSTV can be achieved by the method of extremal
regulation by step change in the action variable according to the control
circuit as shown in Fig. 8[6].
The control circuit (Fig. 8) consists
of a controlled MSTV (1), a piezoelectric sensor of mechanical jitter (2),
which sends an electrical signal to an extremal controller (4),
proportional to the mechanical jitter of the ACH. Through
built-in control algorithm (Fig. 9), the extremal regulator processes the
electrical
signal and with the aim to search for the minimum extreme, it controls the
actuator (5), characterised in Fig.
1, through a two-position electromagnetic switchboard (7). By
controlling the actuator, we regulate the action variable ps, that is, by supplying the gaseous
medium or by discharging it, we increase or reduce the pressure in the
pneumatic tuner.
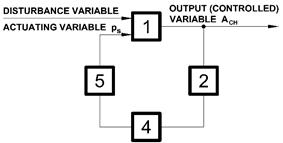
Fig. 8.
A control circuit to ensure extremal control in a mechanical system with
torsional vibration.
It is obvious from the
control algorithm (Fig. 9) that after determining the time between two
consecutive measurements ∆t and after determining the bandwidth of
the controlled variable u deadband, either the first value
of torsional vibration AT (ti–1) or of
mechanical jitter ACH (ti–1) is measured. After
measuring another AT (ti) or ACH (ti ) value,
the static optimisation of the MSTV, controlled by the
extremal regulation, will comply with the said algorithm.
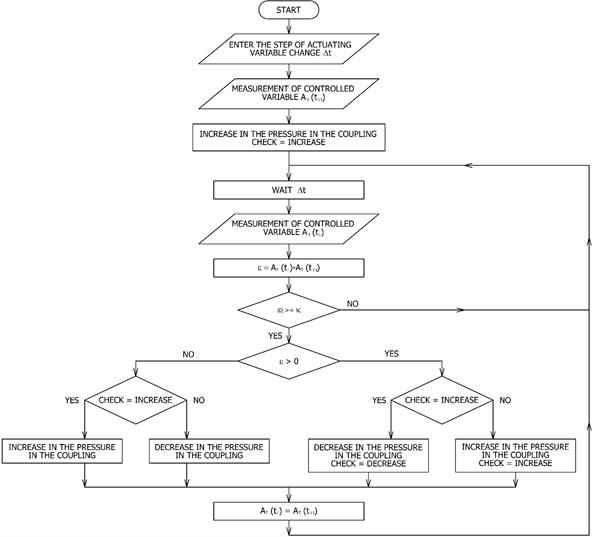
Fig. 9.
Algorithm controlling the extremal regulation.
3. results of the application of extremal
regulation to the implemented mechanical system WITH TORSIONAL VIBRATION
Fig.
10 shows
the dynamic tuning of the implemented mechanical system by pneumatic torsional
vibration tuner, via the amplitude curves of the dynamic components of the
twist angle of the pneumatic tuner dependent on the speed (a, b, c). At
the same time, the figure also shows the influence of the secondary harmonic
components on the magnitude of the torsional vibration of the mechanical
system, which is presented as dynamic characteristics trends b, c.
Trend a shows the
dynamic characteristic in case of a trouble-free operation of the piston
machine. The failure rate of the piston machine is shown as characteristics of
the trend b, c. The trend b characterises the failure of
uneven excitation of the individual cylinders of the piston machine (in the
range ± of 15%), while the trend c is characterised by the failure of one
cylinder that ceased to operate. The individual trends are processed in the
above figure with the pressure of the gaseous medium in the pneumatic tuner
being ps = 700 kPa.
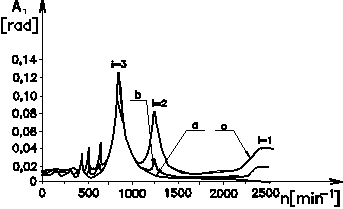
Fig. 10. Amplitude
curves of dynamic components of the twist angle φd of the pneumatic tuner dependent on the speed n.
Fig.10 shows that the
condition of removing the critical speed to a sufficient distance from the
operating speed range is met by the trends of all characteristics. This means
that MSTV has been suitably dynamically tuned in advance to the main harmonic
component (i = 3) of the torque load.
Within the operating
speed range (n =1000 ÷ 2500 min-1), the dynamic
characteristic is of decreasing nature and the magnitude of torsional
vibration, characterised by a dynamic twist angle, ranges from φd = 0,65° ÷
0,25°. This is due to the fact that, in case of trouble-free operation of the
piston machine, the secondary harmonic components (i=1 and 2) have a very low
torsional excitation potential. Their potential increases if failure of the
piston machine occurs (characteristics b, c). In the event of uneven
excitation of the individual compressor cylinders, at the critical speed
locations for i = 2 , the magnitude of the torsional vibration increases
almost 13-fold compared to the
failure-free operation of the piston machine, which represents
the dynamic twist angle φd = 1,15° (φd = 0,7° for i=1),
while in the case one cylinder is out of order, it reaches up to 60-fold value, which causes an
increase in the dynamic twist angle to φd =4,1° (φd = 3° for i=1).
The momentary reduction
of dynamic load by controlling the torsional vibration would be of great
importance for each MSTV in such cases.
The presentation of how
torsional vibration was controlled, as well as mechanical jitter of the system
at hand by static optimisation
based on the method of extremal
regulation was performed under the following conditions:
· during stable operating
mode of a given system, that is, at constant operating speed in the range of n
= 1000 ÷ 2500 min-1 characterised in Fig. 11 and Fig. 12 in positions (1) to
(10).
· provided the piston
machine fails when one cylinder stops working.
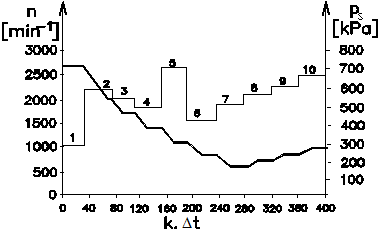
Fig.
11. The
result of the static optimisation of the implemented system, characterised by
the change in the value of the action variable pS at the speed range n, dependent on the discrete time
k.Dt.
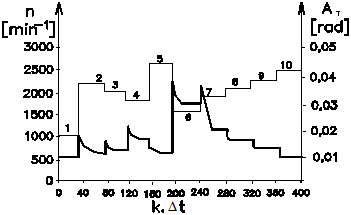
Fig.
12. The
result of the static optimisation of the implemented system, characterised by a
change in the value of the controlled variable AT, at the operating speed range
n, dependent on the discrete time k.Dt.
The results of the
static optimisation are achieved by controlling the pressure of the gaseous
medium ps in the pneumatic tuner (Fig.11) and then regulating the
torsional vibration magnitude of the AT system (Fig.12),
that is, by stabilising it, particularly, in ten random operating modes. Given
that this is a simulation of extremal regulation, any change in the working
mode, that is, the operating speed is in this case at hand done by a jump.
Let us assume the MSTV
operates, for example, in the fifth operating mode, characterised by the speed n5
= 2500 min-1. In this case, the pressure of the gaseous
medium in the pneumatic tuner stabilised at pS5 = 278 kPa
and in terms of torsional vibration, the system is stabilised when the value of
AT5 = 0,01 rad (0,57°). By changing the operating
mode from n5 = 2500 min-1 to n6 =
1400 min-1, the magnitude of torsional vibration increases from AT5
= 0,01 rad to AT6 = 0,03 rad (2°).
Through monitoring the given system, the optoelectronic sensor sends an
electrical signal to the extremal controller. Based on the results of the
control algorithm (Fig. 9) of
the extremal regulator, the pressure of the gaseous medium is reduced from
pS5 =278 kPa to the stable value of pS6*=219
kPa. By varying the overpressure of the gaseous medium, the dynamic
torsional stiffness of the pneumatic
tuner kd,
is regulated, resulting in a change in the system's inherent frequency![]() . The amplitude value of the dynamic component of the pneumatic tuner
twist angle according to (2)
depends basically on the frequency ratio of
the i - th harmonic component of the torque load and the
intrinsic frequency of the system (iw/W0). This means that the
magnitude of the torsional vibration of the mechanical system AT, characterised by the dynamic component of the twist angle, will
depend on the change in the pressure of the gaseous medium in the compressor
space of the tuner.
. The amplitude value of the dynamic component of the pneumatic tuner
twist angle according to (2)
depends basically on the frequency ratio of
the i - th harmonic component of the torque load and the
intrinsic frequency of the system (iw/W0). This means that the
magnitude of the torsional vibration of the mechanical system AT, characterised by the dynamic component of the twist angle, will
depend on the change in the pressure of the gaseous medium in the compressor
space of the tuner.
In this particular case,
the reduction of the pressure of the gaseous medium (pS5 to pS6*)
as an action variable causes a reduction in the magnitude of the torsional vibration,
that is to say, the controlled quantity from the AT6 = 0,035 rad to the stable value of AT6*=
0,025 rad (1,4°).
It can be inferred from
the above that in the sixth operating mode, in terms of torsional vibration
magnitude, the MSTV stabilised at the value of AT6* = 0,025 rad.
Since the parameters of
regulating the system's dynamic characteristics are not yet known (they are
currently being established in experimental measurements), the values (n, pS , AT) are shown in Fig. 11 and Fig. 12, respectively, depending on the discrete time k.Dt for 400 simulation steps.
4. CONCLUSION
Among other things, the results of this paper confirm that dangerous
torsional vibration of any mechanical system can be reduced to an acceptable
level by suitably adapting the dynamic properties of the pneumatic torsional
tuners. This means that mechanical systems with torsional vibrations need to be
pre-tuned or tuned in advance. In order to tune the mechanical systems with
torsional vibrations, it is necessary to do a detailed dynamic calculation in
terms of torsional vibration. If powerful turbocharged diesel engines are used
in mechanical systems, the dynamic calculation is not sufficient only for
balanced excitation of the individual engine cylinders. It must be borne in
mind that during a system operation mode, unforeseen (accidental) fault effects
may occur, most often characterised by a failure of the piston device itself.
The excitation of individual cylinders of the diesel engine is practically
uneven, and at the same time, a cylinder that stops working is a very frequent
failure effect of the piston device. As a result of this, there is a clear
increase in torsional vibration of the mechanical system and the entire device
jitters. This causes increased dynamic stress on the individual parts of the
mechanical system and, in particular, of the flexible shaft coupling, as being
relatively the weakest part of the mechanism.
Reining in dangerous torsional vibration of mechanical systems operating
with a wide range of revolutions is currently done by using very flexible
couplings with appropriately chosen nonlinear characteristics. Only some types
of flexible couplings are able to meet this requirement because not all types
of couplings enable reaching sufficiently low torsional stiffness while
maintaining sufficiently suitable strength properties. The torsional stiffness
and strength properties depend on the shape of the elastic element and the
material from which the elastic element was made. At the same time, it should
be noted that any linear or non-linear flexible coupling currently used has
only one characteristic. This fact then translates into only one trend of its
inherent speed frequencies in the Campbell diagram. To change the
characteristics of the flexible coupling to fit its dynamic properties with the
dynamics of the system means to use another element of the flexible coupling or
to use another flexible shaft coupling. In any case, fatigue and ageing of
elastic materials cannot be overlooked, which ultimately greatly affect the
original dynamic properties of the coupling. Thus, the transience of dynamic
properties of elastic couplings caused by ageing and fatigue of their elastic
elements, as well as the frequent failure of some other members of the system, causes
the pre-tuned mechanical system with torsional vibration to misalign. In such a
case, its tuning member, that is, the flexible shaft coupling is in no position
to eliminate or reduce increasingly dangerous torsional vibration.
In view of the above and with the aim of tuning the
mechanical systems with torsional vibration to limit dangerous torsional
vibration, we have proposed using the pneumatic torsional tuners developed by
us. These pneumatic tuners do not have one, but a whole range
of characteristics, as well as a range of the typical ones. The properties of
these tuners are mainly influenced by the change in the pressure of the gaseous
medium in its compression space.
Based on the results of the
experimental verification, we noted that by changing the pressure of the
gaseous medium in the compressor space of the pneumatic tuner, change in its
dynamic torsional stiffness was achieved, which had a decisive influence on the
system's inherent frequency. The essence of the principle of tuning mechanical
systems with torsional vibration with pneumatic tuners lies in the adaptation
of the intrinsic angular frequency of the mechanical system to the excitation
angular frequency, so no resonance condition emerges during the system's
operating mode and consequently, no dangerous torsional vibrations occur.
Based on the results of the analysis of balanced excitation, uneven
excitation of individual engine cylinders and the failure of one cylinder,
which stopped working, it can be stated that the introduced pneumatic tuner has
met all the requirements for its application in mechanical systems with
torsional vibration with constant operating speed and operating speed range. At
the same time, it was also confirmed that it is possible to reduce the
unfavourable consequences of unforeseen breakdown effects occurring in
mechanical systems by optimising the mechanical systems with torsional vibration as
proposed. The optimisation in question is a static optimisation of the
mentioned system during operation in a stable condition, which we proposed to
ensure that by using the method of extremal regulation through the step change
in the action variable. The results of the simulation confirmed that the static
optimisation of the mechanical systems by using the indicated method translates
into reduction in dangerous torsional vibration in any mechanical system with
torsional vibration.
Finally, it can be argued that the proposed manner of tuning (continuous system
tuning) in operation can be applied wherever the need to prevent dangerous
torsional vibrations of mechanical systems exists. The presented results
confirm that these tuning methods can contribute to increasing the technical
level and operational reliability of all mechanical systems with torsional
vibration into which they are incorporated.
Acknowledgements
This paper was written within the framework of the Grant project VEGA
1/0473/17 “Research and development of technology for homogeneous charge
self-ignition using compression in order to increase engine efficiency and to
reduce vehicle emissions.“
References
1.
Böhmer Jürgen. 1983. „Einsatz elastisher
Vulkan-Kupplunen mit linearer und progressiver Drehfedercharakteristik”.
[In German: „Use of elastic volcano couplings with linear and progressive
torsion spring characteristics”]. Motortechnische Zeitschrift 44(5): 21-24.
2.
Lunke Martin, Beeftink g. Bernd.
1983. „Einsatz hochelastischen Kupplungen in energiesparenden
Schiffsantriebsanlangen”. [In German: „Use of highly flexible
couplings in energy-saving marine propulsion systems”]. Schiff und Hafen 4(35): 23-32.
3.
Zoul Václav.
1982. „Některá hlediska vývoje pružných
spojek pro soustrojí s naftovými motory”. [In Czech: „Some
aspects of development of flexible couplings for diesel engines”]. Strojírenství
32(6/7): 21-28.
4.
Lacko Pavol, Vladimír
Lacko. 2000. „Continuously driven rezonance”. Strojárstvo 42(3/4): 127-135.
5.
Zoul V., P.
Utěkal. 1978. „Výskum vlastností nelineárni
pružné spojky”. [In Slovak: „Research of properties of nonlinear
flexible coupler”]. Strojírenství
28(5): 25-34.
6.
Ubartas M., V. Ostaševičius, S. Samper, V. Jūrėnas,
R. Daukševičius. 2011. „Experimental investigation of
vibrational drilling”. Mechanika
4: 368-373.
7.
Kubík S. 1982. Teorie
automatického řízení II. (Optimální,
adaptivní a učíci se systémy). [In Czech: Theory of Automatic Control II. (Optimal,
Adaptive, and Learning Systems)]. Praha:
SNTL.
8.
Rastrigin A.A. 1974. Sistemy extremaľnogo upravlenija. [In Rusian: Extreme management systems]. Moscow: FML.
9.
Pešík L., Němeček P. 1997. Identification of the dynamic system of a machine with an elastic base.
McNU 97, Chicago, USA.
10.
Yubao S., W. Jihong, Y. Dianlong, W. Xisen. 2013. „Analysis and
enhancement of torsional vibration stopbands in a periodic shaft system”.
Journal
of Physics D: Applied Physics No 46
145306: 7-13. ISSN 0022-3727.
11.
James D. Van de Ven, J. Cusack. 2014. „Synthesis and baseline
testing of a digital pulse-width-modulated clutch”. Mechanism and
Machine Theory 78: 81-91. ISSN 0094114X.
12.
Mehlan A. 1996. „Hochelestische Kupplungen”. [In German:
„Highly elastic couplings”]. Antriebstechnik 35(11): 27-33.
13. Sága M., L.
Jakubovičová. 2014. „Computational analysis of contact stress
distribution in the case of mutual stewing of roller bearing rings”. Novel Trends in Production Devices and
Systems, Applied Mechanics and Materials 474: 363-368.
14.
Czech P. 2011. „Diagnosing of disturbances in the ignition system
by vibroacoustic signals and radial basis function - preliminary
research”. Communications in
Computer and Information Science 239: 110-117. 11th International
Conference on Transport Systems Telematics (TST 2011). Katowice-Ustron, Poland,
October 19-22, 2011. Modern Transport
Telematics. DOI: https://doi.org/10.1007/978-3-642-24660-9_13.
15. Ostaševičius
V., I. Milašauskaitė, R. Daukševičius, V.
Baltrušaitis, V. Grigaliūnas, I. Prosyčevas. 2010.
„Experimental characterization of material structure of piezoelectric
PVDF polimer”. Mechanika 6:
78-82.
16. Leskova Andrea, Hubert
Jurjewicz, Patrik Lenghart, Peter Bacik. 2018. “Current challenges of
digital technologies”. Komunikacie
1a. ISSN: 1335-4205.
Received 21.02.2019; accepted in revised form 19.05.2019
![]()
Scientific
Journal of Silesian University of Technology. Series Transport is licensed
under a Creative Commons Attribution 4.0 International License