Article
citation information:
Jírová, R., Svoboda,
R., Pešík, L. Seat suspension system of the electric golf cart. Scientific Journal of Silesian University of
Technology. Series Transport. 2018, 99,
89-94.
ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2018.99.8.
Radka JÍROVÁ[1],
Roman SVOBODA[2], Lubomír
PEŠÍK[3]
SEAT SUSPENSION
SYSTEM OF THE ELECTRIC GOLF CART
Summary. The paper deals with reducing vibrations transmitted
from electric golf cart wheels to the seat and the seated person. These vibrations
appear while driving a golf cart on uneven terrain of a golf course. This
problem can be solved by using the elastic and damping link between the cart
frame and seat, which is tightly connected to the electric power battery. A
mathematical calculation is used to evaluate the designed solution in which the
golf cart is defined as a system of masses connected with elastic and damping
links. The result of the designed solution’s mathematical description
provides a reference step response of the golf cart seat.
Keywords: suspension system; golf
cart seat; minimization of vibration
1. INTRODUCTION
Suspension
seats are used in a wide range of vehicles, especially for the purpose of
protecting people’s health when exposed to whole-body vibration during
travel, and also increasing comfort. Driving on the uneven terrain of a golf
course leads to the high-intensity vibration of wheels, which is transmitted to
the frame, the seat and the seated person. As conventional battery-powered
electric golf carts do not have suspension seats, the elastic and damping link
between the chassis and frame is used to reduce transmitted vibrations to the
seat and the seated person. Such a link only partially reduces the transmission
of vibrations, meaning that driving in a golf cart can still become
uncomfortable.
2. EFFECT OF VIBRATION ON COMFORT
Evaluating the effect of
vibration on the comfort of the seated person while driving a golf cart was
made in accordance with [1]. The result of this evaluation relates to the frequency‑weighted
root mean squared (RMS) acceleration of the measured acceleration as a function
of time during the golf cart drive; see the comparison with this acceleration
value in the table in [2]. A comparison of the frequency-weighted RMS
acceleration with the table in [1] shows that the effect of vibration on
comfort during golf cart driving is in interval between uncomfortable and very
uncomfortable [3].
3. REDUCTION OF
TRANSMITTED VIBRATION
Minimization of
vibration, transmitted from golf cart wheels to the seat and the seated person,
is based on the principle described in the patent application.
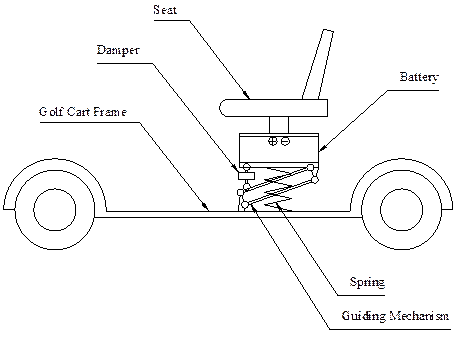
Fig. 2. Principle of vibration isolation of the
seat
Transmitted vibrations can be reduced by
using the elastic and damping link between the cart frame and seat, which is
tightly connected to the electric power battery. As a result of this tightness,
the seat increases the inertial effect of mass, which reduces seat vibration.
The principle is shown in Fig. 2.
4. TRANSMITTED VIBRATION
CALCULATION
The
system shown in Fig. 2 can be described in a simplified way by differential
equations:
(1)
(2)
where 
is the
mass of the frame, 
is the
mass of the seat, battery and seated persons, 
is the
damping coefficient of the chassis, 
is the
damping coefficient between the seat with the battery and the frame, 
is the stiffness of the chassis, 
is the
stiffness between the seat with the battery and the frame, 
is the
deflection of the chassis, 
is the
deflection of the frame, and 
is the
deflection of the seat with the battery.
The system can be
presented in a simplified matrix form by the following equation:
(3)
where 
is the vector of
deflection, 
is the
matrix of stiffness, 
is the
matrix of damping, 
is the
matrix of mass, 
is the
vector of the force substituting deflection 
, 
is the
angular frequency and 
is the
imaginary unit.
In the case of using an
elastic and damping link between the golf cart frame with a tightly connected
battery and the seat, the differential equations are:
(4)
(5)
where 
is the
mass of the seat and seated persons, 
is the
damping coefficient between the seat and the frame, 
is the stiffness between the seat and the frame,
and 
is the
deflection of the seat.
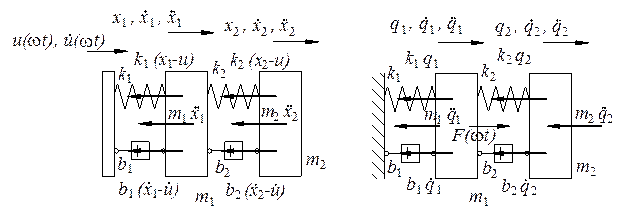
Fig. 3. Description of Eqs. 1-5
The results obtained by
Eqs. 1-5 comprise the amplitude-frequency response, as shown in
Fig. 4, and the reference step response of systems, as shown in
Fig. 5.
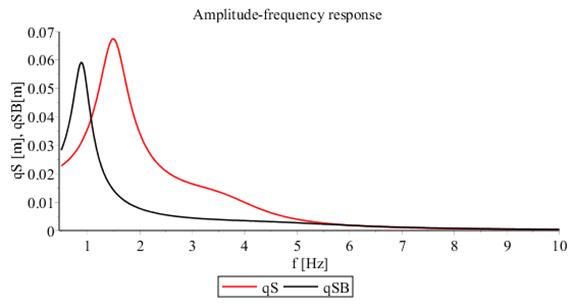
Fig. 4. Amplitude-frequency response
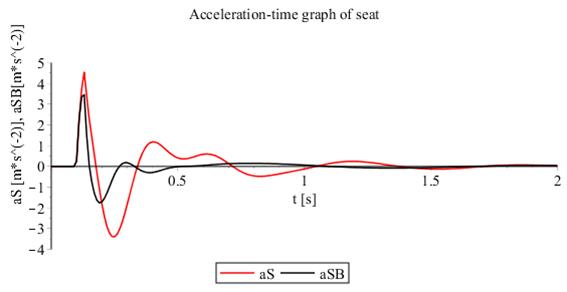
Fig. 5. Step response of systems: acceleration-time graph
Driving a golf cart on
uneven terrain of a golf course leads to non-periodic and non-harmonic
vibration. In a simplified way, this vibration can be represented by separate
step functions. The deflection in
differential Eqs. 1-5 can be substituted by a reference step signal. The
amplitude-frequency response, as shown in Fig. 4, is the decisive
reference step response of a system when evaluating the effect from increasing
seat inertia.
5. TRANSMITTED VIBRATION EVALUATION
The system of an electric golf cart
without a suspension seat can be described in a simplified way by the following
differential equation:
(6)
where 
is the
deflection of the frame with a seat.
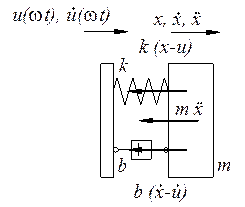
Fig. 6. Description of Eq. 6
The result obtained from
differential Eqs. 1-6 is the reference step response of systems. The
acceleration-time graph for the suspension seat and the seat tightly connected
to the golf cart frame is shown in Fig. 7.
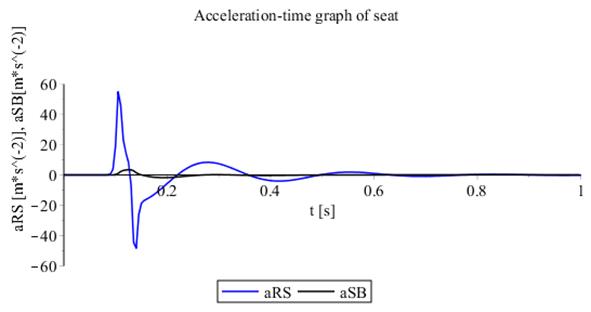
Fig. 7. Step response of systems: acceleration-time graph
6. CONCLUSION
The paper deals with the current
issue of the vibration isolation of golf cart seats. The solution uses the
inventive concept of increasing the inertia of the tightly connected mass in
relation to seat. This significantly reduces the vibration transmitted from the
golf cart wheels to the driver and passenger.
References
1.
ČSN ISO 2631-1. Vibrace a
rázy - Hodnocení expozice člověka celkovým
vibracím - Část 1: Všeobecné požadavky.
Prague: Český normalizační institut, 1999. [In Czech: Vibration and shock - Assessment of human
exposure to total vibration - Part 1: General requirements. Prague: Czech
Standards Institute, 1999.]
2.
Dresig Hans, Franz Holyweißig. 2008. Maschinendynamik. [In German: Machine
Dynamics]. Berlin: SpringerVerlag.
3.
Sapietova A., V. Dekys. 2016. „Use
od Msc. Adams software product in modeling vibration sources”. Komunikacie 1a (101): 101-107.
Received 02.03.2018; accepted in revised form 17.05.2018
Scientific
Journal of Silesian University of Technology. Series Transport is licensed
under a Creative Commons Attribution 4.0 International License