Article
citation information:
Ilewicz, G., Harlecki, A. Multi-objective
optimization of a medical robot model in transient states. Scientific Journal of Silesian University of Technology. Series
Transport. 2018, 99,
79-88. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2018.99.7.
Grzegorz ILEWICZ[1],
Andrzej HARLECKI[2]
MULTI-OBJECTIVE
OPTIMIZATION OF A MEDICAL ROBOT MODEL IN TRANSIENT STATES
Summary. The article describes the method for the
multi-objective optimization of a proposed medical robot model, which has been
considered in the form of a serial kinematic chain. In the assumed approach,
the finite element method was used in order to model the flexibility of
manipulator links. To speed up the optimization process, the response surface
method was applied, defining the so-called metamodel. In order to uncover the
optimal solution, a multi-objective genetic algorithm was used, guaranteeing
the optimality of the manipulator model in the Pareto sense. The optimization
process was carried out by analysing the selected case of the
manipulator’s dynamics. The proposed optimization method allows us to
minimize the mass of the manipulator while additionally ensuring the highest
possible stiffness of its structure and sufficient strength of its parts. Furthermore,
it offers the possibility to eliminate the natural frequency of vibrations of
the model close to the resonant frequency.
Keywords: medical robot;
dynamics; transient state; optimization; genetic algorithm; finite element
method
1. INTRODUCTION
Medical robots are used
in human surgical procedures all over the world, in such a way that
recovery is quick, postoperative scars are small and the surgery itself
involves no problems associated with classic endoscopic operations. Due to the
accuracy of positioning the endoscope, as well as the safety of the operation,
which is of paramount importance, the complexity of endoscopic surgery has
many technical problems, which remain unresolved and are constantly being
contemplated scientifically.
Issues related to the
dynamics of a medical robot (we can also include here the behaviour of the
robot in transient states), and in particular the problem with vibrations in
the effector (in the form of a surgical instrument), dominate medical practice.
When designing such types of robots, the aim is to minimize their mass (this is
tantamount to reducing the transverse dimensions of their parts, e.g., the
thickness of their walls). On the other hand, the goal is to increase the value
of the lowest (i.e., basic) natural frequencies of vibrations in the
manipulators, which in turn should require an increase, not a reduction,
in their mass. Thus, it can be seen that such set targets contradict each
other. Therefore, the weight of the robot should only be minimized in such a
way that its basic natural frequency of vibrations does not decrease beyond the
permissible (real) value, while the transverse dimensions of the parts should
not reduce their strength beyond the permissible limit.
Various models of the
dynamics of a medical robot have been published to date. For example, the
dynamics model of a robot was presented, which, including its control system,
was developed in MATLAB/Simulink. A dynamics model based on the usage of the
finite element method was also introduced. In [2], a model was presented, which
takes into account the surgical instrument load coming from the operated
tissue. Moreover, many other works have been published on the optimization of
the medical robot by consideration of the various criteria; among them, we can
indicate the following works: [1,3,4]. Meanwhile, equations used in finite
element methods can be found in the following section [6].
This work aims to
optimize the full model of the dynamics of the medical robot, taking into
account such criteria as mass, first natural frequency and static stress, as
well as stress in transient states with the adoption of restrictions on
criteria in the form of a safety coefficient and value of the first natural
frequency. The following dynamic equation is solved by using the finite element
method:
,
(1)
where:
- is a mass matrix
- a damping matrix
- a stiffness matrix
- a displacement vector
- a vector of external
forces
The
solution to Eq. (1) enables us to show the full strength of the model, which is
close to reality due to the consideration in subsequent iterations of
transitional states from previous forces and impacts.
Then,
on the basis of Eq. (2), we define the eigenvalue mechanical problem with
frequencies:
, 
(2)
where 
is the natural frequency. Eqs. (1) and
(2) are solved by using the finite element method.
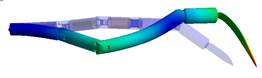
2. GEOMETRICAL MODEL OF A SURGICAL ROBOT
The
open kinematic chain of a medical robot considered in this work is shown in
Fig. 1. A medical robot has five links connected by three rotational
joints and one spherical joint.
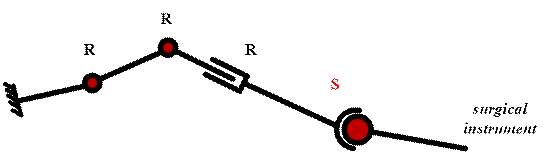
Fig. 1.
Serial chain of a medical robot with revolute and spherical joints in the RRRS
configuration
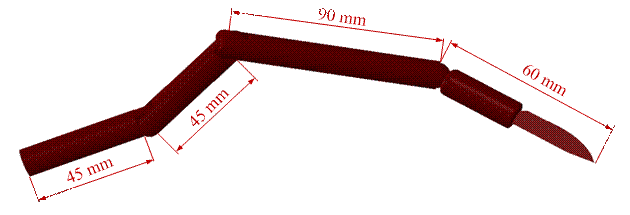
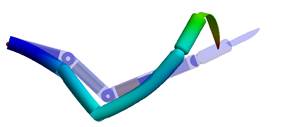
Fig. 2. Geometry model
of a medical robot with a serial chain
Fig.
2 shows the geometry of the robot’s kinematic chain whose dynamic is
deliberated in numerical experiments. The robot’s links are tubes, whose
wall thicknesses may change in the optimization experiment. The kinematic chain
with the presented configuration enables the tool to reach the back wall of the
operated organ or the serviced artificial organ inside the human body.
3. MODEL OF THE FINITE
ELEMENT METHOD
The geometric model of a
medical robot was discretized by a tetrahedral element of Solid 186. The robot
model was built of steel, due to its high strength as material of a real
object. It is important to obtain the required safety factor in order to
achieve the safety endurance of the robot. This task is extremely
intricate due to the minimization problems. This was shown in [7], where, due
to endurance reasons, the project of a Polish medical robot could not be
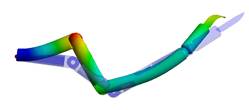
completed. Fig. 3 shows a geometric model with a mesh of finite elements.
Fig. 3. Mesh model of a
finite element method
The concurrence
of the numerical solution with the correct values was gained for the 26,778
nodes of the mesh model. This concurrence was acquired by increasing the number
of finite elements of the model until the value of the stress size stopped
changing or was only slightly oscillated around this value. Fig. 4 shows a
diagram of reduced stress according to the Huber-Mises hypothesis in the
static state.
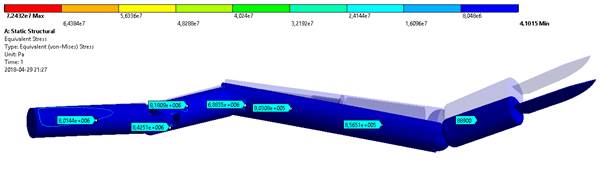
Fig. 4.
The value of reduced stress according to the Huber-Mises hypothesis for a
static load in the iso-tension chart
Fig.
5 shows the characteristics of tension for transient states. The system was
forced to move in the first degree of freedom at a velocity of 1 [rad/s].
A 20 force [N] originating from the interaction with tissue was applied to the
effector.
A
significant issue for the construction of a medical robot is the work in the
range of the resonance curve. It should be assumed that these vibrations
are not suppressed. They can come from propulsion systems, extortions from
tissue and functional activities, i.e., movements in the kinematic chain - in
other words, an effector movement over a given trajectory, which can be
displayed in T periods for a medical robot; as a function argument of a
frequency calculated as a number of oscillations per second, it may have a
resonant value in the quotient with an n. Therefore, it is important to
illustrate the models (shapes of vibrations and their qualities) during
resonance phenomena. Fig. 6 shows the first six shapes of vibrations for the
next natural frequencies that would appear during resonance phenomena.
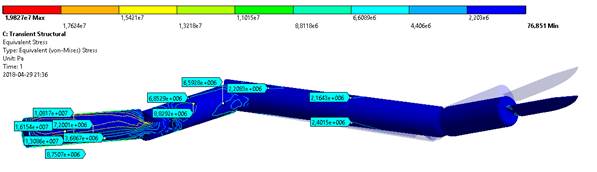
Fig. 5.
The value of the reduced stress according to the Huber-Mises hypothesis for
transient states in the iso-stress chart for movement in the first joint
|
|
|
|
First
natural frequency of 401.19 [Hz] |
Second
natural frequency of 479.3 [Hz] |
|
|
|
|
Third
natural frequency of 517 [Hz] |
Fourth
natural frequency of 1,102 [Hz] |
|
|
|
|
Fifth
natural frequency of 1,398 [Hz] |
Sixth
natural frequency of 3,143 [Hz] |
|
Fig. 6.
Qualitative charts of displacements during resonance for the next natural
frequencies looking from left to right side and from top to bottom |
|
The
first and second forms of vibrations define the lateral and longitudinal
vibrations, as do the third and fourth, respectively. For higher frequencies
torsional vibrations and vibrations with a more complex character appear. The
numerical model of a medical robot is characterized by the tuning ability
from the resonant curve.
4.
STRUCTURAL OPTIMIZATION MODEL
The
multi-objective optimization problem is defined in terms of finding the Pareto
front for such criteria as mass, first natural frequency, safety factor, and
stress in static and dynamic states. The optimization model is used to control
the mechanical parameters in order to achieve the optimal properties desired in
the design process. The major values are safety factor (the most important
value due to the most vital criterion for the medical robot; also for any other
construction), safety, balanced stiffness by its own frequency as a measure of
an accurate positioning of the robot and repeatability, and stress at rest and
in transient states, in which we know there are reactions inside the structure
and displacements. The limitation in the first natural frequency, from
which results the inflexibility of the construction, is said to be 60 [Hz]
(12.5 [Hz] is the smallest natural frequency, which was found for the
clinically used PUMA 560 medical robot).
The
optimization function can be described as:
.
(3)
The restrictions of the
model can be specified as:
,
.
In addition, other
restrictions must be met:
,
,
where:
- mass vector
- vector of the first natural frequency
- stress vector in the
static state
- stress vector in
transient states
, 
- dimensions, resulting in the wall
thickness of the first and second links
Limitations
to the geometrical dimensions have a functional character, i.e.,
it is assumed that a space must be left inside the structure for
mechanical linkages causing the movement. The optimization model is solved by
using the multi-objective genetic algorithm (MOGA) [5].
To
speed up the optimization process, the response surface method was used to
define the so-called metamodel, which is specified through the matching of approximating
functions to a set of points originating from a numerical experiment.
There are statistical functions that verify the accuracy of this match (the
basic one is the correlation coefficient R2, which should reach a
value close to 1 in the case of a proper match). In general terms, the response
surface is the approximate analytical dependence between input and output
values, which replaces the complex calculation algorithm. The response surfaces
are identified by using the so-called Kriging method (also called as the
spatial interpolation method). Finding the optimal solution is achievable
thanks to the use of the MOGA. The applied algorithm includes optimality in a
Pareto sense, based on non-dominated solutions, and provides a result in the
form of a global Pareto front. In the accepted procedure, such variable and
decisional values as d1
and d2 are searched, where
the objective function f({d})
will guarantee the smallest mass of the manipulator, the maximum value of the
first natural frequency, and sufficiently low values of equivalent stress in
the case of the static and dynamic load of the manipulator.
4. RESULTS
Figs.
7-9 show the response surfaces for mass, the first natural frequency and the
equivalent stress (transient state), depending on the dimensions of the medical
robot links. A very good fitting of a metamodel was gained in relation to the
data from numerical experiments, i.e., the coefficient of correlation R2
was equal to 1 for all criteria.
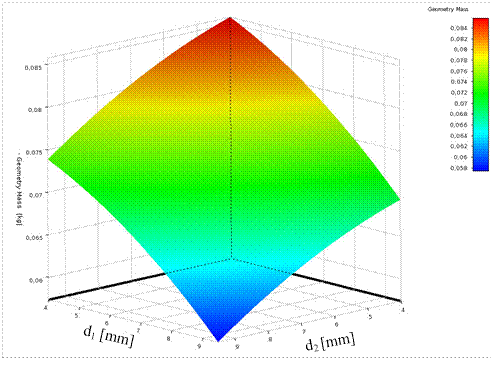
Fig. 7.
The response surface for mass and dimensions
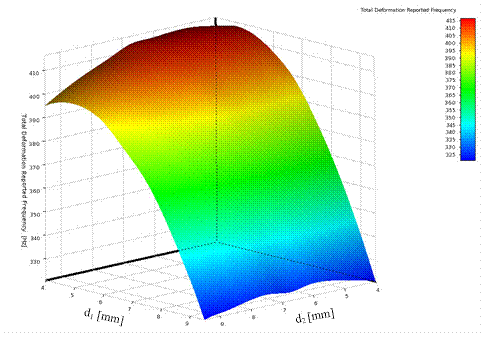
Fig. 8.
The response surface for frequency and dimensions
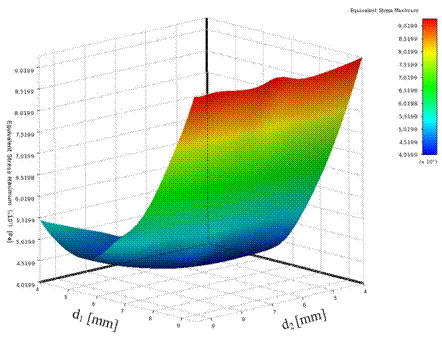
Fig. 9.
The response surface for equivalent stress (transient state) and dimensions
Fig.
10 shows a graph of sensitivity towards criterions when changing the geometric
dimensions for the optimal obtained solution. The graph should be read in such
a way that each criterion field is composed of the percentage effect of a
dimensional variable marked in colour on its value.
After
obtaining the metamodel, a genetic algorithm was used to select the optimal
non-dominated solution on the basis of the Pareto front.
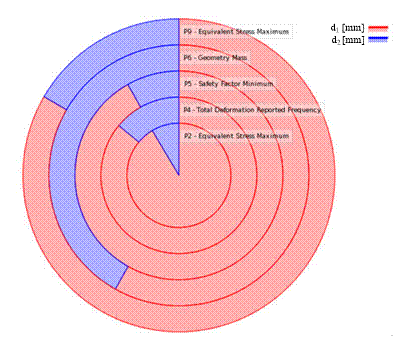
Fig. 10.
The graph of sensitivity dimensions towards criterions
It
was agreed that the solution would be a Pareto point, for which the mass
is minimal, the first natural frequency is maximal and greater than 60 [Hz],
and the safety factor is greater than or equal to 4. Using the genetic
algorithm, the following values of mechanical quantities were achieved:
first natural frequency of 408.33 [Hz] and mass of 0.075 [kg]. At the same
time, a minimum static stress of 3.1E7 [Pa] and a minimum stress in transient
states equal to 4.1E7 [Pa] were gained. These were acquired for the
geometric dimensions d1=5.2 [mm] and d2=6.2 [mm] and a
safety factor equal to 7.8.
5.
CONCLUSIONS
This
work proposes a model of dynamics including the solution for a full
Newton’s equation for the deformable block in the non-inertial system.
The finite element method has been applied, which is characterized by a good
approximation of actual dynamics states in a numerical manner, as
well as being the basic method of choice for the structural analysis of systems
with complex geometry and load condition, taking into account the forces
appearing in the motion. Deformations from previous states were included in
each subsequent iteration of the analysis. To date, this medical robot model
has not been reported in the literature for which a multicriterion optimization
experiment has been carried out. The results of optimal mass and stiffness
for a medical robot were obtained for the given limits. The achieved numerical
model allows for the real object to be tuned from the resonant ranges. In
further works, the numerical model will be applied to a model with a DC motor
and a control system based on the PID regulator.
References
1.
Grebenişan
G., N. Salem. 2017. “The multi-objective
genetic algorithm optimization of a superplastic forming process, using
Ansys”. In: Proceedings of the International Conference
IMT Oradea. 27-29 May 2017. Baile Felix, Romania. ISSN: 2261236X.
DOI: 10.1051/matecconf/201712603003.
2.
Yang J., L. Yu, L. Wang, Z. Wang, W. Wang. 2017. “Dynamic
modeling and analysis of the instrument arm based on the physical properties of
soft tissues”. In: Proceedings of
the Institution of Mechanical Engineers Part C: article in press. ISSN:
09544062. DOI: 10.1177/0954406217715661.
3.
Li Jianmin, Shuxin Wang, Xiaofei Wang, Chao He. 2010.
“Optimization of a novel mechanism for a minimally invasive surgery
robot”. International Journal of
Medical Robotics and Computer Assisted Surgery 6 (1): 83-90. ISSN:
1478-5951. DOI: 10.1002/rcs.293.
4.
Miroir M., J. Szewczyk, O.Y. Nguyen, S. Mazalaigue, A.B. Grayeli, O.
Sterkers. 2009. “Mechanical design and optimization of a microsurgical
robot”. In: Proceedings of Eucomes 08, The Second
European Conference on Mechanism Science: 575-583. 17-20 September 2008.
Cassino, Italy. ISBN: 978-1-4020-8914-5.
DOI: 10.1007/978-1-4020-8915-2_69.
5.
Wang
Wei, Weidong Wang, Wei Dong, Hongjian Yu, Zhiyuan Yan, Zhijiang Du. 2015.
“Dimensional optimization of a minimally invasive surgical robot system
based on NSGA-II algorithm”. Advances
in Mechanical Engineering 7 (2): 83-90. ISSN: 1687-8140.
DOI: 10.1177/1687814014568541.
6.
Zienkiewicz
Olek, Robert Taylor, J.Z. Zhu. 2013. The Finite Element Method: Its Basis
and Fundamentals.
Oxford: Elsevier Ltd. ISBN: 9781856176330.
7.
Leniowska
Lucyna, Leniowski Ryszard. 2016. “Technological limitations of surgical
robotics on the example of a robot Roch-1”. Acta
Bio-Optica et Informatica Medica
2(3). ISSN: 1234-5563.
Received 29.02.2018; accepted in revised form 30.05.2018
Scientific
Journal of Silesian University of Technology. Series Transport is licensed
under a Creative Commons Attribution 4.0 International License