Article
citation information:
Grega, R., Krajňák, J.,
Moravič, M. Experimental verification of the impact of a technical gas-using
pneumatic coupling on torsional oscillation. Scientific Journal of Silesian University of Technology. Series
Transport. 2018, 99, 53-63.
ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2018.99.5.
Robert GREGA[1],
Jozef KRAJŇÁK[2],
Marek MORAVIČ[3]
EXPERIMENTAL
VERIFICATION OF THE IMPACT OF A TECHNICAL GAS-USING PNEUMATIC COUPLING ON
TORSIONAL OSCILLATION
Summary. The field of reducing torsional vibration of
mechanical systems has seen the emergence of new flexible coupling designs. Our
attention is focused on flexible pneumatic couplings. The flexible member of
this coupling design is a pneumatic bag. The typical basic feature of such
couplings is that the pneumatic bag allows for a change in air pressure. In the
course of developing pneumatic couplings, we have experimented with the use of
technical gases other than air for filling pneumatic bags. The aim has been to
verify the impact of pneumatic couplings filled with other technical gases on
the magnitude of torsional vibration in the mechanical system. For verification
itself, two different gases have been used: helium, whose density is lower than
air density, and propane butane, whose density is higher than air density.
Experimental verification was performed under laboratory conditions on a
mechanical system where torsion vibration was produced by a piston compressor.
Keywords: technical gases;
torsional vibration; pneumatic flexible coupling; mechanical system
1. INTRODUCTION
Any joint alignment of machines
transmitting mechanical motion may be considered as mechanical system. The
motion transmitted by the mechanical system may be continuous or variable. In
particular, it is often the case that the variable motion is the source of
excessive strain. In technical practice, variable motion is the source of
vibration. If the variable motion is transmitted by a mechanical system that
rotates, the vibrations that are generated are known torsional vibrations [1].
Vibrations are therefore an
indispensable part of every mechanical system; they cannot be removed, but it
is possible to reduce their impact [2-7]. The most critical are vibrations that
originate in the form of resonance or in the system’s vicinity [8]. These
conditions must be avoided as they cause breakdowns, such as the breakage of
shafts and cog wheels, defects in connecting components, and impressions on
springs and grooved shafts.
Several effective ways of avoiding
resonance or reducing the impact of vibrations are currently available. In the
area of torsional vibrations, a flexible coupling is recommended for use in the
mechanical system [9].
Extensive innovation is currently
underway, targeting mechanical systems suffering from torsional vibration. In
addition to upgrading technical systems, attention needs to be paid to their
reliability [10-12].
Considerable progress has been
noted in the area of flexible coupling design as well [13,14]. The couplings
need to meet the high demands placed on them, as they have to be able to
transmit large torques, while sufficiently reducing the magnitude of torsional
vibrations at the same time [15,16].
Various additional elements are
starting to be used in flexible coupling design to increase their functionality
and usability. For this purpose, elements such as shock absorbers, torsional
vibration eliminators, planetary gears, springs with different degrees of
stiffness and flexible discs are applied therein [17-19]. A special group of
flexible couplings is represented by pneumatic flexible couplings, which are
characterized by the fact that, as flexible elements, pneumatic bags are
incorporated into their design. It is possible to vary the air pressure in
pneumatic bags and thus change the coupling characteristics. Therefore, it is
possible to talk about a typical load-applying fields rather than about the
coupling loading characteristics [20]. Thus, if a pneumatic coupling has a
load-applying field of characteristics, it also has a range of degrees of
torsional stiffness. An undeniable advantage is the possibility to change this
torsional stiffness continuously during the operating mode of the mechanical
system.
The use of technical gases for the
filling of pneumatic bags of the flexible coupling also has innovative and
research potential. Technical gases are easily available common gases used in
industrial technological applications. Technical gases can change their
pressure [21,22]. They have different properties than air and therefore it is
to be expected that, when applied in pneumatic flexible couplings, they will
have a different effect on the magnitude of torsional vibration in the
mechanical system. We have examined the applicability of selected technical
gases in pneumatic couplings under our own laboratory conditions. We found that
they had an effect on the change in some of the features of the pneumatic
couplings. We decided to experimentally verify the application of a pneumatic
flexible coupling using technical gases in a mechanical system impacted by
torsional vibration.
Our aim was therefore to
experimentally verify the change in the magnitude of torsional vibration in the
mechanical system, in which the pneumatic flexible coupling would be filled
with different technical gases.
2. MATERIAL AND METHODS
We used three gases to
verify the influence of technical gases on the magnitude of torsional
vibration. The first gas was air. At the same time, we used air as the
reference gas. We chose helium and propane butane as the two other gases to be
compared with air. These gases were chosen on the basis that they are commonly
available. Furthermore, one of them has a lower density and the other a higher
density.
The occurrence of helium
on earth is very rare. Due to its extremely low weight, it is only found in
higher layers of the earth’s atmosphere. Smaller quantities thereof are
also found in natural gas from which it is obtained by freeze-drying.
Occasionally, helium also rises from cracks in the earth. Due to its extremely
low density and inert behaviour, helium is used to fill balloons and airships
as a replacement for flammable hydrogen. A significant disadvantage is its
relatively high price. In addition, the helium atom is of a very small
diameter, enabling the helium to diffuse easily through solids, which
translates into its losses [23-25]. For the purpose of our measurements, HE-4.6
helium was used. The technical gas contained 99.996% helium.
The propane butane used
in the experiment consisted of 50% propane and 50% butane. Under normal
conditions, propane butane is gaseous, but it can be converted into its liquid
form relatively easily by cooling or compression. In its liquid state, it only
takes up a 260th of its gaseous volume. The density of this gas is higher than
that of the air; it is also flammable. Tab. 1 shows the basic properties of the
technical gases used.
Tab. 1.
Basic physical properties of individual gases
|
Helium He |
Air |
Propane-butane C3H8+C4H10 |
|
|
Specific gas constant r [J kg-1 K-1] |
2,079 |
287.04 |
163.39 |
|
Gas density [kg.m-3] (15°C) |
0.176 |
1.276 |
2.145 |
|
Molecular weight [kg kmol-1] |
4.003 |
28.966 |
50.102 |
Tab. 1 makes it apparent that the gas density of helium is seven times
lower than that of air, while the density of propane butane is twice as high as
air density. Furthermore, the situation is similar when it comes to the
molecular weight of the gases. The greatest value is that of propane butane,
while the smallest is that of helium. The change is obvious when we look at the
specific gas constant, where helium has the highest value and propane butane
has the lowest. When compared to air, these value ratios are similar to gas
density ratios.
The experimental gases were used to fill in a pneumatic coupling of the
4-2/70 T-C type (see Fig. 1).

Fig. 1.
4-2/70 T-C pneumatic flexible coupling
Pneumatic coupling transmits the torque via four flexible
double-corrugated pneumatic bags evenly distributed over the circumference,
which serve as flexible chambers. The flexible chamber’s radius is 83.5 mm
from the coupling axis. The height of the elastic bags in neutral position is
90 mm and the diameter is 70 mm. The maximum permissible deformation of the
elastic bags is 25 mm in both directions of rotation, determining the maximum
coupling twist of 11.5°. The elastic bags are interconnected and attached
to steel discs.
3. PREPARATION FOR LABORATORY
EXPERIMENT
The experiments designed to verify the torsional
vibration change induced by the use of technical gases were performed under
laboratory conditions in our workplace. The mechanical system employed in the
experiments is shown in Fig. 2.
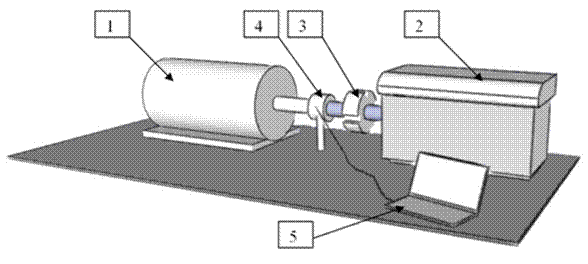
Fig. 2. Scheme
of the experimental mechanical system
The mechanical system is designed with an
incorporated source of torsional vibration, as well as to allow different speed
modes. As a source of torsional vibration, a three-cylinder air compressor (2),
of the ORLIK 3JSK-75 type, with the output of 50 m3.h-1, was used. The
compressor had a cylinder diameter of 82 mm, a piston stroke of 70 mm and a
maximum working pressure of 10 bars. The compressor was driven by a three-phase
asynchronous electric motor (1), whose speed was continuously variable with a
frequency converter from Siemens, with vector control. The nominal output of
the electric motor was 11 kW and the nominal speed was 1,470 min-1.
The above-described pneumatic coupling of the 4-2/70 T-C (3) type and a torque
sensor (4) were placed between the compressor and the electric motor. The
torque sensor was manufactured by MOM Kalibergyár, Type 7934s, with the
measuring range: 0 ÷ 500 Nm, with the accuracy of 0.5 N.m. The torque
sensor was further connected to the measuring and evaluation apparatus (5). The
apparatus was of a universal type: Quantum MX 840 with eight individual
measurement channels and individual sample rates up to 40 kS/s per channel.
Using this measuring chain, time domain signals were
mapped. Signal analysis can also be used appropriately for transition states,
while total torsional vibrations can be conveniently determined from the time
signal. Our effort was to determine the effective speed value, known as RMS,
from the time signal. This parameter appropriately reflects the energy that is
converted to vibrations and therefore a trusted indicator of the state of the
machine in terms of vibration magnitude. This parameter is also a suitable
parameter for vibration comparisons. The effective vibration value was sought
for an operating speed from 200 to 1,500 min-1. Experimental
measurements were performed with a step change in revolutions after 100 min-1.
Subsequently, the RMS vibration values measured for each revolution were
translated into the envelope curve. The measurements were performed for all
gases under examination. The gas pressure in the pneumatic coupling varied
between 100 and 600 kPa stepwise every 100 kPa. RMS vibration values were
detected and recorded for all technical gases pressures.
4. RESULTS AND DISCUSSION OF
EXPERIMENTS
With the help of experimental
measurements, we wanted to identify the impact of technical gases in the
pneumatic coupling on the magnitude of torsional vibration. Dependencies were
made using the values obtained in individual measurements; see Figs. 3-8. For
the sake of chart clarity, the dependencies found in the measurements on the
pressure of the technical gases at 200, 400 and 600 kPa are provided.
The experimental measurements and the evaluated records show that
dynamic proportions of the whole mechanical system can be affected by the
flexible pneumatic coupling and the varying pressure of all investigated gases.
Figs. 3-5 show the dependence of torque vibration on operating speed. As
evident from all the figures, changing the pressure of the studied gases
translates into a change in the resonance area. For all three gases, the
resonant area of the mechanical system shifts to the lower speed range with
decreasing pressures in the pneumatic coupling. The displacement in the
resonant area is the same for all three gases and, as indicated by the
measurements, depends only on the gas pressure in the pneumatic coupling. By
comparing the dependencies, it can be observed that, in the case of air and
helium, the torsional vibration value increases with increasing pressure,
whereas, in the case of propane butane, the torsional vibration value increases
up to 400 kPa. When this value is exceeded, however, the torsional vibrations
decrease with increasing pressures.
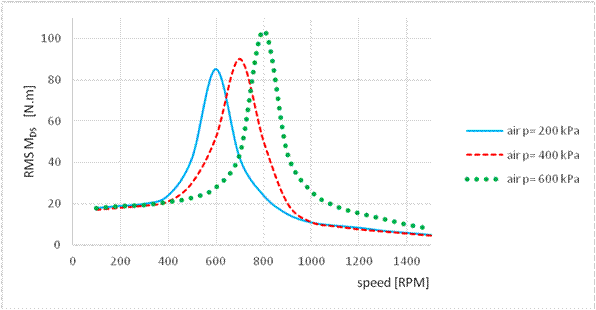
Fig. 3. Envelope curve
of RMS values for the torsional vibration in the mechanical system
with a pneumatic
flexible coupling filled with air at p=200 kPa, p=400 kPa, p=600 kPa
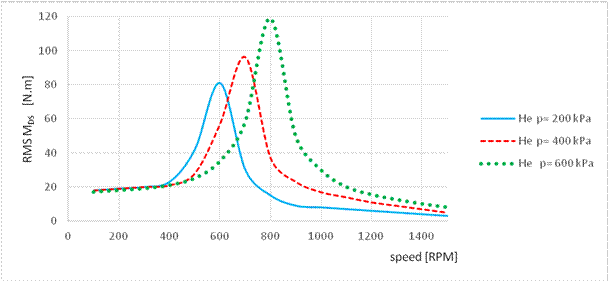
Fig. 4. Envelope curve
of RMS values for the torsional vibration in the mechanical system
with a pneumatic
flexible coupling filled with helium at p=200 kPa, p=400 kPa, p=600 kPa
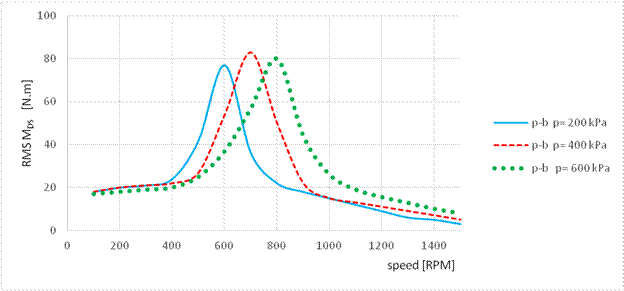
Fig. 5. Envelope curve
of RMS values for the torsional vibration in the mechanical system
with a pneumatic
flexible coupling filled with propane butane at p=200 kPa, p=400 kPa, p=600 kPa
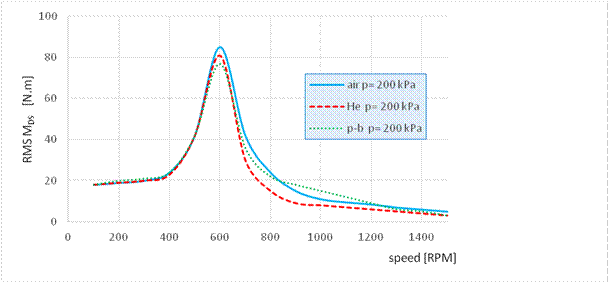
Fig. 6. Envelope curve of RMS
values for the vibration in the mechanical system with a flexible pneumatic
coupling filled with air, helium and propane butane, respectively, at 200 kPa
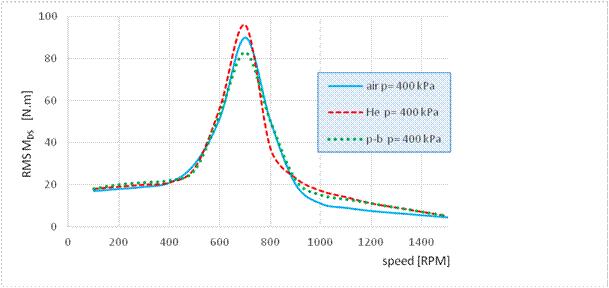
Fig. 7. Envelope curve of RMS
values for the torsional vibration in the mechanical system with a flexible
pneumatic coupling filled with air, helium and propane butane, respectively, at 400
kPa
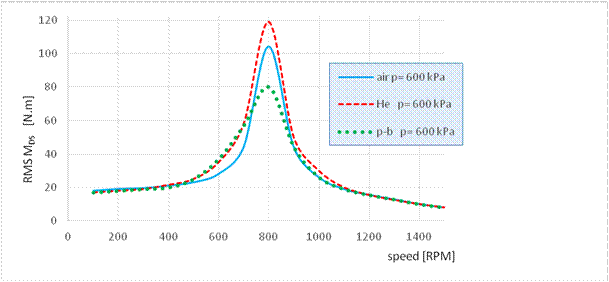
Fig. 8. Envelope curve of RMS
values of the torsional vibration in the mechanical system with a flexible
pneumatic coupling filled with air, helium and propane butane, respectively, at 600
kPa
In order to compare the impact of the technical gases at the same
pressures and speed, we have created dependencies, as shown in Figs. 6-8. It is
clear from these dependencies that the most significant reduction in the
vibration value in the region of resonance is achieved when the pneumatic
coupling is filled with propane butane. This condition applies to all the
compared pressures. Interestingly, at lower pressures of up to 200 kPa, the
lowest vibration value is shown by the pneumatic coupling filled with helium.
Starting with the pressure of 200 kPa and greater, the pneumatic coupling
filled with helium has the lowest impact on torsional vibration, and thus
achieves significantly higher torsional vibration values than the pneumatic
coupling filled with air and propane butane.
In
the subresonance area, which is also of interest, the torsional vibration
values for all the compared gases are the same. In the area above the resonance
level, the torsional vibration values for the individual gases differ by up to
400 kPa; but, at the pressure of 600 kPa, the torsional vibration values are
again the same in the area above resonance.
5.
CONCLUSION
From the analysis of the
courses of the measured magnitude of RMS torsional vibrations, it can be stated
that the change in the pressure in all three technical gases in the pneumatic
coupling bags also changes the magnitude of torsional vibration in the
mechanical system.
The measured values of
torsional vibrations show the impact of technical gas pressure on the
occurrence of a resonance area. Furthermore, experimental measurements verify
that technical gases affect the vibration value in the resonance area. The
difference between the resonance values is as much as 30% if the pressure in
the pneumatic coupling is 600 kPa. The greatest impact on torsional vibration
in terms of resonance concerns propane butane, while the lowest impact involves
Helium. Different physical properties of the technical gases affect torsional
vibration, especially in the resonance area. Although the difference in the density
of the studied gases is more than sevenfold, under increasing pressure in the
region of resonance, the torsional vibration difference is 150%. Thus, the
difference in gas density does not appear to be proportional to the change in
torsional vibrations. Two basic findings can be postulated from the
experimental measurements:
1. The type of technical gas in the pneumatic coupling does not
affect the location of the resonance area of the mechanical system. Only the
value of the technical gas pressure in the pneumatic coupling affects the
occurrence of the resonance area in the mechanical system. With increasing
pressure, this area shifts to the higher revolution range.
2. If the mechanical
system with applied pneumatic coupling is located in the resonance area, the
magnitude of the torsional vibration is strongly impacted by the type of
technical gas in the pneumatic coupling. If a higher density gas is used, the
torsional vibration value will decrease.
The
presented results confirm the fact that the use of technical gases other than
air in pneumatic couplings can be applied in the field of mechanical protection
against torsional vibration. Such use may be especially beneficial to
mechanical systems operating close to the resonance area, where it may be efficient
to use technical gases of a higher density than air.
Acknowledgements
This work is a part of the
following projects: KEGA - 041TUKE-4/2017, VEGA 1/0473/17 and VEGA 1/0110/18.
References
1.
Murawski Lech, Adam Charchalis. 2014.
“Simplified method of torsional vibration calculation of marine power
transmission system”. Marine
Structures 39: 335-349, ISSN: 0951-8339.
2.
Pisarski Dominik, Czesław I Bajer, Bartłomiej Dyniewicz,
Jacek M Bajkowski. 2016. “Vibration control in smart coupled beams
subjected to pulse excitations”. Journal
of Sound and Vibration 380: 37-50. ISSN: 0022-460X. DOI:
10.1016/j.jsv.2016.05.050.
3.
Jakubovičová
Lenka, Milan Sága, Peter Kopas, Marian Handrik, Milan Vaško. 2010. “Some notes on analysis of bending and
torsion combined loading”. Machine
Dynamics Research 34(3): 97-105. ISSN: 2080-9948.
4.
Czech
P. 2013. “Intelligent Approach to Valve Clearance Diagnostic in
Cars”. Activities of Transport Telematics. TST 2013. Communications in Computer and Information Science 395: 384-391.
DOI: https://doi.org/10.1007/978-3-642-41647-7_47.
5.
Czech
P., Mikulski J. 2014. “Application of Bayes Classifier and Entropy of
Vibration Signals to Diagnose Damage of Head Gasket in Internal Combustion
Engine of a Car”. Telematics - Support For Transport. TST 2014. Communications in Computer and Information
Science 471: 225-232. DOI: https://doi.org/10.1007/978-3-662-45317-9_24.
6.
Figlus Tomasz, Jozef Gnap, Tomas Skrucany, Branislav Sarkan, Jozef
Stoklosa. 2016. „The Use of Denoising and Analysis of the Acoustic Signal
Entropy in Diagnosing Engine Valve Clearance”. Entropy 18(7). Article Number: 253.
7.
Figlus Tomasz, Stefan Liscak. 2014. „Assessment of the
vibroactivity level of SI engines in stationary and non-stationary operating
conditions”. Journal Of
Vibroengineering 16(3): 1349-1359.
8.
Becerra,
J.A., F.J. Jimenez, M. Torres, D.T. Sanchez, E. Carvajal. 2011. “Failure analysis of reciprocating
compressor crankshafts”. Engineering
Failure Analysis 18(12): 735-746. ISSN: 1350-6307.
https://doi.org/10.1016/j.engfailanal.2010.12.004.
9.
Kim Gi
- Woo, Soon- Chul Shin. 2015. “Research
on the torque transmissibility of the passive torsional vibration isolator in
an automotive clutch damper”. Proceedings
of the Institution of Mechanical Engineers Part D: Journal of Automobile Engineering
229(13): 1840-1847. ISSN: 0954-4070.
10. Bakowski H. J. Piwnik. 2016.
„Quantitative and qualitative comparison of tribological properties of
railway rails with and without heat treatment”. Archives Of Metallurgy
And Materials 61(2): 469-474. DOI: 10.1515/amm-2016-0037.
11. Bakowski H., A. Posmyk, J. Krawczyk. 2011.
„Tribological properties of rail steel in straight moderately loaded
sections of railway tracks”. Archives Of Metallurgy And Materials 56(3):
813-822. DOI: 10.2478/v10172-011-0090-0.
12. Kulka Jozef, Martin Mantic, Gabriel
Fedorko, Vieroslav Molnar. 2016. “Failure
analysis of increased rail wear of 200 tons foundry crane track”. Engineering
Failure Analysis 67: 1-14. ISSN: 1350-6307. DOI:
10.1016/j.engfailanal.2016.05.032.
13. Homišin Jaroslav, Matej Urbanský.
2015. “Partial results of extremal control of
mobile mechanical system”. Diagnostyka
16(1): 35-39. ISSN: 1641-6414.
14. Li Wanyou, Zhuoye Chai, Mengqi Wang. 2016.
“Online identification and verification of
the elastic coupling torsional stiffness”. Shock and Vibration. ISSN: 1070-9622.
15. Charles P., Jyoti Sinha, Fengshou Gu, L. Lidstone, Andrew David
Ball. 2009. “Detecting the crankshaft torsional
vibration of diesel engines for combustion related diagnosis”. Journal of Sound and Vibration 321(3-5):
1171-1185. ISSN: 0022-460X. DOI: 10.1016/j.jsv.2008.10.024.
16. Pavlikova Ľudmila,
Beata Hricová, Ervín Lumnitzer. 2018. “Acoustic camera as a
tool for identifying machinery and equipment failures”. Advances in Science and Technology Research
Journal 12: 322-328. DOI: 10.12913/22998624/87110.
17. Sapieta Milan,
Alžbeta Sapietová, Vladimír Dekýš. 2017. “Comparison of
the thermoelastic phenomenon expressions in stainless steels during cyclic
loading”. Metalurgija 56 (1-2):
203-206. ISSN: 0543-5846.
18. Galvagno Enrico, Mauro Velardocchia,
Alessandro Viglianif. 2011. “Dynamic
and kinematic model of a dual clutch transmission”. Mechanism and Machine Theory 46: 794-805. ISSN: 0094-114X.
19. Pfabe Mathias, Christoph Woernle.2016. “Reducing torsional vibrations by means of
a kinematically driven flywheel - theory and experiment”. Mechanism and Machine Theory 102: 217-228. ISSN: 0094-114X.
20. Homišin Jaroslav, Peter
Kaššay. 2014. “Optimal tuning of torsional oscillating
mechanical systems”. In: Proceedings
of 54th International Conference of Machine Design Departments: Modern Methods
of Construction Design: 63-69. 10-12 September 2013. Department of the
Design of Machine Elements and Mechanisms, Technical University of Liberec,
Hejnice, Czech Republic. ISBN: 978-3-319-05203-8. DOI:
10.1007/978-3-319-05203-8_9.
21. Samociuk W., Z. Krzysiak, G. Bartnik, A.
Skic, S. Kocira, B. Rachwal, H. Bakowski, S. Wierzbicki, L. Krzywonos.
2017. „Analysis of explosion hazard on propane-butane liquid gas
distribution stations during self tankage of vehicles”. Przemysl Chemiczny 96(4): 874-879. DOI:
10.15199/62.2017.4.29.
22.
Mikulski M., S. Wierzbicki, M. Smieja, J. Matijosius. 2015. „Effect of CNG in a fuel dose
on the combustion process of a compression-ignition engine”. Transport 30(2): 162-171.
23. Sunarso Jaka, Siti Salwa Hashim, Jerry
Y.S. Lin, Shaomin Liu. 2017. “Membranes
for helium recovery: an overview on the context, materials and future
directions”. Separation and
Purification Technology 176: 335-383.
ISSN: 1383-5866.
24. Dehdashti Jahromi, H. Farrokhpour. 2017. “Effect of helium nanoclusters on the
spectroscopic properties of embedded SF6: ionization, excitation and
vibration”. Spectrochimica Acta
Part A: Molecular and Biomolecular Spectroscopy 173: 772-782. ISSN: 1386-1425.
25. Maruschak P., S. Panin, I. Vlasov, O.
Prentkovskis, I. Danyliuk. 2015. „Structural levels of the nucleation and
growth of fatigue crack in 17Mn1Si steel pipeline after long-term
service”. Transport 30(1):
15-23.
Received 10.02.2018; accepted in revised form 12.05.2018
![]()
Scientific
Journal of Silesian University of Technology. Series Transport is licensed
under a Creative Commons Attribution 4.0 International License