Article citation information:

Wieczorek, A.N. Analysis of lubrication conditions for angle planetary gearboxes applied in mining scraper conveyors. Scientific Journal of Silesian University of Technology. Series Transport. 2018, 98, 191-199. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2018.98.18.

Andrzej N. WIECZOREK[1]

ANALYSIS OF LUBRICATION CONDITIONS FOR ANGLE PLANETARY GEARBOXES APPLIED IN MINING SCRAPER CONVEYORS

Summary. The paper presents calculations of the relative oil film value for the meshing of angle planetary gearboxes used in mining scraper conveyors. Calculating the value of this parameter was made using methodology that was compliant with ISO/TR 15144-1: 2014 (E). As a result of the analysis, it was found that exploitation of mining gears takes place under boundary or mixed lubrication conditions, with oil viscosity and surface roughness having a significant influence on these conditions.

Keywords: scraper conveyor, planetary gear, wear, lubrication

1. INTRODUCTION

The main purpose of lubrication [1] is to transform the friction of external contacting elements into the friction inside the lubricant layer. The formation of a relatively permanent layer that separates mating surfaces may be caused by physisorption of polar particles on friction surfaces, chemisorption of small boundary layers generated as a result of tribochemical processes, or by hydrodynamic or elasto-hydraulic effects.

With respect to elements of gearboxes, such as gear wheels, it is essential to create, under conditions of elasto-hydraulic lubrication (a diagram of the elasto-hydrodynamic contact zone of involute profile teeth, along with a specification of the actual surface deformation, is presented in Figure 1), a layer that separates mating surfaces in order to ensure their high operating durability. The thickness of this layer is characterized by a certain parameter, i.e., the minimum design thickness of the lubricant layer, hmin (also referred to in this paper as the oil film thickness). This parameter is characterized by the size of the lubrication gap formed as a result of the action of the load and the movement of mating surfaces (Figure 2). The thickness of this layer depends on a number of design and operational factors, as well on the parameters of the lubricant (this problem is described in more detail in the next section). Lubrication conditions depend not only on the thickness of the lubricant film, but also on the roughness of mating surfaces.

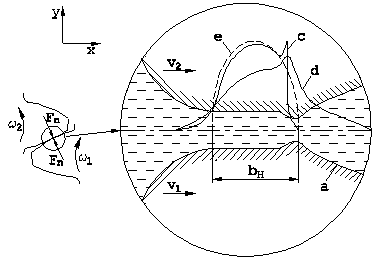
Fig. 1. The zone of the elasto-hydrodynamic contact of the teeth, taking into account the actual deformation of the surface (a), pressure distribution (c) and temperature (d) in the lubricant layer against the Hertzian distribution of static pressures (e); designations: ω₁, ω₂ – angular velocities of gear wheels, v₁, v₂ – tangential velocities in the contact zone, F_n – normal teeth load, b_H – width of the elastic Hertzian deformation

The parameter characterizing the degree of separation of mating surface irregularities, and thus the type of friction occurring between these surfaces, is the relative thickness of the oil film, λ, determined by the following relationship:

(1)

where Rq_1,2is the surface roughness (RMS).

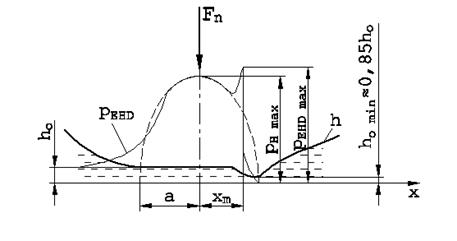
Fig. 2. Pressure distribution p_EHD and the shape of the lubrication gap h in the elasto-hydrodynamic contact (EHD) between surfaces and the lubricant [1]

The parameter Rq can be determined from the following formula [5]:

(2)

Boundary lubrication occurs when the parameter λ ≤ 1. A mixed friction occurs for the following range of the oil film thickness: 1 <λ <3. In turn, in the range of values λ = <3,10>, conditions for liquid lubrication EHD are generated (a comprehensive description of the theory of the elasto-hydrodynamic lubrication EHD can be found in [5]), which are characterized by the occurrence of an oil film layer with a thickness exceeding the surfaces’ irregularities. Above the relative value of the oil film thickness λ> 10, liquid friction (HD) occurs [2-4].

2. ASSUMPTIONS FOR CALCULATIONS AIMED AT DETERMINING THE MINIMUM THICKNESS OF THE LUBRICANT LAYER

In this study, the method described in the ISO/TR 15144-1: 2014 (E) [6] standard, which is based on the Dowson and Higginson studies [3], was used to calculate the minimum thickness of lubricant layer h_min.

In this method, Equation (2) takes the following form:

(3)

where R’ is the radius of curvature, U is the speed parameter, W is the load parameter, G is the material parameter and S is the temperature parameter.

In ISO/TR 15144-1: 2014 (E), the calculations of the relative value of the oil film thickness λ are only carried out for five characteristic points on the engagement section (Points A, B, C, D and E). For this study, it has been assumed that the values of the oil film thickness are to be determined for 106 other points of the engagement section.

In order to determine the minimum thickness of the lubricant layer, hmin, geometrical parameters of the teeth of the spur gear stage of a right-angle planetary gearbox (with the gear ratio i=39; Figure 3), used in mining armoured face conveyors (Table 1 summarizes the geometrical parameters of the teeth), and the load values corresponding to the power of driving motors (250, 315 and 400 kW; Table 2 shows the values of torque and rotational speed for this stage depending on the power of the driving motor) were adopted for the calculations. In addition, a decision was made to perform calculations for mineral oils in the range of viscosity classes VG68–VG460 (Table 3 summarizes the parameters of these oils) and for the range of surface roughness Ra=0.15-2 μm.

Fig. 3. A view of the right-angle planetary gearbox used in the drive of mining armoured face conveyors

Tab. 1

Parameters of the gear wheels subjected to various technological processes

Parameter	Symbol	Pinion	Gear wheel
Number of teeth	z	23	67
Module pitch, mm	m	7.5
Pressure angle, °	α	20
Teeth width, mm	b	120		120
Tooth root filled radius	ρ	0.380·m
Accuracy class	-	6

Tab. 2

Basic geometrical parameters of gear wheels of the right-angle spur planetary gearbox

Driving motor power, kW	250	315	400
Input torque of the gear stage, Nm	5,760	7,255	9213
Input rotational speed of the gear stage, RPM	414

Tab. 3

List of parameters characterizing the examined mineral lubricating oils

Viscosity grade of oil	Kinematic viscosity at 40°C, mm²/s (cSt)	Kinematic viscosity at 100°C, mm²/s (cSt)	Density at 15°C, kg/m³
VG68	68	8,7	887
VG100	100	11,4	891
VG150	150	15,0	887
VG220	210	18,5	895
VG320	320	25,0	903
VG460	460	30,8	904

3. CALCULATION RESULTS

When analysing possible solutions for the technical and economic problems mentioned, the calculation results concerning the relative value of the oil film thickness λ, as a function of the position of gear wheels of the gearbox on the engagement section, are as presented in Figure 4.

When analysing the curve presented in the figure above, it can be concluded that the smallest values of the λ parameter are observed at a single-tooth engagement point (Point B) of the engagement section. The lubrication conditions of the gearbox just at this point of the engagement section were adopted for the purposes of further analysis. Figure 5 shows plots of the relative oil film thickness λ, as a function of the power of the driving motor, and the viscosity grade determined for the roughness Ra=0.4 μm, while the plots in Figure 6 refer to the roughness Ra=0.8 μm.

Figure 7 presents plots of the relative oil film thickness λ, as a function of the surface roughness, and the viscosity grade determined for the driving motor power P=315 kW.

Taking into account the results presented in Figures 5-7, the following observations can be made:

- The relative thickness of the oil film determined for the roughness Ra = 0.8 μm, regardless of the load and type of oil, takes the values lower than 1 (λ <1)

- The relative thickness of the oil film determined for the roughness Ra=0.4 μm, for the majority of the load and oil values considered, takes values lower than 1 (λ <1); values λ> 1 are observed only for the motor power range P=50-150 kW, and for the oil with the viscosity grade VG460, as well as for the motor power P= 0 kW and for the oil with the viscosity grade VG320

- The relative thickness of the oil film determined for the motor power P=315 kW, for the majority of the load and oil values considered, takes values lower than 1 (λ <1); values λ> 1 are observed only for the viscosity grades VG150-460 and for the roughness Ra=0.15 μm, as well as for the oil with the viscosity grade VG460 and for the roughness Ra=0.25 μm

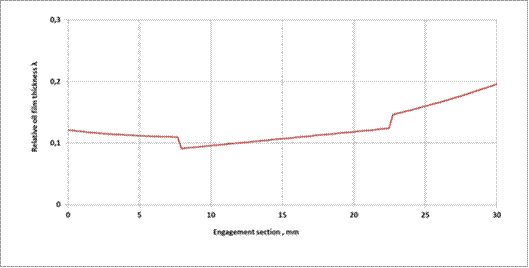
Fig. 4. The plot of the relative oil film thickness λ as a function of the position on the engagement section for the second stage of the right-angle spur planetary gearbox
(the results obtained for motor power P=315 kW, viscosity grade VG320 and roughness Ra=1 μm)

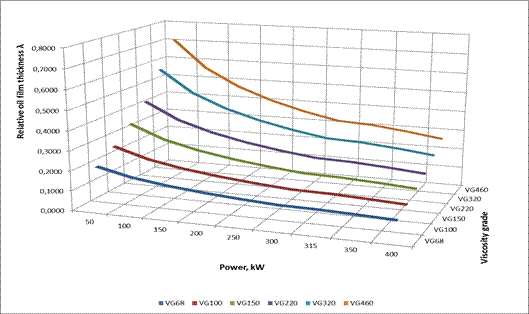
Fig. 5. Plots of the relative oil film thickness λ at Point B of the engagement section as a function of the power of the driving motor and the viscosity grade (the results obtained for
Ra=0.4 μm)

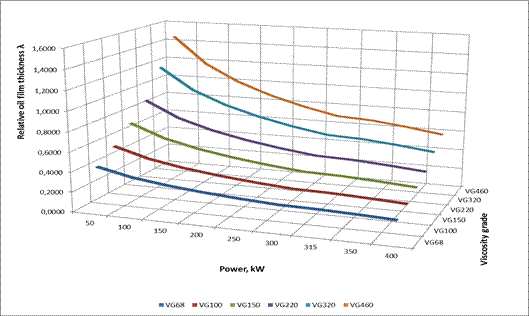
Fig. 6. Plots of the relative oil film thickness λ at Point B of the engagement section as a function of the power of the driving motor and the viscosity grade (the results obtained for
Ra=1 μm)

4. SUMMARY

Around the world, research is being carried out to improve the durability and reliability of machine parts [7-22].

As a part of this study, the lubrication conditions of a typical mining gearbox used in drives of longwall armoured face conveyors were determined using a modified calculation method based on the ISO/TR 15144-1:2014 (E) standard. The spur gear stage of a KPL-25 gearbox with the gear ratio i=39 was subjected to analysis. The values of the relative oil film thickness λ were determined as a function of the position on the engagement section. Based on the plot, it has been found that the smallest values of the parameter λ are at the single-tooth engagement point (Point B) on the engagement section.

For single-tooth engagement Point B on the engagement section, the values of the relative oil film thickness λ were determined as a function of load, oil viscosity grade and roughness.

The scope of the analytical work carried out allowed for the following conclusion to be made: the gearbox under consideration operates unfavourable conditions of boundary lubrication; only in some cases is it possible to create mixed lubrication conditions.

Based on the data presented, it is also possible to formulate a general recommendation to take into account the operating conditions of gearboxes at the design stage and select appropriate technological means, which ensure the best-possible lubrication conditions.

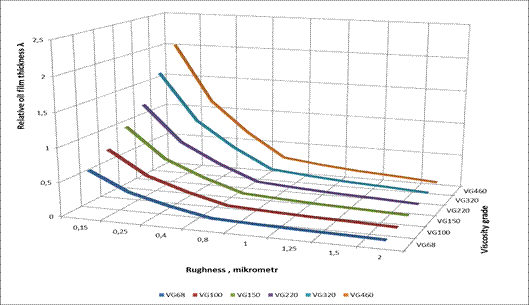
Fig. 7. Plots of the relative oil film thickness λ at Point B of the engagement section as a function of the roughness and the viscosity grade (the results obtained for power P=315 kW)

References

1. Skoć Antoni, Jacek Spałek, Sylwester Markusik. 2014. Basics of Machine Construction. Vol. II. Warsaw: WNT. ISBN 978-83-2043-405-7.

2. Lawrowski Zbigniew. 1996. Lubrication Technology. Warsaw: PWN. ISBN 978-830-1074-890.

3. Dowson D., G.R. Higginson. 1976. Elastohydrodynamic Lubrication. Oxford, London: Pergamon Press. ISBN 978-148-318-1899.

4. Hamrock B.J., D. Dowson. Ball Bearing Lubrication. 1981. New York, Chichester, Brisbane, Toronto, Singapore: John Wiley & Sons. ISBN 978-047-1035-534.

5. Wiśniewski M. Elastohydrodynamic Lubrication. 2000. Renningen-Malmsheim: Expert Verlag. ISBN 978-3-8169-1745-8.

6. ISO/TR 15144-1:2014 (E) Calculation of Micropitting Load Capacity Of Cylindrical Spur And Helical Gears – Part 1: Introduction and Basic Principles.

7. Bigoš P., J. Kuľka, M. Mantič, M. Kopas. 2015. “Comparison of local stress values obtained by two measuring methods on blast furnace shell”. Metalurgija 54(1): 101-104.

8. Czech P. 2013. “Intelligent Approach to Valve Clearance Diagnostic in Cars”. Activities of Transport Telematics. TST 2013. Communications in Computer and Information Science 395: 384-391. DOI: https://doi.org/10.1007/978-3-642-41647-7_47.

9. Czech P., Mikulski J. 2014. “Application of Bayes Classifier and Entropy of Vibration Signals to Diagnose Damage of Head Gasket in Internal Combustion Engine of a Car”. Telematics - Support For Transport. TST 2014. Communications in Computer and Information Science 471: 225-232. DOI: https://doi.org/10.1007/978-3-662-45317-9_24.

10. Figlus T., J. Gnap, T. Skrucany, B. Sarkan, J. Stoklosa. 2016. “The Use of Denoising and Analysis of the Acoustic Signal Entropy in Diagnosing Engine Valve Clearance”. Entropy 18(7): 1-11. DOI: https://doi.org/10.3390/e18070253.

11. Figlus T., S. Liscak. 2014. “Assessment of the vibroactivity level of SI engines in stationary and non-stationary operating conditions”. Journal of Vibroengineering 16(3): 1349-1359.

12. Grega R., J. Homisin, M. Puskar, J. KuI’ka, J. Petroci, B. Konecny, B. Krsak. 2015. “The chances for reduction of vibrations in mechanical. System with low-emission ships combustion engines”. International Journal of Maritime Engineering 157(A4): 235-240. DOI: 10.3940/rina.ijme.2015.a4.335.

13. Harachová D. 2016 “Deformation of the elastic wheel harmonic gearing and its effect on toothing”. Grant Journal Vol. 5, No. 1: 89-92, ISSN: 1805-0638.

14. Homišin J., P. Kaššay, M. Puškár, R. Grega, J. Krajňák, M. Urbanský, M. Moravič. 2016. “Continuous tuning of ship propulsion system by means of pneumatic tuner of torsional oscillation”. International Journal of Maritime Engineering: Transactions of the Royal Institution of Naval Architects 158(A3): 231-238. ISSN: 1479-8751. DOI: 10.3940/rina.ijme.2016.a3.378.

15. Krajnák J., J. Homišin, R. Grega, M. Urbanský. 2016. “The analysis of the impact of vibrations on noisiness of the mechanical system”. Diagnostyka 17(3): 21-26.

16. Kulka J., E. Faltinová, M. Kopas, M. Mantič. 2016. “Diagnostics and optimisation of crane track durability in metallurgical plant”. Diagnostyka 17(3): 41-46.

17. Medvecká-Beňová S. L. Miková, P. Kaššay. 2015. “Material properties of rubber-cord flexible element of pneumatic flexible coupling”. Metalurgija 54(1): 194-196.

18. Puskar Michal, Michal Fabian, Jaroslava Kadarova, Peter Blist’an, Melichar Kopas. 2017. “Autonomous vehicle with internal combustion drive based on the homogeneous charge compression ignition technology”. International Journal of Advanced Robotic Systems 14(5). DOI: 10.1177/1729881417736896.

19. Puskar Michal, Melichar Kopas, Jaroslava Kadarova. 2017. “Ecological analysis related to creation of gaseous emissions within transport focused on fulfilment of the future emission standards”. Transportation Research Part D: Transport and Environment 57: 413-421. DOI: 10.1016/j.trd.2017.10.007.

20. Vojtková Jarmila. 2016. “Benefits of application of spur gears with asymmetric profile”. Pomiary Automatyka Robotyka 2(20): 31-35. DOI: 10.14313/PAR_220/31.

21. Zelić A., N. Zuber, R. Šostakov. 2018. “Experimental determination of lateral forces caused by bridge crane skewing during travelling”. Eksploatacja i Niezawodnosc – Maintenance and Reliability 20(1): 90-99. DOI: http://dx.doi.org/10.17531/ein.2018.1.12. ISSN: 1507-2711.

22. Zuber N., R. Bajrić. “Application of artificial neural networks and principal component analysis on vibration signals for automated fault classification of roller element bearings”. Eksploatacja i Niezawodność - Maintenance and Reliability 18(2): 299-306. DOI: 10.17531/ein.2016.2.19. ISSN: 1507-2711.

Received 05.11.2017; accepted in revised form 09.01.2018

Scientific Journal of Silesian University of Technology. Series Transport is licensed under a Creative Commons Attribution 4.0 International License

[1] Faculty of Mining and Geology, Silesian University of Technology, Akademicka 2 Street, 44-100 Gliwice, Poland. E-mail: andrzej.n.wieczorekk@polsl.pl.