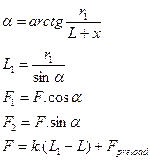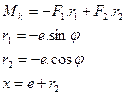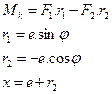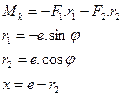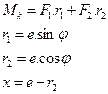Article citation information:

Urbanský, M. Harmonic analysis of torsional vibration force excitation. Scientific Journal of Silesian University of Technology. Series Transport. 2017, 97, 181-187. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2017.97.16.

 

 

Matej URBANSKÝ[1]

 

 

 

HARMONIC ANALYSIS OF TORSIONAL VIBRATION FORCE EXCITATION

 

Summary. In our department, we deal with various methods for the continuous tuning of torsional oscillating mechanical systems during their operation, mainly in terms of torsional vibration magnitude. Therefore, in order to carry out necessary experimental research, we need torsional oscillation exciters, which operate on various principles. The objective of this paper is to conduct a harmonic analysis of a torsional oscillation force excitation mechanism, in order to identify the possibilities of its application.

Keywords: torsional vibration; force excitation; harmonic analysis

 

 

1. INTRODUCTION

 

In the laboratory of our workplace (namely, the Department of Construction, Automotive and Transport Engineering), we are involved in the measuring and tuning of torsional oscillation in torsional oscillating mechanical systems (TOMSs).

In terms of dynamics, it is possible to define a TOMS (Fig. 1) as a mass disk system. These disks are connected together with flexible bonds, wherein rotary power transmission occurs, with torsional beats and vibration arising during operation [1-6,8-10,12]. Their intensity depends on the dynamic terms of the respective mechanical system (mainly on natural frequency and torsional excitation source).

 

NHM

 

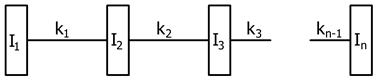
Fig. 1. Torsional oscillating mechanical system

 

The most dangerous torsional vibration is caused by devices that are working with time-variable periodic torque, e.g., [1,2,5-10,13,15,16]:

 

·                     Piston machines (combustion engines, compressors)

·                     Gear transmissions and cam mechanisms

·                     Propellers (of ships, fans etc.)

 

The system reaches the most critical torsional vibration values in the resonance area when the mechanical system’s natural frequency is equal to the excitation frequency. The resonance is much higher when loading the mechanical system’s parts.

In our department, we deal with the continuous tuning of TOMSs during their operation (see [8-10,12]). This continuous tuning mainly concerns the magnitude of torsional vibrations (but also the magnitude of rectilinear vibrations or noise arising from torsional vibrations). For this continuous tuning, we use pneumatic flexible shaft couplings (pneumatic torsional vibration tuners) developed by our department (see [11,14]).

The torsional stiffness of the given pneumatic tuners, and in turn the natural frequencies of the torsional systems, can be changed by adjusting the gaseous media (most commonly, air) pressure in their pneumatic flexible elements. With a suitable value of torsional stiffness k (k2 < k1 < k3), resonances from individual harmonic components of excitation (Fig. 2) can be moved from the operational speed (n) range (OSR) of the mechanical system, and herewith the value of dynamic component MD of the transmitted load torque can be reduced, i.e., [6,8-10,12,15].

 

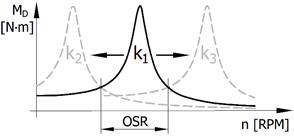
Princíp ladenia mechanických sústav

 

Fig. 2. Mechanical system’s tuning principle

 

In our laboratory, in order to carry out our complex research practice, we need torsional oscillation exciters, which operate on various principles, in addition to torsional oscillation tuners. The objective of this paper is to perform a harmonic analysis of a special torsional oscillation force excitation mechanism, in order to identify the possibilities of its application.

 

 

2. force torsional oscillation excitation mechanism

 

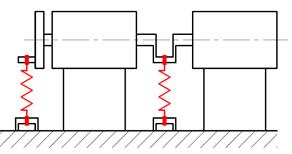
The mechanism for force torsional oscillation excitation, as shown in Figure 3, produces, during its operation, the load torque of an alternating character. The force of the extended tension spring (1) and arm depends on the turn angle of the rotary flange, on which the excentre is (4) mounted. To avoid damage to the spring eyes during operation of the mechanism (as a consequence of frictional wear), it is necessary to use bearings in places (2) and (3). It is possible to adjust the spring preload by a spring extension fixed to the base plate (5). As we can see in Figure 3b, this mechanism can be mounted:

·                       to the frontal surface of the driving or driven machine flange

·                       to the crank of the crankshaft situated in the drive chain of a mechanical system

 

 

Pružinové budenie_menší

Mechanizmus

a)

b)

 

Fig. 3. Force torsional oscillation excitation mechanism: a) construction example and b) application scheme

 

 

3. Derivation of mathematic formulas for force excitation

 

In Figure 4, a schematic drawing of the given mechanism with force terms is presented.

 

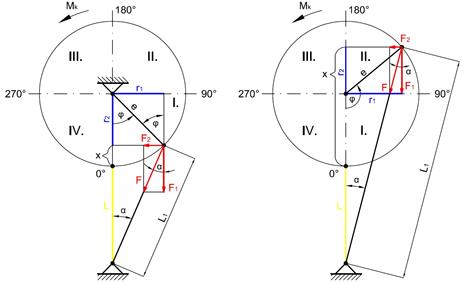
Pružinové budenie

 

Fig. 4. Mechanism scheme with force terms

 

Consequently, as shown in Table 1, formulas are derived for torque Mk from Figure 4, where: Mk - torque, which it is necessary to expend on rotation in the direction of rotation angle φ, which increases counterclockwise; F         - spring force, which is decomposed to components F1 and F2; L - distance of the axes of the spring grip pins in the bottom dead centre.

 

Tab. 1

Derived formulas for torque Mk

 

All quadrants

 Quadrant III

Quadrant II

Quadrant IV

Quadrant I

 

 

4. HARMONIC ANALYSIS OF the EXCITATION

 

In Table 2, the amplitude values of the first, second and third harmonic components (HCs) and the various eccentricity values of the phase angle without a spring preload are computed. The amplitudes of higher HCs have only a negligible size (less than 1% of the first HC amplitude).

Tab. 2

Computed values of harmonic components without spring preload

Eccentricity

[% of L]

1st HC amplitude MA1 [N.m]

(MA2/MA1).100

[%]

(MA3/MA1).100

[%]

2nd HC phase angle shifting ψ2 [°]

3rd HC phase angle shifting ψ3 [°]

L [m]

1

0.040.x

49.443

0.367

180.5

181

Constant

5

x

47.324

1.700

180.5

181

Constant

10

4.019.x

44.896

3.060

180.5

181

Constant

15

9.076.x

42.686

4.171

180.5

181

Constant

20

16.187.x

40.668

5.075

180.5

181

Constant

25

23.359.x

38.817

5.808

180.5

181

Constant

50

102.238.x

31.503

7.818

180.5

181

Constant

 

In Table 3, the amplitude values of the first, second and third harmonic component (HCs) involving various spring preloads with a constant eccentricity value of 10% of L are computed. The value of ψ2, in all cases, is 180.5°, while the value of ψ3, in all cases, is 181°.

 

Tab. 3

Computed values of harmonic components with spring preload

 

Eccentricity

[% of L]

1st HC amplitude MA1 [N.m]

(MA2/MA1).100

[%]

(MA3/MA1).100

[%]

Spring preload

[stretched % of L]

L [m]

10

x

44.896

3.060

0

Constant

10

1.494.x

28.541

1.945

5

Constant

10

1.990.x

20.318

1.385

10

Constant

10

2.483.x

15.369

1.047

15

Constant

10

2.977.x

12.063

0.822

20

Constant

10

3.472.x

9.699

0.661

25

Constant

10

3.966.x

7.924

0.540

30

Constant

10

4.461.x

6.542

0.446

35

Constant

10

4.955.x

5.437

0.370

40

Constant

 

It is possible to describe the dependence of load torque Mk, which arises during the operation of the given mechanism, on rotation angle φ using the following formula:

 

Mk = MA1.sin φ + MA2 sin (2.φ + ψ2) + MA3 sin (3.φ + ψ3),

 

where: MA1, MA2, MA3 - amplitudes of the first, second and third HCs of excitation; Ψ2 and Ψ3 - phase angle shifting of these second and third HCs towards the first HC.

 

5. CONCLUSION

 

From the values stated in Tables 2 and 3, it is possible to say that:

 

·           Without a spring preload, but with a linearly increasing eccentricity percentage value, the first HC amplitude value increases quadratically, the second HC amplitude percentage decreases and the third HC percentage increases.

·           With a suitable spring preload, we can increase the first HC amplitude value, substantially reduce the second HC amplitude value and minimize the third HC amplitude value to a negligible size (less than 1% of the first HC amplitude).

 

These facts relate to the property of the given mechanism (not its deficiency). Among general advantages of the mechanism, it is possible to mention:

 

·           Negligible small friction resistances while operational

·           Simplicity of its construction and therefore low manufacturing costs

·           Simple and accurate calculation of load torque dependence

 

The main disadvantage of the given mechanism is the rise of relatively high radial loading in the system at the point of the excentre in relation to the rotary part mounting, which should be provided at the shafts, and the dimension of the bearings.

 

 

References

 

1.             Czech P., J. Mikulski. 2014. “Application of Bayes Classifier and Entropy of Vibration Signals to Diagnose Damage of Head Gasket in Internal Combustion Engine of a Car”. In: J. Mikulski (ed.). 14th International Conference on Transport Systems Telematics. Katowice Ustron, Poland. 22-25 October 2014. Telematics - Support for Transport. Book series: Communications in Computer and Information Science, Vol. 471: 225-232.

2.             Czech P. 2013. “Intelligent approach to valve clearance diagnostic in cars”. In: J. Mikulski (ed.). 13th International Conference on Transport Systems Telematics. Katowice Ustron, Poland. 23-26 October 2013. Activities of Transport Telematics. Book series: Communications in Computer and Information Science, Vol. 395: 384-391.

3.             Figlus Tomasz, Marcin Stańczyk. 2016. “A method for detecting damage to rolling bearings in toothed gears of processing lines”. Metalurgija 55(1): 75-78. ISSN: 0543-5846.

4.             Figlus Tomasz, Marcin Stańczyk. 2014. “Diagnosis of the wear of gears in the gearbox using the wavelet packet transform”. Metalurgija 53(4): 673-676. ISSN: 0543-5846.

5.             Folega Piotr, Grzegorz Wojnar, Rafał Burdzik, Łukasz Konieczny. 2014. “Dynamic model of a harmonic drive in a toothed gear transmission system”. Journal of Vibroengineering 16 (6): 3096-3104. ISSN 1392-8716.

6.             Fraunhofer L.B.F. 2015. Gesteigerter Yacht-Genuss: Aktive Kupplung mindert Schwingungen in Schiffsantrieben. [In German: Increased Yacht Enjoyment: Active Clutch Reduces Vibration in Ship Propulsion Systems.] Available at: http://www.lbf.fraunhofer.de.

7.             Gąska Damian, Tomasz Haniszewski, Jerzy Margielewicz. 2017. “I-beam girders dimensioning with numerical modelling of local stresses in wheel-supporting flanges”. Mechanika 23(3): 347-352. ISSN 1392-1207.

8.             Homišin Jaroslav. 2002. Nové typy pružných hriadeľových spojok: Vývoj-Výskum-Aplikácia. [In Slovak: New Types of Flexible Shaft Couplings: Development-Research-Application.] Košice: Vienala. ISBN 80-7099-834-2.

9.             Homišin Jaroslav. 2006. “Tuning methods of mechanical systems by means of torsional oscillation tuner application”. Pneumatyka 61 (6): 32-35. ISSN 1426-6644.

10.         Homišin Jaroslav, Peter Kaššay. 2014. “Experimental verification of the possibility using pneumatic flexible shaft couplings for the extremal control of torsional oscillating mechanical system”. Diagnostyka 15 (2): 7-12. ISSN 1641-6414.

11.         Kaššay Peter. 2017. Pneumatická pružná hriadeľová spojka s hadicovým pružným elementom. [In Slovak: Pneumatic Flexible Shaft Coupling with Hose-resilient Element.] Utility pattern SK 7708 Y1. Banská Bystrica: ÚPV SR 2017.

12.         Lacko Pavol. 1988. “Die kontinuierliche Änderung dynamischer Parameter von Schwingungssystemen im Betriebszustand”. [In German: “The continuous change of dynamic parameters of vibration systems in the operating state.”] Maschinenbautechnik 6: 274-277.

13.         Mario De Luca. 2017. ”A comparison between prediction power of artificial neural networks and multivariate analysis in road safety management”. Transport 32(4): 379-385. ISSN: 1648-4142. DOI: https://doi.org/10.3846/16484142.2014.995702.

14.         Patent PL 216901 B1. Układ mechaniczny strojony w sposób płynny. [In Polish: Mechanical System Tuned in a Smooth Way.] Homišin J., 2014.

15.         Sapieta M., A. Sapietová, V. Dekýš. 2017. “Comparison of the thermoelastic phenomenon expressions in stainless steels during cyclic loading”. Metalurgija 56 (1-2): 203-206. ISSN 0543-5846.

16.         Wittek Adam Marek, Damian Gąska, Bogusław Łazarz, Tomasz Matyja. 2014. “Automotive stabilizer bar – stabilizer bar strength calculations using FEM, ovalization of radial areas of tubular stabilizer bars”. Mechanika 20(6): 535-542. ISSN 1392-1207.

 

 

This paper was written within the framework of the KEGA 041TUKE-4/2017 grant project entitled, Implementation of New Technologies Specified for Solving Questions Concerning the Emissions of Vehicles and Their Transformation in Educational Processes in Order to Improve the Quality of Education.

 

This article was created with support from the PhD students and young researchers project entitled, Solution of a Control System Element for Mechanical Systems’ Continuous Tuning.

 

 

Received 19.08.2017; accepted in revised form 01.11.2017

 

Scientific Journal of Silesian University of Technology. Series Transport is licensed under a Creative Commons Attribution 4.0 International License


[1] Faculty of Mechanical Engineering, Department of Construction, Automotive and Transport Engineering Technical University of Košice, Letná 9 Street, 042 00 Košice, Slovakia. E-mail: matej.urbansky@tuke.sk.