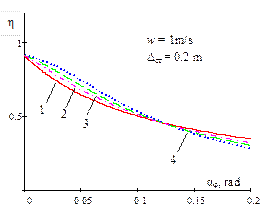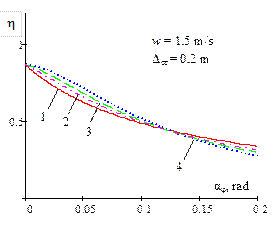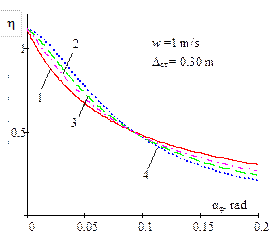Article citation information:
Lyashuk, О., Sokil, M., Vovk, Y., Tson,
O., Dzyura, V. The impact of the kinematic parameters of bounce and pitch
motions of sprung mass on wheeled vehicles handling. Scientific Journal of Silesian University of Technology. Series
Transport. 2017, 97, 81-91.
ISSN: 0209-3324. DOI:
https://doi.org/10.20858/sjsutst.2017.97.8.
Оleg LYASHUK[1],
Mariya SOKIL[2],
Yuriy VOVK[3],
Oleg TSON[4],
Volodymyr DZYURA[5]
THE
IMPACT OF THE KINEMATIC PARAMETERS OF BOUNCE AND PITCH MOTIONS OF SPRUNG MASS
ON WHEELED VEHICLES HANDLING
Summary. The
impact of the kinematic parameters of bounce and pitch motions of wheeled
vehicles’ (WVs’) sprung mass (SM) with non-linear power characteristics of the
cushion system on vehicles handling is studied. The dependence of the critical
value of the dynamic steering angle of directive wheels on the amplitude of
bounce and pitch motions and the kinematic parameters of motion is developed.
It is proven that the limit value of the dynamic steering angle of directive wheels
is reduced during acceleration, and vice versa (it increases during braking,
while the bounce and pitch motions are significantly reduced).
Keywords: wheeled vehicles handling;
directive wheels; amplitude; frequency; steering angle
1. INTRODUCTION
The
handling of a WV describes the ability of a driver to change the direction of a
car and steer it using a steering wheel [1]. Consequently, an angle between the
vector of the WV speed and the plane of directive wheels is changed. The
steering torque is the main factor of car handling. Loads on a tyre and the
interaction of the tyre with road pavements etc. define the steering torque. In
the case of steady movement along a horizontal road without surface
irregularities, these factors are considered invariable. Therefore, the limit
value of the steering angle control is invariable. However, during unsteady
movement (accelerated or damped) and WV movement along a road with surface
irregularities, dynamic load on the tyre is a variable value. This dynamic load
significantly changes the limit value of the steering angle control. In
addition, the SM motions depend on the power characteristics of the cushion system (CS) and the dynamic load
constituent. Thus, the issue of car handling should be considered, taking into
account both external and internal factors. Such issues are the subject of this
work. In addition, to study the impact of the dynamics of WVs’ SM on the limit
value of the steering angle control, the non-linear relation of CS elastic
power characteristics was developed [2].
2. MATERIALS AND METHODS
Based on a two-dimensional analytical model, the set task can be solved (Fig. 1). For this model:
- The WV moves along the straight line with acceleration w.
- The
centre of the SM is in point O, which is defined by parameters 
; P,P1, P2.
- Correspondingly, the weight of the SM, the front and rear axles is determined.
- The
suspension system is characterized by elastic forces and drag forces, which are
defined by dependencies [2-4] 
, 
, where 
are steels, 
and 
.
- Correspondingly,
this leads to the deformation of elastic shock absorbers and their speed (
for the front suspension and 
for the rear suspension).
- The
deformation of tyres caused by WV collision with surface irregularities is a
small value compared to the deformation of elastic shock absorbers; and it
would be neglected when solving the task. Surface irregularities of the road
pavement cause small SM motions around the centre O, while its relative
position is uniquely determined by parameter 
.
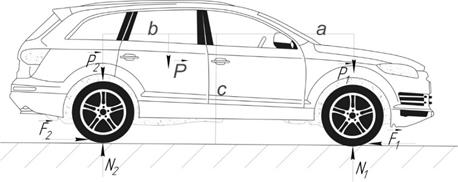
Fig. 1. Analytical
model and distribution of external forces acting on a WV
As emphasized above, the limit value of the dynamic steering angle control is largely determined by the pressure forces of the ‘unsprung mass-sprung mass’ system on a road pavement, i.e., by the value of dynamic reaction N1. The latter is largely determined by the law of the SM’s relative motion. To describe this law, the differential equation of the SM’s relative motion is deduced. If the motion is rotary around the SM centre, the following equation applies:
(1)
where: 
- moment of
inertia of sprung mass relative to the centre of mass; 
- given driving and
drag forces; 
- moment of inertia of
sprung mass relative to the point О. In this work, SM is considered
symmetrical relative to the longitudinal axis passing through the centre of
mass, therefore 
Based on the accepted
hypotheses concerning CS power characteristics, the differential equation (1)
is deduced:
(2)
The problem of developing its exact solution is unsolved. However, the restrictions imposed above the system allow for general ideas of perturbation methods to be applied in order to solve the equation [6,7]. The perturbation methods’ effectiveness largely depends on the development of a solution for the unperturbed analogue in Equation (3); in particular:
(3)
Equations
(5) and (6) will describe the sprung part (SP) motions, if the relation 
, (
) defines the parameter v +
(4)
where 
, 
; correspondingly, the amplitude and
frequency of the natural bounce and pitch motions of SP, 
represent the motions phase. If the rigidity parameters of the
elastic shock absorbers of the WV’s CS 
, 
are connected by the relation 
(
- known constant), the notion of the
static deformation of elastic shock absorbers 
can be more reasonably applied. In this case,
the frequency of natural motions can be changed by a dependence that is more
convenient. Therefore, 
and the frequency of natural motions can be presented
as:
(5)
For the
unperturbed Equation (6), parameters 
are constant, as a proper system is
conservative. The analytical approximation of the impact of drag forces and
other non-linear forces is presented on the right-hand side of Equation (5).
This impact occurs in motion damping and, consequently, in the change in damped
motion frequency. Based on the Van der Pol method [7] and the specified
system, the impact of the given forces can be easily defined. According to this
method’s basic idea, the first asymptotic approximation that describes the
bounce and pitch motions of SP, with consideration given to drag forces, is
represented as:
(6)
where: 
and 
are variables in time functions, whose laws of
change are determined by the right-hand side of Equation (4) [8].
(7)
where: 
- semi-period of the applied periodic Ateb
functions, in particular
.
The dynamic pressure forces of the front wheels on the road pavement can be determined by applying the law of SM motion. In conformity with the D’Alembert [5] principle for the ‘unSP-SP’ mechanical system, the following equations are deduced:
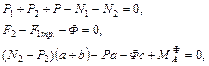(8)
where: 
, 
-weight of the rear (drive) and the front
axles, respectively; 
- driving force and the drag force; 
,
- normal constituents of road
reactions; 
- WV inertia force, 
- inertia force moment of the SM
relative to the contact point of a directive wheel and road pavement (point A).
Further, in this work, in order to determine the dynamic value of WV pressure
forces on the supporting surface, the extreme values of SP inertia forces are
applied, that is:
(9)
where: 
- the moment of inertia of a SP
relative to the contact point of a directive wheel with the road. According to
the Huygens and Steiner theorem [4], this equals:
.
Based on the third equation in (9), an unknown force intensity of the road pavement interacting with the tractive wheel can be identified:
(10)
as well as the extreme value of directive wheels’ pressure force on the road pavement:
(11)
where: 
- the directive wheels’ pressure force on the road pavement. The
developed analytical Equation (11) allows for defining the SM static
deformations 
:
(12)
The
developed dependences allow for determining the angular stiffness of tyre 
relative to the vertical axis 
, with the empirical relationship
determining coefficient 
. All the above-mentioned allows for
determining the moment of dynamic cornering resistance for tyres, if the latter
is proportional to the steering angle of the tyre:
(13)
where: 
- the steering angle of a directive wheel relative to the kingpin (a
wheel turns relative to this axis).
3. RESULTS AND DISCUSSION
The
steering condition of the WV (with consideration given to the SP motions and a
variable speed of movement 
) takes the form 
, where: 
- limit value for the adherence of tyre
cornering resistance, which occurs at full sliding of tyres elements in contact
with the road pavement [1]. The maximum value of the static moment of tyre cornering
resistance can be defined from the dependence 
, where: 
- the limit value of a directive
wheel’s steering angle. This value is defined empirically for different types
of road pavements. In this case, in order to define the limit for the steering
angle of a directive wheel, with consideration to the SP pitch motions, the
following dependence is developed:
(14)
Considering
the resulting relation, the value of the critical dynamic steering angle 
is developed in terms of the dependence on the
amplitude of the bounce and pitch motions of the SP, the speeding WV and the
parameters that describe the power characteristics of the SM:
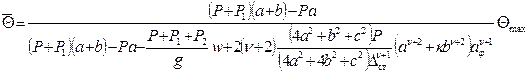(15)
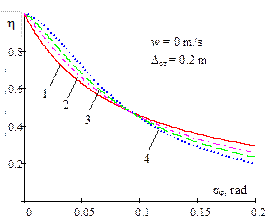
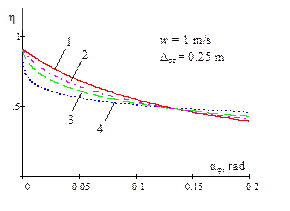
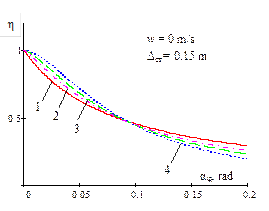
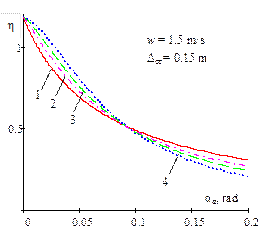
Fig. 2
shows the dependence of the interrelation of the critical value of the dynamic
steering angle on its static value (
) for different parameters of the
power suspension of the accelerating WV, if w=0; 1; 1.5.
4. CONCLUSIONS
Based
on the obtained results and the developed graphic dependencies, the following
conclusions can be made:
- First,
according to the non-linear law of changing the restoring force of the CS, the natural
frequency of the bounce and pitch motions depend on the amplitude. In addition,
the greater the amplitude value, the greater the value of the natural frequency
of motions.
- Second,
the CS’ bounce and pitch motions greatly reduce the critical (limit) angle
value. The greater the values of the amplitude of the studied motions, the
smaller the critical steering angle.
- Third, the time shift of the WV speed changes
the critical steering angle value. The accelerated motion (for all other
similar parameters) corresponds to a smaller value for the dynamic steering
angle and vice versa, i.e., the damped motion corresponds to a greater value
for the critical steering angle.
|
1- |
1- |
|
1- |
1 - |
|
1 - |
1 - |
|
Fig. 2. Dependence of the
interrelation of the critical value of the dynamic steering angle, with
regard to a static value of the same magnitude, on the amplitude of the
bounce and pitch motions for different power parameters of progressive
non-linear vehicle suspension and acceleration (w = 0; 1; 1.5) |
|
; 2-
; 3- 
; 4-
|
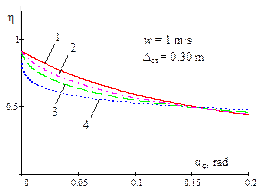
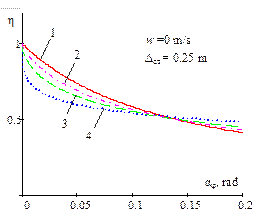
1 - |
1 - |
||
|
1 - |
1 - |
||
|
1 - |
1 - |
||
|
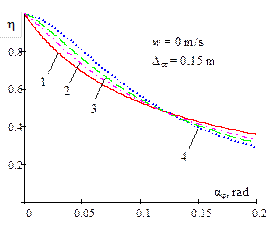
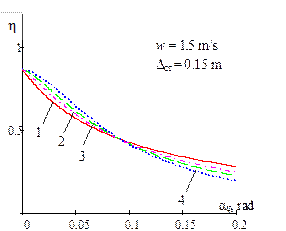
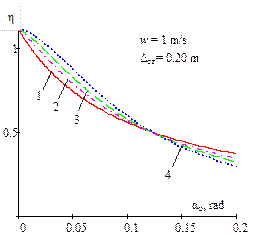
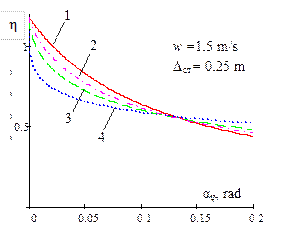
Fig. 3. Dependence of the ratio of
the critical value of the dynamic steering angle, with regard to a static
value of the same magnitude, on the amplitude of bounce and pitch motions for
different power parameters of non-linear regressive vehicle suspension and
acceleration (w = 0; 1; 1.5) |
|||
|
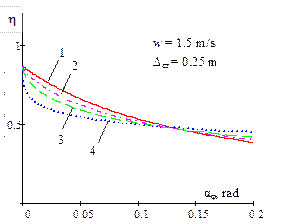
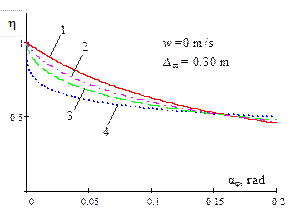
1 - |
1 - |
||
|
1 - |
1 - |
||
|
1 - |
1 - |
||
|
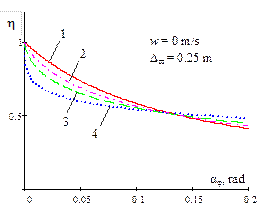
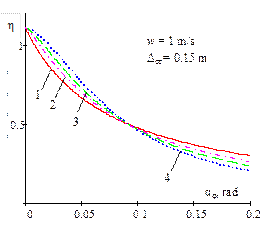
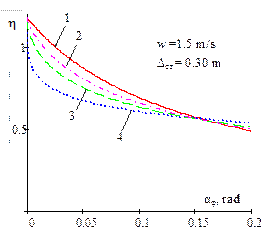
Fig. 4. Dependence of the ratio
of the critical value of dynamic steering angle, with regard to a static
value of the same magnitude, on the amplitude of the bounce and pitch motions
for different power parameters of non-linear progressive vehicle suspension
and damping |
|||
|
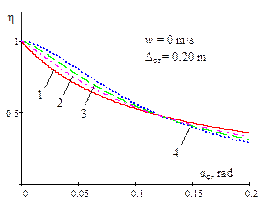
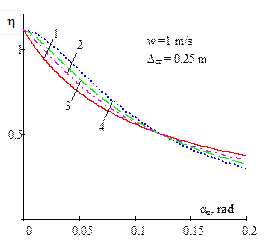
1 - |
1 - |
||
|
1 - |
1 - |
||
|
1 - |
1 - |
||
; 3- 
; 4-
; 3- 
; 4-
; 3- 
; 4-
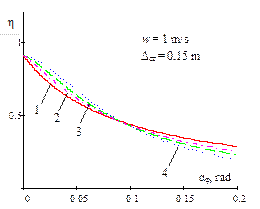
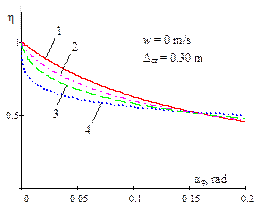
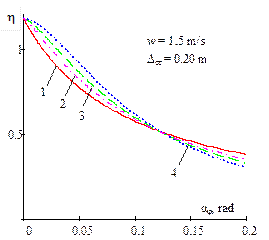
Fig. 5. Dependence of the ratio of
the critical value of dynamic steering angle, with regard to the static value
of the same magnitude, on the amplitude of the bounce and pitch motions for
different power parameters of non-linear progressive vehicle suspension and
damping
(w = 0; 1; 1.5)
References
1. Солтус А.П. 2010. Теорія експлуатаційних властивостей автомобіля: Навчальний посібник для ВНЗ. [In Ukrainian: Soltus А.P. 2010. The Theory of Operational Properties of the Vehicle: Textbook for Universities.] Kiev: Aristey.
2. Грубель М.Г. 2014. “Вплив відновлювальної сили пружної підвіски на коливання та стійкість руху колісних транспортних засобів”. Перспективи розвитку озброєння і військової техніки СВ: тези доповідей Міжнародної НТК: 35. Львів: ACB. [In Ukrainian: Hrubel’ М.H. 2014. “Effect of elastic suspension of renewable power on fluctuations and resistance movement of wheeled vehicles”. Prospects for the Development of Arms and Military Equipment JI: Reports of the International NTC: 35.] Lviv: ASV.
3. Грубель М.Г., О.П. Красюк, М.Б. Сокіл, Р.А. Нанівський. 2014. “Вертикальні коливання підресореної частини колісних транспортних засобів під дією випадкових збурень”. [In Ukrainian: Hrubel’ М.H., O.P. Krasiuk, R.A. Nanivs’kyi, M.B. Sokil. 2014. “The vertical oscillations of the sprung motor vehicles under the influence of random disturbances”.] Scientific Notes of NTC 46: 112-116.
4. Кузьо І. В., Сокіл Б. І., Палюх В. М. 2007. “Вплив параметрів підвіски на нелінійні коливання транспортних засобів”. [In Ukrainian: Kuzio І.V. 2007. “Effect of suspension parameters on non-linear oscillations of vehicles.”] Bulletin of NU “LP” Dynamics, Strength and Design of Machines and Devices 588: 49-52.
5. Айзерман М.А. 1980. Классическая механика. [In Russian: Aizerman М.А. 1980. Classical Mechanics.] Moscow: Nauka.
6. Коул Д. 1972. Методы возмущений в прикладной математике. [In Russian: Coul J. 1972. Perturbation Methods in Applied Mathematics.] Moscow: Mir.
7. Боголюбов Н.Н., A. Митропольский Ю. 1974. Асимптотические методы в теории нелинейных колебаний. [In Russian: Boholiubov N.N., A. Mytripol’skyi. 1974. Asymptotic Methods in the Theory of Non-linear Oscillations.] Moscow: Nauka.
8. Сеник П. М. 1969. “Обернення неповної Вeta-функцiї”. [In Ukrainian: Senyk P.М. 1969. “Rotation of incomplete beta-function”.] Ukrainian Mathematics Journal 21 (3): 325-333.
9. Сеник П. М., Б.І. Сокіл. 1977. “Про застосування u-методики для одного класу коливних систем”. [In Ukrainian: Senyk P.М., B.I. Sokil. 1977. “On applying the u-technique for one class of vibration systems”.] Rep. of АS of USSR 1: 12-16.
10. Сеник П. М., Б.І. Сокіл. 1977. “Об определении параметров нелинейной колебательной системы по амплитудно-частотной характеристике”. [In Russian: Senyk P.М. 1977. “On determining the parameters of non-linear vibrational system according to amplitude and frequency characteristics.”] Mathematical Methods and Physicomechanical Fields 7: 94-99.
Received 05.09.2017; accepted in revised form 02.11.2017
Scientific Journal of Silesian
University of Technology. Series Transport is licensed under a Creative
Commons Attribution 4.0 International License