Article citation information:
Homišin, J. Optimal tuning of mechanical
systems by application of a pneumatic tuner of torsional oscillation. Scientific Journal of Silesian University of
Technology. Series Transport. 2017, 97,
47-55. ISSN: 0209-3324. DOI:
https://doi.org/10.20858/sjsutst.2017.97.5.
Jaroslav HOMIŠIN[1]
OPTIMAL
TUNING OF MECHANICAL SYSTEMS BY APPLICATION OF A PNEUMATIC TUNER OF TORSIONAL
OSCILLATION
Summary. Reducing
the dynamic load of any mechanical system can be achieved when the torsional
vibration magnitude is optimized by applying a pneumatic tuner of torsional
oscillation. Changing the torsional stiffness of a pneumatic tuner can be
accomplished by changing the pressure of the gaseous medium, out of operation
or during the operation of a mechanical system. This results in two suggested
methods of tuning: (i) tuning of torsional
oscillating mechanical systems that are out of operation, which fulfils the
conditions for mechanical system tuning; (2) tuning mechanical systems during
an operation in a steady state, thus ensuring the conditions of so-called
continuous tuning of the given systems. The aim of this paper is to present the
possibility of controlling torsional oscillation of a mechanical system that is
out of operation by applying a tangential pneumatic tuner of torsional
oscillation.
Keywords: mechanical system; torsional vibration of mechanical systems; pneumatic
tuner of torsional oscillation; tuning of mechanical system
1. INTRODUCTION
Reducing the dynamic load of
individual parts of any mechanical system is achieved by optimal tuning, i.e.,
optimizing the system in terms of the magnitude of torsional oscillation. The
most preferred member for tuning any mechanical system in advance is a suitably
adapted pneumatic tuner of torsional oscillation. In our department, among
others, we have been engaged in the development and research of pneumatic
tuners of torsional oscillation for a long time. In particular, we focus on the
possibilities of applying the given tuners of torsional oscillating mechanical
systems with the intention to optimize them in terms of minimizing or
eliminating dangerous torsional vibrations.
The aim of this
paper is to present the possibility of controlling the torsional oscillation of
mechanical systems that are out of operation by applying a tangential
pneumatic tuner of torsional oscillation.
2. BRIEF
characteristics of pneumatic tuners of Torsional Oscillation
2.1. Tangential pneumatic tuner of torsional
oscillation
Tangential pneumatic tuning of torsional oscillation (Fig. 1a-b) consists of a driving (1) and a driven part (2)
between which a compression space is located. The compression space is formed
by circumferentially and tangentially spaced pneumatic-flexible elements (3). The pneumatic-flexible elements are
characterized by a rubber cord single-bellow (Fig. 1a-b) air spring filled with
gaseous medium. In the case of the load torque transmission, two
pneumatic-flexible elements are compressed and two are expanded simultaneously,
thereby ensuring the design of a two-sided pneumatic tuner. By means of the
valve (4), the compression space of
the pneumatic tuner is filled with gaseous medium in the range p=100÷700 kPa.
The design of the pneumatic tuner allows the individual pneumatic-flexible
elements to be interconnected by means of replaceable throttling nozzles (5) and hoses (6). To illustrate and present
the basic characteristics of pneumatic tuners of torsional oscillation, we only present the course of static characteristics in general. From the obtained results of static measurements, it has been shown
that, by changing the pressure of the gaseous medium, a pneumatic tuner is able
to work with different characteristic (Fig. 2); thus, it is capable of working
with other characteristic properties (torsional stiffness and damping
coefficient).
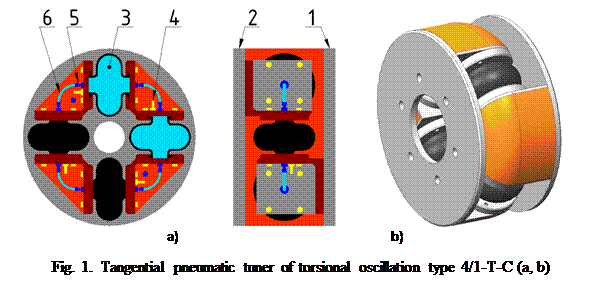
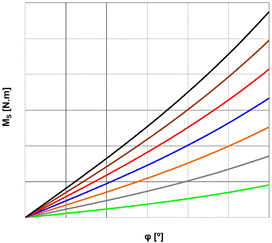
Fig. 2. Static
characteristics of pneumatic tuners of torsional oscillation in the pressure
range p=100÷700 kPa
Based on Fig. 2, it can
be stated that the characteristics of the pneumatic tuners are slightly
non-linear. We express them with the following equation:
(1)
3. TUNING Methods
FOR torsional oscillating mechanical systems
Changing the
torsional stiffness of pneumatic tuners can be accomplished by changing the
pressure of the gaseous medium, when out of operation or during the operation
of the mechanical systems. This results in two suggested methods of tuning:
Ø Tuning of torsional oscillating mechanical systems
that are out of operation, which fulfils the condition of the given mechanical
system tuning
Ø Tuning mechanical systems during an operation in a
steady state, thus ensuring the condition of the so-called continuous tuning of
the given systems.
By tuning the torsional oscillating
mechanical system with a pneumatic coupling, when out of operation, we mean to
inflate the compression space of the pneumatic tuner to the appropriate
pressure value of the gaseous medium before launching the system. At a given
pressure, the mechanical system will work throughout its operation. The
appropriate value of the pressure of the gaseous medium and thus the
appropriate value of the dynamic torsional stiffness of the coupling are
determined on the basis of the dynamic calculation of the system in terms of
torsional dynamics.
The suggested method of mechanical
systems tuning can be characterized as the “tuning of torsional oscillating
mechanical systems”, which is only suitable for systems working at constant
operating speeds.
When investigating the proper tuning
of any torsional oscillating mechanical system operating at constant operating
speeds, we start with the Campbell diagram (Fig. 6), which shows the positions
of critical speed nK
(or the position of the critical angular speeds ωK) depending on
the natural speed frequencies N (or
its natural angular frequencies W0).
4. CHARACTERISTICS
of the torsional oscillating mechanical system
The torsional oscillating mechanical
system (Fig. 3) consists of a driving part (1),
a pneumatic tuner of torsional oscillation (3)
and a driven part (2). The driving
part consists of a 16-kW direct current electric motor and an additional thyristor speed regulator (4) with the possibility of speed control in the range n=0÷2,000 min-1. A pneumatic
tuner is used to drive an exciter of torsional oscillation, represented by a
three-cylinder compressor mounted on the insulated layer (5). In order to increase the torsional impact introduced by the
compressor into the mechanical system, we use a compressor without a flywheel.
The load of the torsional oscillating mechanical system from the compressor
will be regulated by a throttle valve (6)
built into the outlet pipe of the compressor. This means that the load of the
system will be controlled and its load value will be characterized by the
pressure in the outlet pipe (pk), as read from the pressure gauge (7). In theoretical analysis and
experimental measurements, the pressure in the range pk=0.2÷0.8 MPa is
considered to correspond to the minimum or maximum load torque at certain
operating speeds of the system.
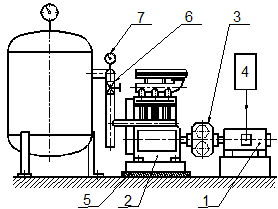
Fig. 3.
Torsional oscillating mechanical system
4.1. Analysis of the pneumatic tuner of torsional
oscillation load
The analysis of the load of the
pneumatic tuner of torsional oscillation when the mechanical system is in a
steady state will be investigated on the basis of a schematic model of the
torsional oscillating mechanical system (Fig.
4).
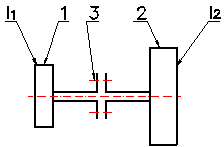
Fig. 4. Schematic model of a torsional
oscillating mechanical system
When calculating
the stress for the steady state of the mechanical system within its working
mode, let us assume that the mechanical system rotates at angular velocity
ω, which varies over a wide range. A load torque acts on the mass (1) with the moment of inertia I1 in the shape 
. It follows from this relation that
the pneumatic tuner, and hence the whole torsional oscillating mechanical
system, are loaded both by the medium torque MN, which does not change with the time in the steady
state, and by the action of the harmonic component Mi. As a result, a component of additional dynamic
torque Md
is introduced into the pneumatic tuner. Thus, the pneumatic tuner of torsional
oscillation will be loaded in this case by the load torque MS, which causes its maximum twist angle, φS.
(2)
(3)
The magnitude of the additional dynamic torque
and the dynamic element of the maximum twist angle calculated from the motion
equations (4) can be characterized by relations (5) and (6).
(4)
, (5)
, (6)
5. THEORETICAL RESULTS
OF optimal tuning OF a torsional oscillating mechanical system
Based on
the theoretical results characterizing the size of torsional vibration, we
evaluate the tuning of a torsional oscillating mechanical system. The size of
torsional oscillation of the torsional oscillating mechanical system will be
presented by:
Ø the amplitudes of torque oscillation in the pneumatic
coupling depending on speed
Ø the dynamics twist angle amplitude of the coupling
depending on speed
5.1. Results of the application of a
tangential pneumatic tuner of torsional oscillation
The Campbell diagram, according to Fig. 6,
characterizes the tuning of the mechanical system operating in the speed range n=750÷1,500
min-1 by the tangential pneumatic tuner of torsional
oscillation.
The diagram
shows the critical speed positions nk when dependent on the actual speeds N. The natural speeds are represented by
the horizontal lines a, b, c, d, e, f, g
for the entire gas pressure range of the pneumatic tuner p=100÷700 kPa. Based on the figure, it can be stated that the
pneumatic tuner is capable of operating under all pressures of gaseous medium (p=100÷700 kPa).
On the other hand, in terms of dynamic tuning, we are able to state that
pneumatic tuning will be suitable for the given system under pressures p=200÷600 kPa.
This is due to the resonance at the beginning of the operating mode at p=100 kPa with
the first harmonic component of the load torque at n=820 min-1, while, at p=700 kPa, the resonance also occurs with
the first harmonic component, but at n=1,480
min-1.
Based on the above, we will focus on the
dynamic tuning characteristic of the realized system in the pressure range p=200÷600 kPa.
Based
on the Campbell diagram (Fig. 5), it can be stated that the given tuner shifts
the second to 12th harmonic component from the operating range. Critical speeds
from the main harmonic component (i=3) at pressures p=200,
300, 400 and 600 kPa occurs at nk=330, 360, 405, 440
and 460 rpm. These values indicate that the torsional oscillating mechanical
system is very well tuned due to the start of the operating mode. This fact is
confirmed by the frequency ratio h=i.n/N, which, for the investigated
pressures, acquires relatively high values of h=2.3÷1.6.
At the same time, we can see that the first harmonic component is reached in
the range of gaseous pressure p=200÷600
kPa and in the operating speed range (n=750÷1,500 min-1). It
follows that, when using a pneumatic tuner, resonance with the harmonic
component occurs at the given pressures. In particular, for pressures p=200, 300, 400, 500 and 600 kPa, resonances occur at nk=980, 1,090, 1,220,
1,330 and 1,430 rpm.
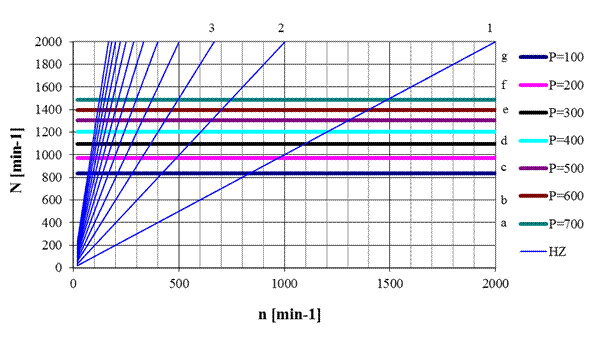
Fig. 5. Campbell diagram of a
mechanical system with an applied pneumatic tuner of torsional oscillation
(type 4-1/70-T-C) with constant pressures in the range p=100÷700 kPa
A suitable tuning of the torsional
oscillating mechanical system by the tangential pneumatic tuner of torsional
oscillation in relation to the main harmonic component (i=3),
as well as the operating speed range (n=750÷1,500 min-1), is
also confirmed by Figs. 6 and 7. Fig. 6 characterizes the dependency of the
load torque dynamic component Md on
speed n, while Fig. 7 characterizes the course of the dynamic twist
angle φd, depending on speed
of the mechanical system with an applied tangential pneumatic tuner of
torsional oscillation under constant pressures in the range p=100÷700 kPa.
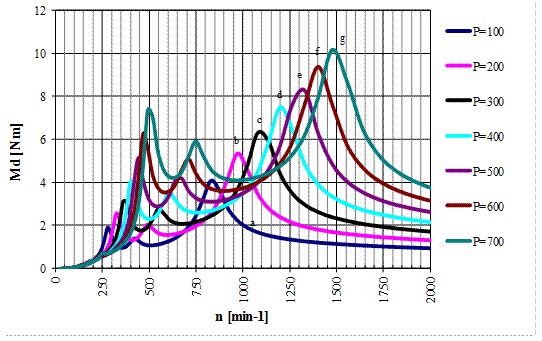
Fig. 6. Dynamic components of load
torque Md
in speed range n=0÷2,000 min-1
of a torsional oscillating mechanical system with the application of a
tangential pneumatic tuner of torsional oscillation (type 4-1/70-T-C) under
constant pressures in the range p=100÷700
kPa
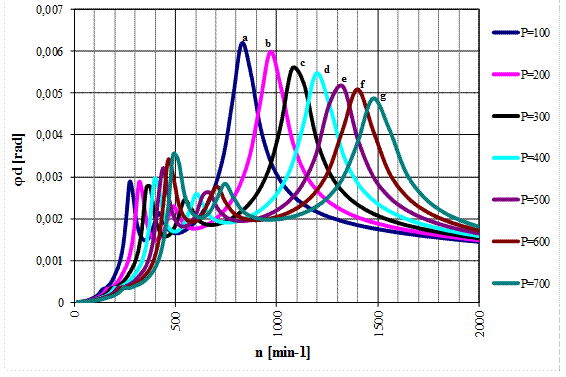
Fig. 7. Dynamic components of the
twist angle jd in
the speed range n=0÷2,000 min-1
of a torsional oscillating mechanical system with the application of a
tangential pneumatic tuner of torsional oscillation (type 4-1/70-T-C) under
constant pressures in the range p=100÷700
kPa
6. CONCLUSION
Based
on the presented results, it can be stated that the presented pneumatic tuners
of torsional oscillation fulfil all requirements in terms of their application
in torsional oscillating mechanical systems with both constant operating speeds
and a range of operating speeds. At the same time, it was confirmed that
reducing the adverse consequences of unforeseen disturbances that occur in
mechanical systems is possible by applying the proposed optimization of
torsional oscillating mechanical systems.
References
1.
Ankarali A., Z. Mecitoğlu, H. Diken. 2012.
“Response spectrum of a coupled flexible shaft-flexible beam system for
cycloidal input motion”. Mechanism and
Machine Theory 47: 89-102. ISSN: 0094114X.
2.
Bingzhao G., C.
Hong, Z. Haiyan, S. Kazushi. 2010. “A Reduced-order nonlinear clutch pressure
observer for automatic transmission”. IEEE
Transactions on Control Systems Technology 18(2): 446-453.
3.
Böhmer J. 1983. Einsatz elastischer vulkan-kupplungen mit linearer und progressive drehfeder-charakteristik.
[In German: Use of Elastic Volcano
Clutches with Linear and Progressive Torsion Spring Characteristic.]
Berlin: MTZ Berlin 44/5.
4.
ČSSR 259224 B6. Pneumatická pružná hriadeľová spojka s reguláciou tlmenia.
[In Slovak: Pneumatic Flexible Shaft
Coupling with Damping Control.] Vysoká škola technická v Košiciach, ČSSR. 25 June 1987.
5.
Czech
P., J. Mikulski. 2014. “Application of Bayes Classifier and Entropy of
Vibration Signals to Diagnose Damage of Head Gasket in Internal Combustion
Engine of a Car”. In: J. Mikulski (ed.). 14th International Conference on
Transport Systems Telematics. Katowice Ustron,
Poland. 22-25 October 2014. Telematics - Support for Transport. Book series:
Communications in Computer and Information Science, Vol. 471: 225-232.
6.
Czech P. 2013. “Intelligent
approach to valve clearance diagnostic in cars”. In: J. Mikulski (ed.). 13th
International Conference on Transport Systems Telematics.
Katowice Ustron, Poland. 23-26 October
2013. Activities of Transport Telematics.
Book series: Communications
in Computer and Information Science, Vol. 395:
384-391.
7.
Figlus Tomasz, Marcin Stańczyk.
2016. “A method for detecting damage to rolling bearings in toothed gears of
processing lines”. Metalurgija
55(1): 75-78. ISSN: 0543-5846.
8.
Figlus Tomasz, Marcin Stańczyk.
2014. “Diagnosis of the wear of gears in the gearbox using the wavelet packet
transform”. Metalurgija
53(4): 673-676. ISSN: 0543-5846.
9.
Folega Piotr, Grzegorz
Wojnar, Rafał Burdzik, Łukasz Konieczny. 2014. “Dynamic model of
a harmonic drive in a toothed gear transmission system”. Journal of Vibroengineering 16 (6):
3096-3104. ISSN 1392-8716.
10.
Gąska Damian, Tomasz Haniszewski,
Jerzy Margielewicz. 2017. “I-beam girders dimensioning with
numerical modelling of local stresses in wheel-supporting flanges”. Mechanika 23(3):
347-352. ISSN 1392-1207.
11.
James D., Van de Ven, J.
Cusack. 2014. “Synthesis and baseline testing of a digital pulse-width-modulated
clutch”. Mechanism and Machine Theory
78: 81-91. ISSN: 0094114X.
12.
Krejčíř O. 1986. Pneumatická vibroizolace.
[In Czech: Pneumatic Vibration Isolation.]
Liberec: DDP.
13.
Lacko P., V. Lacko 2000. “Continuously driven resonance”. Strojárstvo
42 (3/4): 127-135.
14.
Pešík L., P. Němeček. 1997. Identification
of the Dynamic System of a Machine with an Elastic Base. Chicago, USA: McNU 97.
15.
SR
5276 B1. Pneumatická spojka bez prepojenia pružných dutých telies v tvare kotúča. [In Slovak: Pneumatic
Coupling Without Linking Elastic Hollow Bodies in the Shape of a Disc.] Technická univerzita v Košiciach, SR. 12 August 2009.
16.
SR
5277 B1. Pneumatická spojka so zabudovaným škrtiacim prepojením pružných dutých telies. [In Slovak: Pneumatic
Coupling Without Linking Elastic Hollow Bodies in the Shape of a Disc.] Technická univerzita v Košiciach, SR. 12 August 2009.
17.
SR 278025. Pneumatická pružná hriadeľová spojka so schopnosťou autoregulácie. [In Slovak: Pneumatic Flexible Shaft Coupling with
Self-regulating Capability.] Technická univerzita v Košiciach, SR. 1995.
18.
SR
278272. Pneumatická spojka s prídavným regulátorom konštantného uhla skrútenia. [In Slovak: Pneumatic Coupling with Additional Constant
Curve Angle Regulator.] Technická univerzita v Košiciach, SR. 1996.
19.
SR 6219 B6. Pneumatická pružná hriadeľová spojka s prídavným regulátorom konštantného uhla skrútenia. [In Slovak: Pneumatic
flexible shaft coupling with additional constant-angle twist regulator.] Technická univerzita v Košiciach, SR. 3 September 2012.
20.
SR
5274 B1. Mechanická sústava optimálne vyladená pneumatickou spojkou. [In Slovak: The Mechanical System Is Optimally Tuned by the Pneumatic Coupling.]
Technická univerzita v Košiciach, SR. 25 June 2009.
21.
Wittek Adam Marek,
Damian Gąska, Bogusław Łazarz, Tomasz Matyja. 2014. “Automotive stabilizer bar – stabilizer
bar strength calculations using FEM, ovalization of
radial areas of tubular stabilizer bars”. Mechanika 20(6): 535-542. ISSN
1392-1207.
22.
Yubao S., W. Jihong, Y. Dianlong, W. Xisen. 2013. “Analysis and enhancement of torsional
vibration stopbands in a periodic shaft system”. Journal of Physics D: Applied Physics 46 145306: 7-13. ISSN
0022-3727.
23.
Zoul Václav
1984. Torzní vibrace v pohonech a způsob jejich snižování. [In Slovak:
Torsion Vibration in Drives and Their
Reduction.] Prague: ČSVTS.
VEGA 1/0473/17 “Research and development of
technology for homogeneous charge
self-ignition using compression in order to increase engine efficiency and to
reduce
vehicle emissions”
Received 04.08.2017; accepted in revised form 29.10.2017
Scientific Journal of Silesian
University of Technology. Series Transport is licensed under a Creative
Commons Attribution 4.0 International License