Article citation information:
Krasuski, K. Application of the GPS/EGNOS
solution for the precise positioning of an aircraft vehicle. Scientific Journal of Silesian University of
Technology. Series Transport. 2017, 96,
81-93. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2017.96.8.
Kamil KRASUSKI[1]
APPLICATION OF THE GPS/EGNOS
SOLUTION FOR THE PRECISE POSITIONING OF AN AIRCRAFT VEHICLE
Summary. The results of research
concerning the implementation of the GNSS technique in the area of air navigation
are presented in this article. In particular, a research test was conducted for
the purposes of checking the functioning of a satellite-based augmentation
system (SBAS) to assist with air navigation. Ultimately, analyses of the
parameters of accuracy, availability, continuity and integrity with the
procedure when landing aircraft with an SBAS APV-I landing were conducted. The
navigation and observation data of the GPS system and differential European
Geostationary Navigation Overlay Service (EGNOS) corrections were used in the
research test. The navigation and observation data of the GPS system in the
RINEX format were registered through the Topcon Hiper Pro receiver placed in
the cabin of pilots in the Cessna 172 aircraft during a flight experiment conducted
in Dęblin in 2010. The coordinates of the Cessna 172 aircraft in the ellipsoid
BLh frame were reconstructed by using the solution offered by the single point
positioning (SPP) method in the RTKLIB program. The accuracy when setting
coordinates of the aircraft is higher than 2.4 m in the horizontal plane and
better than 4 m in the vertical plane. The integrity of the satellite
positioning is higher than 15 m in the horizontal plane and better than 21.1 m
in the vertical plane. The availability of the constellation of GPS/EGNOS
satellites equalled 100% during the flight experiment, which confirms that the
loss of continuity when determining the position of the aircraft did not occur.
The parameters of the accuracy and the integrity with International Civil
Aviation Organization (ICAO) technical standards were compared in this article.
The results of the conducted test shows that the presented research methods can
be applied in the precise positioning of the aircraft when using the GPS/EGNOS
solution for air navigation.
Keywords: GPS; EGNOS; air transport; air
navigation; SPP method
1. INTRODUCTION
Within air navigation, an SBAS system assists with the
positioning of an aircraft when using the GNSS technique. The system is based
on the application of differential corrections from geostationary satellites in
order to improve the positioning of aircraft in almost real time, as well as
during post-processing [4]. In the main, WAAS, EGNOS, GAGAN, SDCM and MSAS
satellite systems support SBAS-based assistance [13]. There is an applied EGNOS
satellite system in Europe for the purposes of conducting precise air
navigation and air transport. The EGNOS system mainly improves accuracy when
determining the position of a user on the basis of a solution involving a GPS,
GLONASS or Galileo navigation system. The basic architecture of the EGNOS
system consists of the space segment, the ground section and the user’s
section. The space segment is created by the constellation of three EGNOS
satellites located in geostationary orbit, i.e., satellite numbers S120, S126
and S136. The ground segment consists of a network of reference stations
running the EGNOS, i.e., the RIMS, MCC, NLES stations. Next, in the user’s
section, it is possible to single out online services that support precise
positioning in the EGNOS system, that is, Open Service, Safety of Life and the EGNOS Data Access Service [6, 10, 18].
Tab.
1
Basic parameters of the SBAS APV-I landing procedure [2]
|
Air operation |
Parameter |
Value |
|
SBAS APV-I landing procedure |
Accuracy |
16 m for
horizontal plane, 20 m for
vertical plane |
|
Availability |
0.99 to
0.99999 |
|
|
Time to alarm |
10 s |
|
|
Continuity |
8*10-6
in any 15 s |
|
|
Integrity |
40 m for
horizontal plane, 50 m for
vertical plane |
In the case of
air navigation, the principles for using the EGNOS support system were set out
in the ICAO’s technical standards found in Annex 10 on radio navigation aids in
the Chicago Convention. In particular, the EGNOS system is applied as part of
an aircraft’s attempt to land according to the concept of area navigation
(RNAV). Therefore, the EGNOS support system can be used in the final approach
of the type SBAS APV-I [5]. The technical standards of the SBAS APV-I procedure
were developed for their implementation and exploitation of the Safety of Life
user service. In Table 1, basic technical parameters are presented for the SBAS
APV-I approach according to ICAO recommendations [9]. Within the framework of
the SBAS APV-I approach for the EGNOS system, the accuracy when determining the
position of aircraft cannot exceed 16 m in the horizontal plane and must be at
least 20 m in the vertical plane. The parameter of the integrity of satellite
positioning cannot exceed 40 m for horizontal navigation and 50 m for vertical
navigation. Moreover, the time to alarm must equal 10 s in cases in which
navigational data are lost from the EGNOS system. The
visibility of the constellation of EGNOS satellites and the GPS (if necessary,
GLONASS or Galileo) must be higher than 0.99 throughout the entire duration of
the air operation.
As part of the presented
work, the possibility of using differential EGNOS corrections for the precise
positioning of the aircraft was reported for the purposes of SBAS-based
assistance with air navigation. Verification of the use of the EGNOS system in
air navigation was carried out before the launch of a fully operational service
for Safety of Life activities (i.e., before 2 March 2011). The position of the
Cessna 172 aircraft was determined in a research experiment during the flight
test around the military airport in Dęblin on 1 June 2010. The position of the
aircraft was determined by the RTKPOST module in the RTKLIB software, based on
the SPP method. During calculations, corrective EGNOS data from the S126
satellite were used in the post-processing mode.
This article is divided
into three parts: Materials and Methods, Results and Discussion, and
Conclusions. The mathematical models for determining the position of the
aircraft using the SPP method are presented in the Materials and Methods part
of this article. In addition, the flight trajectory of the Cessna 172 aircraft,
the parameter of the Vertical TEC (VTEC) ionosphere, and the configurations of
parameters during calculations are also presented. The availability of the
constellation of GPS/EGNOS satellites and navigational continuity involved in
determining the position of the aircraft are presented in Results and
Discussion part of the article. In addition, the accuracy of the aircraft’s
coordinates are presented, the values of the MRSE parameter have been
determined, the values of the HPL and VPL safety levels are given presented,
and parameters of the accuracy and integrity of the ICAO technical standards
are compared in this section. In the Conclusions chapter, the outcomes are summarized.
2. METHODS AND MATERIALS
The data for
EGNOS correction are used in the SPP method for the determination of
coordinates of the aircraft during the performed flight. Mathematical models
for determining the position of the aircraft from the EGNOS solution are
described below:
(1)
where:
– pseudorange value
(C/A code) for the initial frequency in GNSS system (e.g., in the GPS system)
– geometric distance
between the satellite and receiver
– the aircraft’s
coordinates in the geocentric frame
– GNSS satellite
coordinates (e.g., GPS system)
– speed of light
– receiver clock bias
– satellite clock bias
– ionosphere delay
– troposphere delay
– relativistic effect
– time group delay
– receiver differential code bias, referenced to the L1-C/A
code
– differential correction from the EGNOS system including
long-term and fast corrections, and ionosphere and troposphere corrections
- measurement noise
Geocentric coordinates of the
aircraft are determined by using the least-squares method in the process-based
iteration for all measurement epochs as per below [8]:
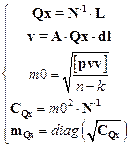(2)
where:
– vector with unknown parameters
– matrix of normal equation frame
– full rank matrix
– matrix of weights
– misclosure vector
– vector including the difference between observations and
modelled parameters
– standard error of unit weight
– number of observations, 
for each measurement
epoch
– number of unknown parameters, 
for each measurement
epoch
– vector of residuals
– covariance matrix
– standard deviations for unknown parameters
Set coordinates of the aircraft can also be expressed with ellipsoid BLh
coordinates, as per below [14]:
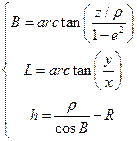(3)
where:
– semi-major and semi-minor axes of the ellipsoid frame
– eccentricity
– radius of the curvature of the prime vertical
– geodetic coordinates of the aircraft’s position
– latitude
– longitude
– ellipsoidal height
The accuracy of
coordinates of the aircraft related to the geodetic BLh frame is described with
parameters [12] below:
(4)
where:
– covariance matrix in geodetic frame (BLh)
– transition matrix from geocentric (XYZ) to geodetic frame
(BLh)
– standard deviation in latitude
– standard deviation in longitude
– standard deviation in ellipsoidal height
Within the framework of the conducted research, the position of the
Cessna 172 aircraft was determined using EGNOS correction data. A test flight
was carried out in the area of the military airport in Dęblin on 1 June 2010
between the hours of 09:39:03 and 10:35:03 according to the time indicated by
the GPS. The mobile geodetic Topcon Hiper Pro receiver, which was placed on
board the aircraft, was designed to facilitate GNSS observation for the
purposes of reconstructing the real position of the Cessna 172 aircraft in the
post-processing mode [1]. The Topcon Hiper Pro receiver recorded satellite
observations from the GPS and the GLONASS system with a frequency of every 1 s.
Moreover, for the purposes of research tests, EGNOS correction data from the
S126 satellite were used and placed on the Internet server: http://www.egnos-pro.esa.int/ems/index.html.
The frequency by which differences in EGNOS corrections were recorded was also
every 1 s. The final trajectory of the Cessna 172 aircraft in the coordinate
frame of the ellipsoidal BLh is shown in Fig. 1.
As part of the
conducted air test, the state of the ionosphere in the form of the VTEC
parameter was also determined. Values of the ionosphere VTEC delay were
determined in the EGNOS system by using a regular GRID with a size of about 5°
on 5°. Fig. 2 presents the values of the VTEC parameter for the knot of the
GRID, whose coordinates are 50° N 20° E, which are based on differential EGNOS
corrections from the S126 satellite. During the flight experiment, the value of
the ionosphere VTEC delay changed from 1.375 to 1.625 m. The average value of
the VTEC parameter was equal to 1.530 m, while the median was equal to 1.500 m.
The values of the ionosphere VTEC delay was calculated using SBAS MeNTOR 1.15
software [3].
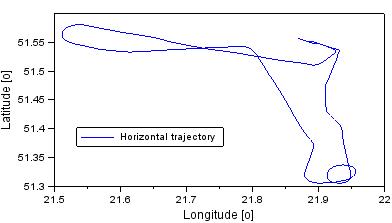
Fig. 1. Horizontal flight trajectory
of the Cessna 172 aircraft
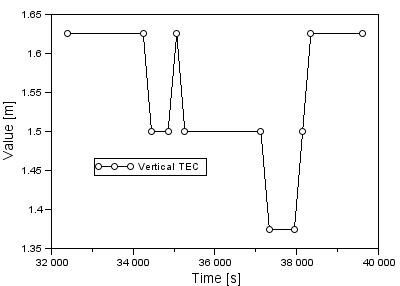
Fig. 2. Values
of the VTEC parameter during the flight test
Calculations of
ellipsoid coordinates of the aircraft were performed by using the SPP method in
the RTKPOST module of the RTKLIB program. The GPS code observations in the
RINEX 2.11 format, the GPS navigational data and differential EGNOS corrections
in the EMS format were also used in the calculations. The configuration of the
RTKPOST module was adjusted for the purposes of calculations, as below [16]:
- positioning mode: single
- elevation mask: 5°
- source of ionosphere delay: SBAS
correction
- source of troposphere delay: SBAS
correction
- source of satellite coordinates
and clocks: broadcast ephemeris and SBAS message
- GNSS system: GPS + SBAS
- source of GPS observations: RINEX
2.11 file
- source of EGNOS corrections: EMS
file
- reference frame of coordinates:
WGS-84 datum
3. RESULTS AND DISCUSSION
Fig. 3 presents
the number of visible GPS and EGNOS satellites during the flight experiment at
the airport in Dęblin. The required number of satellites to determine the
navigation position of the aircraft in a single measurement epoch is typically
four or more. The parameter of the availability of the GPS and EGNOS
constellation of satellites on 1 June 2010 amounted to 100% and the number of
satellites changed from six to 10. It should be noted that, in the first stage
of the flight (i.e., the start and the departure from the airport), the number
of GPS and EGNOS satellites tracked by the receiver was between six and 10. In
the final stage of the flight (i.e., approach to landing) the number of GPS and
EGNOS satellites evolved from six to nine. The average number of visible GPS
and EGNOS satellites during the experiment was more than nine. A sufficient
number of visible GPS and EGNOS satellites also enabled continuity solutions
for determining the positions of the aircraft with the SPP method. To this
extent, there were no breaks or losses regarding the solution for determining
the Cessna 172 aircraft’s position.
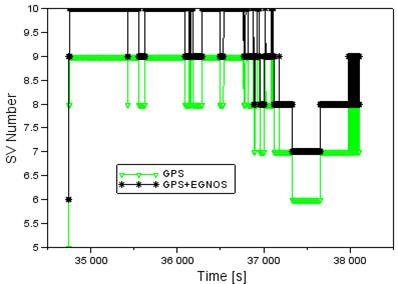
Fig. 3. The
GPS/EGNOS satellite constellation during the flight test
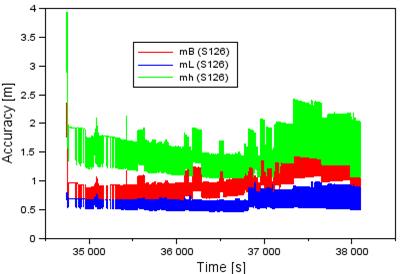
Fig. 4. The
accuracy of the geodetic coordinates of the Cessna 172 aircraft
Fig. 4 presents
the accuracy when setting the geodetic coordinates for the Cessna 172 aircraft
during the conducted flight test. The standard deviation of the geodetic
latitude width changed from 0.6 m to 2.4 m, while the average value of the
accuracy of the B horizontal coordinates was equal to around 1 m. The standard
deviation of the geodetic longitude changed from 0.5 m to 1 m, while the
average value of the accuracy of the L horizontal coordinates was equal to
around 0.7 m. The standard deviation of the ellipsoidal height h changed
by 1 m to almost 4 m, while the average value of the accuracy of the vertical
coordinate h was equal to around 1.6 m. The parameter of the median
accuracy for the individual coordinate was equal to around 1 m for the B
coordinate, 0.7 m for the L coordinate and 1.5 m for the ellipsoidal height.
Moreover, it is noteworthy that the accuracy when appointing the geodetic
longitude was higher than the accuracy of the geodetic latitude and
ellipsoidal height.
Tab.
2
The
comparison of accuracy parameters during the SBAS APV-I procedure
|
Parameter |
Obtained accuracy for each BLh
geodetic coordinates |
Accuracy of SBAS APV-I
procedure according to ICAO convention |
Conclusions |
|
Value |
Dispersion of
standard deviation in latitude was between 0.6 m and 2.4 m |
16 m for
horizontal plane |
The obtained
accuracy for latitude did not exceed the ICAO standard in the horizontal
plane |
|
Dispersion of
standard deviation in longitude was between 0.5 m and 1 m |
16 m for
horizontal plane |
The obtained
accuracy for longitude did not exceed the ICAO standard in the horizontal
plane |
|
|
Dispersion of
standard deviation in ellipsoidal height was between 1 m and 4 m |
20 m for
vertical plane |
The obtained
accuracy for the ellipsoidal height did not exceed the ICAO standard in the
vertical plane |
A comparison of
the results of the geodetic BLh coordinates for the Cessna 172 aircraft and the
ICAO’s technical standards is presented in Table 2. The ICAO’s technical
standards were published in Annex 10 on radio navigation aids in the Chicago
Convention [7]. Based on the obtained test results, it is possible to state
that the values of the standard deviation in the coordinates of the Cessna 172
aircraft did not exceed the theoretical accuracies in the SBAS APV-I procedure.
Regarding navigation in the horizontal plane, the latitude and longitude
accuracy was definitely higher than 16 m. In the vertical plane, the obtained
accuracy of the ellipsoidal height did not exceed 20 m. It is also
necessary to emphasize that the obtained value of the standard deviation in the
aircraft coordinates in the BLh ellipsoidal system can be utilized to the
determine the parameter concerning the integrity of satellite positioning.
The values of
the mean radial spherical error (MRSE) parameter for the conducted flight test
are presented in Fig. 5. The values of the MRSE parameter were determined as
follows [15]:
(5)
The
obtained value of the MRSE parameter was between 1.3 m and 4.7 m. Moreover, the
average value of the MRSE parameter was equal to 2 m, while the median was
equal to 1.9 m. The MRSE parameter is of special importance for locating
aircraft in three-dimensional space.
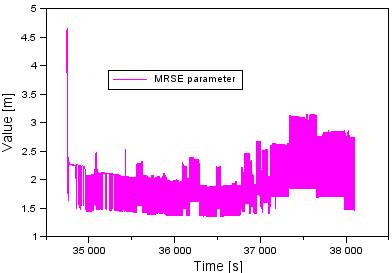
Fig. 5. The
MRSE parameter values of during the flight test
Fig. 6 presents
the safety level values of the flight operation in the form of the horizontal
protection level (HPL) and the vertical protection level (VPL) parameters.
Parameters concerning the integrity of satellite HPL and VPL positioning were
determined by the following mathematical formula [11]:
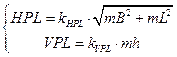(6)
where:
(horizontal plane)
(vertical plane)
The HPL and
VPL safety levels parameters, which describe the integrity of the satellite positioning
for the SBAS APV-I approach, are determined on the basis of the values of the
accuracy of geodetic BLh coordinates. The
HPL parameter assumed values between 4.7 m and 15 m. Moreover, the average
value of the HPL parameter was equal to 7.3 m, while the median was
appropriately 7 m. The obtained value of the VPL parameter was 5.6 m and 21.1
m, respectively. In addition, the average value of the VPL parameter was equal
to 8.3 m, while the median was equal to 7.8 m. It is worth pointing out that HPL
and VPL parameter values showed an increasing trend during the procedure of the
final approach.
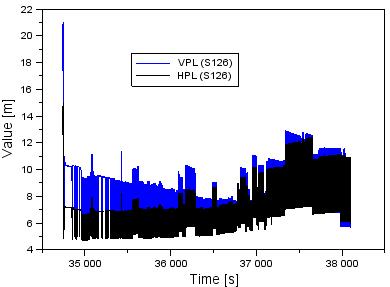
Fig. 6. The values of
the HPL and VPL parameters
A comparison of
the results related to the HPL and VPL integrity parameters and the ICAO’s
technical standards is presented in Table 3. The ICAO’s technical standards
were included in Annex 10 on radio navigation aids in the Chicago Convention [7].
Based on the obtained test results, it is possible to state that the HPL and
VPL values did not exceed the border alerts in the SBAS APV-I procedure.
As for the horizontal plane, the HPL parameter values were definitely smaller
than the border level of the alarm, e.g., 40 m. On the vertical plane, the
obtained results for the VPL parameter did not transgress the safety level of
the flight operation for 50 m. It is also necessary to emphasize that the
obtained HPL and VPL parameter values improve the integrity of the navigational
solution for determining the aircraft’s position during the legal procedure for
the SBAS APV-I landing approach.
Tab. 3
Comparison of the integrity parameters during the SBAS APV-I procedure
|
Parameter |
Obtained integrity for each of
the BLh geodetic coordinates |
Integrity of the SBAS APV-I
procedure according to the ICAO convention |
Conclusions |
|
Value |
Dispersion of
the integrity term was between 4.7 m and 15 m |
40 m for the
horizontal plane |
The obtained
integrity parameter did not exceed the ICAO standard in the horizontal plane |
|
Dispersion of
the integrity term was between 5.6 m and 21.1 m |
50 m for the
vertical plane |
The obtained
integrity parameter did not exceed the ICAO standard in the vertical plane |
It is
noteworthy that the continuity in determining the HPL and VPL parameters was
maintained, while, in the course of calculations, no anomaly was detected in
terms of exceeding border alerts. The parameters for the continuity of the
integrity of the aircraft’s position are described below [17]:
(7)
where:
(maximum value of the alert in the horizontal plane)
(maximum value of the alert in the vertical plane)
The continuity
parameter was lost when the value of the HPL exceeded 40 m and the VPL was
greater than 50 m. Based on the presented results regarding the HPL and VPL
parameters, the continuity of the integrity of the satellite positioning during
the flight navigation was not lost.
4. CONCLUSIONS
In this article, the possibility of using the GNSS technique during an
aircraft’s SBAS APV-I landing procedure was presented. In the process, analyses
of the parameters of accuracy, integrity, availability and continuity regarding
this procedure were conducted. For the purposes of conducting the research experiment,
observations and GPS navigation data and differential EGNOS corrections were
used. Navigation and GPS observation data were stored in the memory of the
Topcon Hiper Pro receiver during an ongoing flight test using a Cessna 172
aircraft at the airport in Dęblin on 1 June 2010. The differential EGNOS
corrections from the S126 satellite were downloaded from the following web
server: http://www.egnos-pro.esa.int/ems/index.html. The input data were used
to recover the position of the Cessna 172 aircraft in the ellipsoidal BLh
frame. RTKLIB software was used for the calculation, while the SPP research
method was applied in order to set the aircraft’s coordinates. This article
also presented the trajectory of the aircraft in the ellipsoidal BLh, defined
the ionosphere VTEC parameter, identified the availability constellation of the
GPS/EGNOS satellites, and determined the navigational
continuity needed to establish the aircraft’s position. Furthermore, the
accuracy in establishing the aircraft’s position was determined, an MRSE
parameter identified, and parameters of the HPL and VPL safety levels
confirmed. Values of the accuracy and integrity parameters were compared with
the technical standards published in Annex 10 of the Chicago Convention.
According to the conducted examinations, it is possible to conclude that the
calculation results met the technical parameter criteria for the SBAS APV-I
approach. The availability of the constellation of GPS/EGNOS satellites
equalled 100%, thereby ensuring continuity in determining the position of the
aircraft. The parameters of the standard deviation in the coordinates of the
aircraft did not exceed the accuracy of the limits for the procedure of the
SBAS APV-I approach. Moreover, the HPL and VPL safety levels were below the
border alert levels for the SBAS APV-I procedure. Future work is planned in
order to check and verify the technical standards of the SBAS APV-I procedure
for the aerodromes in the cities of Mielec and Chełm.
Acknowledgements
The author would like to thanks
Henryk Jafernik PhD (PAFA, Dęblin) for making available the RINEX files from
the flight experiment conducted in Dęblin during 2010.
References
1.
Ćwiklak Janusz, Henryk Jafernik. 2010. “The monitoring system for aircraft and vehicles of public order services
based on GNSS.” Annual of
Navigation 16: 15-24.
2.
European GNSS Agency. 2015. EGNOS
Safety of Life (SoL) Service Definition Document, Issue 3.0. ISBN
978-92-9206-025-1. DOI:10.2878/851094.
3.
European Space Agency. 2010. User
Manual SBAS Mentor 1.15.
4.
Fellner Andrzej,
Janusz Ćwiklak, Henryk Jafernik, Paweł Trómiński, Józef Zając, Krzysztof
Banaszek. 2008. “GNSS for an aviation analysis based on EUPOS and
GNSS/EGNOS collocated stations in PWSZ CHELM.” TransNav 2(4): 351-356.
5.
Fellner Andrzej, Henryk Jafernik. 2014. “Airborne measurement system during validation of EGNOS/GNSS essentials
parameters in landing.” Reports of
Geodesy and Geoinformatics 96: 27-37. DOI: 10.2478/rgg-2014-0004.
6.
Fellner Radosław. 2014. “Analysis of the EGNOS/GNSS parameters in
selected aspects of Polish transport.” Transport Problems 4(4): 27-37.
7.
Grunwald Grzegorz,
Adam Ciećko, Mieczysław Bakuła, Rafał Kaźmierczak. 2016. “Examination of GPS/EGNOS integrity in north-eastern Poland.” IET
Radar, Sonar & Navigation 10(1): 114-121. DOI: 10.1049/iet-rsn.2015.0053.
8.
Hofmann-Wellenhof Bernhard, Herbert
Lichtenegger, Elmar Wasle. 2008. GNSS –
Global Navigation Satellite
Systems: GPS, GLONASS, Galileo, and More. ISBN 978-3-211-73012-6. Vienna and New York: Springer.
9.
International
Civil Aviation Organization. 2006. ICAO Standards and Recommended Practices
(SARPS), Annex 10, Volume I (Radio Navigation Aids). Available at: http://www.ulc.gov.pl/pl/prawo/prawomi%C4%99dzynarodowe/206-konwencje.
10.
Jimenez-Baňos David,
Matthew Powe, Ankit Raj Matur, Felix Toran, Didier Flament, Eric Chatre. 2011. “EGNOS Open Service guidelines for receiver
manufacturers.” In: Proceedings of the 24th
International Technical Meeting of the Satellite Division of the Institute of
Navigation (ION GNSS 2011):
2505-2512.
11.
Jokinen Altti,
Shaojun Feng, Carl Milner, Wolfgang Schuster, Washington Ochieng, Chris Hide,
Terry Moore, Chris Hill. 2011. “Precise point
positioning and integrity monitoring with GPS and GLONASS.” Paper presented at the European Navigation
Conference 2011 in London, UK.
12.
Osada Edward.
2001. Geodesy. Wrocław: Oficyna
Wydawnicza Politechniki Wrocławskiej. ISBN 83-7085-663-2.
13.
Ostolaza Javier,
Ignacio Alcantarilla, Jose Caro, Juan Ramon Martin. 2011. “An efficient approach for the development
and deployment of a multi-constellation augmentation system: magicSBAS.” In: Proceedings of the 24th International
Technical Meeting of the Satellite Division of the Institute of Navigation (ION
GNSS 2011): 1486-1493.
14.
Sanz Subirana
Jaume, Jose Miguel Juan Zornoza, Manuel Hernández-Pajares. 2013. GNSS Data Processing. Volume
I: Fundamentals and Algorithms. Noordwijk, Netherlands: ESA Communications, ESTEC. ISBN 978-92-9221-886-7.
15.
Seeber Gűnter.
2003. Satellite Geodesy. Second
Completely Revised and Extended Edition. Berlin: Walter de Gruyter GmbH
& Co. KG, 10785. ISBN 3-11-017549-5.
16.
Takasu Tomoji. 2013. RTKLIB Ver. 2.4.2 Manual, RTKLIB: An Open Source
Program Package for GNSS Positioning: 29-49. Available at: http://www.rtklib.com/prog/manual_2.4.2.pdf.
17.
Vassilev Boris, Boriana Vassileva. 2012. “EGNOS performance before and after applying an error extraction
methodology.” Annual of Navigation
19(2): 121-130. DOI: 10.2478/v10367-012-0022-8.
18.
EGNOS. Available at:
https://egnos-portal.gsa.europa.eu/discover-egnos/programme-information/status.
Received 17.05.2017; accepted in revised form 04.08.2017
Scientific Journal of
Silesian University of Technology. Series Transport is licensed under a Creative
Commons Attribution 4.0 International License