Article citation information:
Jacyna, M., Gołębiowski, P., Krześniak, M. Some
aspects of heuristic algorithms and their application in decision support tools
for freight railway traffic organization. Scientific
Journal of Silesian University of Technology. Series Transport. 2017, 96,
59-69. ISSN: 0209-3324.
DOI: https://doi.org/10.20858/sjsutst.2017.96.6.
Marianna
JACYNA[1], Piotr GOŁĘBIOWSKI[2], Mirosław KRZEŚNIAK[3]
SOME
ASPECTS OF HEURISTIC ALGORITHMS AND THEIR APPLICATION IN DECISION SUPPORT TOOLS
FOR FREIGHT RAILWAY TRAFFIC ORGANIZATION
Summary.
Rail traffic organization is a multifactorial decision-making problem. To
achieve the best results and reduce the risk of error when deciding on its
implementation, appropriate algorithms should be identified and implemented in
the form of computer tools, allowing for the optimal solution to be obtained. This
paper discusses the process of organizing freight traffic on the rail network.
The algorithm of relocating loaded cars in a compact and dispersed system is discussed.
In turn, it is been indicated that the movement of empty and loaded cars must
follow a strictly defined timetable. A heuristic algorithm supporting
decision-making in the area of rail freight traffic management is presented,
divided between the concept development stage, the timetable design stage for
the developed concept, and its implementation in the form of specialized tools.
An example of how the application works is also presented.
Keywords:
rail transport; railway organization; relocation of cars; timetable design
1. INTRODUCTION
The
movement of trains on the rail network, due to the need to maintain the highest
degree of safety, must be appropriately ordered. This involves developing
proper traffic organization for a given situation. This is not an easy task in
light of the many factors affecting train traffic on the rail network. Among
the most important for freight traffic, four groups of factors should be
mentioned [18]:
- technical (e.g., ensuring the
continuity and safety of transport, adjusting the number and size of trains to
the size of freight flow, regulating the capacity of railway lines and
stations)
- technological (e.g., minimizing
transit time, regulating train service standards at railway stations,
developing proper organization of train station operations)
- organizational (e.g., comprehensive
fulfilment of transport demand, conducting train traffic according to
documentation, ensuring transport efficiency, rational circulation and composition
of trains, rational timetable construction, obtaining appropriate values of
indicators, cooperation with external parties to ensure delivery on time)
- random (e.g., variable demand for
transport, rolling stock and infrastructure failures)
At
present, the customer plays a major role in the transport market. Operators
(carriers) have to adapt to their needs. Transport services must therefore be
provided at an appropriate level; otherwise, the potential sender may decide to
choose another service provider. Rail carriers, on the one hand, must meet
their customers’ expectations in a timely, fast, reliable, efficient,
economical and secure manner [15]; on the other hand, market
expectations are clearly defined. Customer needs are important in terms of both
passenger and freight traffic.
To
adapt to the railway market, the infrastructure manager must strive to meet all
needs: for operators and for customers. The proper preparation of a train
timetable plays a major role in this process, due to the specificity of rail
traffic, that is, to place the train path in time and space in a safe manner,
respecting the needs of the customers. The problem with timetable construction
involves the determination of train paths based on the traffic graph [1, 4, 8, 9, 17, 21]. In the process of assigning
routes for trains, the priorities on the traffic graph should be taken into
account [20], as well as multiple technical and
operational factors, including railway traffic regulations [19].
The
construction of a rational train timetable is not the only problem associated
with the organization of rail traffic. In the case of freight traffic [3, 16], the issue of providing empty cars
for loading at the dispatch station at a time specified by the sender is also
important. The problem is therefore to designate stations with the appropriate
number of cars of a specific type, which will allow for the needs of customers
to be satisfied and transporting the cars to the dispatch station according to
the pre-arranged timetable. Thus, it is a complex problem that occurs in all
transport areas [12, 13, 24, 22, 27]. According to the literature, the
subjects of research are, among others, the efficiency of supplies [11], their reliability [10] or efficiency [28]. Due to the complexity of these
problems, decision-making tools play an important role in modern railway
traffic organization.
The
development of computer techniques allows us to solve complex process models.
The use of IT in decision support processes is called a decision support system
[23]. Depending on the complexity of
the problem, user preferences and other factors, a correct system should be
chosen, which is often a dedicated system created to solve this specific
problem. A very important element in such a system is the algorithms used for
solving the decision problem, which must be properly implemented. Due to the
complexity of the problems to be resolved, genetic algorithms [14], neural networks [6] and other tools are employed.
To get
the best results and reduce the risk of error when deciding on the proper
deployment of rail traffic on the network, appropriate algorithms for the
solution must be identified [5], as well as their implementation
in the form of computer tools, which will help in the decision-making process.
The paper discusses in detail the procedure for organizing freight traffic on
the rail network. The algorithm for moving cars from the dispatch station to
the destination station in both compact and dispersed systems is also
discussed. It has been indicated that the movement of both empty and loaded
cars must be carried out according to a strictly defined timetable. A heuristic
algorithm supporting decision-making in the area of rail freight
traffic management is presented, divided between the concept development stage,
timetable design stage for the developed concept, and its implementation in the
form of specialized tools. An example of how the application works is also
presented.
2. PROCEDURE OF FREIGHT TRAFFIC
ORGANIZATION ON THE RAILWAY NETWORK
2.1. Introduction
The
organization of rail traffic consists of [8]:
- planning communication routes
(construction of transport offer)
- actual construction of the train
timetable (building train traffic charts)
- allocation of platform edges or
tracks at train stations
- rolling stock planning
- planning the work of teams serving
vehicles (conductor and traction teams)
- regulating train operating standards
at railway stations
- development of proper work
organization of railway stations
- regulating the capacity of lines and
railway stations
As
mentioned in the introduction, this is not a simple problem to consider. The
specificity of freight traffic organization is all the more complex, as the
movement of freight trains must be adapted to passenger traffic, which has a
higher priority [20]. In addition, shipments can be
performed in two systems: compact and dispersed.
A
compact system assumes that the transport of goods is performed using a fixed
wagon set from the dispatch station to the destination station. With
appropriate infrastructure in the transport nodes at both ends of the transport
route (sufficient length of siding tracks, appropriate siding capacity etc.),
this freight starts at the sender’s point of departure and ends at the
receiving point of the recipient.
Dispersed
transport is much more expensive than compact transport and requires a
disproportionate amount of manoeuvring and expedition work. The dispersed
transport system is based on the so-called node points system or a linear train
system.
The node points system assumes the
movement of individual wagon groups in accordance with accepted rules. Freight
trains for dispersed transport are compiled from properly selected wagon
consignments. The linear train system assumes that trains are run on a given
route to collect small shipments, which are not suitable for compact transport
due to the insufficient flow of cargo.
Technically, the dispersed movement
is a very complicated process. Compared to compact transport, it involves more
resources, including the need for more manoeuvring work. This method generates
much higher costs than the compact system. Particular attention should be paid
to the system used, as both the time and cost of moving wagons depend on the
technology of moving loaded and empty cars.
Therefore, the problem of organizing
freight traffic in rail transport is to provide a sufficient number of empty
cars for loading at the time indicated by the customer, as well as transporting
the cargo from the sender to the recipient according to the appropriate
transport technology (compact or dispersed). Both the delivery of cars and the
transportation from the sender to the recipient must follow a strictly defined
timetable.
2.2. Algorithm for car relocation on the railway network
The algorithm for car relocation on
the railway network is presented in fig. 1.
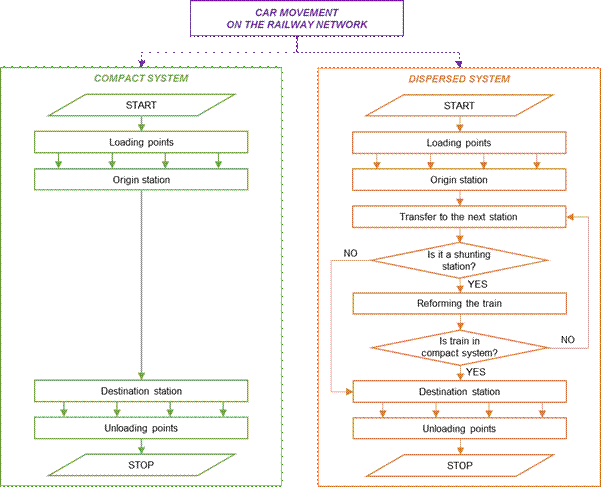
Fig. 1. The algorithm for car relocation on the railway network
As mentioned in Section 2.1, cars on
the railway network can be moved using two technologies: a compact system, when
the entire train is dispatched directly from the sender to the recipient; or
the dispersed system, when the cars with cargo from the particular sender to
the particular recipient are moved using different trains.
In a compact system, the cars
located at station and line loading points of individual senders are moved to
the dispatch station, where the train is formed. This entire train is then
directed to the destination station, from where the cars are sent to station
and line unloading points, i.e., to the final recipients. To run a compact
train, it should be determined whether or not it is economically justified.
If the number of cars at the
dispatch station does not allow a compact train to be run, the dispersed system
is then used. After delivery from station and line loading points to the
dispatch station, the cars are coupled with a train and routed to the nearest
shunting station. This station collects consignments from several dispatch
stations. After reforming them into one train, it is checked whether the newly
created train, containing cars from various stations of origin to the same
destination station, can be considered economically viable to be run in a
compact system. If so, the train is routed to the destination station, from
where the cars are distributed to station and line loading points in the
destination area. If not, the train is routed to the next shunting station to
repeat this step with more cars.
2.3. Assessment of traffic organization on the
railway network
Moving
cars in a compact or dispersed system, as well as the delivery of empty cars
for loading, must be carried out according to a prepared timetable. It is
created, based on a traffic graph, which is a graphical representation of train
routes in a distance/time layout. The first stage of building a timetable is to
determine the traffic graphs, which become the basis for the timetable. In
order to prepare a traffic graph, it is necessary to specify the following set
of input data:
- Set of control points and forwarding
offices on the proposed train route (node elements of railway transport
infrastructure)
- Set of sections on the proposed
train route (linear elements of railway infrastructure)
- Structure of the traffic graph
(possible time points and train states)
- Set of train types, which can be run
on a given route
- Values of parameters determining the
average stop time in a node
- Set of train numbers (identifiers)
to be run
- Leading hours for each of the trains
- Duration time of each train’s state
- Values of parameters determining the
length of station distances
- Values of parameters determining the
length of line distances
With
the above-mentioned set of input data, it is possible to begin modelling the
routing of trains on a traffic graph, based on the suggested leading hours. The
problem is therefore to find the trains’ paths x(t,po(t)) on the traffic
graph. Each of the paths consists of train states (halt and move). Next, the
prepared transportation offer should be checked for collisions with other train
routes, with all identified collisions removed. To assess the quality of the
resulting traffic graph, an indicator for operating costs ko(t) of running all the
trains has been used:
![]() (1)
(1)
where:
t ∈ T – a set of train
connections, in which the starting node and the end node are the forwarding
office where it is possible to respectively start and stop trains
A
minimum value of this indicator is desired. The model should take into account
the restrictions imposed on each train, which must be handled by only one train
set, with the assigned number of sets not exceeding the total number of
available sets. It is also important to establish the train numbers to be run: poc(t)
∈ POC(t) on particular routes t and the final leading hours for them,
i.e., gw(poc(t)) (the final
leading hour cannot be later than assumed in the case of empty cars’ delivery
and earlier in the case of starting a loaded train). Taking into account the
technical limitations, it is important to ensure that each vertex in the
traffic graph has only one successor and only one predecessor (excluding the
start and end vertices, which have no predecessor and successor, respectively).
3. HEURISTIC
ALGORITHM OF FREIGHT TRAFFIC ORGANIZATION ON THE NETWORK
As
already mentioned above, the organization of freight traffic on the railway
network is a complex decision-making process, on which customer satisfaction
strongly depends. Taking into account the existing conditions, two stages can
be distinguished in this process (see
fig. 2):
- STAGE 1, which is performed by the
railway carrier, consists of developing the plan for relocating empty cars to
loading points and loaded cars to the recipients (using compact or dispersed
system), as well as actual execution of the said plan.
- STAGE 2, which is performed by the
infrastructure manager, consists of developing the timetable for moving empty
and loaded cars on the network.
The
customer who places the order with the railway carrier initiates the procedure
of transporting the cargo from the sender to the receiver. In this order, the
customer specifies the moment of delivering the cars to the loading point and
the moment of completing the loading process (leading hours). Once the order is
placed, the carrier checks if it is possible to be completed. Firstly, the
necessary rolling stock to execute the order is identified and its location is
established. If empty cars are on the dispatch station, they are delivered to
the loading point, upon which loading begins. Otherwise, it should be verified
whether the necessary cars are available in the area of
the station (the boundaries of the area are determined by the railway company).
If so, all the stations with available cars are listed, together with the
cost of acquiring the rolling stock from each of the stations. The cost
minimization criterion is applied and the station, which is to be the source of
cars, is selected. If there are no suitable cars in the area, the search
continues throughout the entire railway network. For all these stations, the
cost minimization criterion is also applied, resulting in selecting the station
to be the source of cars for a given order.
Empty
cars, which are located outside of the dispatch station, are delivered for
loading to this station. It is only possible after preparing the timetable for
them to be safely relocated. This is done by the infrastructure manager, based
on a request for route assignment made by the railway carrier. As part of the
process, the timetable creators place specific train paths on the graphic
timetable. The first step is to analyse and validate the application to assign
a path for a train, submitted by the carrier (
fig. 2). In the case of errors, the
infrastructure manager returns the application to the carrier to be corrected.
Otherwise, the application is accepted for inclusion in the timetable
construction process.
Then
the construction process starts. The constructor, based on the parameters
declared in the application by the railway carrier, determines the values of
all the elements necessary to develop a traffic graph. The process begins with
collecting all the data necessary to properly build the traffic graph and
loading the data into the software. Next, the traffic graphs, on which the
train’s path will be drawn, are chosen (if the train runs through multiple
railway lines, it may be required to place it on multiple graphs).
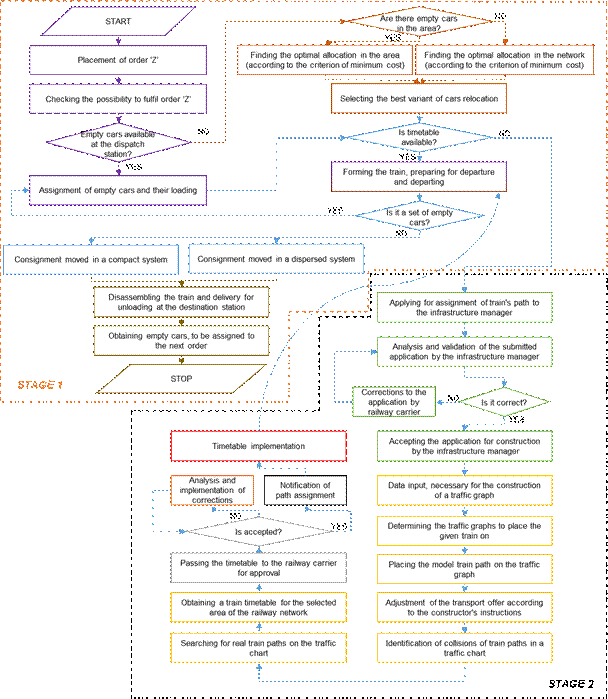
Fig. 2. Heuristic algorithm of freight traffic organization on
the railway network
After that, the
model path is applied to the traffic graph. Such a path may not meet all the
restrictions, while some collisions between trains may appear and the appropriate
safety level of railway traffic may not be met. This routing is based on the
declared leading hour, with the process conducted using the A* algorithm for
finding the shortest path in a graph [25]. Each arc is described by the time
required to travel by it. After the model path is applied to the traffic graph,
some corrections in the scheduled hours can be made to adjust the prepared
transport offer to fit customer needs. Collision detection should then be
performed between that particular train and other trains running through the
network. The axis-aligned bounding box algorithm is used for this purpose [2]. If any collisions are found, they
should be eliminated, which is the actual routing of the train. With that
process, the appropriate level of traffic safety is ensured. The bees algorithm
is used in the process [26]. In this way, a timetable in
graphical form is obtained, which can be transformed into a tabular format.
The prepared timetable is passed for
approval to the railway carrier, who may accept or reject the proposal, in
whole or in part. If so, the timetable is passed back to the competent
construction and approval representatives. After introducing the corrections
and approving them, a notification of the assigned routes is given and the
timetable is implemented.
After obtaining the timetable, in the
case of both empty and loaded cars, a train should be formed and dispatched.
The transportation of loaded cars from the sender to the recipient can be
carried out according to the two transport technologies described in Section 3.
After arriving at the destination station, the set of cars is disassembled, with
the cars unloaded and remaining empty at the destination station, ready for
another loading.
4. CASE STUDY
The freight traffic
organization algorithms presented in Section 3 have been implemented in two
computer applications. The algorithm for the displacement of load and empty
cars (STAGE 1;
fig. 2) is the basis for
the ModPCar application. The timetable construction algorithm (STAGE 2;
fig. 2) is implemented in
the BEERJ application, which allows for the shaping of the railway transport
offer and the construction of traffic graphs, as well as presenting it in a
tabular format. An example of the applications’ output is shown in tab. 1.
Tab. 1
Sample output of ModPCar and BEERJ software
|
Plan for loaded cars |
Plan for empty cars |
||||||||||||||
|
Order number |
From
station |
Order number |
From
station |
Order number |
From
station |
Order number |
From station |
Order number |
From
station |
Order number |
From
station |
Order number |
From
station |
Order number |
From
station |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
1 |
ST_118 |
ST_59 |
0 |
42 |
Eaos |
17-02-04 13:20 |
17-02-06
12:00 |
17-02-08
02:19 |
17-02-09
09:24 |
1 |
17-02-04
12:35 |
17-02-04 13:20 |
ST_81 |
ST_118 |
42 |
|
2 |
ST_102 |
ST_85 |
0 |
42 |
Eaos |
17-02-06 11:00 |
17-02-06
12:00 |
17-02-07
19:59 |
17-02-10
11:27 |
2 |
17-02-06
10:42 |
17-02-06 11:00 |
ST_91 |
ST_102 |
42 |
|
3 |
ST_84 |
ST_123 |
0 |
10 |
Eaos |
17-02-07 03:01 |
17-02-07
04:00 |
17-02-07
19:08 |
17-02-10
02:16 |
3 |
17-02-07
02:25 |
17-02-07 03:01 |
ST_91 |
ST_84 |
10 |
|
4 |
ST_107 |
ST_1 |
0 |
40 |
Eaos |
17-02-07 03:01 |
17-02-07
04:00 |
17-02-08
05:16 |
17-02-09
01:18 |
4a |
17-02-07
02:10 |
17-02-07 03:01 |
ST_91 |
ST_107 |
37 |
|
4b |
17-02-07
03:01 |
17-02-07 03:01 |
ST_107 |
ST_107 |
3 |
||||||||||
In the sample case for the ModPCar software,
four customer orders have been included. In the left part of the table, the
proposed plan for loaded cars’ relocation is presented, separately for each
order. Columns 8 and 9 contain the most important customer requirements, i.e.,
the times of arrival and departure, which are not subject to change. At the
beginning of the analysis at each of these stations, there are not enough cars
to satisfy demand. In the first case, in order to fulfil the customer’s
request, empty cars must be delivered to the dispatch station as early as two
days in advance. In the second case, the buffer
is one day long, while, in the third case, it is only less than an hour
earlier. In the cases described above, all cars are delivered from one
station only. Order 4 represents a different situation. At station ST_107 (the
dispatch station for loaded cars), there are three empty cars. The rest should
be collected from the neighbouring station, ST_91.
The
hours in Columns 7, 10 and 12 were determined using the BEERJ application.
Based on the leading hours in Columns 8 and 9, reverse and forward routing were
performed, respectively, while model train paths were mapped onto the actual
traffic graph. In light of the collisions of proposed paths, they were
corrected and real train paths in time and space were obtained. For some
orders, the correction required to launch the trains was up to two days
earlier.
5. SUMMARY AND
CONCLUSIONS
The organization of railway traffic is a vital matter
to consider because it allows for trains to be managed on the railway network
in an orderly fashion, within the given time and space constraints. Its
introduction guarantees timely, fast, reliable and safe movement of rolling
stock. A train timetable is an expected outcome of correctly implemented
traffic organization, as it satisfies the requirements of various stakeholder
groups.
The organization of freight traffic on the railway
network consists of, on the one hand, the plans of cars’ movement prepared by
the operator (railway carrier) and, on the other hand, the rational
construction of timetables for trains being run: whether to move loaded or
empty cars. To introduce the correct form of traffic organization, one should
start by establishing which stations will become the supply of empty cars for
loading. This should be done, based on the cost minimization criterion. Car
delivery should occur before the time indicated by the customer, so that they
are ready for loading. Such functionality is provided by the ModPCar
application.
Afterwards, from the moment the loading ends, the
shipment should be completed as fast as possible. It is therefore important to
develop suitable timetables for a comprehensive transport service. When routing
the train, the leading hours indicated by the customer should be taken into
account, as well as the need to meet all safety requirements and avoid
collisions with existing train routes on the traffic graph. Such functionality is provided by the BEERJ application,
developed as an aid for designing the timetables according to the current needs
of the user.
References
1.
Albrecht Thomas.
2009. “Automated timetable design for demand-oriented service on suburban
railways.” Public Transport 1(1):
5-20. ISSN: 1866-749X. DOI: https://doi.org/10.1007/s12469-008-0003-4.
7.
Cordeau
Jean-François, Paolo Toth, Daniele Vigo. 1998. “A survey of optimization models
for train routing and scheduling.” Transportation
Science 32(4): 380-404. ISSN: 0041-1655.
8.
Hansen Ingo, Jörn
Pachl. 2008. Railway Timetable &
Traffic. Analysis, Modelling, Simulation. Hamburg: Eurailpress. ISBN 978-3-7771-0371-6.
17. Nowosielski Leopold. 1999. Organizacja Przewozów Kolejowych. [In Polish: Organization of Rail Transport.] Warsaw: Kolejowa Oficyna
Wydawnicza. ISBN: 83-86183-29-9.
19. PKP Polskie Linie Kolejowe S.A. 2015. Instrukcja o Prowadzeniu Ruchu Pociągów Ir-1
(R-1). [In Polish: Instruction on the
Conduct of Train Traffic Ir-1 (R-1).] Warsaw: PKP Polskie Linie Kolejowe S.A.
Received 12.03.2017; accepted in revised form 07.08.2017
![]()
Scientific Journal of Silesian
University of Technology. Series Transport is licensed under a Creative
Commons Attribution 4.0 International License
