Article citation information:
Grega, R., Homišin, J., Krajňák, J., Urbanský, M.: Analysis of the
impact of flexible couplings on gearbox vibrations. Scientific Journal of Silesian University of Technology. Series
Transport. 2016, 91, 43-50.
ISSN: 0209-3324. DOI: 10.20858/sjsutst.2016.91.4.
Robert GREGA[1],
Jaroslav HOMIŠIN[2],
Jozef KRAJŇAK[3],
Matej URBANSKÝ[4]
ANALYSIS OF THE IMPACT OF FLEXIBLE COUPLINGS ON GEARBOX
VIBRATIONS
Summary. Dangerous vibrations of mechanical
systems’ components are causes of failures and reduction in service life, as
well lead to negative effects on the environment and the health of
operators. In order to reduce these unwanted vibrations, it is necessary to pay
attention to the proper design of components in mechanical systems. The aim of
this article is based on the experimental measurements and demonstration of the
effects of different types of flexible couplings on the size of vibration in a
gearbox that forms part of a mechanical system.
Keywords: flexible couplings, vibrations,
gearbox, mechanical system
1. INTRODUCTION
In
mechanical systems, in which gear mechanisms are classified, unwanted vibrations
can be observed, for example, as a consequence of improperly designed,
manufactured, assembled and operated mechanical systems [1], [2], [3]. The main
issue regarding the reduction of vibrations concerns an intense flow of
information throughout the process of designing, manufacturing, installing, operating
and diagnosing mechanical systems. Responsibility for a low level of vibrations
cannot be delegated to a single designer, but should be owned by a team of
professionals. The fulfilment of all targets to minimize vibrations is in the
interests of those involved at the technical, legislative and subjective level.
It is very important to properly associate the aforementioned fields of
interest with the cost, durability and environmental impact of the measures
taken [10], [11], [12].
Knowledge
of the basic sources of excitation of vibration is one of the prerequisites for
enabling a reduction in vibrations within mechanical systems. It should be
remembered that, in addition to the known vibration exciters in vibration
spectra, random vibrations may occur that we cannot prejudge in advance. Such
random vibrations, however, could be an important source of information about
the technical condition of the mechanical system concerned [6], [7], [8], [9].
Torsional
vibrations represent a specific type of vibration, which are caused by the
rotating components. By assembling machinery that produces torsional vibrations
into a mechanical system, torsional vibrations follow the direction of energy
flow and in turn become vibration exciters to other parts of the system. In
many cases, serious failures are behind the cause of sources other than torsional
vibrations. It is very important to pay attention to machines that produce
torsional vibrations in order to minimize the impact of torsional vibrations within
a mechanical system. A very appropriate solution for vibration reduction in mechanical
systems is properly designed flexible shaft coupling. With properly designed
flexible coupling can help mechanical systems achieve a minimum level of
vibrations by appropriately tuning the revolutions produced by all members of
the system. In our case, the interest is directed to a gearbox, which forms
part of the examined mechanical system. Based on experimental measurements, we prove
the effect of different types of flexible couplings on the size of gearbox
vibration. In turn, we demonstrate the importance of appropriately tuning the mechanical
system using flexible coupling [4], [5].
2. EXPERIMENT DESCRIPTION
The experiment, which aimed to
demonstrate the impact of the flexible couplings on the size of gearbox
vibrations, was realized using the mechanical systems shown in Fig. 1. The
aforementioned mechanical system consisted of a torsional oscillation exciter,
which was a three-cylinder compressor. The compressor was driven by an
electromotor with the possibility of variable speed control. The examined
gearbox was included in the mechanical system between the compressor and the electromotor.
It was an auxiliary gearbox with the gear ratio i=1, as used in automotive drive.
The mechanical systems included other components necessary for diagnosing the
mechanical system.
The flexible couplings, which were used
during measurements, were included in sequence between the gearbox and the compressor.
Four types of coupling (shown in Fig. 2 to Fig. 5 inclusive) were examined:
pneumatic flexible coupling, Hardy coupling, Periflex coupling and claw
coupling.

Fig. 1 Scheme of the mechanical system

Fig. 2 Pneumatic flexible
coupling

Fig. 3 Hardy coupling

Fig. 4 Periflex coupling


Fig. 5 Claw coupling
3. EXPERIMENTAL MEASUREMENT RESULTS
The experiments were carried out in an operating mode with a rotation
speed between 200 min-1 and 1,000 min-1. In this
operating mode, the values of vibrations on the gearbox were obtained. The measured
value of the monitored vibrations, which is known as RMS, is regarded as an
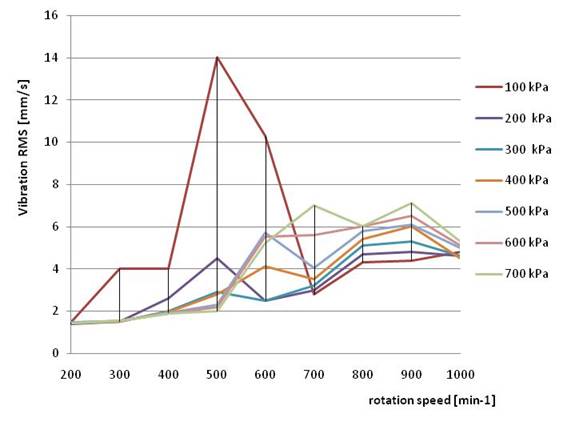
effective value of vibration speed. In the case of using pneumatic flexible
coupling to measure vibration values, air pressure between 100 kPa and 700 kPa,
in terms of pneumatic elements of coupling, were applied. In Fig. 6 to Fig. 9
inclusive, diagrams have been constructed based on the measurements of RMS on
the gearbox. As can be seen from the courses of RMS, the maximum value of the
vibration in each case is at a speed between 500 min-1 and 800 min-1.
This maximum value of RMS corresponds to the speed value when the mechanical system
starts to resonate from the main exciter’s harmonic component in the
compressor.
Fig. 6 Measured value of pneumatic flexible coupling
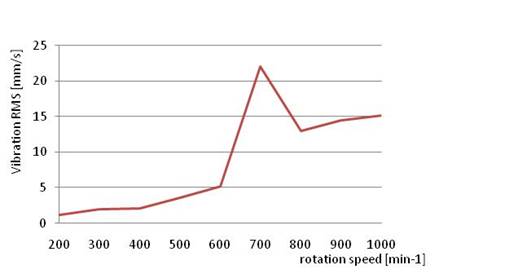

Fig. 7 Measured value of Hardy
coupling
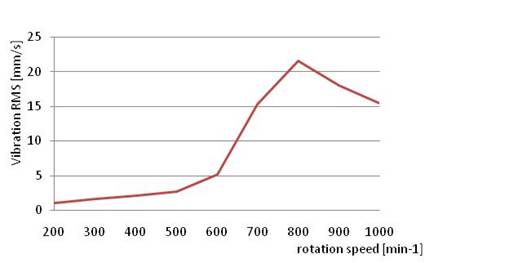

Fig. 8 Measured value of Periflex
coupling
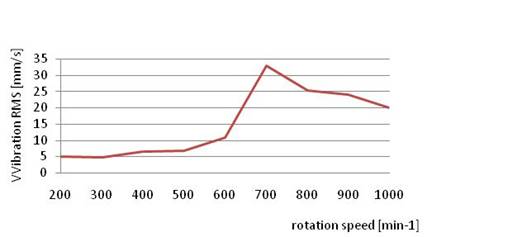

Fig. 9 Measured value of claw
coupling
4. CONCLUSION
Following the mutual
comparison of the individual values of vibrations obtained from the measurements,
we can state that, in the current case regarding all operating speeds of the
mechanical system, the lowest vibration levels in a gearbox are achieved using pneumatic
flexible couplings with a pressure of 300 kPa in their pneumatic flexible
elements.
Fig. 10 presents all
RMS courses of each of the used couplings. The RMS course, which uses pneumatic
flexible coupling, represents the line with a value of air pressure equal to 300
kPa. As stated in this figure, we can observe that the size of vibration
involving pneumatic flexible coupling equates to less than 700% in comparison
with other couplings, especially in the area of resonance of
the mechanical system. The aforementioned target detections, therefore, represent
sufficient grounds to present our proposals for an appropriate coupling design
for any mechanical system. In particular, the suitability of selected
flexible coupling can significantly protect individual parts of
the mechanical system and thus increase their durability, as well as
reduce their failure rate.
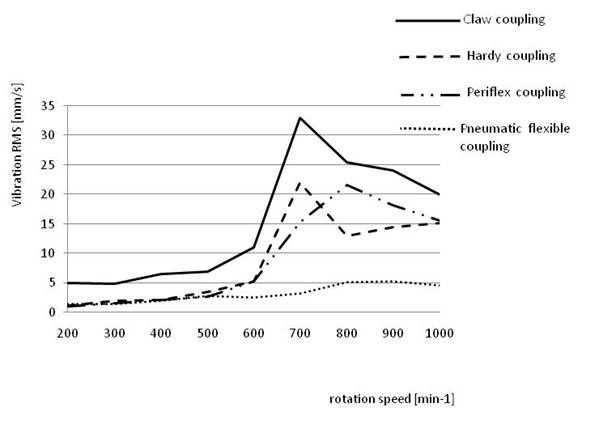

Fig. 10 Measured value of all used
couplings
References
1.
Grega
R. et al. 2015 „The chances for reduction of vibrations in mechanical system
with low-emission ships combustion engines”. International Journal of Maritime
Engineering 157 (A4): 235-240. ISSN: 1479-8751.
2.
Baran P., R. Grega.
2015. „Comparison of dynamic properties of dual mass flywheel”. Diagnostyka
16(1): 29-33. ISSN: 1641-6414.
3.
Medvecká-Beňová
S., M. Mantič, R. Grega. 2014. „The stress
analysis in dangerous section of gear teeth”. Applied Mechanics
and Materials 611: 279-283.
ISSN: 1660-9336.
4.
Homišin J. 2013. „New ways of controlling dangerous torsional
vibration in mechanical systems”. Transactions on Electrical Engineering 2(3):
70-76.
ISSN: 1805-3386.
5.
Homišin J., P. Kaššay, P. Čopan. 2014. „Possibility of torsional
vibration extremal control”. Diagnostyka
15(2): 7-12. ISSN: 1641-6414.
6.
Vaško
M., B. Leitner, M. Sága. 2010. „Computational fatigue
damage prediction of the lorry frames under random excitation”. Communications
12(4): 62–67.
ISSN: 1335-4205.
7.
Sága M., P. Kopas,
M. Vaško. 2010. „Some computational aspects of vehicle shell frames
optimization subjected to fatigue life”. Communications 12(4): 73-79.
ISSN: 1335-4205.
8.
Konieczny Ł., R.
Burdzik, J. Warczek, P. Czech, G. Wojnar, J. Młyńczak. 2015. „Determination of the effect of tire stiffness on wheel accelerations by
the forced vibration test method”. Journal of Vibroengineering 17(8):
4469-4477.
ISSN: 1392-8716.
9.
Dekys
V., A. Sapietova, O. Stevka. 2013. „Understanding of the
dynamical properties of machines based on the interpretation of spectral
measurement and FRF”.
In 51st International
Scientific Conference on ”Experimental Stress analysis”: 106-112. Litomerice, Czech Republic. 11-13 June
2013.
10.
Jakubovičová L., P. Zavadinka, J. Jakubovič. 2016. „Transport duty cycle measurement of hybrid
drive unit for mixing drum”. Advances in
Intelligent Systems and Computing 393: 219-224. Berlin: Springer Verlag. ISSN:
21945357.
11.
Wojnar G., P. Czech, P. Folęga. 2014. „Problem with diagnosing local faults of gearboxes on the basis of vibration
signal”. Transactions of the Universities
of Košice 2: 95-100. ISSN: 1335-2334.
12.
Czech
P., G. Wojnar, J. Warczek. 2014. „Diagnosing of car engine fuel injectors
damage using bi-spectral analysis and radial basis function.” Logistyka 3: 1,181-1,187.
ISSN: 1231-5478.
This paper was written under the framework of Grant
Project VEGA: “1/0688/12 – Research on and application of a universal
regulation system in order to master the source of mechanical systems’
excitation”.
Received 21.11.2015; accepted in revised form 11.04.2016
![]()
Scientific Journal of Silesian University of
Technology. Series Transport is licensed under a Creative Commons
Attribution 4.0 International License