Article citation information:
Drewniak, J., Garlicka, P., Kolber, A. Design for the bi-planetary gear
train. Scientific Journal of Silesian
University of Technology. Series Transport. 2016, 91, 5-17. ISSN: 0209-3324. DOI: 10.20858/sjsutst.2016.91.1.
Józef DREWNIAK[1],
Paulina GARLICKA[2],
Aleksandra KOLBER[3]
DESIGN FOR A BI-PLANETARY GEAR
TRAIN
Summary. The
article presents the design for a bi-planetary gear train. The project
description is supplemented with calculations of kinematics, statics and meshing
efficiency of the gear wheels included in the gear train. Excluded are calculations
of strength and geometry of gears, shaft and rolling bearing, since they are
similar to classical calculations for planetary gears. An assembly drawing in
2D and assembly drawings in 3D of the designed bi-planetary gear train are also
shown. This gear train will form the main element of the research in hand.
Keywords: bi-planetary gear train, transmission
ratio, meshing efficiency
1. INTRODUCTION
The structural diagram of a bi-planetary
gear train, or double planetary gear train, is shown in Fig. 1a and Fig. 2
[1]. It consists of a main planetary gear set and an internal planetary gear
set, which is known as an internal satellite system. The main planetary gear
set comprises sun gear 1, satellites 2 and 6, external carrier arm h and ring
gear 7, which is fastened to the frame, while the internal satellite system comprises
sun gear 3, satellites 4 with internal carrier arm H, and ring gear 5, which is
fastened to carrier arm h. In the bi-planetary gear train, the role
of second toothed satellite 6 (Fig. 1b) fulfils the needs of the planetary
gear train, known as the internal satellite system, with carrier arm H. H
drives planetary gear 6, which already belongs to the main gear set. At
the same time, rim gear 5 drives carrier arm h of the main planetary gear
set.
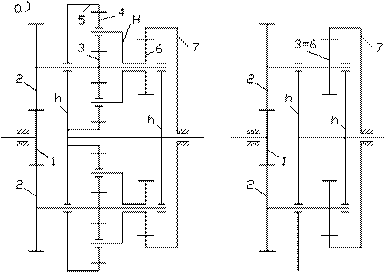
Fig. 1. Kinematic
diagrams of the bi-planetary and planetary gear trains [1]
A characteristic feature of this
gear train is that the satellites within the satellite mechanism rotate around
three axes – those of its own central planetary gear set and the main central bi-planetary
gear train. This particular property of bi-planetary gear train is mainly used
in face milling cutters for combined mining.
2. DESIGN CALCULATIONS
2.1. Kinematic diagram of the gear
The structure of the transmission is
selected depending on the kinematic ratio. The values of output torque are
equal to ![]() and
and ![]() , respectively, when the value of input revolution is equal
to
, respectively, when the value of input revolution is equal
to ![]() .
.
For the required range of output
speed ![]() , the mean transmission ratio and the acceptable range of
ratios are:
, the mean transmission ratio and the acceptable range of
ratios are:
![]() , (1)
, (1)
![]() .
(2)
.
(2)
On basis that the demands correspond
to the planetary gear, the kinematic diagram, as shown in Fig. 2, is according
to [2, 3, 9].
This gear comprises the inner transmission
(satellite planetary mechanism) of 3, 4, 5, H and of the outer transmission of 1,
2, 6, 7, h.
The degree of mobility of the
transmission is:
![]() (3)
(3)
where ![]() ( number of moving parts);
( number of moving parts); ![]() (number of pairs of 5-class (arm h on the right is oversized
or redundant)); and
(number of pairs of 5-class (arm h on the right is oversized
or redundant)); and![]() (number of pairs 4-class (engagement of teeth, counted only
once)).
(number of pairs 4-class (engagement of teeth, counted only
once)).
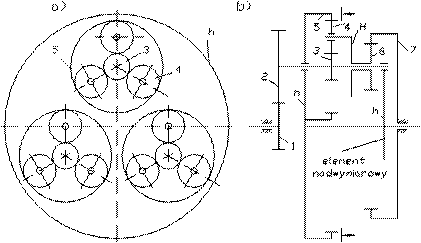
Fig. 2. Kinematic diagram of the bi-planetary
gear train
As the degree of mobility is ![]() , only one value of a speed output or input is needed to
determine the speed of each of the transmission components.
, only one value of a speed output or input is needed to
determine the speed of each of the transmission components.
2.2. Gear transmission ratio
According to the definition of the
kinematic gear ratio, ![]() (from pinion 1 to arm
(from pinion 1 to arm ![]() , when wheel 7 is fixed) is equal to [1, 3, 4, 5, 6, 7]:
, when wheel 7 is fixed) is equal to [1, 3, 4, 5, 6, 7]:
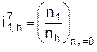 ,
(4)
,
(4)
where ![]() (the rotational speed
of pinion 1 or input rotational speed of transmission) and
(the rotational speed
of pinion 1 or input rotational speed of transmission) and ![]() (the rotational speed
of arm
(the rotational speed
of arm ![]() , that is, the transmission output rotational speed) (Fig. 1).
In order to determine the kinematic ratio,
, that is, the transmission output rotational speed) (Fig. 1).
In order to determine the kinematic ratio, ![]() must first determine
the base ratio of the inner transmission, assuming that
the whole planetary gear rotational speed is equal to
must first determine
the base ratio of the inner transmission, assuming that
the whole planetary gear rotational speed is equal to ![]() (that is, to consider
the kinematics of planetary transmission in relation to arm
(that is, to consider
the kinematics of planetary transmission in relation to arm ![]() ). Then, the relative rotational speed of each wheel gear is equal
to
). Then, the relative rotational speed of each wheel gear is equal
to ![]() (
(![]() ) at the same time that
) at the same time that ![]() and
and ![]() (because
(because ![]() and
and ![]() ).
).
Similarly, the relative rotational speed
of inner arm H, in relation to external arm h, is ![]() . The basic kinematic ratio of the inner transmission, which consists
of wheels 3, 4, 5 and arm H with known relative speed
. The basic kinematic ratio of the inner transmission, which consists
of wheels 3, 4, 5 and arm H with known relative speed ![]() ,
, ![]() ,
, ![]() and
and ![]() , can be determined using the Willis formula (5) and
expression (6) for the transmission ratio of wheels 3, 4 and 5, in relation to
arm H as a function of the number of teeth (such as for the gears with
fixed axes) [1]:
, can be determined using the Willis formula (5) and
expression (6) for the transmission ratio of wheels 3, 4 and 5, in relation to
arm H as a function of the number of teeth (such as for the gears with
fixed axes) [1]:
![]() (5)
(5)
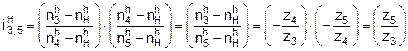 (6)
(6)
Hence:
![]() ,
(7)
,
(7)
because ![]() .
.
To calculate the requested transmission
ratio of the bi-planetary gear train, it is firstly
necessary to determine unknown relative rotational speeds ![]() and
and ![]() using formula (7)
above, as a function of
using formula (7)
above, as a function of ![]() (9) and
(9) and ![]() of the two conditions
on the gear ratios
of the two conditions
on the gear ratios ![]() (8) (the ratio from arm
H to wheel 7) and
(8) (the ratio from arm
H to wheel 7) and ![]() (10) (the ratio from
wheel 3 to wheel 1):
(10) (the ratio from
wheel 3 to wheel 1):
![]() , (8)
, (8)
Hence
![]() , (9)
, (9)
because ![]() .
.
Similarly,
![]() , (10)
, (10)
Hence
![]() , (11)
, (11)
because ![]() and
and ![]() .
.
Thus, after the subsequent
transformations, the quotient of the number of teeth ![]() , according to formula (7), takes the following form (12):
, according to formula (7), takes the following form (12):
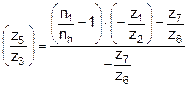 . (12)
. (12)
Hence the formula for the ratio of
the bi-planetary gear train (4) is as follows:
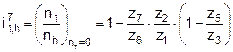 (13)
(13)
The required value of the ratio
obtained for the numbers of teeth of the bi-planetary gear train – namely,![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , is due to the following:
, is due to the following:
![]() , (14)
, (14)
That is, ![]() .
.
The actual
value of the output speed is ![]() .
.
2.3. Engagement efficiency of the transmission
Determining the efficiency of the
gear train only takes into consideration the losses incurred due to friction in
the gear engagements, i.e., it does not include the friction that occurs
between the bearings and the resistance of the splashing oil. Thus, according
to formula (15), the efficiency of the designed bi-planetary gear train only depends
on the base kinematic ratio ![]() of the transmission
and the base efficiency
of the transmission
and the base efficiency ![]() [1, 6, 7]:
[1, 6, 7]:
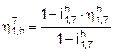 .
(15)
.
(15)
The base efficiency is determined in
relation to the serial sequence composed of the pair of wheels 1 and 2, planet
gears 3, 4 and 5, and the last pair of wheels 6 and 7:
![]() .
(16)
.
(16)
The efficiency of the pair of outer
wheels 1 and 2, when considered in motion relative to arm h, is determined by the
following known formula [3, 6]:
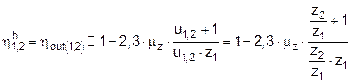 (17)
(17)
A similar formula determines the
efficiency of the pair of inner wheels 6 and 7, when considered in motion
relative to arm h [2, 3, 5, 6]:
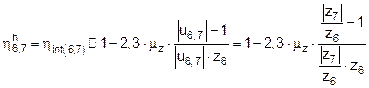 .
(18)
.
(18)
The base efficiency for the internal
epicyclic gearing of 3, 4, 5 and H is determined by the following formula
[2, 3, 5, 6]:
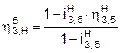 ,
(19)
,
(19)
where ![]() (see formula (7)) and
(see formula (7)) and ![]() are the base transmission ratio and the base efficiency of
the inner epicyclic transmission of 3, 4, 5 and H, respectively:
are the base transmission ratio and the base efficiency of
the inner epicyclic transmission of 3, 4, 5 and H, respectively:
![]() (20)
(20)
where![]() (base efficiency of wheels 3 and 4).
(base efficiency of wheels 3 and 4).
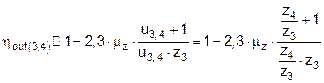 ,
(21)
,
(21)
where![]() (base efficiency of wheels 4 and 5).
(base efficiency of wheels 4 and 5).
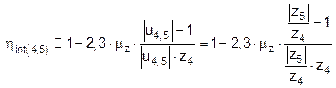 .
(22)
.
(22)
Component values of the base efficiency
for the assumed value of the coefficient of friction in engagement ![]() are:
are:
![]() ,
, ![]()
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Thus, the efficiency of the
planetary gear is:
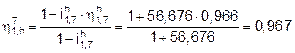 , (23)
, (23)
because:
![]()
And:
![]() .
.
The value of efficiency of the bi-planetary
gear unit is similar to the value of efficiency of the three-axes non-planetary
gear train (![]() ), although it is greater than the efficiency value of the
planetary gear, even when the transmission ratio is of less value.
), although it is greater than the efficiency value of the
planetary gear, even when the transmission ratio is of less value.
2.4. Forces acting on the spur gear teeth
According to the principle of the operation
of the bi-planetary gear train, the output torque ![]() consists of three
components:
consists of three
components:
a) Torque ![]() generated by
generated by ![]() satellite 2 [1, 2]:
satellite 2 [1, 2]:
![]() ,
(24)
,
(24)
where ![]() (the force acting on
the axis of satellite 2) (Fig. 3);
(the force acting on
the axis of satellite 2) (Fig. 3); ![]() ,
, ![]() (the pitch radiuses of sun gear 3 and the satellite 2)’; and
(the pitch radiuses of sun gear 3 and the satellite 2)’; and ![]() (the radius of carrier arm h).
(the radius of carrier arm h).
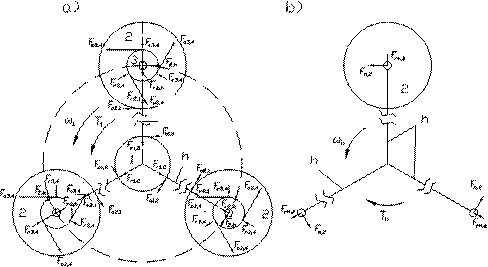
Fig. 3. The forces acting during the engagement
of gears 1, 2, 3 and on left arm h
b) Torque ![]() generated by
generated by![]() rim gear wheel 5 (Fig. 3, Fig. 4):
rim gear wheel 5 (Fig. 3, Fig. 4):
![]() , (25)
, (25)
where ![]() ,
, ![]() (the pitch radiuses of
sun gear 3 and rim gear 5); and
(the pitch radiuses of
sun gear 3 and rim gear 5); and ![]() (the circumferential
force acting on gear 5).
(the circumferential
force acting on gear 5).
c) Torque ![]() generated by
generated by![]() carrier arm H and satellite 6 (Fig. 5):
carrier arm H and satellite 6 (Fig. 5):
![]() , (26)
, (26)
where![]() (the pitch radius of satellite 6); and
(the pitch radius of satellite 6); and ![]() (the force acting on
the axis of satellite 6).
(the force acting on
the axis of satellite 6).
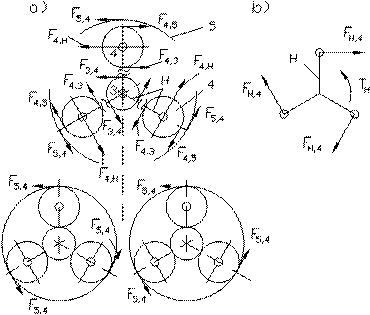
Fig. 4. The forces acting during the engagement
of gears 3, 4, 5 and on arm H
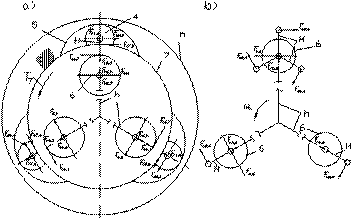
Fig. 5. The forces acting during the engagement
of gears 6, 7 and on right arm h
As such, total output torque ![]() is equal to:
is equal to:
![]() . (27)
. (27)
Total output torque ![]() , with regard to engagement efficiency
, with regard to engagement efficiency ![]() , is equal to:
, is equal to:
![]() .
(28)
.
(28)
3. DESIGN BI-PLANETARY GEAR TRAIN
3.1. Description of the gear train
As previously mentioned in this
paper, the bi-planetary gear train consists of two planetary drive systems,
i.e., the outer gear set, also known as the main gear set, and the inner gear
set, which is known as a satellite planetary system. The main planetary gear
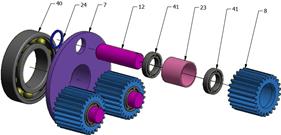
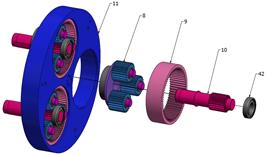
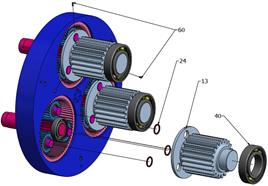
set consists of sun gear 3, which meshes with the three satellites 4 mounted on
three shafts, namely, pinions 10 of the satellite planetary system (Fig. 6). Pinions
10 represent the sun gear of the planetary satellite system. It drives the three
satellites 8, which are still engaged with the gear wheel due to internal teeth
9 being fitted to one of the three holes of arm 11. Each satellite is mounted
rotationally on axle 12, on which is supported one of the three internal arms H
(according to Fig. 1). Each arm H is a part of second satellite 13, which
already belongs to the main gear set.
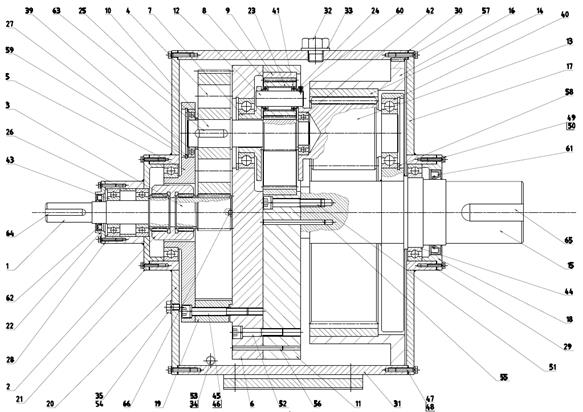
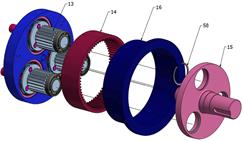
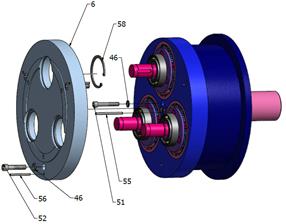
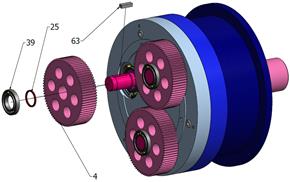
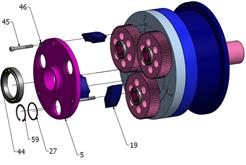
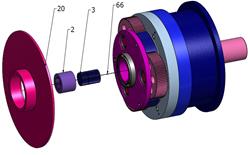
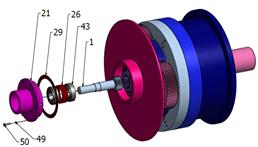
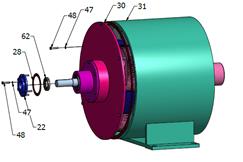
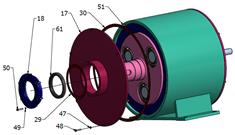
Fig. 6. Assembly engineering drawing
of the bi-planetary gear train
Satellite
13 is meshed with fixed internal gear wheel 14 and internally mounted on the
right side of the hole in arm 11 of output shaft 15. Power is transmitted from
the electric motor via shaft 1 and clutch 2 to sun gear 3, which is
engaged with the three satellites 4 mounted on shaft 10 that transmits part of
the torque along intermediate arm 11, then along output shaft 15, while the
rest of the power is transmitted through gear wheel 9 to arm 11, then through
internal arm 7 (satellite 13) to right arm 11.
3.2. The order of the assembly
of the bi-planetary gear train elements
Engineering drawings of the assembly
sequence, which allow for checking the correctness of the designed bi-planetary
gear trains (Fig. 6) in terms of mounting options and possibly assessing its
degree of difficulty, are included in Table 1.
Tab. 1.
Engineering drawings of the assembly
sequence
|
a)
|
b)
|
|
c)
|
d)
|
|
e)
|
f)
|
|
g)
|
h)
|
|
i)
|
j)
|
|
k)
|
Note: not shown is the sequence of
the assembly of simple elements, such as oil filler plugs, oil level and oil
drain plug. |
4. CONCLUSION
This paper presents the design of a bi-planetary
gear train together with the calculation of the kinematics, statics and
meshing efficiency of gear wheels. Omitted from the calculation are the geometry
and strength of gears, shafts and rolling bearings, as these are recognized as
being typical design calculations. 3D drawings of the order of assembly
components have confirmed the correctness of the design of the bi-planetary
gear train. The designed planetary gear is constructed as a prototype for transmission
to the test bench in a laboratory for fundamental machine design. The main aim
of this study is in comparing the dynamics of the transmission between fastened
rim wheel 14 and the solution, when wheel 14 is suspended flexibly from the
coupling gear (variant II of the solution).
References
1.
Cyplakow
Ju.S. 1968. Biplanetarnye mechanizmy.
[In Russian: Bi-planetary Mechanisms].
Moscow: Mas’inostroenie.
2.
Drewniak J. 2000. Zbiór zadań z PKM III. [In Polish: The Set of Tasks from
PKM III]. Bielsko-Biała: ATH.
3.
Kudriawcew
W.N., Ju.N. Kirdiaszew (red.). 1977. Planetarnye
peredaczi. [In Russian: Planetary Peredaktsi].
Leningrad: Mas’inostroenie.
4.
Looman
J. 1988. Zahnradgetriebe. [In German:
Gear Transmission]. Berlin:
Springer-Verlag.
5.
Mueller
H.W. 1971. Die Umlaufgetriebe. [In German: The Epicyclic Gear]. Berlin: Springer Verlag.
6.
Mueller L., A. Wilk. 1996. Zębate przekładnie
obiegowe. [In
Polish: Toothed Planetary Gears]. Warsaw:
PWN.
7.
Rudenko W.N. 1980. Planetarnye i wolnowye
peredaci. [In
Russian: Planetary and Wave Transmission].
Moscow: Mas’inostroenie.
8.
Homišin J. 2008. Dostrajanie układów mechanicznych drgających skrętnie przy pomocy sprzęgieł
pneumatycznych: kompendium wyników pracy naukowo-badawczych. [In Polish: Tuning Torsionally Vibrating Mechanical Systems
using Pneumatic Couplings: A Compendium of Performance Research]. Bielsko-Biała:
ATH.
ISBN: 978-83-60714-55-3.
9.
Homišin
J., P. Kaššay, P. 2009. „Comparison of tuning in shipping system using pneumatic tuners of
torsional oscillations”. Machine modeling and simulations:
147-154. ISBN 978-80-89276-18-9.
10.
Grega
R., J. Krajňák. 2012. „The pneumatic dual-mass flywheel”. Scientific Journal of Silesian University of
Technology. Series Transport 76: 19-24. ISSN: 0209-3324.
11.
Grega
R. et al. 2015 „The chances for reduction of vibrations in mechanical system
with low-emission ships combustion engines”. International Journal of Maritime
Engineering 157 (A4): 235-240. ISSN 1479-8751.
12.
Homišin
J., P. Kaššay, M. Urbanský. 2011. „High-flexibility characteristics of
pneumatic flexible shaft couplings”. Pneumatyka 79(2): 26-29. ISSN 1426-6644.
13.
Medvecká-Beňová
S., J. Krajňák. 2015. „Modifications to a gearbox to increase the performance
of a winding machine for steel sheets.” IT-strojár: 1-3.
ISSN 1338-0761.
14.
Bigoš
P., J. Kuľka, M. Mantič, M. Kopas. 2015. „Comparison of local stress values
obtained by two measuring methods on a blast furnace shell”. Metalurgija
54(1):
101-104. ISSN 0543-5846.
15.
Grega
R., J. Krajňák. 2013. „The application of pneumatic flexible coupling in a conveyor drive”. Technológ
5(4): 51-54. ISSN 1337-8996.
16.
Medvecká-Beňová
S., J. Vojtková. 2014. „Application of an asymmetric profile in gearings with eccentric gears”. Scientific Journal of Silesian University of
Technology. Series Transport 85: 89-93. ISSN: 0209-3324.
17.
Kuľka
J., M. Mantič. 2014 „Effect of operational condition changes on the durability of the rope
for pusher of circular wagon tipper”. Applied
Mechanics and Materials 683: 28-32. ISSN 1660-9336.
18.
Homišin
J., M. Urbanský. 2015. „Partial results of extremal control of mobile mechanical system”. Diagnostyka 16(1): 35-39. ISSN
1641-6414.
Received 20.12.2015;
accepted in revised form 27.04.2016
![]()
Scientific Journal of
Silesian University of Technology. Series Transport is licensed under a Creative
Commons Attribution 4.0 International License