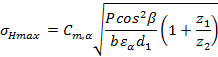Article citation info:

Batsch, M. Surface strength of Novikov convexo-concave gears. Scientific Journal of Silesian University of Technology. Series Transport. 2016, 90, 17-24. ISSN: 0209-3324. DOI: 10.20858/sjsutst.2016.90.2.

 

 

Michał BATSCH[1]

 

 

 

SURFACE STRENGTH OF NOVIKOV CONVEXO-CONCAVE GEARS

 

Summary. Article presents the algorithm for obtaining maximum surface stresses for Novikov gears. Described surface strength calculation method is based on  Hertz theory of two bodies being in point contact. What’s more the influence of gear position errors on maximum contact stresses has been presented. Also the comparison of Hertz stresses for Novikov and involute gears has been made.

Keywords: surface strength, Novikov convexo-concave gear, Hertz theory, deviation

 

 

 

NOŒNOŒĆ POWIERZCHNIOWA PRZEKŁADNI ZĘBATYCH O KOŁOWO-ŁUKOWYM ZARYSIE ZĘBÓW TYPU NOWIKOWA

 

Streszczenie. Artykuł przedstawia algorytm wyznaczania maksymalnych naprężeń stykowych dla przekładni zębatych typu Nowikowa. Opisywana metoda obliczeń wytrzymałoœciowych na naciski opiera się na zastosowaniu klasycznej teorii Hertza dla styku punktowego dwóch dowolnych ciał. Ponadto przedstawiono wpływ błędów położenia osi kół przekładni na wielkoœć nacisków powierzchniowych. Dokonano również porównania naprężeń uzyskanych w wyniku zastosowania wzorów Hertza dla przekładni Nowikowa i ewolwentowej.

Słowa kluczowe: noœnoœć powierzchniowa, przekładnia zębata Nowikowa o kołowo-łukowym zarysie zębów, teoria Hertza, odchyłki

1.    WPROWADZENIE

 

W artykule opisano metodę pozwalajšcš na wyznaczenie naprężeń stykowych kół przekładni Nowikowa. Metoda ta bazuje na klasycznym podejœciu, opartym na teorii Hertza [2], z którego korzystano w pracach [1, 4]. Ponadto wyznaczono wpływ błędów montażu przekładni na wielkoœć nacisków powierzchniowych oraz porównano wytrzymałoœć stykowš przekładni Nowikowa z wytrzymałoœciš stykowš przekładni ewolwentowej.

 

 

2.  Wyznaczanie naprężeń stykowych wg Hertza

 

     Styk zębów przekładni Nowikowa jest punktowy. Pod wpływem działania sił zęby odkształcajš się, a styk odbywa się na pewnej powierzchni, zazwyczaj ograniczonej elipsš. Niniejszy rozdział stanowi opis toku postepowania w przypadku wyznaczania naprężeń stykowych wg Hertza dla punktowego styku zębów przekładni Nowikowa.

W celu wyznaczenia naprężeń należy rozważyć dwie stykajšce się powierzchnie, pokazane na rysunku 1.

 

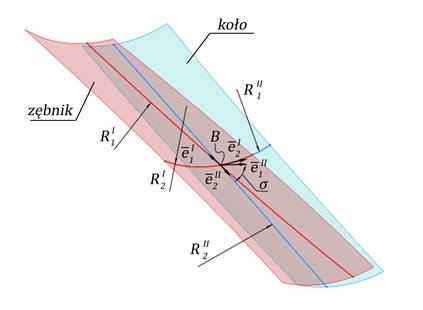
Rys. 1. Styk punktowy powierzchni bocznych zębów przekładni Nowikowa

 

     Stykajšce się powierzchnie opisane sš za pomocš głównych promieni krzywizn. Kšt  jest to kšt pomiędzy odpowiednimi kierunkami głównymi powierzchni. W otoczeniu punktu styku B stykajšce się powierzchnie można opisać paraboloidami o równaniach [1]:

 

(1)

(2)

 

gdzie:

,  – odpowiednio promienie krzywizn głównych − pierwszej i drugiej − powierzchni bocznej zęba zębnika,

,  – promienie krzywizn głównych − pierwszej i drugiej − powierzchni bocznej zęba koła.

 

     Odległoœć pomiędzy powierzchniami mierzona wzdłuż osi z, pokrywajšcej się ze wspólnš, normalnš obydwu powierzchni wyraża się wzorem:

 

          (3)

 

     Osie układu współrzędnych obiera się tak, aby współczynnik C przyjšł wartoœć zero. Jest to spełnione, gdy:

 

          (4)

 

     Rozwišzujšc układ równań (4) można wyznaczyć współczynniki A i B w postaci (5)

 

(5)

 

     Wówczas odległoœć pomiędzy powierzchniami wyraża się wzorem (6):

 

,

          (6)

 

gdzie

 to główne, względne promienie krzywizn.

 

     Dla tak opisanej, w otoczeniu punktu styku, geometrii rozkład naprężeń jest półelipsoidš o równaniu (7):

 

,

          (7)

gdzie:

ae, be – to odpowiednio mała i wielka osie elipsy styku,

 – maksymalne naprężenia stykowe.

 

     Parametry obszaru styku ae i be okreœla się rozwišzujšc równanie (8):

 

,

          (8)

 

gdzie:

K(e) – zupełna całka eliptyczna drugiego rodzaju,

E(e) – zupełna całka eliptyczna pierwszego rodzaju,

 – argument całki.

 

     Równanie (8) można rozwišzać numerycznie, np. metodami Newtona lub bisekcji. Po jego rozwišzaniu znany jest stosunek wielkiej osi elipsy styku do osi małej be/ae. Następnie, wykorzystujšc zależnoœć (9) oblicza się oœ wielkš elipsy styku:

 

,

          (9)

 

gdzie:

Re – równoważny promień krzywizny okreœlony zależnoœciš (10)

 

,

          (10)

 

gdzie:

F1(e) − współczynnik zależny od stosunku be/ae, wyrażony wzorem (11)

 

,

          (11)

 

gdzie:

E* − zastępczy moduł Younga, okreœlony równaniem (12)

 

,

          (12)

 

gdzie:

E1, E2 – moduły Younga materiału odpowiednio zębnika i koła,

ν1, ν2 – współczynniki Poissona materiału odpowiednio zębnika i koła.

 

     Znajšc stosunek osi wielkiej do osi małej elipsy styku, wyznaczony jako rozwišzanie równania (8), oraz oœ wielkš, okreœlonš równaniem (9) można wyznaczyć oœ małš jako (13):

 

          (13)

 

Maksymalne naprężenia występujšce w punkcie styku okreœla zależnoœć (14):

 

 ,

          (14)

 

gdzie P to siła obwodowa.

 

     Z uwagi na przetaczanie się punktu styku i poskokowy wskaŸnik przyporu siła ta zmienia swojš wartoœć. Zatem dla przekładni o poskokowym wskaŸniku przyporu mieszczšcym się
w granicach od 1 do 2 w celu obliczenia naprężeń stykowych w połowie szerokoœci wieńca we wzorze (14) należy przyjšć nominalnš maksymalnš wartoœć siły obwodowej. Siła ta jest wówczas przenoszona przez jeden zšb. W przypadku innego położenia punktu styku siła obwodowa może być przenoszona przez dwa zęby, wówczas można jš zmniejszyć dwa razy.

 

 

3.  Wpływ błędów montażu przekładni na wielkoœć naprężeń stykowych

 

     Jak wynika z przeprowadzonej analizy styku zębów przekładni Nowikowa [3], w której uwzględniono błędy położenia osi, punkt styku zmienia swoje położenie na powierzchni bocznej zęba w stosunku do swojego położenia dla przekładni bezodchyłkowej. Zmieniajš się wówczas krzywizny oraz kierunki główne w punkcie styku, które sš zależne od parametrów powierzchni, definiujšcych położenie tego punktu. Wobec powyższego można się spodziewać zmiany wielkoœci nacisków powierzchniowych. Aby je wyznaczyć, należy zastosować metodę Hertza (opisanš w rozdziale 2) z wykorzystaniem nowych, głównych promieni krzywizn i nowego kšta pomiędzy kierunkami głównymi powierzchni. Wielkoœci te wyznacza się z wykorzystaniem parametrów powierzchni, uzyskanych w wyniku analizy styku zębów, która uwzględnia błędy położenia osi przekładni.

     Rysunek 2 przedstawia wpływ błędu rozstawienia osi kół na wielkoœć nacisków powierzchniowych dla przykładowej przekładni Nowikowa, obcišżonej momentem obro-towym M1=550 Nm.

     W przypadku uwzględnienia jedynie błędu rozstawienia osi kół, naciski sš takie same na całym obszarze ruchu punktu styku. Im błšd ten zwiększa się, tym naciski stajš się mniejsze. Zjawisko to można wyjaœnić spadkiem rzeczywistego kšta przyporu, a co za tym idzie –przesunięciem się punktu styku ku stopie zęba zębnika, gdzie zmniejsza się stosunek œrednich głównych promieni krzywizn. Przy projektowaniu przekładni Nowikowa należy uwzględnić błšd rozstawienia osi oraz celowo zwiększyć kšt przyporu lub stosunek promienia zarysu zębnika do jego promienia podziałowego, co pozwala na zmniejszenie naprężeń stykowych oraz kontrolę nad położeniem obszaru styku. Należy również zaznaczyć, że zbyt duży błšd rozstawienia osi może w efekcie prowadzić do zwiększenia naprężeń, w wyniku ich koncentracji spowodowanej krawędziowaniem œladu styku.

 

 

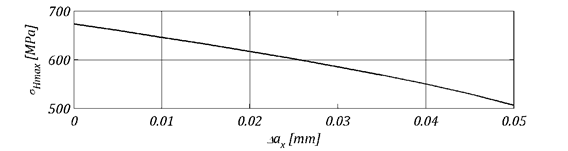
napr-dax

 

Rys. 2. Zależnoœć nacisków powierzchniowych od błędu rozstawienia osi

 

     Na rysunku 3 przedstawiono wpływ błędu przekoszenia osi dla symetrycznego położenia przekładni względem podpór.

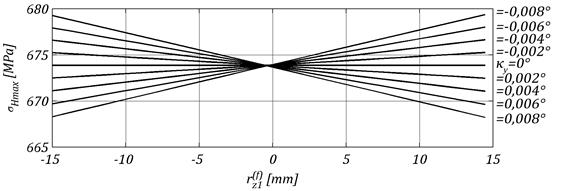
napr-kappay

 

Rys. 3. Zależnoœć nacisków powierzchniowych od położenia punktu styku
oraz błędu przekoszenia osi

 

     Naciski zwiększajš się lub zmniejszajš w zależnoœci od znaku kšta , poczšwszy od wejœcia w zazębienie aż do wyjœcia z zazębienia.

 

 

4.  Porównanie naprężeń stykowych przekładni ewolwentowej oraz Nowikowa

 

     W niniejszym rozdziale porównano teoretyczne naprężenia wg Hertza dla przekładni ewolwentowej oraz Nowikowa. Naprężenia stykowe dla przekładni Nowikowa obliczono w połowie szerokoœci wieńca metodš z rozdziału 2., bez uwzględnienia błędów położenia osi. Naprężenia dla przykładowej przekładni ewolwentowej wyznaczono bazujšc na znanym wzorze (15) [6, 5].

 

          (15)

 

     Rysunek 4 przedstawia zależnoœci naprężeń Hertza od momentu obcišżajšcego zębnik dla przekładni ewolwentowej oraz Nowikowa o tych samych parametrach.

 

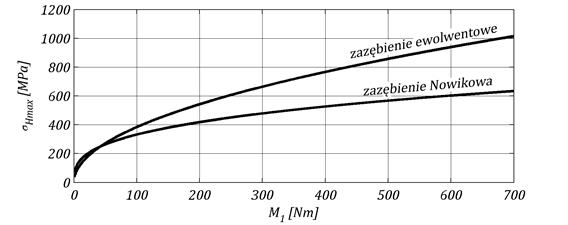
napr_od_mom

Rys. 4 Porównanie naprężeń Hertza przekładni ewolwentowej oraz Nowikowa

 

     Dla małych obcišżeń zazębienie ewolwentowe wykazuje większš noœnoœć na naciski aniżeli zazębienie Nowikowa. Dla obydwu przekładni naprężenia sš równe dla momentu M1=42 Nm. Powyżej tej wartoœci teoretyczna noœnoœć zazębienia Nowikowa w porównaniu do ewolwentowego znaczšco roœnie. Dla momentu M1=480 Nm naprężenia w przekładni o zarysie Nowikowa sš 1,5 razy mniejsze niż w przekładni o zarysie ewolwentowym. Wynika stšd fakt, że zazębienie Nowikowa będzie opłacało się stosować dla przekładni silnie obcišżonych, gdzie wytrzymałoœć stykowa odgrywa największš rolę. W rzeczywistoœci w zależnoœci od wartoœci błędów położenia osi przekładni Nowikowa naprężenia te, jak zostało pokazane w rozdziale 3., mogš wzrosnšć bšdŸ zmaleć.

 

 

5.    WNIOSKI i PODSUMOWANIE

 

Artykuł przedstawia zastosowanie teorii Hertza w obliczeniach wytrzymałoœciowych kół przekładni Nowikowa. Wyznaczono w nim wpływ błędów montażu przekładni na wielkoœć nacisków powierzchniowych. Porównane również zostały maksymalne naprężenia Hertza dla przekładni ewolwentowej oraz Nowikowa.

W przypadku przekładni silnie obcišżonych zazębienie Nowikowa odznacza się teoretycznie większš noœnoœciš na naciski aniżeli zazębienie ewolwentowe. Ponadto błšd rozstawienia osi kół przekładni może korzystnie wpływać na rozkład naprężeń przez przesunięcie punktu styku ku stopie zęba wypukłego, gdzie stosunek œrednich promieni krzywizn jest mniejszy. W zależnoœci od charakteru błędu, przekoszenia osi naprężenia nieznacznie rosnš bšdŸ malejš wzdłuż szerokoœci wieńca, poczšwszy od wejœcia w zazębienie aż do wyjœcia.

 

 

6.  Podziękowania

 

     Badania realizowane w ramach Projektu „Nowoczesne technologie materiałowe stosowane w przemyœle lotniczym” Nr POIG.01.01.02-00-015/08-00 w Programie Operacyjnym Innowacyjna Gospodarka (PO IG). Projekt współfinansowany przez Unię Europejskš ze œrodków Europejskiego Funduszu Rozwoju Regionalnego.

References

 

1.      Dyson A., H.P. Evans, W. Snidle. 1989. “Wildhaber-Novikov circular arc gears: some properties of relevance to their design”. Proceedings of The Royal Society A 425: 341-363.

2.      Johnson K.L. 2003. Contact mechanics. Cambridge: Cambridge University Press.

3.      Markowski T., M. Batsch. 2013. “Analysis of the Contact Region Geometry of the Novikov Convexo-Concave Gears”. In AIRTEC 2013. Frankfurt 5-7.10.2013.

4.      Markowski T., A. Kawalec. 1995. “An Analysis of the Contact Area Parameters Which Influence the Load Capacity of a Mesh”. In 2nd Int. Scientific Colloquium CAE Techniques. Bielefeld 1995.

5.      Markowski T., M. Mijał, E. Rejman. 2000. Podstawy konstrukcji maszyn. Napędy mechaniczne Cz. I. [In Polish: Machine construction basics. Mechanical drives Vol. I]. Rzeszów: Oficyna Wydawnicza Politechniki Rzeszowskiej.

6.      Ochęduszko K. 1985. Koła zębate T.1 Konstrukcja. [In Polish: Gears T.1 Construction]. Warszawa: WNT.

 

 

Received 11.08.2015; accepted in revised form 21.12.2015

 

 

Scientific Journal of Silesian University of Technology. Series Transport is licensed under a Creative Commons Attribution 4.0 International License


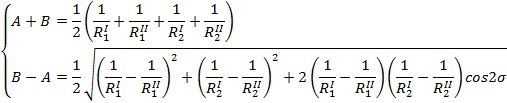
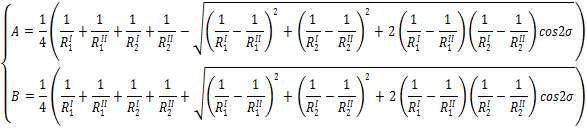
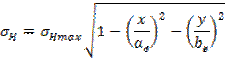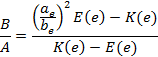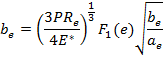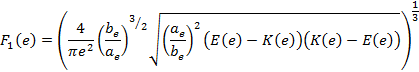[1] Faculty of Mechanical Engineering and Aeronautics, Rzeszow University of Technology, al. Powstańców Warszawy 8, 35-959 Rzeszów, Poland. E-mail: mbatsch@prz.edu.pl.