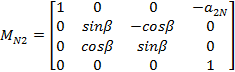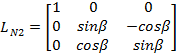Article citation info:

Markowski, T., Batsch, M. Mathematical model of form machining of the convexo-concave Novikov gear teeth. Scientific Journal of Silesian University of Technology. Series Transport. 2016, 90, 137-147. ISSN: 0209-3324. DOI: 10.20858/sjsutst.2016.90.12.

 

 

Tadeusz MARKOWSKI[1], Michał BATSCH[2]

 

 

 

MATHEMATICAL MODEL OF FORM MACHINING OF THE CONVEXO-CONCAVE NOVIKOV GEAR TEETH

 

Summary. Article presents mathematical model of form machining of cylindrical convexo-concave Novikov gear teeth by means of disk-type tools. Example of these king of tools is disk-type milling cutter or grinding wheel. Moreover based on the given convex and concave tooth geometry the tool profile has been established.

Keywords: mathematical model, Novikov convexo-concave gear, machining, disk-type tools

 

 

 

MATEMATYCZNY MODEL OBRÓBKI  KSZTAŁTOWEJ UZĘBIEŃ 

O KOŁOWO-ŁUKOWYM ZARYSIE ZĘBÓW TYPU NOWIKOWA

 

Streszczenie. Artykuł przedstawia model matematyczny kształtowej obróbki uzębień walcowych przekładni zębatych o kołowo-łukowym zarysie zębów typu Nowikowa za pomocą narzędzi krążkowych. Przykładami takich narzędzi mogą być frez krążkowy lub ściernica. Ponadto wyznaczono zarysy narzędzi na podstawie zadanej geometrii kół zębatych o wklęsłym i wypukłym zarysie zębów.

Słowa kluczowe: model matematyczny, przekładnia zębata Nowikova o kołowo-łukowym zarysie zębów, obróbka, frez krążkowy

 

1. WPROWADZENIE

 

     Uzębienie kół przekładni Nowikowa może być wykonywane zarówno metodami kształtowymi, jak i obwiedniowymi [5]. Wśród metod kształtowych wyróżnić można frezowanie frezem trzpieniowym bądź krążkowym. Do metod obwiedniowych zaliczyć można frezowanie frezem ślimakowym, dłutowanie metodami Maaga oraz Fellowsa. Metody kształtowe są znacznie droższe i bardziej czasochłonne w porównaniu do metod obwiednio-wych, dlatego też nie nadają się do produkcji masowej. Ich zaletą jednak jest możliwość wykonywania uzębienia na maszynach niededykowanych do obróbki kół zębatych np. na fre-zarkach. W tym przypadku frezarka musi mieć skrętny wrzeciennik oraz możliwość sprzężenia ruchu posuwowego stołu z ruchem obrotowym koła obrabianego. Takie wyma-gania spełniają 5-osiowe frezarki bądź centra frezarskie ze skrętnym wrzeciennikiem i z osią obrotową. Ponadto obróbka wykańczająca często odbywa się metodą kształtową [2, 4].
W tym przypadku zarys ściernicy ukształtowany jest tak, aby w wyniku sprzężenia jej ruchu
z ruchem półwyrobu można było uzyskać pożądany zarys zębów.

     W artykule przedstawiono kinematykę obróbki kół przekładni Nowikowa narzędziem krążkowym. Wyznaczono również sprzężony z kołem obrabianym zarys narzędzia do obróbki uzębienia wypukłego oraz wklęsłego z wykorzystaniem metody analitycznej [1, 2].

 

 

2. Zarys narzędzia do obróbki uzębienia wypukłego

 

     Rysunek 1 przedstawia matematyczny model przekładni technologicznej, na którą składa się narzędzie oraz obrabiany zębnik o zębach wypukłych.

Wprowadzono trzy układy współrzędnych: xS1, yS1, zS1 związany z obrabianym zębnikiem, pomocniczy xN, yN, zN oraz xNo, yNo, zNo związany z narzędziem. Narzędzie krążkowe o promieniu rN obrabia zębnik o średnicy stóp rf1. Powierzchnie boczne sąsiadujących zębów są obrabiane jednocześnie w wyniku sprzężenia ruchów obrotowego i posuwowego koła.

     Prędkości kątowa oraz liniowa obrabianego koła powinny być powiązane ze sobą zależnością (1)

 

(1)

 

     Odległość pomiędzy osiami obrotu narzędzia oraz zębnika wyraża się wzorem (2)

 

(2)

 

     Powierzchnia zęba zębnika w układzie S1 reprezentowana jest przez wektor (3) oraz wersor normalny (4):

 

(3)

(4)

 

 

gdzie:

αw – czołowy kąt przyporu,

r1 – promień podziałowy zębnika,

ρ1 – promień zarysu zęba wypukłego,

dCO’ – odległość pomiędzy centralnym punktem zazębienia C a środkiem zarysu zęba wypukłego O’,

β – kąt pochylenia linii zęba na średnicy podziałowej, φ1,

θ1 – parametry powierzchni,

φSYM1 – kąt zapewniający, że oś xS1 będzie osią symetrii zarysu wrębu międzyzębnego w przekroju czołowym zaznaczonym na rysunku 1.

 

 

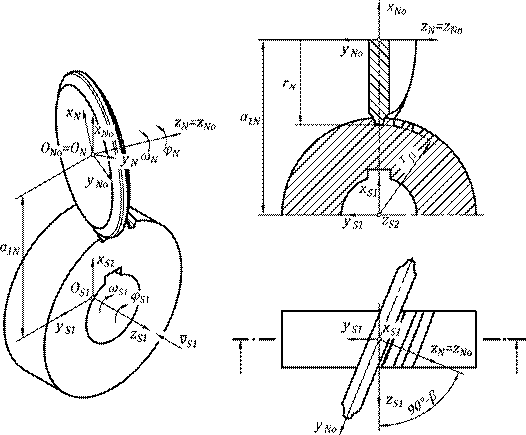
Rys. 1. Obróbka uzębienia zębnika narzędziem krążkowym

 

 

 

 

Powierzchnia zęba zębnika w układzie współrzędnych narzędzia xNo, yNo, zNo wyraża się zależnością (5)

 

,

(5)

 

gdzie:

MNoN – jednorodna macierz transformacji z układu N do No,

MN1 – jednorodna macierz transformacji z układu 1 do N.

 

     Powyższe macierze dane są zależnościami (6) oraz (7):

 

(6)

 

(7)

 

     Podobnie wersor normalny do powierzchni zęba zębnika w układzie współrzędnych narzędzia xNo, yNo, zNo wyraża się zależnością (8):

 

,

(8)

 

gdzie:

LNoN – macierz transformacji z układu N do No,

LN1 – macierz transformacji z układu 1 do N.

 

     Macierze te dane są wzorami (9) i (10):

 

(9)

 

(10)

 

     Kierunek prędkości dowolnego punku powierzchni narzędzia określony jest przez wektor (11):

 

(11)

 

 

     Musi być on styczny do powierzchni bocznej obrabianego zęba. Styczność ta wystąpi, gdy kąt pomiędzy nim a wersorem normalnym do powierzchni zęba zębnika będzie kątem prostym, a więc gdy spełnione zostanie równanie (12):

 

(12)

 

     Rozwiązanie tego równania dla kolejnych dyskretnych wartości kąta obrotu narzędzia  oraz dla kolejnych dyskretnych wartości parametru powierzchni bocznej zęba zębnika  pozwala na wyznaczenie parametrycznej reprezentacji powierzchni bocznej narzędzia w postaci (13):

 

(13)

 

     Rysunek 2 przedstawia wygenerowaną powierzchnię boczną narzędzia do obróbki uzębienia zębnika w układzie współrzędnych No.

 

 

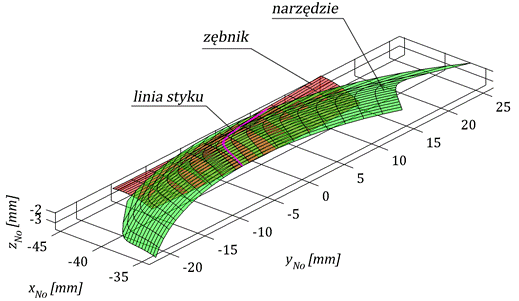
Rys. 2. Powierzchnia narzędzia do obróbki uzębienia wypukłego, powierzchnia boczna zęba zębnika oraz ich linia styku w układzie współrzędnych koła obrabianego

 

     Zarys narzędzia krążkowego jest uzyskiwany w wyniku przekroju powierzchni narzędzia płaszczyzną xNozNo, a zatem jest on zbiorem punktów powierzchni narzędzia, dla których współrzędna yNo przyjmuje wartość zero. Zarys ten dla narzędzia do obróbki uzębienia wypukłego zębnika pokazano na rys. 3.

 

 

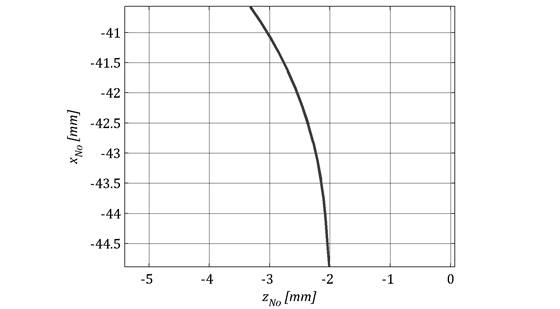
Rys. 3. Zarys narzędzia do obróbki wypukłego uzębienia zębnika

 

 

3. zarys narzędzia do obróbki uzębienia wklęsłEgo

 

     Rysunek 4 przedstawia model przekładni technologicznej, na którą składa się narzędzie oraz obrabiane koło.

 

 

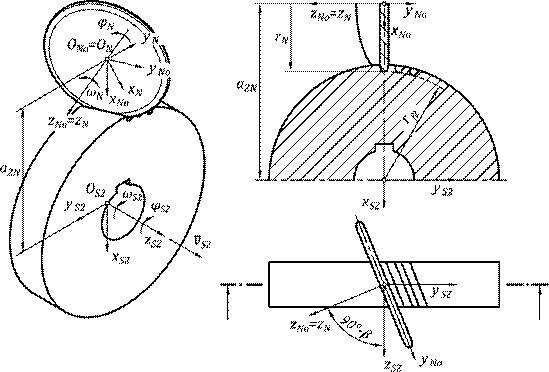
Rys. 4. Obróbka uzębienia koła narzędziem krążkowym

 

Tak samo jak w przypadku wyznaczania zarysu narzędzia do obróbki uzębienia wklęsłego wprowadzono trzy układy współrzędnych: xS2, yS2, zS2 związany z obrabianym kołem, pomocniczy xN, yN, zN oraz xNo, yNo, zNo związany z narzędziem. Narzędzie krążkowe o promieniu rN obrabia koło o średnicy stóp rf2. Powierzchnie boczne sąsiadujących zębów są obrabiane jednocześnie w wyniku sprzężenia ruchów obrotowego i posuwowego koła. Prędkości kątowa oraz liniowa obrabianego koła powinny być powiązane ze sobą zależnością (14):

 

(14)

 

Odległość pomiędzy osiami obrotu narzędzia oraz koła wyraża się wzorem (15):

 

(15)

 

     Powierzchnia zęba koła w układzie S2 reprezentowana jest przez wektor (16) oraz wersor normalny (17):

 

(16)

 

,

(17)

 

gdzie:

αw – czołowy kąt przyporu,

r2 – promień podziałowy koła,

ρ2 – promień zarysu zęba wklęsłego,

dCO’ – odległość pomiędzy centralnym punktem zazębienia C a środkiem zarysu zęba wypukłego O’,

β – kąt pochylenia linii zęba na średnicy podziałowej, φ2,

θ2 – parametry powierzchni,

φSYM2 – kąt zapewniający, że oś xS2 będzie osią symetrii zarysu wrębu międzyzębnego w przekroju czołowym zaznaczonym na rys. 4.

 

 

 

 

 

     Powierzchnia zęba koła w układzie współrzędnych narzędzia xNo, yNo, zNo wyraża się zależnością (18):

 

,

(18)

 

gdzie:

MNoN – jednorodna macierz transformacji z układu N do No,

MN2 – jednorodna macierz transformacji z układu 2 do N.

 

     Powyższe macierze dane są zależnościami (19) oraz (20):

 

(19)

 

(20)

 

     Podobnie wersor normalny do powierzchni zęba koła w układzie współrzędnych narzędzia xNo, yNo, zNo wyraża się zależnością (21):

 

,

(21)

 

gdzie:

LNoN – macierz transformacji z układu N do No,

LN2 – macierz transformacji z układu 2 do N.

 

     Macierze te dane są wzorami (22) i (23):

 

(22)

 

(23)

 

     Kierunek prędkości dowolnego punku powierzchni narzędzia określony jest przez wektor (24):

 

(24)

 

 

     Musi być on styczny do powierzchni bocznej obrabianego zęba. Styczność ta wystąpi, gdy kąt pomiędzy nim a wersorem normalnym do powierzchni zęba koła będzie kątem prostym, a więc gdy spełnione zostanie równanie (25):

 

(25)

 

     Rozwiązanie tego równania dla kolejnych dyskretnych wartości kąta obrotu narzędzia  oraz dla kolejnych dyskretnych wartości parametru powierzchni bocznej zęba koła  pozwala na wyznaczenie parametrycznej reprezentacji powierzchni bocznej narzędzia w postaci (26):

 

(26)

 

     Rysunek 5 przedstawia wygenerowaną powierzchnię boczną narzędzia do obróbki uzębienia koła w układzie współrzędnych No.

 

 

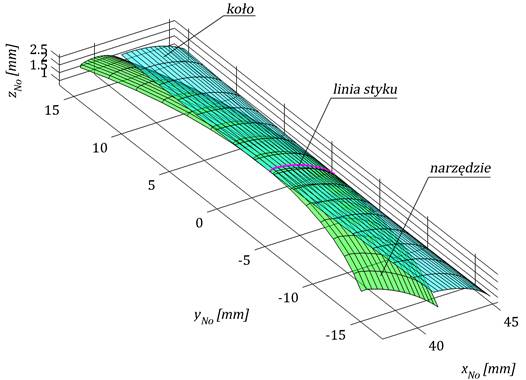
Rys. 5. Powierzchnia narzędzia koła, powierzchnia boczna koła oraz ich linia styku w układzie współrzędnych koła obrabianego

 

     Podobnie jak w przypadku z rozdziału 2 jego zarys uzyskiwany jest w wyniku przekroju powierzchni narzędzia płaszczyzną xNozNo. Zarys ten dla narzędzia do obróbki uzębienia wklęsłego koła przedstawiono na rys. 6.

 

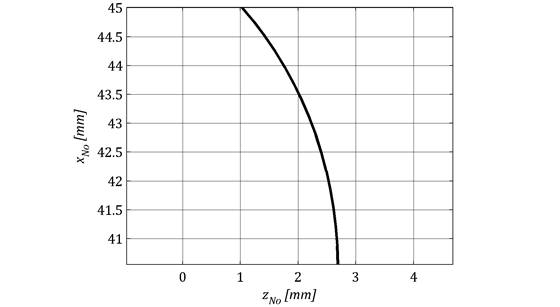
Rys. 6. Zarys narzędzia do obróbki wklęsłego uzębienia koła

 

 

4. WNIOSKI i PODSUMOWANIE

 

Przedstawiony matematyczny model kształtowej obróbki uzębień może być wykorzystany podczas projektowania narzędzi krążkowych. W zależności od przyjętych parametrycznych równań powierzchni bocznej obrabianego zęba, które definiują jego geometrie, może on posłużyć do symulacji obróbki uzębień walcowych dowolnego typu. Tego rodzaju obróbka daje możliwość wykonywania uzębienia na maszynach niededykowanych do obróbki kół zębatych, co jest zaletą w przypadku produkcji jednostkowej.

Narzędzia krążkowe do obróbki uzębień Nowikowa mają zarys, który z dużą dokładnością można przybliżyć łukiem okręgu. W omawianych w rozdziałach 2 i 3 metodach wyznaczania zarysu narzędzi zakładano jednoczesną obróbkę dwóch sąsiadujących powierzchni bocznych zębów. W praktyce, aby móc kontrolować wielkość luzu międzyzębnego, a co za tym idzie szerokość wrębu międzyzębnego, narzędzia mogą być wykonane o nieco mniejszej szerokości niż wynika to z przeprowadzonych obliczeń. Zmiana szerokości może polegać na nieznacznym przesunięciu środka łuku okręgu stanowiącego zarys narzędzia. Ponadto przesunięcie to umożliwia obróbkę uzębienia ze zmianą kąta pochylenia linii zęba. Wówczas możliwe jest wprowadzanie modyfikacji w postaci fazowania bądź beczułkowania, o ile skręt wrzeciennika obrabiarki może być sterowany numerycznie.

 

 

5. Podziękowania

 

     Badania realizowane w ramach Projektu „Nowoczesne technologie materiałowe stosowane w przemyśle lotniczym”, Nr POIG.01.01.02-00-015/08-00 w Programie Operacyjnym Innowacyjna Gospodarka (PO IG). Projekt współfinansowany przez Unię Europejską ze środków Europejskiego Funduszu Rozwoju Regionalnego.

References

 

1.      Litvin F.L., A. Fuentes A. 2004. Gear Geometry and Applied Theory. Cambridge: Cambridge University Press.

2.      Markov V.M., A.S. Kosterin. 2008. „Simulation of the Working Surface of a Grinding Wheel in Complex Gear Cutting”. Russian Engineering Research 28: 1125-1128.

3.      Radzewich S.P. 2010. Gear Cutting Tools. Fundamentals of Design and Computation. Abingdon: CRC Press.

4.      Shih Y.P, S.D. Chen S.D. 2012. “A flank correction methodology for a five-axis CNC gear profile grinding machine”. Mechanism and Machine Theory 47: 31-45.

5.      Watson H.J. 1970. Modern Gear Production. Bradley: Pergamon Press.

 

 

Received 17.09.2015; accepted in revised form 30.12.2015

 

 

Scientific Journal of Silesian University of Technology. Series Transport is licensed under a Creative Commons Attribution 4.0 International License


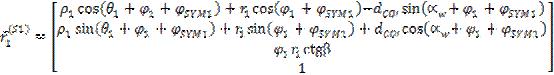
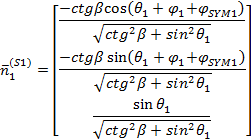
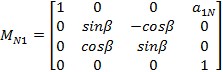
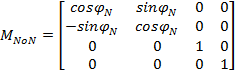
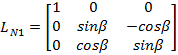
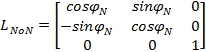
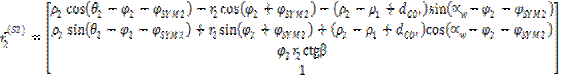
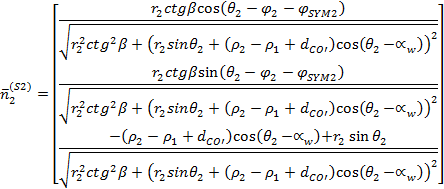[1] Faculty of Mechanical Engineering and Aeronautics, Rzeszow University of Technology, al. Powstańców Warszawy 8, 35-959 Rzeszów, Poland. E-mail: tmarkow@prz.edu.pl.

[2] Faculty of Mechanical Engineering and Aeronautics, Rzeszow University of Technology, al. Powstańców Warszawy 8, 35-959 Rzeszów, Poland. E-mail: mbatsch@prz.edu.pl.