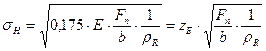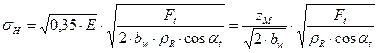Article citation info:

Vojtková, J. Reduction of contact stresses using involute gears with asymmetric teeth. Scientific Journal of Silesian University of Technology. Series Transport. 2015, 89, 179-185. ISSN: 0209-3324. DOI: 10.20858/sjsutst.2015.89.19.

Jarmila VOJTKOVÁ[1]

REDUCTION OF CONTACT STRESSES USING INVOLUTE GEARS WITH ASYMMETRIC TEETH

Summary. Asymmetrical involute gears have a different value of the operating pressure angle for right and left side of the gear. These teeth are suitable for one direction of rotation. Such teeth enable to change the length of the generating line. They enable to improve the value of reduced radii of curvature. Asymmetrical teeth allow reducing the values of Hertz's pressures, especially on the root of the teeth. Hertz pressures are directly related to the asymmetry.

Keywords: contact stresses, gear, involute, asymmetric teeth

1. Introduction

In practice, cogwheels with involute gears are used the most. Their production is common and their accuracy is aceptable. [1-7]. However, to lower the value of contact stresses, gears with asymmetric teeth might be more suitable. Their price should not be a main criterion when working with them. With a well-designed gear with asymmetrical teeth, a considerable decrease in the values of contact stresses can be noticed, and in some cases also a decrease in vibrations. From this point of view, the spur gears with non-symmetrical teeth are becoming a great alternative. [1-2].

2. Suitable TOOTH Design Area For GEAR with asymmetric teeth

The driving side has a differnet pressure angle than the opposite side, and therefore an asymetrical tooth is being created. An angle larger than 20° is more advantageous for the driving side. The angle of the opposite side has a considerable influence only during the reverse movement. Base circle diameter significantly decreases with increasing pressure angle. The larger the difference between the angles of a profile, the more pronounced is the asymmetry, and hence there is a significant difference between the diameters of the base circle. [1].

An asymmetrical tooth, an axis of tooth, and a pitch circle are drawn on Fig. 1. The circular pitch measured on the pitch circle is identical for the left and right side. The tooth thickness, measured mostly on a top land, is changing relative to the angle of stress, which influences the ability to create a correct tooth.

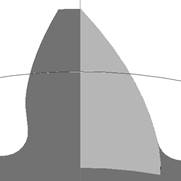
Fig. 1. Asymmetrical tooth, h_a^*= 1, left side pressure angle α_L=20º, right side pressure angle α_P=35º

The minimum number of teeth with allowable undercutting z´_min

(1)

Where:

h_a^* − sufficient tooth addendum,

α − pressure angle [°].

Values of a minimal amount of teeth z´_min relative to the angle of profile α, for various values of top land tooth height h_a^*, are depicted on Fig. 2. The curves take into consideration the allowable undercutting. For larger values of the profile α angle, the values of minimal amount of teeth are decreasing pronouncely.

The area of the accurate tooth design is dependent on the following parameters:

• number of teeth,
• sufficient tooth addendum h_a^*,
• pressure angle for the opposite side of tooth,
• the stresses on the non-funtional side of the tooth,
• the required value of top land tooth thickness.

^Z´min

α (°)

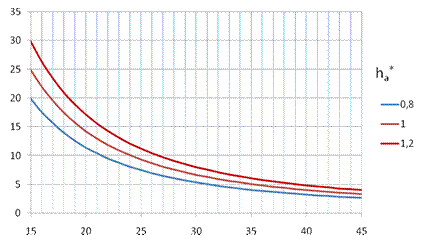
Fig. 2. The minimum number of teeth with allowable undercut depending
on the pressure angle

Half the top land thickness

(2)

Where:

d_a − tip circle diameter [mm],

d − pitch circle diameter [mm],

m – module [mm],

α_a − pressure angle at the tip circle [°].

These parameters imply a possible design area of an accurate tooth creation, which satisfies the geometrical parameters. An area for accurate tooth creation for parameters z₁=17, h_a^*=1 is shown in Fig. 3. For a certain number of teeth, based on an angle α_L, the values of the angle on the right side can be determined in the graph (Fig. 3). For example, z₁=17, h_a^*=1, α_L=20° can have an angle α_P in the interval < 20°, 38.5°>_. This area decreases in size with a smaller number of teeth.

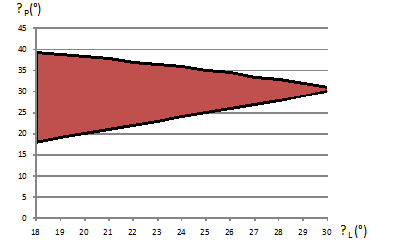
Fig. 3. Suitable tooth design area for z₁=17, h_a^*=1

Table 1

The top land thickness and contact ratio for m=10mm, gear ratio u=1

ha^*	z1	αL (°)	αP (°)	saL/2 (mm)	saP/2 (mm)	εαL	εαP	z2hL
0,9	8	25	38	2,692	-0,185	1,128	1,041	11
	10	23	40	3,190	-0,550	1,202	1,059	22
	14	19	43,5	4,013	-1,362	1,370	1,083	27
	17	17	45,5	4,401	-1,898	1,488	1,097	30
1	10	24	32,5	2,232	0,372	1,294	1,194	18
	14	20	37,5	3,230	-0,669	1,463	1,201	26
	17	18	39,5	3,697	-1,116	1,582	1,209	31
1,1	14	21	30	2,375	0,270	1,553	1,370	25
	17	19	33,5	2,929	-0,351	1,672	1,361	32

The limits values of the angles α for the right and left side, with a full degree precision for the left side and 0,5° precision for the right side, for a various amount of teeth are mentioned in Tab. 1. The values of half top land tooth thickness are also mentioned there. The value z_2hL is the limit value of the number of teeth, for the gear ratio u=1. If the number of teeth is greater than z_2hL, point A is outside the interval N₁N₂ (interference). For a larger gear ratio, the value of the limit of the teeth z_2h increases.

3. The radii of curvature and Hertz pressures

A view of various sides of the tooth, where the length of the contact line and radii are changing, is on Fig. 4.The change of pressure angle α leads to changes in the radii of curvature (Fig. 4), which affect the Hertz pressures. Tab. 2 shows the values of the radii of curvature, mesh points A, C. [1].

a) b)

Fig. 4. Mesh assymetrical toth: a) driving side α_L=20°, b) driving side α_P=35°

The value of Hertz pressure is changing in relation to the contact point. It has the least advantageous values in the place of the first mesh point, at the dedendum of the pinion. The regular values of the pressure in the gearing can be approximately determined in a following matter: For symmetrical gearing, if the pressure value of 100% is at the pitch point, then this value at the dedendum is approximately 150% and approximately 95% at the top of the pinion in relation to the gearing geometry. [8]. The values of the pressures can be determined based on the circumference force. The second option is to determine these values on the basis of normal force, which value changes depending only on the amount of tooth pairs in the mesh, and is constant for a single contact. Double tooth contact is also being considered in the calculation.

Table 2

Reduced radii of curvature and values corresponding to Hertz pressure for F_t=1N

z1	z2	α (°)	Point C			Point A
			ρ1C (mm)	√(Ft/(ρR.cosαt)) (N/mm)^-1/2	%	ρ1A (mm)	√(Ft/(ρR.cosαt)) (N/mm)^-1/2	%
10	10	24	20,337	0,3281	100	1,769	0,5688	173
		32,5	26,865	0,2971	91	11,048	0,2497	79
	18	24	20,337	0,2894	100	0,022	4,9947	1726
		32,5	26,865	0,2620	91	10,119	0,2602	90
14	14	20	23,941	0,2982	100	2,351	0,4879	164
		37,5	42,613	0,2432	82	27,643	0,1837	62
	26	20	23,941	0,2615	100	0,016	5,7701	2207
		37,5	42,613	0,2133	82	27,079	0,1730	66
17	17	18	26,266	0,2830	100	2,634	0,4584	162
		39,5	54,067	0,2190	77	39,408	0,1608	57
	31	18	26,266	0,2490	100	0,041	3,5680	1433
		39,5	54,067	0,1927	77	38,991	0,1494	60

Reduced radius of curvature ρ_R for the mesh points:

(3)

_Where:

_{ρ1 – radius of curvature with respect to the pinion [mm],}

_{ρ2 – radius of curvature with respect to the wheel [mm].}

Hertz pressures are directly related to the asymmetry. The values of the reduced radii of curvature at the pitch point C and point A are calculated in Fig. 2. The value √(F_t/(ρ_R.cosα)) is in proportion to the course of stresses. This value for pitch point C is defined as 100%. The change corresponding to the change in stresses at a specific point can be seen in Fig. 2. For example, for values z₁= z₂=17, h_a^*=1, an angle α_L=18° is the stress at the pitch point C with the value 100%, in point A with 162%, and decreases for angle α_P=39,5° to 77% in point C, and to 57% in point A. If the angle of the driving side is 39,5°, the values of stresses are considerably more advantageous.

ρ₁

[mm]

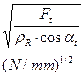
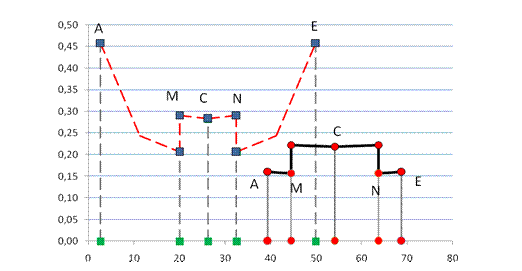
Fig. 5. The course of mathematical term determining the course of a Hertz pressure, force
F_t = 1N, z₁=17, z₂=17, h_a^*=1, α_L=18°, α_P=39,5° with a double tooth contact

_{Hertz pressure by normal force}

(4)

_{Hertz pressure by tangential force}

(5)

_Where:

_{zM − material factor [MPa1/2],}

_{Ft − tangential force [N],}

_{Fn − normal force [N],}

_{bw − axial face width [mm],}

_{αt − pressure angle in a transverse plane [°],}

_{E − modulus of elasticity [MPa].}

4. Conclusion

The use of gears with asymmetric teeth can be a good alternative to reduce Hertz pressures. Well-designed gearing can be achieved to reduce the size, significantly reduce contact stresses especially in the dedendum of the pinion.

This paper was written in the framework of Grant Project VEGA: “1/0688/12– Research and application of universal regulation system in order to master the source of mechanical systems excitation.”

References

1. Vojtková J. 2014. „Effect of asymmetry on radii of curvature for spur gears with nonsymmetrical teeth“. Scientific Journal of Silesian University of Technology. Series Transport 84: 47-51. ISSN 0209-3324.

2. Di Francesco G., S. Marini. 2007. Asymetric Teeth: Bending Stress Calculation. In:
http:// www.geartechnology.com. March/April 2007.

3. Wojnar G., P. Czech, P. Folega. 2014. “Problem with Diagnosing local faults of gearboxes on the basic of vibration signal”. Transaction of the Universities of Košice 2: 95-100. ISSN: 1335-2334.

4. Czech P., P. Folega P., G. Wojnar. 2014. „Taking Advantage of empirical mode decomposition in diagnostig IC engine faults”. Transaction of the Universities of Košice 2: 17-22. ISSN: 1335-2334.

5. Czech P., J. Mikulski. 2014. “Application of Bayes classifier and entropy of vibration signals to diagnose damage of head gasket in internal combustion engine of a car”. Communications in Computer and Information Science 471: 225-232. ISSN: 1865-0929.

6. Homišin J., P. Kaššay, P. Čopan. 2014. „Possibility of torsional vibration extremal control”. Diagnostyka 15(2): 7-12.

7. Haľko J., S. Pavlenko. 2012. „Analytical suggestion of stress analysis on fatigue in contact of the cycloidal - vascular gearing system“. Scientific Journal of Silesian University of Technology. Series Transport 76: 63-66. ISSN 0209-3324.

8. Moravec V. 2001. Konstrukce strojů a zařízení II. Montanex. [In Slovak: Construction machinery and equipment II].

Received 09.05.2015; accepted in revised form 24.09.2015

Scientific Journal of Silesian University of Technology. Series Transport is licensed under a Creative Commons Attribution 4.0 International License

---

[1] Faculty of Mechanical Engineering, The Technical University of Košice, Letná 9 Street, 042 00 Košice, Slovak Republic. E-mail: jarmila.vojtkova@tuke.sk