Article citation info:

Połowniak, P. Chosen aspects of modeling globoid worm in CATIA system. Scientific Journal of Silesian University of Technology. Series Transport. 2015, 89, 127-137. 

ISSN: 0209-3324. DOI: 10.20858/sjsutst.2015.89.14.

Piotr POŁOWNIAK[1]

CHOSEN ASPECTS OF MODELING GLOBOID WORM IN CATIA SYSTEM

Summary. The paper presents methods of modelling the globoid worm with rectilinear profile using CATIA system. The methods of modelling of globoid surface, among others throw extending a profile accross the screw lines of globoid (Sweep), by making the surface as multi section (Multi Section Surface) are specified. Some steps by modelling the globoid surface are automated by writing macros in the CATIA system. The accuracy of the models of globoid worms obtained by different methods is presented. The capabilities of the CATIA system by modelling are presented.

Keywords: model, globoid worm, CATIA system

WYBRANE ASPEKTY MODELOWANIA ŚLIMAKA GLOBOIDALNEGO W ŚRODOWISKU CATIA

Streszczenie. W artykule przedstawiono sposoby modelowania ślimaka globoidalnego o zarysie prostoliniowym z wykorzystaniem systemu CATIA. Wyróżniono metody modelowania powierzchni globoidalnej m.in. przez przeciągnięcie odcinka po liniach śrubowych globoidalnych (Sweep), przez wykonanie powierzchni jako wieloprzekrojowej (Multi-Section Surface). Pewne etapy tworzenia powierzchni zostały zautomatyzowane przez napisanie makr w systemie CATIA. Omówiono dokładność modeli ślimaków globoidalnych otrzymanych różnymi metodami. Omówiono możliwości systemu przy modelowaniu.

Słowa kluczowe: model, ślimak globoidalny, system CATIA

1. WPROWADZENIE

W przekładni ślimakowej globoidalnej zęby ślimaka nacięte są na wklęsłej powierzchni obrotowej, w której promień podziałowy ślimaka jest równy promieniowi podziałowemu współpracującej ślimacznicy [1].

Poprawnie geometrycznie zamodelowany ślimak może zostać wykorzystany w celu wygenerowania ślimacznicy w środowisku CAD, a następnie do analiz śladu styku i współpracy metodą CAD [2]. Modele mogą również posłużyć do analiz z wykorzystaniem metody elementów skończonych.

Zasada modelowania ślimaka globoidalnego została przedstawiona przez Autorów [1]. W poniższym artykule zaprezentowano wybrane aspekty modelowania ślimaka globoidalnego z określeniem dokładności otrzymanego modelu przy wykorzystaniu danych metod modelowania w systemie CATIA V5 R21.

2. MODELOWANIE ŚLIMAKA GLOBOIDALNEGO – WYBRANE ASPEKTY

Na rys. 1 przedstawiono podstawowe parametry przekładni ślimakowej globoidalnej, które należy określić w celu wykonania modelu ślimaka globoidalnego. Są to: liczba zębów ślimaka i ślimacznicy, moduł zęba, odległość osi przekładni, kąt zarysu zęba, średnica podziałowa ślimaka, średnica podziałowa ślimacznicy.

W ślimakach globoidalnych zarys zębów w przekroju osiowym jest prostoliniowy. Ślimak globoidalny ma stałą podziałkę kątową mierzoną względem środka ślimacznicy.

Ogólny tok postępowania przy modelowaniu ślimaka globoidalnego został przedstawiony w artykule [1]. Zostało wyznaczone równanie globoidalnej linii śrubowej, które jest podstawą do poprawnego zamodelowania powierzchni globoidalnej. Do generowania punktów globoidalnej linii śrubowej stworzono algorytm w programie Matlab R2013a. Otrzymane zbiory punktów linii śrubowej wyeksportowano do systemu CATIA V5 R21, w którym stworzono model.

Na odpowiednich zbiorach punktów rozpięto splajny przybliżające globoidalne linie śrubowe (rys. 2).

Przy wyciągnięciu zarysu ślimaka po jednej ścieżce − linii globoidalnej nie są uwzględnione zmiany krzywizn powierzchni, co widać na rys. 3.

Stworzone powierzchnie nie pokrywają się z globoidalnymi liniami śrubowymi, które są granicami dla tych powierzchni. Model z rys. 3 jest niepoprawny.

Aby były uwzględnione zmiany krzywizn powierzchni, należy przeciągnięcie profilu realizować po dwóch ścieżkach. Każdą powierzchnię: boczną, wierzchołkową i podstaw wykonuje się w oddzielnych operacjach (Sweep − Explicit) (rys. 4).

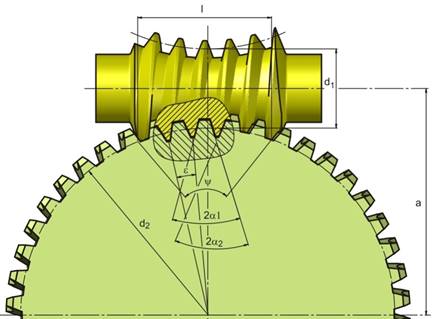
Rys. 1. Przekładnia ślimakowa globoidalna, wybrane parametry geometryczne: a − odległość osi ślimaka i ślimacznicy, d₁ − średnica podziałowa środkowego przekroju ślimaka,
d₂ − średnica podziałowa ślimacznicy, ε − kąt środkowy odpowiadający podziałce,
α₁ − kąt zarysu zębów ślimaka, α₂ − kąt zarysu zębów ślimacznicy, l − czynna długość ślimaka, ψ − kąt opasania

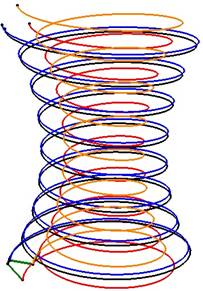
Rys. 2. Globoidalne linie śrubowe

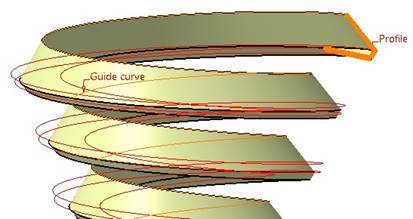
Rys. 3. Wyciągnięcie zarysu ślimaka po jednej ścieżce; fragment modelu z liniami śrubowymi globoidalnymi (Guide curve – ścieżka, Profile – profil)

a)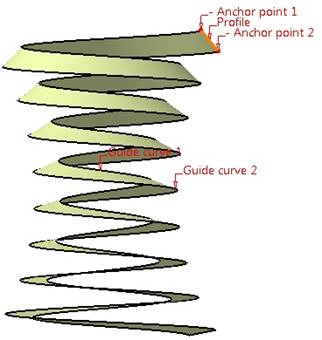b)

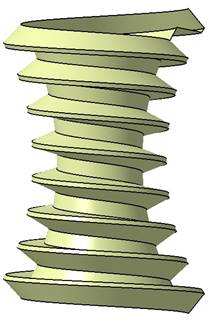
Rys. 4. Tworzenie powierzchni globoidalnej przez wyciąganie profilu po ścieżkach; a) powierzchnia jednego boku, b) wszystkie powierzchnie ślimaka globoidalnego (Guide curve – ścieżka, Profile – profil, Anchor point – punkt bazowy, Sweep profile plane – płaszczyzna profilu przyjętego do wyciągnięcia przez system CAD, Sweep start plane – płaszczyzna profilu zadanego do wyciągnięcia, Sweep end plane – płaszczyzna końcowa wyciągnięcia)

Możliwe jest też wykonanie powierzchni globoidalnej przez wyciągnięcie powierzchni między dwoma ścieżkami (Sweep – Line) (rys. 5).

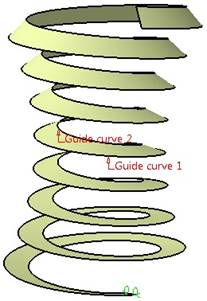
Rys. 5. Tworzenie powierzchni globoidalnej przez wyciągnięcie powierzchni
między ścieżkami (Guide curve – ścieżka)

Kolejną metodą jest wykonanie powierzchni jako wieloprzekrojowej. Utworzono wiele odcinków pomiędzy odpowiednimi punktami linii śrubowych globoidalnych, będących przekrojami osiowymi zarysu (rys. 6).

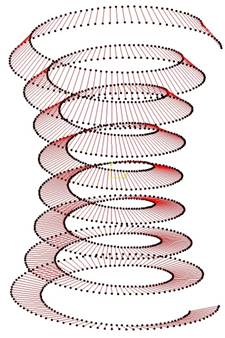
Rys. 6. Tworzenie odcinków pomiędzy odpowiednimi punktami linii śrubowych globoidalnych dla jednego boku ślimaka

Metoda ta jest bardziej pracochłonna. Dlatego w systemie CATIA V5R21 stworzono makro, które łączy odpowiednie punkty linii śrubowych globoidalnych w odcinki dla jednego i drugiego boku ślimaka. Powierzchnię wieloprzekrojową wykonano z wykorzystaniem funkcji Multi Section Surface. Powierzchnię rozpięto na odcinkach (rys. 7).

Ponieważ nie można wybrać profili - odcinków zbiorczo, należy po kolei je wskazywać, więc stworzono makro, które dla polecenia Multi Section Surface wybiera automatycznie wszystkie odcinki tworzące powierzchnię wieloprzekrojową. Powierzchnię wierzchołkową i podstawę zęba modelowano przez wyciągnięcie profilu po ścieżkach (rys. 7).

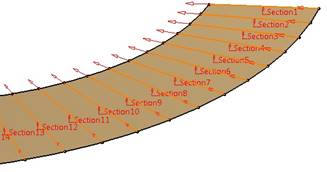
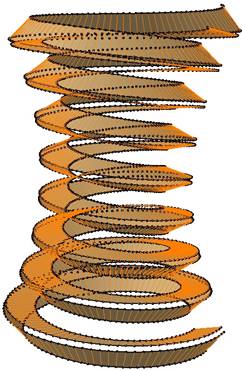
Rys. 7. Powierzchnia globoidalna wykonana metodą wieloprzekrojową Multi Section Surface: a) fragment boku z zaznaczonymi profilami powierzchni, b) boki ślimaka

W poleceniu Multi Section Surface po wskazaniu profili i ścieżek – prowadnic, program generował błąd. Błąd ten jest związany z obszarami kwadrantowymi wzdłuż linii śrubowych co obrót 2π (rys. 8). Podobny błąd system generował dla jednej prowadnicy (Guide).

Dlatego wybrano polecenie Spine (kręgosłup) dla funkcji Multi-Section Surface. Program stworzył powierzchnię (rys. 9).

Chcąc stworzyć powierzchnię wieloprzekrojową z prowadnicami, należy podzielić linie śrubowe globoidalne. Podział następuje w obszarach kwadrantowych (co jeden obrót).

Powierzchnie wieloprzekrojowe z wyborem profili i prowadnic pokazano na rys. 11. Powierzchnie te należy połączyć poleceniem Joint.

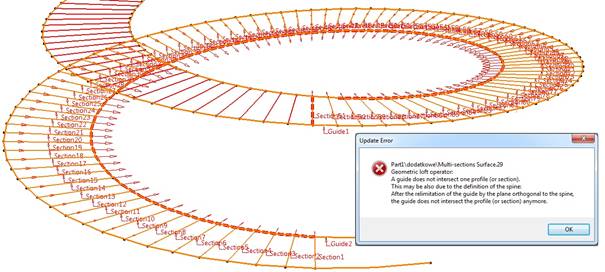
Rys. 8. Polecenie Multi Section Surface z wyborem profili i prowadnic

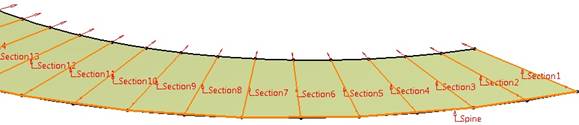
Rys. 9.  Polecenie Multi Section Surface z wyborem profili i kręgosłupa

Rys. 10. Podział linii śrubowych globoidalnych

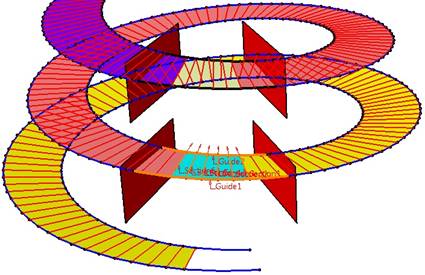
Rys. 11. Powierzchnie wieloprzekrojowe stworzone poleceniem Multi Section Surface z wyborem profili i prowadnic

Przedstawionymi metodami wykonano powierzchnie globoidalne ślimaka. Natomiast metodą wieloprzekrojową Multi Section Surface (rys. 12) i metodą przeciągania Sweep wykonano przekrój osiowy dla ślimaka globoidalnego.

Rys. 12. Ślimak globoidalny stworzony metodą wieloprzekrojową Multi-Section Surface z wyborem profili i prowadnic; wyodrębniono przekrój osiowy ślimaka

Ślimak globoidalny wykonany metodą wieloprzekrojową ma przekrój osiowy prostoliniowy, co jest poprawne. W przypadku gdy powierzchnia boku zęba modelowana jest przez przeciągnięcie odcinka po dwu ścieżkach – liniach śrubowych globoidalnych lub rozwinięta jest pomiędzy ścieżkami, dochodzi do niewielkiego zniekształcenia powierzchni. Jest to wynikiem tego, iż profil wyjściowy (odcinek) znajdujący się w płaszczyźnie Sweep start plane (płaszczyźnie profilu zadanego do wyciągnięcia równoważną z płaszczyzną osiową modelowanego ślimaka) jest sprowadzany do płaszczyzny normalnej do jednej ze ścieżek (do płaszczyzny Sweep profile plane) (rys. 13). Tym samym utworzona powierzchnia w przekroju osiowym ślimaka nie jest prostoliniowa.

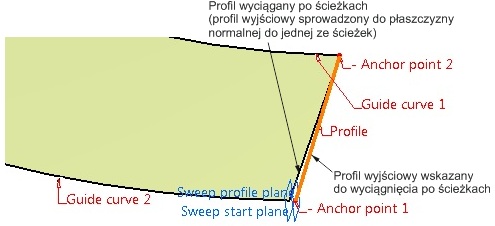
Rys. 13. Przyczyna błędu przy wyciąganiu po ścieżkach (początkowy fragment powierzchni śrubowej globoidalnej) (Guide curve – ścieżka, Profile – profil, Anchor point – punkt bazowy, Sweep profile plane – płaszczyzna profilu przyjętego do wyciągnięcia przez system CAD, Sweep start plane – płaszczyzna profilu zadanego do wyciągnięcia)

Następnie przedstawiono porównanie metod wykonania powierzchni. Do tego celu wykorzystano funkcję systemu CATIA Deviation Analysis, w której wskazuje się powierzchnie referencyjne oraz mierzone. Za odniesienie przyjęto powierzchnie wykonane poleceniem Multi Section Surface tylko ze wskazaniem profili. Na rys. 14 pokazano przykładową analizę porównawczą powierzchni wykonanych metodą Multi Section Surface ze wskazaniem profili oraz ze wskazaniem profili i kręgosłupa.

Poniżej przedstawiono porównanie powierzchni w formie tabelarycznej dla danych metod modelowania. Za odniesienie przyjęto metodę Multi-Section Surface ze wskazaniem tylko profili.

Tablica 1 Porównanie powierzchni ślimaka globoidalnego wykonanych różnymi metodami
	Metoda odniesienia − Multisection Surface ze wskazaniem profili
Metoda porównywana	Odchylenie [mm]
Multisection Surface ze wskazaniem profili i kregosłupa	-0,006÷0,008
Połączenie wielu powierzchni Multisection Surface po podziale linii śrubowej globoidalnej	-0,006÷0,006
Powierzchnia stworzona przez wyciągnięcie profilu po ścieżkach (Sweep - Explicit)	-0,01÷0,004
Powierzchnia stworzona jako wyciągnięcie między ścieżkami (Sweep - Line)	-0,01÷0,004

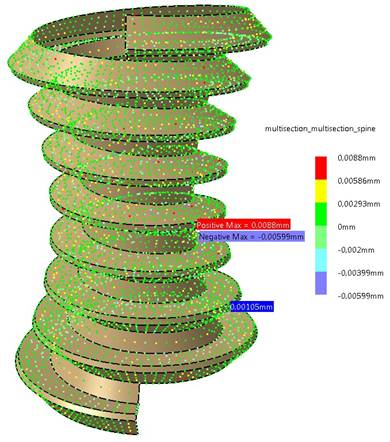
Rys. 14. Porównanie powierzchni utworzonych dwiema metodami – Multisection Surface ze wskazaniem profili, Multisection Surface ze wskazaniem profili i kręgosłupa

3. WNIOSKI

Przedstawione metody powierzchniowe modelowania ślimaka globoidalnego wykorzystują zaawansowane narzędzia systemu CATIA. Linie śrubowe globoidalne wyznaczone analitycznie są podstawą modelowania. Wyróżniono kilka metod modelowania boku zęba. Za najdokładniejsze przyjmuje się te z wykorzystaniem polecenia Multi-Section Surface. Otrzymuje się wówczas prostoliniowy zarys zęba. Dla tej metody wyróżniono kilka opcji. Za najbardziej pracochłonną uznaje się tę z podziałem linii śrubowej na części i tworzenie poszczególnych powierzchni, a następnie ich połączenie. Tworzenie powierzchni metodami z wykorzystaniem polecenia Sweep (np. przeciągnięcie odcinka po liniach śrubowych globoidalnych) jest najmniej pracochłonne, ale otrzymuje się zarys wklęsły. Największa wklęsłość wynosi 0,01 mm. Do poglądowych analiz, np. śladu styku metodą geometryczną, można wykorzystać taki model. Natomiast do dokładnych lepiej posługiwać się modelem wykonanym metodą wieloprzekrojową.

Błąd między metodami jest mniejszy od dokładności wykonania rzeczywistego ślimaka globoidalnego.

Wirtualny model CAD jest niezbędny w trendach współczesnego projektowania. Przed wykonaniem części, systemy CAD pozwalają przeprowadzić wiele analiz, np. obliczenia MES, wyznaczyć geometrycznie ślad styku współpracującej przekładni.

References

1. Połowniak P., M. Sobolak. 2015. „Modelowanie ślimaka globoidalnego w środowisku CAD”. Mechanik 01: 71-74. [In Polish: „Modeling of globoid worm gearing in CAD”].

2. Sobolak M. 2006. Analiza i synteza współpracy powierzchni kół zębatych metodami dyskretnymi. Rzeszów: Oficyna Wydawnicza Politechniki Rzeszowskiej. [In Polish: Analysis and synthesis of cooperation surface gears discrete methods].

Received 17.04.2015; accepted in revised form 19.09.2015

Scientific Journal of Silesian University of Technology. Series Transport is licensed under a Creative Commons Attribution 4.0 International License

---

[1] Faculty of Mechanical Engineering and Aeronautics, Rzeszow University of Technology, al. Powstańców Warszawy 8, 35-959 Rzeszów, Poland. E-mail: ppolowniak@prz.edu.pl