Article citation info:

Noga, S., Markowski, T., Bogacz, R. Method of determining the normal modes of toothed gears with complex geometry. Scientific Journal of Silesian University of Technology. Series Transport. 2015, 89, 119-127. ISSN: 0209-3324. DOI: 10.20858/sjsutst.2015.89.13.

Stanisław NOGA[1], Tadeusz MARKOWSKI[2], Roman BOGACZ[3]

METHOD OF DETERMINING THE NORMAL MODES OF TOOTHED GEARS WITH COMPLEX GEOMETRY

Summary. This work deals with transversal vibrations of the toothed gear, which is discussed as an annular plate with a complex geometry. The procedure for determining the proper distorted normal modes of vibrations of the wheel with discontinuous geometry is discussed. The required models are created by means of the finite element method. The pre–stress effect is included by means of the ANSYS code. The problem of modelling utilizing cyclic symmetry of the system under study is discussed. It is important to note that the issues presented in this work have a practical value for design engineers dealing with the dynamics of rotating systems.

Keywords: normal modes, toothed gears, complex geometry

METODA OZNACZANIA FORM WŁASNYCH KÓŁ ZĘBATYCH O ZŁOŻONYM KSZTAŁCIE

Streszczenie. W pracy analizowane są drgania poprzeczne koła zębatego, rozważanego jako płyta pierścieniowa o złożonym kształcie. Omówiono procedurę oznaczania postaci drgań własnych koła, ulegających deformacji z powodu zaburzonej geometrii układu. Wymagane do analizy modele obliczeniowe opracowano z wykorzystaniem metody elementów skończonych. W obliczeniach uwzględniono wpływ prędkości kątowej koła na wartości częstości drgań własnych. Omówiono także zagadnienia związane z uwzględnieniem własności cyklicznej symetrii układu. Obliczenia numeryczne wykonano w programie ANSYS. Prezentowane zagadnienia mogą być pomocne inżynierom, zajmującym się zagadnieniami wirujących układów mechanicznych.

Słowa kluczowe: formy własne, koła zębate, złożony kształt

1. WPROWADZENIE

Zagadnienia drgań poprzecznych płyt kołowych i pierścieniowych są przedmiotem zainteresowania szerokiego kręgu badaczy oraz ośrodków badawczo–rozwojowych [1, 3-8]. Wynika to z faktu, że niektóre obracające lub toczące się elementy maszyn (np. koła zębate, koła kolejowe) mogą być traktowane jako płyty kołowe lub pierścieniowe, o geometrii wynikającej z konstrukcji wymienionych układów [1, 7]. Częste przypadki uszkodzeń wirujących zespołów wynikają z pojawiających się w czasie pracy dodatkowych obciążeń dynamicznych, będących skutkiem drgań. Z tego też względu na etapie projektowania ważne jest ustalenie przedziału wartości częstości własnych wirujących zespołów. Badania drgań poprzecznych płyt kołowych zapoczątkował Ernst Chladni, opracowując metodę (tzw. metoda smyczkowa) wyznaczania linii węzłowych swobodnych płyt kołowych i kwadratowych [8]. Zagadnienia drgań poprzecznych kół zębatych, modelowanych płytami pierścieniowymi z uwzględnieniem wirowania, rozważano w pracach [1, 3-7]. W rozdziale monografii [2] omówiono między innymi drgania stoisk do badań doświadczalnych w warunkach pracy, kół zębatych wysokoobrotowych przekładni lotniczych.

W niniejszym artykule rozważania dotyczą w głównej mierze omówienia procedury oznaczania postaci drgań własnych poprzecznych koła zębatego, ulegających deformacji z powodu nieciągłej geometrii układu. W rozważaniach uwzględnione zostaną zjawiska wynikające z ruchu obrotowego koła z zadaną prędkością kątową. W procesie modelowania wykorzystano własności cyklicznej symetrii układu. W pewnym zakresie zagadnienia identyfikacji zdeformowanych postaci drgań własnych kół o złożonej geometrii omówiono w pracach [1, 3, 5]. Referat jest kontynuacją prac Autorów, dotyczących drgań poprzecznych kół zębatych przekładni lotniczych.

2. Sformułowanie Problemu

Zasadniczym celem pracy jest omówienie działania procedury identyfikacji postaci drgań własnych poprzecznych wybranego koła zębatego, modelowanego płytą pierścieniową z otworami przelotowymi. Rozważania prowadzi się dla koła zębatego pokazanego na rysunku 1a. Takie rozwiązanie jest często stosowane w wysokoobrotowych przekładniach zębatych wykorzystywanych w układach lotniczych. Do dalszej analizy przyjmuje się modele uproszczone koła (rys. 1b–c), w których pomija się geometrię zębów. Sposoby tworzenia uproszczonych modeli kół zębatych omówiono szerzej w pracy [7]. Zaproponowane uproszczenie pozwoli w dalszych rozważaniach uwzględnić własności cyklicznej symetrii układu (rys. 1c). Ma to istotne znaczenie przy budowie, wymaganych w procesie analizy, modeli numerycznych metody elementów skończonych (MES).

b)

c)

a)

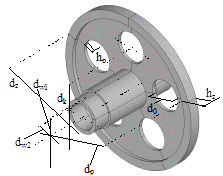
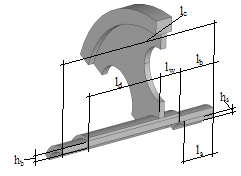
Rys. 1. Modele geometryczne: (a) model koła zębatego, (b) model uproszczony pełny, (c) model uproszczony z cykliczną symetrią

Wymiary geometryczne przyjętego do analizy układu (średnice: d_z, d₀, d_p, d_k, d_w1, d_w2; grubości: h_p, h_z, h_b, h_s; długości: l_b, l_c, l_d, l_s, l_w) zdefiniowano, jak pokazano na rysunku 1b–c. Rozważany układ składa się z płyty pierścieniowej z wieńcem, osadzonej na drążonym stopniowanym wale. Płyta ma nieciągłości geometryczne w postaci przelotowych otworów, umiejscowionych na zadanym promieniu (rys. 1a-b). Zagadnienie drgań własnych omawianego układu rozwiązano metodą elementów skończonych. Ze względu na symetrię kołową układu dla każdego rozwiązania, dla którego linie węzłowe tworzą średnice węzłowe, otrzymuje się dwa identyczne układy prostych węzłowych, obróconych względem siebie o kąt α = π/(2n), przy czym n to liczba średnic węzłowych.

Tablica 1 Dane konstrukcyjne analizowanego układu
	d_z [mm]	d_p [mm]	d_k [mm]	d_w1 [mm]	d_w2 [mm]	d₀ [mm]	h_z [mm]	h_p [mm]	h_b [mm]
	110	98	62.7	26.7	18.8	22.4	7	2.3	2.6
	h_s [mm]	l_b [mm]	l_c [mm]	l_d [mm]	l_s [mm]	l_w [mm]		E [MPa]	 [kg/m³]
	1.8	14.9	66.7	31.4	12.7	8.9	0.3	2.08·10⁵	7.83·10³

Zgodnie z przyjętymi standardami w teorii płyt kołowych i pierścieniowych, w niniejszej pracy, częstości własne oznaczono przez ω_mn, gdzie m to liczba okręgów węzłowych, a n to wspomniana wcześniej liczba średnic węzłowych. Ze względu na złożony kształt koła postacie giętne układu ulegają znacznej deformacji w porównaniu do układu pozbawionego otworów, co powoduje, że w odniesieniu do niektórych rezultatów trudno jest jednoznacznie określić, jakiej formy własnej dotyczą. Problem się dodatkowo komplikuje, jeżeli zmianie ulega prędkość kątowa koła. Do identyfikacji postaci wykorzystano procedurę oznaczania form drgań giętnych, pozwalającą ustalić odpowiedniość między formami drgań koła z pełną tarczą i koła z otworami przelotowymi w tarczy. Na potrzeby procedury przyjmuje się model pomocniczy tarczy koła z wieńcem o kształcie podanym na rys. 2b.

b)

a)

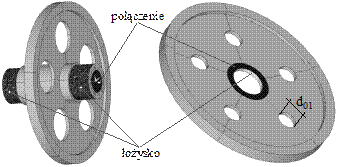
Rys. 2. Warunki brzegowe (a) i model pomocniczy (b)

Parametry geometryczne modelu pomocniczego przyjęto z geometrii analizowanego koła (rys. 1b-c). Istotne będą w tym przypadku: średnica zewnętrzna d_z, średnica pod wieńcem d_p, średnica wewnętrzna d_w2, grubość h_p oraz h_z (tabl. 1). W dalszej kolejności prowadzi się analizę dynamiczną dla przypadków modeli pomocniczych, obracających się z zadaną prędkością kątową, w których wartość średnicy otworów przelotowych d₀₁ (rys. 2b) zmienia się zgodnie z tablicą 2. Otrzymane rezultaty porównuje się jakościowo i ilościowo.

Tablica 2

Średnice otworów modelu pomocniczego

	Model pomocniczy
	1	2	3	4	5	6	7	8
d₀₁ [mm]	5	6.72	7	7.28	8.4	11.2	15.68	22.4

Proponowana procedura pozwala prześledzić deformację linii węzłowych spowodowaną otworami przelotowymi w tarczy koła i w konsekwencji ustalić odpowiedniość między postaciami drgań koła z pełną tarczą i koła z otworami w tarczy. W ostatnim kroku porównuje się wyniki uzyskane dla modelu pomocniczego z rezultatami dla układu pokazanego na rysunku 1b (model uproszczony pełny). Dane konstrukcyjne analizowanego układu zamieszczono w tablicy 1.

3. Analiza Numeryczna

Jak wspomniano wcześniej, rozważania prowadzi się z wykorzystaniem modelu koła z pominiętą geometrią zębów. Pozwala to w znacznym stopniu ograniczyć liczbę elementów skończonych w modelach MES układu. Do obliczeń przyjęto element czworościenny, dziesięciowęzłowy (solid187), izotropowy o trzech stopniach swobody w każdym węźle. Wymagane do obliczeń modele MES opracowano w środowisku obliczeniowym ANSYS. W procesie analizy stosujemy dwa modele MES rozważanego koła.

b)

a)

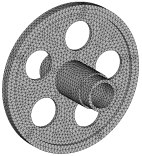
Rys. 3. Model podstawowy MES układu (a) i model MES z cykliczną symetrią układu (b)

Pierwszy opracowany model (tzw. model podstawowy) pokazano na rysunku 3a. Model zawiera 19725 elementów oraz 36248 węzłów. Drugi model MES opracowano z uwzględnieniem własności cyklicznej symetrii układu. Geometrycznie drugi model stanowi jedną piątą część modelu podstawowego MES (rys. 3b). Model ten zawiera 3984 elementy skończone. We wszystkich analizowanych modelach (łącznie z modelami pomocniczymi MES) warunki brzegowe przyłożono do węzłów. W każdym modelu MES węzłom leżącym na powierzchni oznaczonej łożysko (rys. 2a-b) odebrano jeden stopień swobody związany z przemieszczeniem promieniowym węzłów. Z kolei węzłom leżącym na powierzchni oznaczonej jako połączenie (rys. 2a-b) odebrano jeden stopień swobody związany z przemieszczeniem węzłów wzdłuż osi symetrii każdego modelu. Ponadto, w drugim modelu MES występują warunki brzegowe, uwzględniające cykliczną symetrię układu. Dla tak opracowanych modeli MES prowadzono analizę numeryczną do momentu wyznaczenia częstości własnej ω₁₈. Obliczenia wykonano, przy założeniu że układy obracają się z prędkościami odpowiednio 80 [rad/s] i 1047 [rad/s]. Efekt wirowania uwzględniono, wyznaczając dla każdego przypadku modelu w pierwszym kroku obliczeniowym związanym z analizą statyczną rozkład naprężeń, wynikający z ruchu obrotowego koła. Następnie uzyskany rozkład wykorzystano w kolejnym kroku obliczeniowym związanym z analizą modalną.

W dalszej kolejności przedstawiono wybrane wyniki analizy numerycznej, pozwalające potwierdzić skuteczność omawianej procedury identyfikacji postaci drgań własnych poprzecznych koła. W pierwszej kolejności pokazane są zdeformowane postacie własne (rys. 4-5), do identyfikacji których konieczne było zastosowanie procedury oznaczania postaci drgań własnych. W prezentowanych rozwiązaniach daje się zauważyć znaczne deformacje linii węzłowych, związanych z okręgami i średnicami węzłowymi. Warto też podkreślić, że we wszystkich omawianych przypadkach występuje znaczna zgodność pomiędzy kształtem form wygenerowanych z pierwszego i drugiego modelu MES układu.

c)

b)

a)

Rys. 4. Postacie drgań odpowiadające częstościom: (a) ω₁₆; (b) ω₃₁; (c) ω₂₅; (model podstawowy)

c)

b)

a)

Rys. 5. Postacie drgań odpowiadające częstościom: (a) ω₁₆; (b) ω₃₁; (c) ω₂₅; (model z cykliczną symetrią)

W niniejszej pracy model MES z cykliczną symetrią traktujemy jako przybliżenie modelu pełnego MES. Dokładność modeli z cykliczną symetrią względem modeli pełnych ustala się wyznaczając błąd względny częstości, określony zależnością:

(1)

gdzie:

ω^c – częstotliwość własna z modelu MES z cykliczną symetrią [Hz];

ω^p – częstotliwość własna z modelu pełnego MES (podstawowego) [Hz].

Tablica 3 Wartości częstotliwości własnych oraz błąd częstości
θ [rad/s]	ω₁₆ [Hz]	ω₃₁ [Hz]	ω₂₅ [Hz]
Model podstawowy
80	16949	18767	26633
1047	16968	18785	26658
Model z cykliczną symetrią
80	16948	18768	26635
1047	16967	18786	26660
Błąd częstości
θ [rad/s]	ε₁₆ [%]	ε₃₁ [%]	ε₂₅ [%]
80	-0.006	-0.005	0.008
1047	-0.006	0.005	0.008

W tablicy 3 zamieszczono wartości częstotliwości własnych odnoszące się do postaci własnych prezentowanych na rysunkach 4 i 5 oraz błędy częstości wynikające z porównania wyników. Wartości te wyznaczono dla dwóch różnych prędkości kątowych układu, tj. dla θ = 80 [rad/s] oraz dla θ = 1047 [rad/s]. Podobnie jak w przypadku postaci drgań własnych, we wszystkich omawianych przypadkach występuje znaczna zgodność odpowiednich wartości częstotliwości własnych wygenerowanych z obu modeli MES układu.

Kolejne prezentowane rezultaty dotyczą procedury oznaczania zdeformowanych postaci drgań własnych układu. Podobnie jak dla koła, w procesie analizy stosujemy dwa rozwiązania w zakresie budowy modeli pomocniczych MES. W pierwszym rozwiązaniu modele pomocnicze MES wygenerowano na podstawie pełnych modeli geometrycznych (rys. 2b). Oznaczymy je jako tzw. modele pomocnicze MES pełne. W drugim rozwiązaniu uwzględniono własności cyklicznej symetrii modeli pomocniczych. W tym rozwiązaniu każdy model pomocniczy MES stanowi jedną piątą część modelu pomocniczego MES pełnego. Będziemy je określać jako modele pomocnicze MES z cykliczną symetrią.

Tablica 4 Wartości częstotliwości własnych oraz błąd częstości (modele pomocnicze)
	1	2	3	4	5	6	7	8
Modele pomocnicze pełne
ω₁₆ [Hz]	17490	17460	17437	17421	17359	17122	16752	16941
ω₃₁ [Hz]	17596	17557	17531	17523	17519	17552	17814	18879
ω₂₅ [Hz]	19732	19795	19791	19815	19955	20582	22453	26108
Modele pomocnicze z cykliczną symetrią
ω₁₆ [Hz]	17489	17456	17431	17419	17341	17105	16741	16933
ω₃₁ [Hz]	17568	17545	17521	17519	17507	17543	17805	18863
ω₂₅ [Hz]	19725	19787	19785	19808	19946	20572	22435	26071
Błąd częstości
ε₁₆ [%]	-0.006	-0.023	-0.034	-0.012	-0.104	-0.099	-0.066	-0.047
ε₃₁ [%]	-0.159	-0.068	-0.057	-0.023	-0.069	-0.051	-0.051	-0.085
ε₂₅ [%]	-0.036	-0.04	-0.03	-0.035	-0.045	-0.049	-0.08	-0.142

Rys. 6. Postacie drgań odpowiadające częstości ω₁₆ (model pomocniczy MES pełny)

Rys. 7. Postacie drgań odpowiadające częstości ω₁₆ (model pomocniczy MES pełny)

W tablicy 4 zamieszczono wyniki obliczeń, odnoszące się do modeli pomocniczych MES pełnych i z cykliczną symetrią, wykorzystanych w procedurze oznaczania form własnych wymienionych wcześniej częstości własnych. Prezentowane rezultaty wygenerowano, przy założeniu że prędkość kątowa wynosi θ = 80 [rad/s].

Rys. 8. Postacie drgań odpowiadające częstości ω₃₁ (model pomocniczy MES pełny)

Rys. 9. Postacie drgań odpowiadające częstości ω₃₁ (model pomocniczy MES pełny)

Wyniki prezentowane na rys. 6-10 uzyskano przy użyciu modeli pomocniczych MES pełnych. Z kolei postacie własne pokazane na rysunku 11 otrzymano z modeli pomocniczych MES z cykliczną symetrią.

Rys. 10. Postacie drgań odpowiadające częstości ω₂₅ (model pomocniczy MES pełny)

Rys. 11. Postacie drgań odpowiadające częstości ω₂₅ (model pomocniczy MES z cykliczną symetrią)

Przedstawione na rys. 6-11 wyniki pozwalają prześledzić deformację linii węzłowych, związanych z okręgami i średnicami węzłowymi, ze względu na zmianę średnicy otworów przelotowych. Zauważa się znaczne różnice kształtu form odnoszących się do dyskutowanych częstości własnych. Warto podkreślić, że do identyfikacji poszczególnych form nie jest wymagana taka sama liczba modeli pomocniczych (rys. 10). Analizując otrzymane wyniki, zauważa się nieznaczne różnice pomiędzy wartościami poszczególnych częstotliwości własnych otrzymanych odpowiednio z modeli pełnych i z modeli z cykliczną symetrią (tablica 4). Ponadto, występuje znaczna zgodność kształtu form otrzymanych z modeli pomocniczych pełnych i postaci otrzymanych z modeli z cykliczną symetrią.

4. Uwagi i WNIOSKI

Projektowanie wirujących zespołów współczesnych konstrukcji mechanicznych wymaga stosowania zaawansowanych technik komputerowych, wykorzystujących między innymi metodę elementów skończonych. Dotyczy to w szczególności urządzeń związanych z przemysłem lotniczym. W niniejszej publikacji analizowano drgania poprzeczne koła zębatego wysokoobrotowej przekładni lotniczej, rozważanego jako płyta pierścieniowa o złożonym kształcie. Omówiono procedurę oznaczania zdeformowanych postaci drgań własnych układu. W procedurze uwzględniono własności wynikające z cyklicznej symetrii układu. Prezentowane wyniki potwierdziły atrakcyjność stosowania technik obliczeniowych, wykorzystujących własności cyklicznej symetrii układu, w analizie drgań złożonych układów wirujących. Stosowana technika pozwala w znacznym stopniu ograniczyć liczbę elementów skończonych modelu MES analizowanego układu. Prezentowane w niniejszej pracy zagadnienia mogą być pomocne inżynierom, zajmującym się analizą drgań wirujących układów mechanicznych.

References

1. Bogacz R., S. Noga. 2012. “Free transverse vibration analysis of a toothed gear”. Archive of Applied Mechanics 82: 1159-1168.

2. Markowski T., S. Noga, S. Rudy. 2011. Modelling and vibration analysis of some complex mechanical systems. In Recent advances in vibrations, edited by N. Baddour (red). Rijeka: Intech open access publisher.

3. Noga S. 2008. „Analiza drgań poprzecznych koła zębatego”. Czasopismo Techniczne Mechanika 9–M: 85-94. [In Polish: “Vibration analysis of transverse gear”].

4. Noga S. 2014. “Transverse vibration analysis of a compound plate with using cyclic symmetry modeling”. Vibrations in Physical System XXVI: 211-216.

5. Noga S., R. Bogacz. 2013. “Algorithm to identify the mode shapes of the circular or annular systems with the discontinuous features”. In Proceedings of the 20^th International Conference on Computer Methods in Mechanics. Poznań, August 27–31, 2013. MS07–5–6.

6. Noga S., R. Bogacz. 2011. „Analiza deformacji wybranych postaci drgań własnych koła zębatego”. Czasopismo Techniczne Mechanika 2(1–M): 155-165. [In Polish: „Analysis of deformation mode shapes selected gear”].

7. Noga S., R. Bogacz, K. Frischmuth. 2012. “Vibration analysis of toothed gear with cyclic symmetry modelling”. Vibrations in Physical System XXV: 299-304.

8. Waller M. 1961. Chladni figures, a study in symmetry. London: G. Bell and Sons LTD.

Received 11.05.2015; accepted in revised form 21.09.2015

Scientific Journal of Silesian University of Technology. Series Transport is licensed under a Creative Commons Attribution 4.0 International License

[1] Faculty of Mechanical Engineering and Aeronautics, Rzeszow University of Technology, al. Powstańców Warszawy 12, 35-959 Rzeszów, Poland. E-mail: noga@prz.edu.pl

[2] Faculty of Mechanical Engineering and Aeronautics, Rzeszow University of Technology, al. Powstańców Warszawy 12, 35-959 Rzeszów, Poland. E-mail: tmarkow@prz.edu.pl

[3] Faculty of Automotive and Construction Machinery Engineering, Warsaw University of Technology, ul. Narbutta 84, 02–524 Warsaw, Poland. E-mail: rbogacz@ippt.pan.pl