Article citation info:

Markowski, T., Batsch, M. Influence of Novikov convexo-concave gear parameters on contact pattern. Scientific Journal of Silesian University of Technology. Series Transport. 2015, 89, 89-99. ISSN: 0209-3324. DOI: 10.20858/sjsutst.2015.89.10.

 

 

Tadeusz MARKOWSKI[1], Michał BATSCH[2]

 

 

 

INFLUENCE OF NOVIKOV CONVEXO-CONCAVE GEAR PARAMETERS ON CONTACT PATTERN

 

Summary. Thesis presents the results of simulations, aiming at examining the influence of chosen Novikov gear parameters on its contact region. The parameters which influence have been established include the overlap ratio, ratio of radius of teeth profiles, ratio of convex tooth profile radius to pitch radius, normal pressure angle, translation of convex tooth profile along the contact line and axes distance error. Knowledge of the influence of gear parameters on its contact pattern enable to efficient establishing these parameters, which allows to compensate assembly errors or edge contact.

Keywords: Novikov convexo-concave gear, contact pattern, compensate, gear parameters, deviation

 

 

 

WPŁYW PARAMETRÓW PRZEKŁADNI ZĘBATYCH O KOŁOWO-ŁUKOWYM ZARYSIE ZĘBÓW TYPU NOWIKOWA NA ŚLAD STYKU

 

Streszczenie. Artykuł przedstawia wyniki symulacji, dzięki którym wyznaczono wpływ parametrów przekładni Nowikowa na jej ślad styku. Wśród parametrów, których wpływ był badany, wyróżnić można: poskokowy wskaźnik przyporu, stosunek promieni zarysów, stosunek promienia zarysu zęba zębnika do jego promienia podziałowego, normalny kąt przyporu, przesunięcie środka zarysu zęba wypukłego wzdłuż linii przyporu oraz błąd rozstawienia osi kół. Znajomość wpływu parametrów przekładni na jej obszar styku umożliwia bardziej efektywny ich dobór pozwalający między innymi na kompensację błędów wynikających z montażu czy uniknięcie negatywnego efektu krawędziowania.

Słowa kluczowe: przekładna zębata Nowikowa o kołowo-łukowym zarysie zębów,  ślad styku, kompensacja, parametry przekładni, odchyłki

 

 

1.      WPROWADZENIE

 

Przekładnie zębate o wklęsło-wypukłym zarysie zębów typu Nowikowa odznaczają się większą nośnością powierzchniową od przekładni ewolwentowych. Były one przedmiotem analiz teoretycznych [1, 2, 3, 4, 5, 6, 7, 11, 14] i badań doświadczalnych [9, 10, 13] prowadzonych przez badaczy na całym świecie. Istnieją przykłady zastosowań tego typu uzębień, które pozwoliły na zwiększenie nośności [12] lub zmniejszenie masy [6, 7, 8] przekładni.

Przekładnia zębata typu Nowikowa definiowana jest przez wiele parametrów. Znajomość ich wpływu na kształt, położenie oraz pole powierzchni śladu styku pozwala projektantowi na optymalny dobór geometrii przekładni, która zapewni prawidłowe położenie śladu styku.

W niniejszym artykule analizowana była przekładnia Nowikowa z jedną linią styku o parametrach podanych w tablicy 1. Ślady styku wyznaczone zostały za pomocą metody, w której odległość pomiędzy powierzchniami bocznymi zębów mierzona była wzdłuż wersora normalnego [2, 3, 4, 15] dla grubości znacznika 0,005 mm.

 

Tablica 1

Parametry analizowanej przekładni Nowikowa

Parametr

Zębnik

Koło

Moduł normalny [mm]

mn=3

Liczba zębów [-]

z1=23

z2=56

Poskokowy wskaźnik przyporu [-]

εβ=1,2157

Szerokość wieńca [mm]

b=36

Kąt pochylenia linii zęba []

β=18,5584

Normalny kąt przyporu [

αn=20

Przesunięcie zarysu zęba wklęsłego [mm]

dCO’=0

Zarys

wypukły

wklęsły

Promień zarysu [mm]

ρ1=6,5506

ρ2=6,7799

Średnica podziałowa [mm]

d1=72,7848

d2=177,2152

Średnica wierzchołków [mm]

da1=79,6848

da2=177,2152

Średnica stóp [mm]

df1=71,2848

df2=169,4152

2.      WPŁYW POSKOKOWEJ LICZBY PRZYPORU

 

W celu zapewnienia ciągłości zazębienia przekładni Nowikowa poskokowa liczba przyporu musi być większa od jedności. Ustalenie wartości tego parametru wiąże się z doborem odpowiedniego kąta pochylenia linii zęba. Wraz z jego wzrostem zwiększa się różnica pomiędzy średnimi promieniami krzywizn powierzchni bocznych zębów w punkcie styku. Rysunek 1 przedstawia wpływ poskokowej liczby przyporu na kształt oraz położenie śladu styku.

 

 

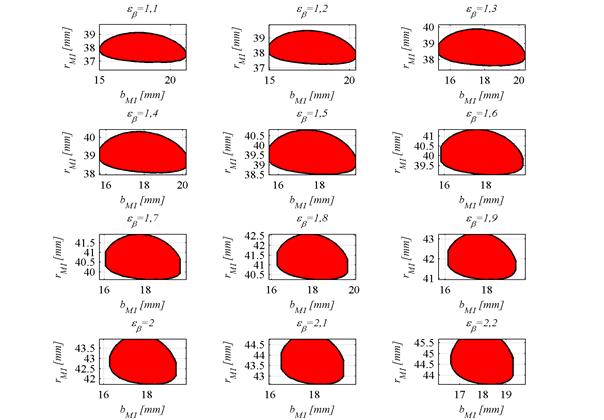
Rys. 1. Wpływ poskokowej liczby przyporu

 

Obszar styku przyjmuje kształt zbliżony do elipsy. Dla małych wartości poskokowego stopnia pokrycia jej oś wielka ułożona jest wzdłuż linii zęba (stosunek osi wielkiej do osi małej jest większy od 1). W miarę wzrastania parametru εβ ślad ulega zwężeniu, natomiast oś wielka staje się osią małą (stosunek uprzedniej osi wielkiej do nowej osi wielkiej jest mniejszy od 1). Dla dużych wartości poskokowego stopnia pokrycia 1,9÷2,2 ślad przesunięty jest w stronę głowy zęba wypukłego. Sytuacja ta jest niekorzystna ze względu na możliwość jej wykruszania się oraz podcięcia stopy zęba wklęsłego.

Rysunek 2 przedstawia zależność pola obszaru styku od poskokowego wskaźnika przyporu.

 

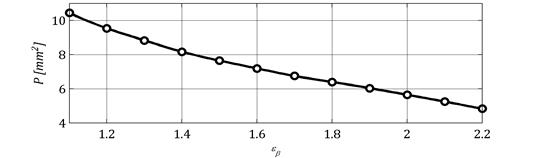
Rys. 2. Zależność pola powierzchni obszaru styku od poskokowej liczby przyporu

 

W miarę wzrostu εβ pole śladu styku zmniejsza się. Rośnie natomiast ilość zębów współpracujących w danej chwili, a co za tym idzie rośnie pole powierzchni łącznego śladu styku. Przy doborze poskokowej liczby przyporu należy również kierować się wartością kąta pochylenia linii zęba, która ze względu na występujące siły poosiowe nie może być za duża.

 

 

3.      WPŁYW STOSUNKU PROMIENI ZARYSÓW

 

Jak wynika z przeprowadzonych symulacji, parametrem, który wywiera istotny wpływ na obszar styku przekładni Nowikowa, jest stosunek promieni zarysów zęba wklęsłego i wypukłego ρ2/ρ1. Parametr ten znacząco wpływa na średni promień krzywizny zęba w punkcie styku. Rysunek 3 przedstawia wpływ stosunku ρ2/ρ1 na kształt śladu styku przekładni. Dla małej wartości ρ2/ρ1=1,005 obszar styku jest duży i rozciąga się na całej wysokości zęba. Jego kształt można opisać jako obszar ograniczony dwiema prostymi oraz dwiema krzywymi, mającymi punkt przegięcia w połowie wysokości zęba. W miarę wzrostu stosunku ρ2/ρ1 ślad styku przyjmuje kształt obszaru ograniczonego parabolą (z ramionami skierowanymi ku stopie zęba wypukłego) oraz prostą (obszar z rysunku 3 dla ρ2/ρ1=1,015). Dalszy wzrost wartości ρ2/ρ1 skutkuje powstaniem eliptycznego śladu styku. Z rysunku 3 wynika również stałość położenia śladu styku na powierzchni bocznej zęba w zakresie ρ2/ρ1=1,005÷1,055.

 

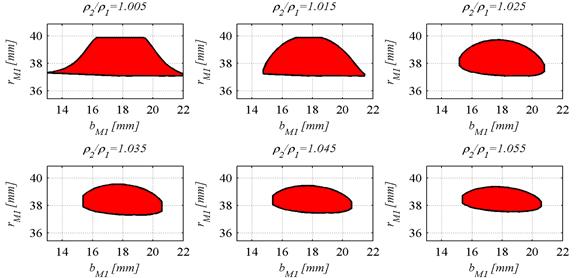
Rys. 3. Wpływ stosunku promieni zarysów

 

 

Rysunek 4 przedstawia zależność pola powierzchni obszaru styku od stosunku promieni zarysów ρ2/ρ1.

Pole powierzchni maleje od wartości maksymalnej dla ρ2/ρ1=1,005 do wartości minimalnej dla ρ2/ρ1=1,055.

 

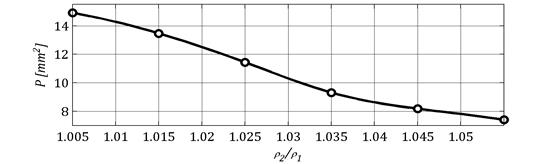
Rys. 4. Zależność pola powierzchni obszaru styku od stosunku promieni zarysów zębów

 

 

4.      WPŁYW STOSUNKU PROMIENIA ZARYSU DO PROMIENIA PODZIAŁOWEGO

 

Parametrem, który również wpływa na geometrię zarysu zębów przekładni Nowikowa, jest stosunek promienia zarysu zęba wypukłego do promienia podziałowego zębnika. Stosunek ten dla określonej średnicy podziałowej definiuje promień zarysu zęba wypukłego. Jak wynika z przeprowadzonych analiz, jego wartość wpływa zarówno na położenie, jak i na pole powierzchni obszaru styku, co pokazano na rysunku 5.

 

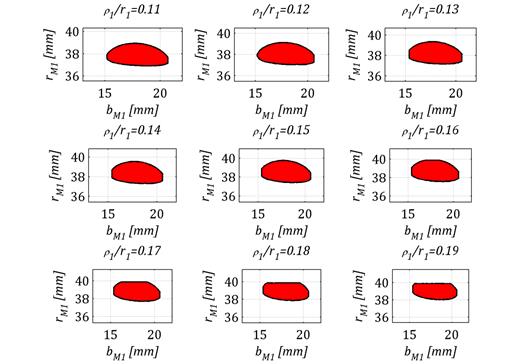
Rys. 5. Wpływ stosunku promienia zarysu zęba wypukłego
do promienia podziałowego zębnika

 

Począwszy od minimalnej wartości ρ1/r1=0,11 do wartości ρ1/r1=0,19 obszar styku przyjmuje kształt eliptyczny oraz przesuwa się ku głowie zęba wypukłego.

Rysunek 6 przedstawia zależność pola powierzchni śladu styku od stosunku ρ1/r1.

 

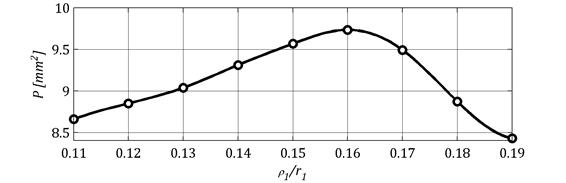
Rys. 6. Zależność pola powierzchni śladu styku od stosunku promienia zarysu do promienia podziałowego

 

Wraz ze wzrostem wartości analizowanego parametru wartość pola powierzchni wzrasta do maksymalnej wartości dla ρ2/r1=0,16, a następnie spada, aby osiągnąć minimum przy ρ2/r1=0,19.

 

 

5.      WPŁYW NORMALNEGO KĄTA PRZYPORU

 

Istotnym parametrem, który należy dobrać podczas projektowania przekładni Nowikowa, jest normalny kąt przyporu. Jak wynika z przeprowadzonych symulacji, pole obszaru styku oraz jego położenie silnie od niego zależy. Na rysunku 7 przedstawiono wpływ normalnego kąta przyporu na obszar styku przekładni.

Im wartość kąta przyporu jest mniejsza, tym ślad styku jest bardziej przesunięty w kierunku stopy zęba o zarysie wypukłym. W miarę wzrastania kąta przyporu ślad styku przesuwa się natomiast ku głowie zęba wypukłego. Dla małych wartości kąta przyporu obszar styku przyjmuje kształt fragmentu elipsy utworzonego przez jej przecięcie z osią równoległą do jej osi wielkiej (rysunek 6 obszar styku dla αn=10°). Ta postać śladu styku jest szczególnie niekorzystna ze względu charakter obciążenia zęba wklęsłego. Siła skupiona jest wówczas u jego wierzchołka, co może skutkować miejscowym wykruszeniem się zęba. Ponadto wystąpić może podcinanie zęba wypukłego przez ząb wklęsły. Im większy jest kąt przyporu, kształt obszaru styku zmienia się w kształt zbliżony do elipsy.

Rysunek 8 przedstawia zależność pola powierzchni obszaru styku od kąta przyporu.

 

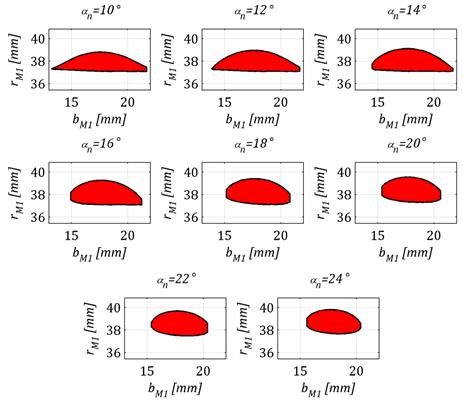
Rys. 7. Wpływ normalnego kąta przyporu

 

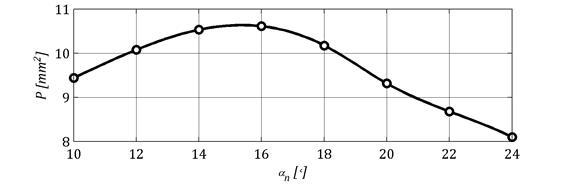
Rys. 8. Zależność pola powierzchni obszaru styku od normalnego kąta przyporu

 

Wraz ze wzrostem kąta przyporu pole powierzchni wzrasta do momentu, w którym osiągnie swoje maksimum dla kąta αn=16°. Następnie jego wartość spada, aby dla kąta αn=24° przyjąć wartość minimalną.

 

 

6.      WPŁYW PRZESUNIĘCIA ZARYSU ZĘBA WYPUKŁEGO

 

Kolejnym parametrem definiującym geometrię zazębienia typu Nowikowa jest przesunięcie zarysu zęba wypukłego wzdłuż linii przyporu. Rysunek 9 przedstawia wpływ przesunięcia środka zarysu zęba wypukłego na ślad styku przekładni.

 

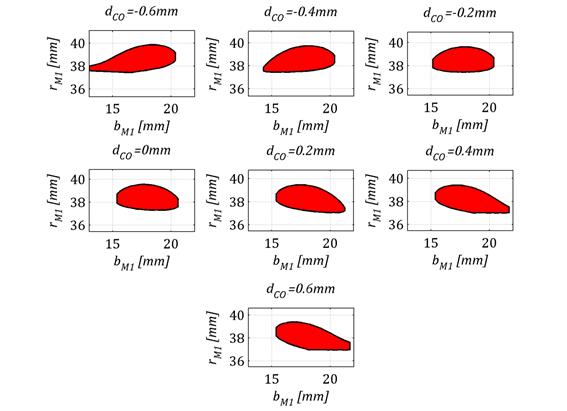
Rys. 9. Wpływ przesunięcia zarysu zęba wypukłego

 

Dla jego ujemnych wartości obszar styku przyjmuje kształt zniekształconej elipsy, która zwęża się w ujemnym kierunku osi odciętych. Dla dodatnich wartości zwężenie to występuje po dodatniej stronie osi odciętych. Ponadto, dla małych lub dużych wartości przesunięcia obszar styku krawędziuje.

Na rysunku 10 przedstawiono zależność pola powierzchni obszaru styku od przesunięcia zarysu zęba wypukłego.

 

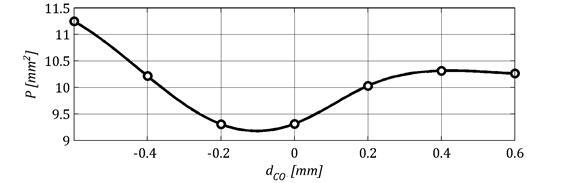
Rys. 10. Zależność pola powierzchni obszaru styku od przesunięcia zarysu zęba wypukłego

 

Pole powierzchni śladu styku jest największe dla skrajnych wartości przesunięcia zarysu. W miarę wzrostu tego parametru pole powierzchni maleje do minimalnej wartości, a następnie rośnie.

7.      WPŁYW BŁĘDU ROZSTAWIENIA OSI KÓŁ

 

Istotnym parametrem mającym duży wpływ na poprawność pracy przekładni Nowikowa jest błąd rozstawienia osi jej kół. Rysunek 11 przedstawia wpływ błędu rozstawienia osi kół przekładni na jej ślad styku.

 

 

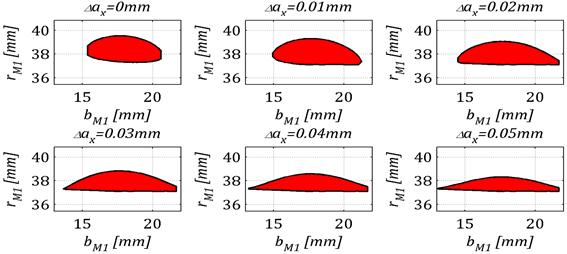
Rys. 11. Wpływ błędu rozstawienia osi kół przekładni Nowikowa na jej ślad styku

 

Im błąd rozstawienia osi kół jest większy, tym obszar styku przesuwa się ku stopie zęba zębnika. Dla analizowanej przekładni od wartości błędu 0,02 mm ślad styku krawędziuje. Sytuacja ta jest niekorzystna ze względu na możliwość wykruszania się głowy zęba koła.

Na rysunku 12 przedstawiono zależność pola powierzchni śladu styku od błędu rozstawienia osi kół.

 

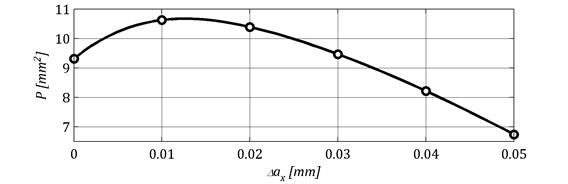
Rys. 12. Zależność pola powierzchni śladu styku od błędu rozstawienia osi kół

 

Im błąd rozstawiania osi kół jest większy, tym pole śladu styku zwiększa się do maksymalnej wartości dla błędu 0,01mm, a następnie spada. W związku z powyższym w pewnym zakresie błąd rozstawienia osi kół przekładni może korzystanie wpływać na jej pracę. Wynika to z obniżenia punktu styku, gdzie stosunek średnich promienia krzywizn jest większy, a co za tym idzie większy jest obszar styku i mniejsze naprężenia stykowe.

8.    PODSUMOWANIE

 

Artykuł przedstawia wyniki wielu symulacji komputerowych, mających na celu zbadanie wpływu wybranych parametrów przekładni na jej obszar styku.

Na ich podstawie stwierdzono, że zmniejszenie stosunku promieni zarysów zębów powoduje wzrost powierzchni obszaru styku, co może zwiększyć nośność powierzchniową pary zębatej. Z drugiej jednak strony może wzrosnąć również wrażliwość przekładni na błąd rozstawienia osi kół. Ponadto zwiększenie stosunku promienia zarysu zęba wypukłego do promienia podziałowego zębnika powoduje przesunięcie śladu styku ku głowie zęba zębnika oraz zmniejszenie jego pola powierzchni, co może być potencjalnie niepożądane. Spadek kąta przyporu obniża punkt styku. Ponadto, istnieje taka wartość tego kąta, dla której pole obszaru styku przyjmuje wartość maksymalną. Im wyższy poskokowy wskaźnik przyporu, tym obszar styku staje się węższy oraz maleje jego pole powierzchni. Przesunięcie zarysu zęba wypukłego powoduje zwiększenie pola powierzchni śladu styku, może jednak prowadzić do jego krawędziowania.

Przekładnie typu Nowikowa są szczególnie wrażliwe na błąd rozstawienia osi kół. Już jego mała wartość powoduje znaczący spadek rzeczywistego kąta przyporu i obniżenie linii styku ku stopie zęba wypukłego. Na etapie projektowania przekładni Nowikowa należy uwzględnić wielkość tego błędu. Efekty nim wywołane można kompensować odpowiednim doborem parametrów, które przesuwają ślad styku ku głowie zęba zębnika, a więc za pomocą normalnego kąta przyporu lub stosunku promienia zarysu do promienia podziałowego. W efekcie po zmontowaniu przekładni obszar styku przyjmie pożądane przez projektanta położenie, a naprężenia stykowe ulegną zmniejszeniu.

 

 

9.    Podziękowania

 

Badania realizowane w ramach Projektu "Nowoczesne technologie materiałowe stosowane w przemyśle lotniczym", Nr POIG.01.01.02-00-015/08-00 w Programie Operacyjnym Innowacyjna Gospodarka (PO IG). Projekt współfinansowany przez Unię Europejską ze środków Europejskiego Funduszu Rozwoju Regionalnego.

 

 

References

 

1.      Batsch M., W. Homik, T. Markowski. 2015. „Cylindrical Gears with Increased Contact Area – Proposal of Application in Watercrafts Power Transmission Systems”. Solid State Phenomena 236: 26-30.

2.      Batsch M., T. Markowski. 2014. „Analityczno-numeryczne metody wyznaczania obszaru styku przekładni wklęsło-wypukłych Nowikowa” Scientific Journal of Silesian University of Technology. Series Transport 82: 155-165. ISSN 0209-3324. [In Polish: “Analytical and numerical methods of determining the contact area convex-concave gear Novikov”].

3.      Batsch M., T. Markowski. 2013. “Analysis of the Contact Region Geometry of the Novikov Convexo-Concave Gears”. In Konferencja AIRTEC 2013. Frankfurt 5-7.10.2013.

4.      Batsch M., T. Markowski. 2013. „Analiza parametrów styku przekładni zębatych o kołowo-łukowym zarysie zębów typu Nowikowa”. Przegląd mechaniczny 7-8: 50-53. [In Polish: „Analysis parameters gears contact with the circular-arc teeth outline the type Novikov”].

5.      Colbourne J.R. 1989. “The Contact Stress in Novikov Gears”. Mechanism and Machine Theory 24(3): 223-229.

6.      Dyson A., H.P. Evans, W. Snidle. 1989. “Wildhaber-Novikov cicrular-arc gears: some properties of relevance to their design”. Proceedings of The Royal Society A Mathematical Physical and Engineering Sciences 425(1825): 341-363.

7.      Dyson A., H.P. Evans, W. Snidle. 1986. “Wildhaber-Novikov circular arc gears: Geometry and Kinematics”. Proceedings of The Royal Society A Mathematical Physical and Engineering Sciences 403(1825): 313-349.

8.      Ellis D.V. 1980. “The Westland Lynx”. The RUSI Journal 125(4): 70-73.

9.      Lingaiah K., K. Ramachandra. 1976. “Photoelastic Optimization of the Profiles of Wildhaber-Novikov Gears”. Experimental Mechanics 16(3): 116-120.

10.  Lingaiah K., K. Ramachandra. 1977. “Three-dimensional Photoelastic Study of the Load-carrying Capacity/Face Width Ratio of Wildhaber-Novikov Gears for Automotive Applications”. Experimental Mechanics 17(10): 392-397.

11.  Litvin F.L., et al. 2002. “New version of Novikov–Wildhaber helical gears: computerized design, simulation of meshing and stress analysis”. Computer methods in applied mechanics and engineering 191(49-50): 5707-5740.

12.  LS Petrochem: LS Pumping Units Catalog. LS Petrochem 2008.

13.  Opitz H., et al. 1965. Der Einfluß der Fertigungsgenauigkeit und der Schmierfilmausbildung auf die Flankentragfähigkeit ungehärteter Stirnräder. Wiesbaden: Springer Fachmedien. [In German: The influence of the manufacturing accuracy and the lubricating film formation on the edge sustainability uncured spur gears].

14.  Tsay C-B., Z.H. Fong. 1989. “The Mathematical Model of Wildhaber-Novikov Gears Applicable to Finite Element Stress Analysis”. Mathematical and Computer Modelling 12(8): 939-946.

15.  Wiktor J. 2004. Analityczno-numeryczne metody analizy parametrów geometrycznych, zakłóceń ruchu i wytrzymałości przekładni walcowych. Rzeszów: Oficyna Wydawnicza Politechniki Rzeszowskiej. [In Polish: Analytical and numerical methods for the analysis of geometrical parameters, traffic disruption and the strength of cylindrical].

 

 

Received 11.05.2015; accepted in revised form 21.09.2015

 

 

Scientific Journal of Silesian University of Technology. Series Transport is licensed under a Creative Commons Attribution 4.0 International License


[1] Faculty of Mechanical Engineering and Aeronautics, Rzeszow University of Technology, al. Powstańców Warszawy 8, 35-959 Rzeszów, Poland. E-mail: tmarkow@prz.edu.pl

[2] Faculty of Mechanical Engineering and Aeronautics, Rzeszow University of Technology, al. Powstańców Warszawy 8, 35-959 Rzeszów, Poland. E-mail: mbatsch@prz.edu.pl