Article citation info:
Kaššay, P., Urbanský, M. Torsional natural frequency tuning by means of
pneumatic flexible shaft couplings. Scientific
Journal of Silesian University of Technology. Series Transport. 2015, 89, 57-60. ISSN: 0209-3324. DOI:
10.20858/sjsutst.2015.89.6.
Peter KAŠŠAY[1],
Matej URBANSKÝ[2]
TORSIONAL NATURAL FREQUENCY
TUNING BY MEANS OF PNEUMATIC FLEXIBLE SHAFT COUPLINGS
Summary. This
article deals with the use of pneumatic flexible shaft couplings as device for
tuning torsional natural frequencies of mechanical systems. These couplings are
using air bellows as flexible elements. Their torsional stiffness can be
changed by air pressure change, the natural frequencies of whole mechanical
system may be adjusted on desired value.
Keywords:
torsional vibration; pneumatic flexible shaft coupling; semi-active
vibroisolation
1. INTRODUCTION
Development
and application of pneumatic flexible shaft couplings are in the center of our
department research activities for a long time [1], [2]. These couplings are
able to change torsional stiffness by changing pressure in their flexible
elements – air bellows. Mechanical drives with periodically alternating load
torque (reciprocating engines and compressors) are prone to resonance,
pneumatic flexible shaft coupling are ideal device for protecting them from
excessive torsional vibration. This article deals with a problem of avoiding
resonance state on an example of diesel engine – electric generator mechanical
drive.
2. EXAMINED MECHANICAL SYSTEM
The selected mechanical system
consists of a 10-pole synchronous generator driven by
a 6-cylinder diesel engine. This mechanical system works on a constant
operating speed resulting from the required electric network frequency. It is
necessary to use a flexible shaft coupling with a proper torsional stiffness to
avoid resonance. The technical parameters of mechanical system are as follows
[3]:
Parameters of engine:
·
Turbocharged
diesel line engine type ČKD
6-27,5 A2L
·
Nominal
power by 600 RPM: PM = 515 kW
·
Mass
moment of inertia: IM = 137 kg.m2,
Parameters of generator:
·
Synchronous
generator type SIEMENS
1FC2 561-10
·
Input
power: PG = 492 kW
·
Operating
speed: no = 600 RPM
·
Number
of poles: 10
·
Mass
moment of inertia: IG = 61,0 kg.m2
Parameters of shaft coupling:
·
Pneumatic
flexible shaft coupling type 4–1/310–T–C
·
Dynamic
torsional stiffness:
N.m.rad-1 (1)
where pp0 kPa is air pressure in the coupling
·
Mass
moment of inertia of one hub: I1S = I2S =
29,86 kg.m2
Static and dynamic torsional
stiffness of coupling depends on air pressure pp0 kPa.
3. TORSIONAL VIBRATION ANALYSIS
This mechanical system can be
considered as a two-mass torsional oscillating mechanical system, where the
first mass J1 consists of masses JM and J1S,
and second mass consists of masses J2S and JG
(Fig. 1).
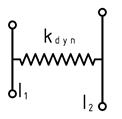
Fig. 1. Two mass torsional
oscillating mechanical system
The major harmonic component of load
torque for a six-cylinder four-stroke reciprocating engine is the third
harmonic component, the minor harmonics are the integer multiples of half
harmonic component. Minor harmonic may occur only by uneven cylinder operation.
The natural frequency of mechanical
system can be computed as:
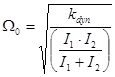rad.s-1 (2)
If resonance occurs during
operation, it can be determined from Campbell diagram (Fig. 2), where the natural frequencies in
RPM by different pressures (100, 200 ... 700 kPa) and harmonic frequencies of i-th
order are displayed. Where the frequency of torque harmonic is equal to natural frequency, a
resonance occurs.
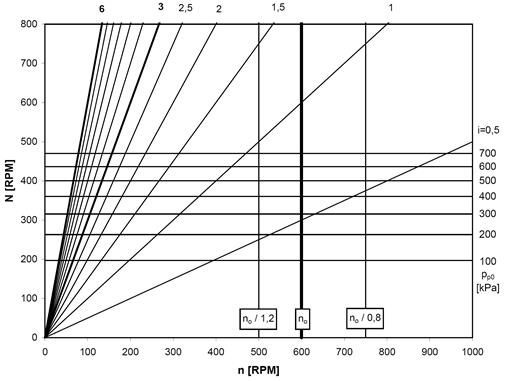
Fig. 2. Campbell diagram of examined mechanical
system
Speeds where resonances occur are
called critical speeds nkri. How critical speeds nkri
depend on pressure pp0 is displayed on fig. 3. By the
operating speed no = 600 RPM, only one resonance from 0,5-th
order may occur by pressure pp0 =264 kPa.
Resonance state is dangerous because
of increased torsional oscillation, which can damage the whole mechanical
system. According to several authors, the frequency ratio hi = w·i/W0 between i-th harmonics and natural frequency must satisfy the
condition: 
. On the
Campbell diagram (Fig. 1), no resonance should lie between no
/1,2 and no /0,8. The given mechanical
system can operate by pressures pp0=100, 500, 600 and 700 kPa.
By other pressures a resonance from 0,5-th order occurs near the
operating speed.
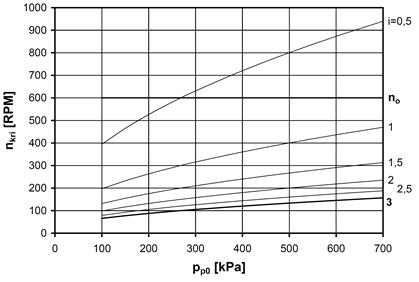
Fig. 3. Critical speeds, pressure graph
4. CONCLUSION
Based on
presented results, we can say that the natural frequency as well as critical
speeds of a torsional oscillating mechanical system can be tuned (changed) by
using a pneumatic flexible shaft coupling. Pneumatic flexible shaft couplings
are therefore considered not only as plain flexible shaft couplings, but
pneumatic tuners of torsional oscillation.
References
1. Homišin J. 2002. Nové typy pružných hriadeľových
spojok: vývoj, výskum, aplikácia. Košice: Vienala. ISBN 80-7099-834-2. [In
Slovak: New types of couplings flexible
shaft: development, research, application].
2. Kaššay P. 2008. „Optimalizácia torzne kmitajúcich
mechanických sústav metódou extremálnej regulácie”. PhD thesis. Košice:
Technical University of Košice. [In Slovak:
“Optimizing torsionally vibrating mechanical systems method Extremal Regulation”].
3. Kaššay P. 2014. „Modelovanie, analýza a optimalizácia torzne
kmitajúcich mechanických sústav”. Habilitation thesis, Košice: Technical
University of Košice. [In Slovak:
“Modeling, analysis and optimization torsionally vibrating mechanical systems”].
Acknowledgements: This paper was written in the
framework of Grant Project VEGA: „1/0688/12 – Research and application of
universal regulation system in order to master the source of mechanical
systems excitation”.
Received
23.10.2014; accepted in revised form 25.06.2015
Scientific Journal of Silesian University of
Technology. Series Transport is licensed under a Creative Commons
Attribution 4.0 International License