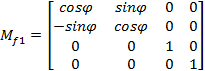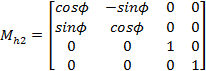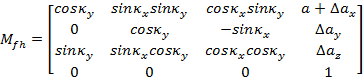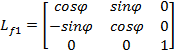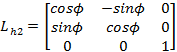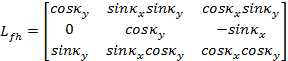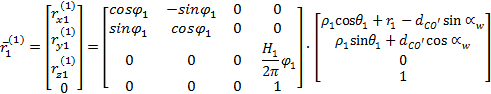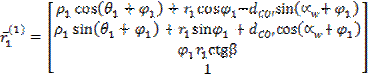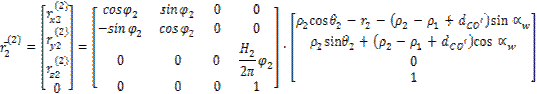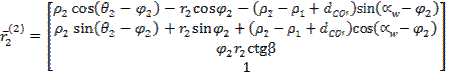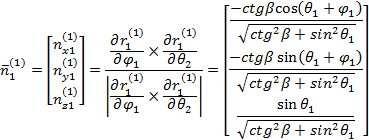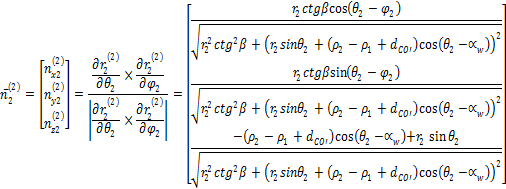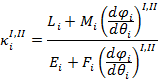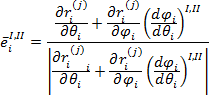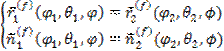Article citation info:

Batsch, M. Mathematical model of convexo-concave Novikov gear mesh. Scientific Journal of Silesian University of Technology. Series Transport. 2015, 89, 07-17. ISSN: 0209-3324.

DOI: 10.20858/sjsutst.2015.89.1.

 

Michał BATSCH[1]

 

 

 

MATHEMATICAL MODEL OF CONVEXO-CONCAVE NOVIKOV GEAR MESH

 

Summary. Article presents mathematical model of convexo-concave Novikov gear mesh. The parametric equations of teeth surface, units normal as well as main curvatures and main direction were obtained. Moreover the example of application of this model in tooth contact analysis was presented.

Keywords: mathematical model, Novikov convexo-concave gear, parametric equations, teeth surface

 

 

 

MATEMATYCZNY MODEL WKLĘSŁO-WYPUKŁEGO ZAZĘBIENIA TYPU NOWIKOWA

 

Streszczenie. W artykule przedstawiono matematyczny model zazębienia wklęsło-wypukłego typu Nowikowa. Wyznaczono parametryczne równania powierzchni bocznych zębów, wersory normalne do tych powierzchni oraz ich krzywizny i kierunki główne. Ponadto, zaprezentowano przykładowe zastosowanie tego modelu w analizie styku zębów.

Słowa kluczowe: model matematyczny, przekładna zębata Nowikova o kołowo-łukowym zarysie zębów, parametryczne równania, powierzchnia boczna zębów

1.      WPROWADZENIE

 

Przekładnie zębate typu Nowikowa odznaczają się większą nośnością powierzchniową od przekładni ewolwentowych. Zarys tego typu został zastosowany między innymi w przekładni głównej śmigłowca Westland Lynx [4, 5]. Pozwolił on na zmniejszenie liczby kół do 40% liczby kół o zarysach ewolwentowych stosowanych poprzednio [6].

W celu komputerowej analizy zazębienia należy dysponować jego modelem matematycznym. Model ten pozwala na symulację współpracy zębów przekładni, wyznaczenie błędu kinematycznego, drogi punktu styku na powierzchniach zębów, linii zazębienia czy śladu styku [1]. W niniejszym artykule zaprezentowano matematyczny model wklęsło-wypukłego zazębienia typu Nowikowa.

 

 

2.      matematyczny model zazębienia

 

     Analizowaną przekładnią jest walcowa przekładnia o stałych, równoległych osiach, składająca się z dwóch kół o uzębieniu Nowikowa. Zębnik posiadający zęby wypukłe współpracuje z kołem o zębach wklęsłych, co zostało pokazane na rysunku 1.

 

 

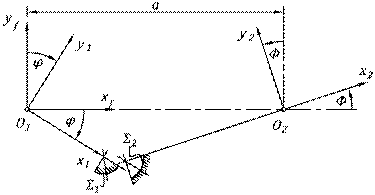
Rys. 1. Przyjęte układy współrzędnych

 

     Wprowadzono nieruchomy układ współrzędnych związany z korpusem przekładni xf, yf, zf oraz ruchome układy związane odpowiednio z zębnikiem oraz kołem x1, y1, z1 i x2, y2, z2. Zębnik obraca się wokół osi z1 przechodzącej przez punkt O1 o kąt  przeciwnie do kierunku trygonometrycznego. Koło natomiast obraca się wokół osi z2 przechodzącej przez punkt O2 o kąt , zgodnie z kierunkiem trygonometrycznym. Środki kół, a tym samym środki układów współrzędnych z nimi związanymi rozsunięte są na odległość a. Powierzchnia zęba zębnika  w układzie współrzędnych x1, y1, z1 opisana jest wektorem wodzącym . Podobnie powierzchnia zęba koła  w układzie współrzędnych x2, y2, z2 opisana jest wektorem wodzącym . Wobec powyższego zgodnie z rysunkiem 1 powierzchnie zębów zębnika i koła w nieruchomym układzie współrzędnych xf, yf, zf określone będą wzorami (1) i (2):

 

(1)

 

(2)

 

 

gdzie:

 – jednorodna macierz transformacji z układu 1 do f,

 – jednorodna macierz transformacji z układu 2 do f.

 

     Chcąc uwzględnić odchyłki położenia osi wynikające z błędów montażu, wykonania, odkształceń sprężystych wałów oraz łożysk, należy przesunąć układ współrzędnych związany z kołem wzdłuż osi xf, yf, zf o wielkości Δax Δay oraz Δaz, a następnie obrócić go względem stałych osi xf i yf o kąty odpowiednio  i . W tym celu wprowadzono dodatkowy pomocniczy układ współrzędnych xh, yh, zh pokazany na rysunku 2.

 

 

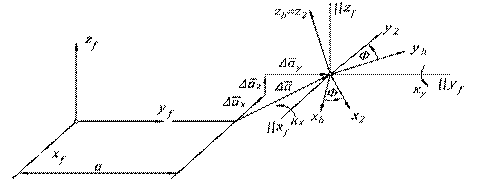
Rys. 2. Położenie i orientacja pomocniczego układu współrzędnych

 

     Po uwzględnieniu błędów koło będzie się obracać wokół nowej przesuniętej i przekoszonej osi zh=z2. Zgodnie z rysunkiem 2 macierz transformacji z układu 2 do f wyraża się za pomocą wzoru (3)

 

(3)

 

gdzie:

 – jednorodna macierz transformacji układu h do f,

 – jednorodna macierz transformacji układu 2 do h.

 

     Poszczególne macierze przyjmą postać:

 

(4)

 

(5)

 

(6)

 

     Ponadto, do opisu powierzchni należy stosować jednorodne reprezentacje wektorów.

     Przyjmując, że  i  są wersorami normalnymi do powierzchni zębów odpowiednio zębnika i koła w układach 1 i 2, wersory normalne w układzie f wyrażą się zależnościami:

 

(7)

 

(8)

 

gdzie:

 – macierz transformacji z układu 1 do f,

 – macierz transformacji z układu 2 do f.

 

     Ponadto, macierz transformacji z układu 2 do f wyraża się za pomocą wzoru

 

(9)

 

gdzie:

 – macierz transformacji układu h do f,

 – macierz transformacji układu 2 do h.

 

     Poszczególne macierze występujące we wzorach (7) i (8) otrzymuję się przez usunięcie ostatniego wiersza i ostatniej kolumny macierzy jednorodnych (4)-(6):

 

(10)

 

(11)

 

(12)

 

2.1. Parametryczne równania powierzchni bocznych zębów

 

     Rysunek 3 przedstawia przekrój czołowy współpracujących kół przekładni Nowikowa dla zerowych kątów obrotu kół.

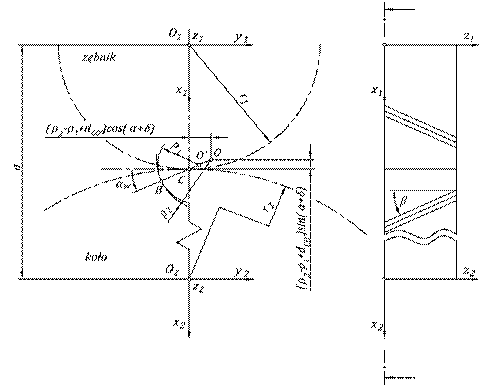
Rys. 3. Przekrój czołowy przekładni Nowikowa (αw – czołowy kąt przyporu, r1 – promień podziałowy zębnika, r2 – promień podziałowy koła, ρ1 – promień zarysu zęba wypukłego,
ρ2 – promień zarysu zęba wklęsłego, a – odległość osi kół, dCO’ – odległość pomiędzy centralnym punktem zazębienia C a środkiem zarysu zęba wypukłego O’, β – kąt pochylenia linii zęba na średnicy podziałowej)

 

     Zębnik o zębach wypukłych i promieniu podziałowym r1 współpracuje z kołem o zębach wklęsłych i promieniu podziałowym r2. Punkt styczności zarysów zębów B określony jest przez kąt αw. Punkt O’ jest środkiem zarysu zęba wypukłego o promieniu ρ1, natomiast punkt O jest środkiem zarysu zęba wklęsłego o promieniu ρ2. Punkt C jest centralnym punktem zazębienia, będącym punktem styku okręgów podziałowych.

     Parametryczne równanie powierzchni bocznej zęba wypukłego utworzono przez jednoczesny obrót wokół osi z1 o kąt  zgodny z kierunkiem trygonometrycznym oraz translację wzdłuż dodatniego kierunku osi z1 o  łuku okręgu. Macierzowy zapis przekształcenia wyraża się za pomocą wzoru (13)

 

(13)

 

gdzie:

 − parametr linii śrubowej,

 − parametr okręgu,

H1 – skok linii śrubowej określony zależnością (14)

 

(14)

 

gdzie

β to kąt pochylenia linii zęba na walcu podziałowym.

 

     Ostatecznie wykorzystując zależności (13) oraz (14) wektor wodzący powierzchni bocznej zęba w układzie x1, y1, z1 wyraża się za pomocą wzoru (15)

 

(15)

 

     Parametryczne równanie powierzchni bocznej zęba koła utworzono w sposób analogiczny, z tą różnicą że obrót łuku okręgu nastąpił wokół osi z2 o kąt  przeciwny do kierunku trygonometrycznego oraz translacja odbyła się wzdłuż dodatniego kierunku osi z2 o  .

     Macierzowy zapis przekształcenia wyraża się za pomocą wzoru (16)

 

(16)

 

gdzie:

 − parametr linii śrubowej,

− parametr okręgu,

H2 – skok linii śrubowej określony zależnością (17)

 

(17)

 

     Ostatecznie wykorzystując zależności (16) oraz (17) wektor wodzący powierzchni bocznej zęba w układzie x2, y2, z2 wyraża za pomocą wzoru (18)

 

(18)

 

2.2. Wersory normalne do powierzchni

 

     Wersor normalny do powierzchni bocznej zęba zębnika oraz koła w układzie współrzędnych odpowiednio 1 i 2 wyrażają się za pomocą wzorów (19) i (20)

 

(19)

 

(20)

 

     W artykułach [2, 3], w których opisywano lokalną geometrię zębów, wersory normalne różnią się w zapisie od prezentowanych. W szczególności wersor normalny do powierzchni zęba koła przyjmuje znacznie prostszą postać. Wynika to z uproszczenia geometrii zęba koła przez Autorów, która została uzyskana w wyniku translacji punktów łuku okręgu o wektor o współrzędnych będących współrzędnymi kolejnych punktów linii śrubowej. Aby móc wykorzystać wersory normalne w globalnej analizie styku zębów, zdecydowano się na dokładne odwzorowanie geometrii zębów.

 

2.3. Krzywizny i kierunki główne powierzchni

 

     Kierunki główne powierzchni  zadanej parametrycznie określone są jako rozwiązania równania kwadratowego (21)

 

(21)

 

gdzie:

 

(22)

 

są elementami pierwszej formy kwadratowej powierzchni,

 

(23)

są elementami drugiej formy kwadratowej powierzchni, – wersor normalny.

     Indeks i=1,2 w powyższych wzorach odnosi się do powierzchni bocznej zęba wypukłego oraz wklęsłego, natomiast indeks j=1,2,f odnosi się do układu współrzędnych.

     Równanie (21), przy założeniu że jego wyróżnik jest większy od zera, posiada dwa rozwiązania, określające pierwszy oraz drugi kierunek główny powierzchni wyrażone w postaci (24)

 

(24)

 

     Krzywizny główne powierzchni określone są za pomocą wzoru (25)

 

(25)

 

     Kierunki główne natomiast określone są wektorami jednostkowymi (26)

 

(26)

 

     Ponadto główne promienie krzywizny wyrażają się zależnością (27)

 

(27)

 

 

3.    Analiza styku zębów

 

     Kompletna analiza styku zębów, oprócz wyznaczenia obszaru styku przekładni, obejmuje również wyznaczenie linii styku oraz zależności pomiędzy kątami obrotu kół przekładni (błąd kinematyczny, stałość przełożenia) [1]. W tym celu przyjmuje się, że wektory wodzące powierzchni bocznych zębów w nieruchomym układzie współrzędnych muszą być sobie równe, co wyraża warunek (28)

 

(28)

 

     Jego spełnienie zapewnia, że powierzchnie boczne zębów będą miały punkt wspólny. Kolejnym warunkiem jest równość wersorów normalnych, która zapewni ciągłą styczność powierzchni (29)

 

(29)

 

 

 

 

 

     Równania (28) i (29) można zapisać jako układ (30)

 

(30)

 

     Zadaniem analizy styku jest wyznaczenie z układu (30) związków pomiędzy parametrami  a kątem obrotu zębnika . Można to zrealizować rozwiązując powyższy układ numerycznie dla kolejnych dyskretnych wartości kąta obrotu zębnika . Tym sposobem otrzymuje się funkcje

 

.

(31)

 

     Następnie po wprowadzeniu funkcji (31) do wzorów (15) i (16) otrzymuje się drogę punktu styku na powierzchni bocznej odpowiednio zębnika  oraz koła . Podobnie po wprowadzeniu zależności (31) do wzorów (1) i (2) uzyskuje się linie styku , .

     Na rysunku 4 przedstawiono graficznie wynik rozwiązania układu równań (30) dla przykładowej przekładni Nowikowa. W przypadku przekładni idealnej, w której nie uwzględniono błędów położenia osi kół, linia styku jest linią prostą równoległą do osi z, przechodzącą przez punkt styku B. Droga punktu styku na powierzchni zębów kół przekładni jest natomiast fragmentem linii śrubowej leżącej na linii współrzędnej  dla zębnika oraz na linii współrzędnej  dla koła.

     Na rysunku 4a) przedstawiono wyniki analizy styku zębów przekładni Nowikowa z nierównoległością osi . W wyniku błędu nierównoległości osi droga punktu styku na powierzchniach zębów podczas ruchu punktu styku od wejścia w zazębienie do połowy szerokości wieńca odchyla się w kierunku głowy zęba zębnika i stopy zęba koła. Sytuacja ta jest odwrotna w przypadku ruchu punktu styku od połowy szerokości wieńca aż do wyjścia z zazębienia, gdzie droga punktu styku odchyla się w kierunku stopy zęba zębnika i głowy zęba koła. Ponadto, drogi punktu styku na powierzchniach zębów nie są już liniami współrzędnych  dla zębnika oraz  dla koła. Fakt ten może powodować zmianę wielkości nacisków i prędkości poślizgu, które to w przypadku przekładni bezodchyłkowej są stałe.

     W wyniku symulacji przeprowadzonych dla przekładni z odchyłką przekoszenia osi stwierdzono, że nie wywołuje ona istotnych zmian w ruchu punktu styku. Na rysunku 4b) przedstawiono wyniki analizy styku zębów dla odchyłki położenia osi . W wyniku uwzględnienia błędu rozstawienia osi rzeczywisty kąt przyporu maleje, co objawia się przesunięciem drogi punktu styku na powierzchni zębów ku stopie zęba zębnika oraz ku głowie zęba koła. Linie te nadal pozostają liniami współrzędnych  dla zębnika oraz  dla koła.

 

 

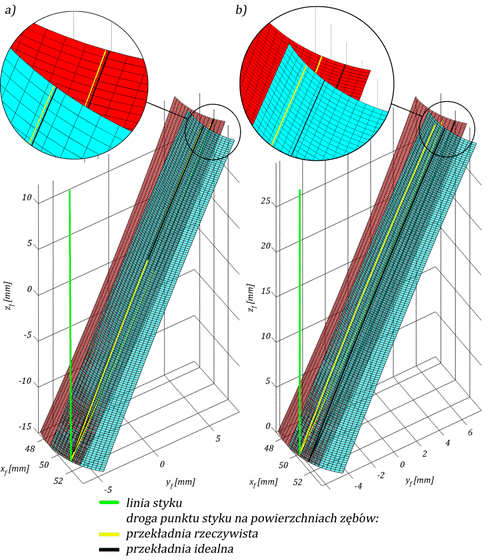
Rys. 4. Wynik analizy styku zębów przekładni Nowikowa: a) przekładnia z błędem przekoszenia osi, b) przekładnia z błędem rozstawienia osi

 

 

4.    Wnioski i podsumowanie

 

     Opracowany model matematyczny wklęsło-wypukłego zazębienia Nowikowa pozwala na komputerową analizę styku zębów. W wyniku zastosowania tego modelu wyznaczono linie styku i drogi punktu styku na powierzchniach bocznych zębów zarówno dla przekładni z odchyłką położenia osi, jak też dla przekładni idealnej. Ponadto model ten może zostać wykorzystany w przypadku wyznaczania śladu styku przekładni zarówno w metodzie, w której odległość mierzona jest wzdłuż wersora normalnego, jak też wzdłuż normalnej do płaszczyzny stycznej. Co więcej, wyprowadzone parametryczne równania powierzchni bocznych zębów mogą posłużyć do wyznaczania sprzężonych zarysów narzędzi do obróbki tego typu uzębień.


     Analizy wykorzystujące zaprezentowany model zazębienia pokazały, że błąd rozstawienia osi kół znacząco wpływa na obniżenie rzeczywistego kąta przyporu i przesunięcie punktu styku ku stopie zęba zębnika. Może to skutkować obniżeniem naprężeń stykowych, pod warunkiem że nie wystąpi krawędziowanie śladu styku. Również błąd przekoszenia osi kół przekładni powoduje stopniowe odchylanie się drogi punktu styku w kierunku głowy bądź stopy zęba zębnika.

 

 

5.    Podziękowania

 

     Badania realizowane w ramach Projektu "Nowoczesne technologie materiałowe stosowane w przemyśle lotniczym", Nr POIG.01.01.02-00-015/08-00 w Programie Operacyjnym Innowacyjna Gospodarka (PO IG). Projekt współfinansowany przez Unię Europejską ze środków Europejskiego Funduszu Rozwoju Regionalnego.

 

 

References

 

1.      Litvin F.L., A. Fuentes A. 2004. Gear Geometry and Applied Theory. Cambridge: Cambridge University Press.

2.      Markowski T., M. Batsch. 2014. „Analityczno-numeryczne metody wyznaczania obszaru styku przekładni wklęsło-wypukłych Nowikowa”. Scientific Journal of Silesian University of Technology. Series Transport 82: 155-165. [In Polish: „Analytical and numerical methods of determining the contact area convex-concave gear Novikov”].

3.      Markowski T., M. Batsch. 2013. “Analiza parametrów styku przekładni zębatych o kołowo-łukowym zarysie zębów typu Nowikowa”. Przegląd mechaniczny 7-8: 50-53. [In Polish: “Analysis of the parameters of contact gears on the circular-arc tooth outline the type of Novikov”].

4.      Dyson A., H.P. Evans, W. Snidle. 1989. “Wildhaber-Novikov cicrular-arc gears: some properties of relevance to their design”. Proceedings of The Royal Society A Mathematical Physical and Engineering Sciences 425(1825): 341-363.

5.      Dyson A., H.P. Evans, W. Snidle. 1986. “Wildhaber-Novikov circular arc gears: Geometry and Kinematics”. Proceedings of The Royal Society A Mathematical Physical and Engineering Sciences 403(1825): 313-349.

6.      Ellis D.V. 1980. “The Westland Lynx”. The RUSI Journal 125(4): 70-73.

 

 

Received 11.05.2015; accepted in revised form 21.09.2015

 

 

Scientific Journal of Silesian University of Technology. Series Transport is licensed under a Creative Commons Attribution 4.0 International License


[1] Faculty of Mechanical Engineering and Aeronautics, Rzeszow University of Technology, al. Powstańców Warszawy 8, 35-959 Rzeszów, Poland. E-mail: mbatsch@prz.edu.pl