Article citation information:

Doğan, E. Performance analysis of LSTM model with multi-step ahead strategies for
a short-term traffic flow prediction. Scientific Journal of Silesian University of Technology. Series Transport. 2021, 111, 15-31. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2021.111.2.

 

 

Erdem DOĞAN[1]

 

 

 

PERFORMANCE ANALYSIS OF LSTM MODEL WITH MULTI-STEP AHEAD STRATEGIES FOR A SHORT-TERM TRAFFIC FLOW PREDICTION

 

Summary. In this study, the effect of direct and recursive multi-step forecasting strategies on the short-term traffic flow forecast performance of the Long Short-Term Memory (LSTM) model is investigated. To increase the reliability of the results, analyses are carried out with various traffic flow data sets. In addition, databases are clustered using the k-means++ algorithm to reduce the number of experiments. Analyses are performed for different time periods. Thus, the contribution of strategies to LSTM was examined in detail. The results of the recursive based strategy performances are not satisfactory. However, different versions of the direct strategy performed better at different time periods. This research makes an important contribution to clarifying the compatibility of LSTM and forecasting strategies. Thus, more efficient traffic flow prediction models will be developed and systems such as Intelligent Transportation System (ITS) will work more efficiently. A practical implication for researchers that forecasting strategies should be selected based on time periods.

Keywords: traffic flow, LSTM, short-term prediction, multi-step ahead strategies

 

1. INTRODUCTION

 

The significant increase in vehicle numbers and travel demand raises traffic density on roads to critical levels. Proper management of traffic flow can reduce this density. Today, this task is carried out with smart systems operating under the Intelligent Transportation System (ITS) and, these systems need information about future traffic conditions. However, short-term traffic forecast is a challenging task of modern ITS. Therefore, significant improvements are needed in developing a high-performance traffic flow prediction model or improving existing models. Existing models can be developed by optimising their parameters or using different forecasting strategies.

The first study for the short-term traffic flow prediction task was published in 1979 [1]. In the following years, parametric and time series models were used for the prediction task [2-10]. The emergence of artificial intelligence techniques such as Artificial Neural Networks (ANNs), Fuzzy Logic, etc. accelerated the development of sophisticated short-term traffic prediction models [11-14]. However, the exploding/vanishing gradient problem of ANNs prevented the development of more advanced models in the time series. Researchers overcome this problem with the Long Short-Term Memory (LSTM) method developed in 1997 [15]. After this study, prediction models based on the LSTM approach emerged.

LSTM is used in various fields, especially in time series. Interestingly, LSTM was not utilised for traffic flow prediction task until a study in 2016 [16]. Most studies on traffic flow prediction in recent years aimed at developing a hybrid model with LSTM or compare LSTM with other approaches. The LSTM model was improved with the k-nearest neighbour (KNN) and compared with some state-of-art methods [17]. The developed model results were slightly better than the standard LSTM model and significantly better than other methods. Another study combined LSTM with an attention mechanism that detects previous time steps that have a high impact on the current time step [18]. An LSTM model using temporary information (T-LSTM) was developed [19]. Further, in the same study, T-LSTM errors were compared with support vector machine, ARIMA and gated recurrent unit, etc. approaches. The authors posit that the proposed technique increases LSTM's prediction accuracy. A hybrid prediction model was developed using the graph convolutional network and LSTM [20]. This hybrid model reduced errors slightly compared to the traditional LSTM model.

LSTM's success in sequential data has motivated researchers to do more study on the subject. Thus, LSTM was used for traffic flow prediction tasks in a substantial number of studies. Generally, in these studies, LSTM's traffic flow prediction performance was compared with other methods, or its structure was updated to improve its performance, or a hybrid model was developed using LSTM and other popular approaches. However, in these studies, performance analysis of using a multi-step forecasting strategy with LSTM for traffic flow prediction was not performed. Therefore, there is an important research gap in this field. To close this important gap, this study investigated which multi-step forecasting strategy works efficiently with an LSTM model in the traffic flow prediction task. Thus, this study contributes to developing high accuracy LSTM models for the traffic flow prediction task.

Three primary strategies and some of their combinations were proposed in the literature for multi-step forecasting task. These primary strategies are direct strategy based on developing a new model for each step. A Recursive strategy that develops a single model and uses the previous forecast value for each step in each step. Finally, a Multi-Input Multi-Output (MIMO) strategy that developed only one model with the historical data set and predicts the forecast horizon at once. Additionally, DirRec, the combination of the direct and recursive strategy, and DirMo, the combination of the direct and MIMO strategy [21]. Many studies in different fields have been achieved with multi-step forecasting strategies [22-27]. However, most of the study results are inconsistent about the proper strategy [21]. Furthermore, the fact that different prediction problems have atypical features makes it difficult to solve this inconsistency. Therefore, the issue of which strategy is good for which problem is still completely unresolved. The investigation using different forecasting strategies with LSTM in terms of the traffic flow prediction problem, and the analysis of these results will contribute to the solution of this inconsistency.

A few studies in the literature examined the traffic flow prediction with a multi-step ahead strategy. Adaptive Kalman filtering theory-based prediction models were proposed and compared with the Gaussian Maximum likelihood and Constant and Heuristics Predictor approaches [28]. The models were tested for forecasting horizons from 15 to 45 min. The forecast horizons examined are short and only proportional performance criteria such as MAPE and APE were utilised. Therefore, the long forecast horizon performances of the proposed models have not been revealed. In addition, a one-way performance comparison is another disadvantage of the study. A study using the spectral analysis and statistical volatility model proposed a hybrid model. A one-step to ten-step ahead forecasts of the models utilised were compared [29]. The proposed hybrid model performance was compared with the ARIMA-GARCH model, and the hybrid model error was reported to be fewer. Multi-step ahead strategies and gradient boosting regression tree were used for the traffic speed prediction task [30]. Support vector regression was used as the benchmark model and the researchers stated that the proposed model was better. They similarly concluded that the DirRec strategy gave satisfactory results for the short forecast horizon.

This article is divided into four sections. The introduction covers the aim of this study and a literature review on the subject. In the methodology section, the LSTM approach, the k-means++ algorithm, multi-step ahead forecasting strategies and the criteria used in measuring errors are introduced. This is followed by the section where the experimental results and the results are discussed. Finally, the recommendations that emerged from this study and plans for further studies are included in the conclusion.

 

 

2. METHODOLOGY

 

2.1. K-means++ and dropping similar datasets

 

Using various large datasets in a study increases the reliability of the analysis results. However, analysis with many similar data sets increases the cost of the analysis and its effect on the results is limited. Excessive analysis can be avoided by dropping similar datasets. Many traffic flow data sets were collected for this study. Therefore, the procedure to reduce the number of datasets was applied. To extract similar datasets, datasets were clustered according to their similarities. This process was performed with the k-means++ algorithm according to the statistical properties of the datasets.

The k-means is an unsupervised widely-used clustering algorithm that clusters data sets according to their similarities [31]. The k-means++ is an advanced version of the k-means algorithm and improves the quality of the final solution [32]. Therefore, k-means++ was preferred rather than the conventional k-means to cluster datasets in this study. However, the traffic flow datasets are time-dependent and contain plenty number of data samples. For k-means++ to be able to cluster more effectively, the properties of this time series should be expressed with fewer features. Hence, traffic flow data are expressed with common statistical estimators.

Let denote the sth traffic flow dataset, where M is the number of observations, . Then, the estimators are arithmetic mean , standard deviation (, maximum (max ) and minimum (min) values of the dataset. Thus, the estimator’s vector in Equation 1 expresses a data set using four statistical estimators of the dataset.

 

                                         (1)

 

The  vectors are created for each traffic data set and aggregated in set E. The E is the set of vectors and can be expressed as , where N is the total number of datasets. Thus, the datasets are arranged to be clustered by k-means++.

The k-mean++ algorithm searches for centroids with a heuristic approach. First, k-mean++ randomly selects a random observation and defines it as a first centroid . Then, it calculates the Euler distances (d2) of each observation to the . The new centroid is calculated with a probability ratio based on d2. The algorithm repeats this process until it reaches the total number of centroid (P). On the other hand, determining the appropriate P, that is, number of clusters increases the reliability of the analysis. Gap statistics used in this study is recommended as a superior method for estimating cluster numbers and it forecasts the optimum P using the within-cluster sum of squares [33]. Finally, each  is assigned to a centroid with probability computation.

To avoid costly analysis, a certain upper limit (Ng) was determined for the number of  in the clusters. Thereafter, Ng random elements were selected in each cluster and this set of elements was named as the next generation of that cluster. Thus, the number of members in each cluster decreased. This step provided the advantage of faster analysis.

 

2.2. LSTM model structure

 

Recurrent Neural Network (RNN) is the previous version of LSTM [34]. RNN's deficient performance in solving the long-term dependencies problem is the motivation for the development of LSTM. LSTM is a gradient-based method and consists of connecting sequential LSTM units. LSTM units include structures such as input gate (i), output gate (o), and forget gate (f) as illustrated in Figure 1 [15]. LSTM overcomes the problem of long-term dependencies using these gates.

The connections between the successive LSTM units and these are given in Figure 1. Let time be t. Thus, the inputs of the LSTM unit at t are: The input vector (xt), the cell state of the previous LSTM unit (Ct-1) and the hidden state of the previous LSTM unit (ht-1). The unit has two exits. These are: cell state (Ct) and hidden state (ht) at t.

The first step to calculate the outputs of an LSTM unit ate time t is the forget gate operation and it is calculated by Equation 2. Let σ be the sigmoid function, W(f,i,c,o) be the network parameters matrix, b(f,i,c,o) be the bias matrices and ⊙ denotes the product operation.

 

 

The next step is to identify the new information to be stored in the cell state. Therefore, the new candidate () and the input gate it are calculated using Equation 3-4.

 

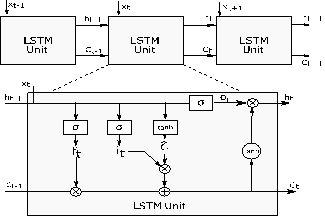
Fig. 1. Long short-term memory network unit

 

 

 

After these steps, Ct-1 is updated by using the ft, it and in Equation 5.

 

 

The output gate (ot) is the process that determines the parts of the cell state that will be in the output and can be written as:

 

 

The other output of the LSTM unit, ht, is calculated using Equation 7.

 

 

2.3. Multi-step forecasting strategies

 

Let H be the prediction horizon and M be the number of observations. Thus, multi-step prediction is the developing of a model using a series composed of M observation [x1, ..., xM], and estimating the next H values [xM+1, ..., xM+H] of the series with the developed model. This section presents three different multi-step forecasting strategies for forecasting traffic flow.

 

2.3.1.      Direct strategy 1

 

Direct strategy-1 (Dir-1) updates the model at every step. Thus, the prediction speed of the model increases. However, as the size of the forecasting horizon increases, forecast error increment probability Dir-1 may increase.

Assume that an untrained LSTM model is . First, the  is trained with  and becomes a trained LSTM model (). Subsequently, the steps in the forecasting horizon are predicted using Equation 8.

 

where, t is the current time,  is the current time traffic flow and  is the one- step ahead prediction from t.

 

2.3.2.      Direct strategy 2

 

Direct strategy-2 (Dir-2) is based on the principle of updating the model with the current observation at each step and the prediction of the next step with the updated model. Let Lh be the untrained LSTM model, where , where H is the forecasting horizon. In the first step, Lh is trained with the training set   and becomes . Thus, the prediction value for h = 1 will be written as  . Other horizon predictions are calculated by Equation 9 while .

 

 

Direct strategy-1 (Dir-1) updates the model at every step. Thus, the prediction speed of the model increases. However, as the size of the forecasting horizon increases, forecast error increment probability Dir-1 may increase.

Assume that the untrained LSTM model is . First, the  is trained with  and becomes a trained LSTM model (). Subsequently, the steps in the forecasting horizon are predicted by using Equation 10.

 

 

DS requires the updating of every step of the model state, that is, the LSTM network state is updated with  or  in each step. This approach may result in accurate forecasts. On the other hand, training the model with new values in each step is an expensive approach in terms of calculation time. Let Tso be the computational time. Thus, DS requires a computational time of H x Tso for H steps [35]. Although DS requires a large computation time, it has been used with a variety of learning and optimisation algorithms. For example, neural networks [24, 36] and extreme gradient boosting [27], whale optimisation algorithm [22], gradient boosting regression tree [30, 37], etc.

 

2.3.3.      Direct-Recursive strategy

 

Direct-Recursive strategy (DirRec) is based on the combination of direct and recursive strategies. First, a model is created with available observation data in the direct and recursive strategy. Next, predictions are made one step ahead. In each step, the previous model prediction is used in the model to make predictions of future values. Similar to Dir-2,  is trained using the Tr and is formed after training.  At each step, the LSTM network state is updated with , i.e., . Equation 11 presents the inputs used in the prediction in h=1 and h>1 stage.

 

 

The plurality of noise in the dataset can increase model errors in prediction jobs with large H. Therefore, keeping the forecast horizon short may be to the advantage of this method. The number of studies using DirRec is limited [38-40], thus, there is potential for further studies.

 

2.4. Error criteria and forecast horizon periods

 

The errors of the strategies used in the dataset were evaluated with three performance criteria. These are Mean Absolute Percentage Error (MAPE), Mean Squared Error (MSE) and Root Mean Squared Error (RMSE), which are frequently used to analyse model error. The equations of the criteria are in Equations 11-13.

 

 

 

 

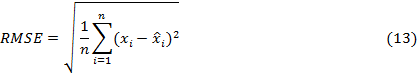
To determine the overall error trend of multiple data sets, the average errors of all data sets were calculated for the error criteria by dividing Equations 11-113 to N. Where,  is the actual traffic flow, is the forecasting value, N is the number of datasets. The RMSE difference between the errors of Dir-1 and Dir-2 strategies was calculated using Equation 14.

 

 

LSTM errors were calculated separately for three predefined time periods, to better understand the behaviour of the strategies within the forecast horizon. Let xt be the current time traffic flow, thus, traffic flow set for Period 1 can be written as  where, HP1 is forecasting horizon of the P1. Furthermore, the traffic flow sets for Period 2 and Period 3 can be written as,   and , respectively.

 

 

3.    EXPERIMENTAL SETUP

 

This section concerns data set and model training pre-treatments. First, information was given about the analysed datasets. Then, clustering of data sets with the k-means algorithm was discussed. Hyperparameters used in the training step of the LSTM model are given.

 

3.1. Data and data set clustering

 

A large number of data sets were used to analyse the result of using LSTM with different forecasting strategies. This dataset requirement was met from the PeMS database [41]. The PeMS database consists of information transmitted from detectors located on highways in the state of California. Researchers can easily obtain raw traffic data or processed data.

Care was taken to ensure that the datasets used in this study were up-to-date, statistically different.  In addition, months in which the demand for travel increased were considered for better interpretation of model errors. For this reason, k-means++ analyses were made for 472 main lane data sets obtained from May to August 2018. Lane traffic with different features, for example, on-ramp/off-ramp, conventional highway lane, etc., were not used for the analysis. Because different traffic patterns of these roads may decrease the model performance.

Development and training of LSTM models for each data set consume considerable computation time. To reduce the computation time, statistically similar datasets were clustered with the k-means++ algorithm [32] and 20 datasets were randomly selected from these clusters for further analysis. k-means++ can avoid some weak clusters found by the standard k-mean algorithm. In addition, k-means ++ is frequently used for clustering in studies in many different fields [42-45]. Hence, k-means++ was preferred to cluster the datasets.

 

 

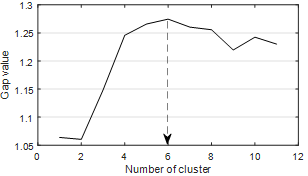
Fig. 2. Gap values for different number of clusters

 

The performance of a clustering algorithm increases due to determining the optimal number of clusters for the problem. Therefore, various methods, for example,  Davies-Bouldin, Calinski-Harabasz, Gap Statistic, Silhouettes [46-49] have been developed to select the optimum number of clusters. The gap statistic method can be used with any distance metric and is defined even for only one set [50], so it was preferred for this study. Gap statistic calculates a variable named gap value for different cluster numbers, and the number of clusters with the largest gap value is the best solution. The best cluster number for this study is “6” and this number was determined from Figure 2, which shows the result of gap statistics.

After determining the best number of clusters, 482 data sets were clustered into 6 clusters using k-means++. Thus, similar data sets were collected in the same cluster. Then, 20 data sets from each set were randomly selected. The scattering of all and selected datasets according to average and standard deviation values is given in Figure 3. The datasets of each cluster are coloured in Figure 4 for better visualisation. This step is expected to have affected the study result. However, this effect is extremely low since it contains samples from all clusters. However, the modelling and analysis speeds were increased significantly.

 

 

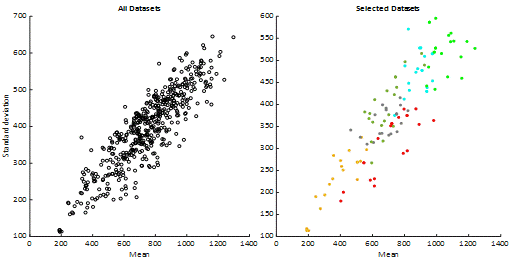
Fig. 3. Mean and standard deviation scatter plots for all and selected data sets

 

Tab. 1.

Average descriptive statistics of the clusters

 

Cluster

Part

Mean

Std

Min

25%

50%

75%

Max

C1

Train

885

475

93

410

990

1275

1774

Test

902

478

117

437

1037

1293

1723

C2

Train

704

310

134

434

740

899

1950

Test

695

290

224

436

754

895

1378

C3

Train

371

224

23

157

392

534

1006

Test

383

224

48

171

406

539

962

C4

Train

682

359

84

331

760

961

1401

Test

705

369

99

350

813

991

1352

C5

Train

690

396

31

307

741

996

1656

Test

708

412

62

302

777

1027

1553

C6

Train

1044

522

135

499

1199

1497

1931

Test

1070

517

206

544

1263

1509

1848

 

To demonstrate that the data sets used are multifarious, the average statistical properties of the data sets in the clusters are summarised in Table 1. For the training stage of the LSTM models, 90% of the observations in the data sets were reserved. The remaining 10% was used during the testing phase. In Table 1, the statistical characteristics of these observations are given separately. Thus, patterns can be discussed between LSTM model errors and these statistical properties.

 

3.2. LSTM model and parameters

 

The LSTM and other layers in the deep learning network architecture used in this study are illustrated in Figure 4. The network consists of input and output layers and four other hidden layers. The LSTM layer is located after the input layer.  The network output value is calculated using a regression layer.

 

 

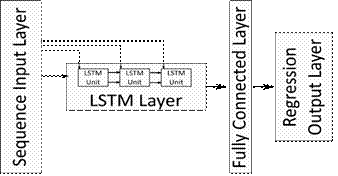
Fig. 4. Deep learning network architecture and LSTM layer

 

Determining the proper network structure and parameters affects the predictive performance of the network. In particular, the number of LSTM units significantly affects performance. Consequently, experiments were carried out to determine the proper number of units for each data set. In each experiment, models were developed by trying the number of units between 5 and 250. Afterwards, the models with the lowest prediction error were determined for comparison. Adam optimisation algorithm, widely accepted for deep learning applications, was used [51]. The maximum number of epochs is set to 250. The gradient threshold value was set to "1" in LSTM training. The initial learning rate was determined as 0.005 and the learning rate value was decreased by multiplying the learning rate by 0.2 in every 125 years. Before starting the model training, the data set was standardised for a better fit with zero mean and unit variance. Fully connected layer output size is set to 50 and fixed for all trials

 

 

4.    COMPARISON OF STRATEGY PREDICTION ERRORS

 

Traffic flow prediction errors of LSTM models using different prediction strategies are statistically analysed in this section. In addition, the prediction errors of the models for different time periods determined for this study were compared. Thus, the impact of a strategy on errors was more clearly analysed for different forecast horizons.

The errors of the strategy predictions are summarised in Table 2 according to the error criteria and periods described in Section 2.4. The lowest and highest outliers were removed from the dataset prediction errors and analyses were performed for the remaining values. The DirRec strategy errors are significantly higher than others. For example, DirRec all MAPE and RMSE are about 4 times and all MSE is about 9 times more than other strategy criteria. This result leads to the conclusion that no apparent advantage exists in utilising the DirRec strategy for traffic flow prediction. Therefore, the DirRec strategy was not discussed further.

The "All" line of Table 2 states that the errors of Dir-1 and Dir-2 strategies are close to each other, however, on average, the performance of Dir-2 is a little more advanced. The period errors in the table clearly reveal the superiority of Dir-2 for P1 over Dir-1. However, this advantage is limited for P2 and P3. In fact, Dir-1's MAPE value for P3 is lower than Dir-2 MAPE. This result suggests that the Dir-1 might have some advantages in predicting the lower traffic flows in distant forecasting horizon.

To visualise the results of Table 2, the actual traffic flow and strategy predictions for station No: 312865 are shown in Figure 5 for the P1 period. The DirRec predictions are less accurate than other strategies, and they can be easily determined from the shape. In addition, Figure 5 confirmed that the other two strategies have close predictions.

Tab. 2.

Mean errors of forecasting strategies for periods

 

Forecasting

Periods

Dir-1

Dir-2

DirRec

P1 ()

11.11

70.6

5655

8.13

50.5

2987

26.69

156.8

30271

P2 ()

8.62

53.5

3268

8.27

52.6

3220

29.40

149.4

27385

P3 ()

8.91

59.2

3886

9.07

58.1

3773

29.73

178.1

35758

All

9.31

61.1

4269

9.28

53.8

3327

43.33

161.4

31138

 

The ΔRMSE is calculated by Equation 15 and the distributions of ΔRMSE are given in Figure 6. Due to the poor results, DirRec is not considered here. The negative and the positive ΔRMSE indicate that Dir-2 and Dir-1 have a low error, respectively. The ΔRMSE is positive in 9 out of 120 datasets in P1. Therefore, Dir-1 has lower RMSE for these 9 datasets. Dir-2 has a lower RMSE in the remaining 111 datasets. 

 

 

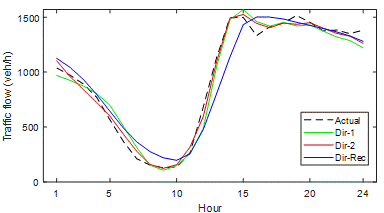
Fig. 5. Comparison of multi-step ahead strategy predictions for P1 (Station No: 312865)

 

Conclusively, using Dir-2 in the short prediction horizon, that is, P1, provides an important advantage. On the other hand, P2's ΔRMSE number greater than zero and less than zero is close to each other. This proximity likewise occurs for P3 and becomes more concentrated around 0. Consequently, the use of Dir-2 is advantageous for P1, and in other periods, the two strategies have no significant superiority over each other.

 

 

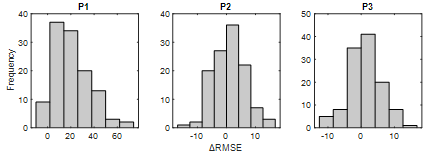
Fig. 6. ΔRMSE distributions of Dir-1 and Dir-2 strategies for time periods

 

The errors in low value observations have a high effect on MAPE. Therefore, it is suitable for analysing performances in low traffic flows. In Figure 7, MAPE values of Dir-1 and Dir-2 are presented using box diagrams. In P1, Dir-1's highest MAPE is around 23% and lowest MAPE around 5%. On the other hand, when outliers are not considered, Dir-2 has MAPEs in the range of 15 to 3%. It can also be seen from the box plot that 50% of Dir-1 MAPE measurements are between 7 and 14%. However, 50% of Dir-2 MAPE measurements are between 6 and 9%. Hence, Dir-2 predicts low traffic flows more successfully than Dir-1 in P1.

 

 

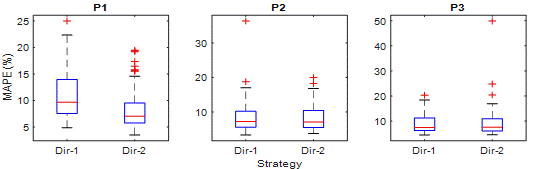
Fig. 7. MAPE boxplots of Dir-1 and Dir-2 for time periods

 

In P2, the MAPE values of the two strategies are close to each other. However, one of the outliers of Dir-1 has 35% MAPE. Therefore, MAPE value of Dir-1 in Table 2 is higher than Dir-2. Box and box moustaches in P3 indicate that Dir-2 is slightly better than Dir-1 as well, however, one of the outliers of Dir-2 has a MAPE value of 50%. Therefore, in Table 2, it turns out that Dir-1 is better in terms of average MAPE. However, Dir-2 shows better performance for the majority number of the data sets.

 

 

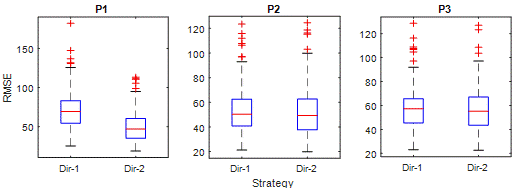
Fig. 8. RMSE boxplots of Dir-1 and Dir-2 for time periods

 

Figure 8 shows the RMSE of strategies. The RMSE criterion punishes relatively large errors more. Therefore, it is a suitable criterion for comparing predictions that strategies have high errors. The superiority of Dir-2 in P1 is clear in the RMSE criterion. However, there are interesting results for other periods. Although the RMSE distribution in P2 is close, the upper moustache of the Dir-1 has an RMSE value of around 90, while the Dir-2s are around 100, meaning that the RMSE of Dir-2 is higher. Less error in Dir-1 is observed in P3 too. Regarding high error predictions, Dir-2 is clearly superior to Dir-1 in P1; however, Dir-1 has slightly better performance than Dir-2 in P2 and P3.

 

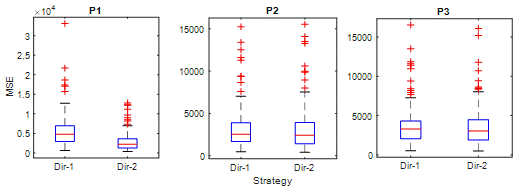
Fig. 9. MSE boxplots of Dir-1 and Dir-2 for time periods

 

MSE is a suitable criterion for evaluating a model's ability to predict unexpected values. In Figure 9 and P1, MSE values of Dir-2 are significantly lower than Di-1. In the box diagrams for P2 and P3, Dir-2 errors are slightly more than Dir-1. This situation is similar to RMSE results. On the other hand, the number of outliers in MSE is higher than other criteria. This indicates that both strategies are likely to make extremely high errors for some observations.

Analysis results show that traffic flow predictions of the LSTM and DirRec strategy have significantly higher errors. On the other hand, Dir-2 is the best strategy for P1 compared to Dir-1 and DirRec. For P2 and P3, the Dir-1 strategy may be preferred, although Dir-2 seems better on average.

 

 

4.    CONCLUSION

 

In this study, the capabilities of the LSTM model were investigated with various numerous datasets for the traffic flow prediction task. To our knowledge, this study is the first that proves the effect of using different multi-step ahead forecasting strategies on the LSTM performance. The modelling and analyses show that it is not proper to use the DirRec strategy together with LSTM in traffic flow prediction. Further, for the near future parts of the forecast horizon (P1), choosing Dir-2 makes a less average error than the Dir-1 strategy. However, for the middle and distant parts of the forecast horizon, using the Dir-1 strategy can be helpful. The results obtained here may have implications for understanding the LSTM traffic flow prediction performance tendency. Thus, more efficient approaches can be developed for certain systems, for example, TMS and ITS. There are various strategies in the literature. Despite the success shown, an important limitation is the examination of only some of these various strategies. Conducting further studies that include other strategies will advance information on the subject. Consequently, researchers should be aware of the fact that different forecasting strategies can improve LSTM performance significantly and vice versa.

 

 

References

 

1.        Ahmed M.S., A.R. Cook. 1979. "Analysis of Freeway Traffic Time-Series Data by Using Box-Jenkins Techniques". Transportation Research Record. DOI: 10.3141/2024-03.

2.        Nagel K., M. Schreckenberg. 1992. "A cellular automaton model for freeway traffic". Journal de Physique I. DOI: 10.1051/jp1:1992277.

3.        Cremer M. 1995. "On the calculation of individual travel times by macroscopic models". Pacific Rim TransTech Conference. Vehicle Navigation and Information Systems Conference Proceedings. 6th International VNIS. A Ride into the Future. IEEE; 1995. P. 187-193. DOI: 10.1109/VNIS.1995.518837.

4.        Williams B.M. 2001. "Multivariate vehicular traffic flow prediction: Evaluation of ARIMAX modeling". Transportation Research Record. DOI: 10.3141/1776-25.

5.        Wu C.H., J.M. Ho, D.T. Lee. 2004. "Travel-Time Prediction With Support Vector Regression". IEEE Transactions on Intelligent Transportation Systems 5(4): 276-281. DOI: 10.1109/TITS.2004.837813.

6.        Audu Akeem A., Olufemi F. Iyiola, Ayobami A. Popoola, Bamiji M. Adeleye, Samuel Medayese, Choene Mosima, Nunyi Blamah. 2021. "The application of geographic information system as an intelligent system towards emergency responses in road traffic accident in Ibadan". Journal of Transport and Supply Chain Management 15(a546): 1-17. ISSN 2310-8789.

7.        Paľo Jozef, Ondrej Stopka. 2021. "On-Site Traffic Management Evaluation and Proposals to Improve Safety of Access to Workplaces". Communications 23(3): A125-A136. University of Zilina.

8.        Hossan Sakhawat, Naushin Nower. 2020. "Fog-based dynamic traffic light control system for improving public transport". Public Transport 12: 431-454.

9.        Danilevičius Algimantas, Marijonas Bogdevičius, Modesta Gusarovienė, Gediminas Vaičiūnas, Robertas Pečeliūnas, Irena Danilevičienė. 2018. “Determination of Optimal Traffic Light Period Using a Discrete Traffic Flow Model”. Mechanika 24(6): 845-851.

10.    Pranevičius Henrikas, Tadas Kraujalis. 2012. "Knowledge based traffic signal control model for signalized intersection". Transport 27(3): 263-267.

11.    Zhong M., S. Sharma, P. Lingras. 2005. "Short-Term Traffic Prediction on Different Types of Roads with Genetically Designed Regression and Time Delay Neural Network Models". Journal of Computing in Civil Engineering 19(1): 94-103. DOI: 10.1061/(ASCE)0887-3801(2005)19:1(94).

12.    Smith B.L., B.M. Williams, R. Keith Oswald, R.K. Oswald. 2002. "Comparison of parametric and nonparametric models for traffic flow forecasting". Transportation Research Part C: Emerging Technologies 10(4): 303-321. DOI: 10.1016/S0968-090X(02)00009-8.

13.    Kamarianakis Y., P. Prastacos. 2003. "Forecasting Traffic Flow Conditions in an Urban Network: Comparison of Multivariate and Univariate Approaches". Transportation Research Record 1857(1): 74-84. DOI: 10.3141/1857-09.

14.    Kumar B. Anil, Vivek Kumar, Lelitha Vanajakshi, Shankar C. Subramanian. 2017. "Performance Comparison of Data Driven and Less Data Demanding Techniques for Bus Travel Time Prediction". European Transport \ Trasporti Europei 65(9): 1-17. ISSN 1825-3997.

15.    Hochreiter S., J. Schmidhuber. 1997. "Long Short-Term Memory". Neural Computation 9(8): 1735-1780. MIT Press Journals. DOI: 10.1162/neco.1997.9.8.1735.

16.    Fu R., Z. Zhang, L. Li. 2016. "Using LSTM and GRU neural network methods for traffic flow prediction". 31st Youth Academic Annual Conference of Chinese Association of Automation (YAC). IEEE. P. 324-328.

17.    Luo X., D. Li, Y. Yang, S. Zhang. 2019. "Spatiotemporal traffic flow prediction with KNN and LSTM". Journal of Advanced Transportation. Hindawi.


 

18.    Yang B., S. Sun, J. Li, X. Lin, Y. Tian. 2019. "Traffic flow prediction using LSTM with feature enhancement". Neurocomputing 332: 320-327. Elsevier B.V. DOI: 10.1016/j.neucom.2018.12.016.

19.    Mou L., P. Zhao, H. Xie, Y. Chen. 2019. "T-LSTM: A Long Short-Term Memory Neural Network Enhanced by Temporal Information for Traffic Flow Prediction". IEEE Access 7: 98053-98060. DOI: 10.1109/ACCESS.2019.2929692.

20.    Li Z., G. Xiong, Y. Chen, Y. Lv, B. Hu, F. Zhu, et al. 2019. "A Hybrid Deep Learning Approach with GCN and LSTM for Traffic Flow Prediction". IEEE Intelligent Transportation Systems Conference (ITSC). P. 1929-1933. DOI: 10.1109/ITSC.2019.8916778.

21.    Ben Taieb S., G. Bontempi, A.F. Atiya, A. Sorjamaa. 2012. "A review and comparison of strategies for multi-step ahead time series forecasting based on the NN5 forecasting competition". Expert Systems with Applications 39(8): 7067-7083. Elsevier Ltd. DOI: 10.1016/j.eswa.2012.01.039.

22.    Du P., J. Wang, W. Yang, T. Niu. 2018. "Multi-step ahead forecasting in electrical power system using a hybrid forecasting system". Renewable Energy 122: 533-550. DOI: https://doi.org/10.1016/j.renene.2018.01.113.

23.    Papacharalampous G., H. Tyralis, D. Koutsoyiannis. 2019. "Comparison of stochastic and machine learning methods for multi-step ahead forecasting of hydrological processes". Stochastic environmental research and risk assessment 33(2): 481-514. Springer.

24.    Wang J., J. Heng, L. Xiao, C. Wang. 2017. "Research and application of a combined model based on multi-objective optimization for multi-step ahead wind speed forecasting". Energy 125: 591-613. DOI: https://doi.org/10.1016/j.energy.2017.02.150.

25.    Guermoui M., F. Melgani, C. Danilo. 2018. "Multi-step ahead forecasting of daily global and direct solar radiation: a review and case study of Ghardaia region". Journal of Cleaner Production 201: 716-734. Elsevier.

26.    Wang D., H. Luo, O. Grunder, Y. Lin, H. Guo. 2017. "Multi-step ahead electricity price forecasting using a hybrid model based on two-layer decomposition technique and BP neural network optimized by firefly algorithm". Applied Energy 190: 390-407. Elsevier.

27.    Xue P., Y. Jiang, Z. Zhou, X. Chen, X. Fang, J. Liu. 2019. "Multi-step ahead forecasting of heat load in district heating systems using machine learning algorithms". Energy 188: 116085. DOI: https://doi.org/10.1016/j.energy.2019.116085.

28.    Ojeda L.L., A.Y. Kibangou, C.C. Wit. 2013. "Adaptive Kalman filtering for multi-step ahead traffic flow prediction". American Control Conference. P. 4724-4729.

29.    Zhang Y., Y. Zhang, A. Haghani. 2014. "A hybrid short-term traffic flow forecasting method based on spectral analysis and statistical volatility model". Transportation Research Part C: Emerging Technologies 43: 65-78. DOI: 10.1016/j.trc.2013.11.011.

30.    Zhan X., S. Zhang, W.Y. Szeto, X.M. Chen. 2018. „Multi-step-ahead traffic flow forecasting using multi-output gradient boosting regression tree”. Transportation Research Board 97th Annual Meeting. Washington DC, United States. 2018-1-7 to 2018-1-11.

31.    Jain A.K. 2010. "Data clustering: 50 years beyond K-means". Pattern Recognition Letters 31(8): 651-666. DOI: 10.1016/j.patrec.2009.09.011.

32.    Arthur D., S. Vassilvitskii. 2007. „k-means++: The advantages of careful seeding”. SODA '07: Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms. P. 1027-1035. Stanford.

 

33.    Arima C., K. Hakamada, M. Okamoto, T. Hanai. 2008. "Modified fuzzy gap statistic for estimating preferable number of clusters in fuzzy k-means clustering". Journal of bioscience and bioengineering 105(3): 273-281. Elsevier.

34.    Song X., Y. Liu, L. Xue, J. Wang, J. Zhang, J. Wang, et al. 2020. "Time-series well performance prediction based on Long Short-Term Memory (LSTM) neural network model". Journal of Petroleum Science and Engineering 186: 106682. Elsevier.

35.    Ben Taieb S., G. Bontempi, A.F. Atiya, A. Sorjamaa, S. Ben Taieb, G. Bontempi, et al. 2012. "A review and comparison of strategies for multi-step ahead time series forecasting based on the NN5 forecasting competition". Expert systems with applications 39(8): 7067-7083. Elsevier. DOI: 10.1016/j.eswa.2012.01.039.

36.    Chang L.C., M.Z.M. Amin, S.N. Yang, F.J. Chang. 2018. "Building ANN-based regional multi-step-ahead flood inundation forecast models". Water 10(9): 1283. Multidisciplinary Digital Publishing Institute.

37.    Zhan X., S. Zhang, W.Y. Szeto, X. Chen. 2019. "Multi-step-ahead traffic speed forecasting using multi-output gradient boosting regression tree". Journal of Intelligent Transportation Systems. P: 1-17. Taylor & Francis.

38.    Tran V.T., B.S. Yang, A.C.C. Tan. 2009. "Multi-step ahead direct prediction for the machine condition prognosis using regression trees and neuro-fuzzy systems". Expert Systems with Applications 36(5): 9378-9387. DOI: https://doi.org/10.1016/j.eswa.2009.01.007.

39.    Sorjamaa A., A. Lendasse. 2006. "Time series prediction using DirRec strategy". Esann. P. 143-148.

40.    Sorjamaa A., J. Hao, N. Reyhani, Y. Ji, A. Lendasse. 2007. "Methodology for long-term prediction of time series". Neurocomputing 70(16-18): 2861-2869. Elsevier.

41.    PeMS. PeMS Data Clearinghouse. Available at: http://pems.dot.ca.gov/?dnode=Clearinghouse.

42.    Mydhili S.K., S. Periyanayagi, S. Baskar, P.M. Shakeel, P.R. Hariharan. 2019. "Machine learning based multi scale parallel K-means++ clustering for cloud assisted internet of things". Peer-to-Peer Networking and Applications. P. 1-13. Springer.

43.    Qiu X., Y. Zhang. 2019. "A Traffic Speed Imputation Method Based on Self-adaption and Clustering". IEEE 4th International Conference on Big Data Analytics (ICBDA). P. 26-31. IEEE.

44.    Sharma D., K. Thulasiraman, D. Wu, J.N. Jiang. 2019. "A network science-based
k-means++ clustering method for power systems network equivalence". Computational Social Networks 6(1): 4. Springer.

45.    Lalle Y., M. Abdelhafidh, L.C. Fourati, J. Rezgui. 2019. "A hybrid optimization algorithm based on K-means++ and Multi-objective Chaotic Ant Swarm Optimization for WSN in pipeline monitoring". 15th International Wireless Communications & Mobile Computing Conference (IWCMC). P. 1929-1934. IEEE.

46.    Davies L., U. Gather. 1993. "The identification of multiple outliers". Journal of the American Statistical Association 88(423): 782-792. DOI: 10.1080/01621459.1993.10476339.

47.    Caliński T., J. Harabasz. 1974. "A dendrite method for cluster analysis". Communications in Statistics-theory and Methods 3(1): 1-27. Taylor & Francis.

48.    Tibshirani R., G. Walther, T. Hastie. 2001. "Estimating the number of clusters in a data set via the gap statistic". Journal of the Royal Statistical Society: Series B (Statistical Methodology) 63(2): 411-423. Blackwell Publishers Ltd. DOI: 10.1111/1467-9868.00293.

49.    Rousseeuw P.J. 1987. "Silhouettes: a graphical aid to the interpretation and validation of cluster analysis". Journal of computational and applied mathematics 20: 53-65.
North-Holland.

50.    MathWorks®. Gap Value. Available at: https://www.mathworks.com/help/stats/clustering.evaluation.gapevaluation-class.html.

51.    Kingma D.P., J. Ba. 2014. Adam: A method for stochastic optimization. Computer Science, Mathematics. arXiv preprint arXiv:1412.6980.

 

 

Received 15.04.2021; accepted in revised form 29.05.2021

 

 

by

Scientific Journal of Silesian University of Technology. Series Transport is licensed under a Creative Commons Attribution 4.0 International License


[1] Department of Civil Engineering, Engineering Faculty, Kırıkkale University, Yahşihan,71451, Kırıkkale, Turkey. Email: edogan@kku.edu.tr. ORCID: https://orcid.org/0000-0001-7802-641X