Article
citation information:
Sága, M., Vaško, M.,
Handrik, M., Kopas, P. Contribution to random vibration numerical simulation and optimisation
of nonlinear mechanical systems. Scientific
Journal of Silesian University of Technology. Series Transport. 2019, 103, 143-154. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2019.103.11.
Milan
SÁGA[1], Milan VAŠKO[2], Marian HANDRIK[3], Peter
KOPAS[4]
CONTRIBUTION
TO RANDOM VIBRATION NUMERICAL SIMULATION AND OPTIMISATION OF NONLINEAR
MECHANICAL SYSTEMS
Summary. This study considered the solution of the stochastic
vibration of non-linear mechanical systems with Gaussian random excitations. It
realised a short review of linearisations techniques in stochastic dynamics
mainly with application in the area of truss finite element modelling. The
presented method of statistical linearisation is applied to numerical testing.
In the second part of the article, the sensitivity analysis of the first
two stress statistical moments and structural weight minimising subjected to
the random stress constrains presented by mean value and standard deviation was
brought to the fore. Cross-sectional areas were used as optimising parameters.
Keywords: statistical
linearisation, sensitivity analysis, structural optimising
1. INTRODUCTION
Modelling and analysis of dynamic
properties of mechanical systems using linear computational tools are often the
first approximation of the actual conduct of the investigated object. The
obtained results must be considered with caution, and we must decide whether
they are sufficient for us, or we will require more detail and complex study of
the issue with the consequent formation of a more appropriate mechanical and
mathematical model. If at least one member in the model is nonlinear, then the whole
system acts as nonlinear. According to the effect of non-linear members on the
dynamic properties, we distinguished systems with significant (strong) and a
little significant (weak) nonlinearities. Of course, much more complex are
tasks with significant nonlinearities, where the ambiguity of solution
causes considerable problems.
The task difficulty may increase if
the inputs to a nonlinear system are characterised as a random process or its
parameters are random as well, and especially if the investigated processes are
non-stationary and non-Gaussian [1,25]. Several different methodical approaches
have been developed to solve such problems, applicable only to certain types of
tasks. The conditions determining the applicability of individual methods are associated
with the type of nonlinearity, its location, as well as the characteristics of
random processes operating in the system [1,25].
The most common but simplest
nonlinearity is the static
transformation (non-inertial), characterised by the following equation
. (1)
Equation
(1) presents the functional dependency between the restoring force in a spring
and the spring strain. A mechanical system with nonlinearity solved in a static
sense is usually a rare phenomenon. In technical practice, we encounter special
systems that do not allow neglecting the inertial and dissipative effects. This
means that equation (1) in general is no longer a nonlinear algebraic equation,
but a nonlinear differential equation. Kropáč in [14] divides
the methods of solving such tasks into the methods of a local nature that well describes the behaviour of a system in a
relatively small surrounding of a certain (working) point usually in
equilibrium. There are known linearisation approaches that have experienced
considerable success in various applications in the engineering practice. In
contrast, there are methods of global
nature that describe the behaviour of a system in a broader sense,
that is, in the entire scope of variables. Solution of a specific task depends
on the solvers and their ability to identify the nature of the problem and
predict the solution.
As already mentioned, there are a
number of independent approaches built on different principles that give
acceptable results based on certain assumptions. The global approaches include
analysis of nonlinear dynamic systems using the theory of Markov processes,
which leads to solving the familiar equation by Fokker-Planck-Kolmogorov (FPK) [2,5]. In practice, we often
encounter local approaches represented by the method of statistical
linearisation in various modifications (Krylov, Bogoliubov, Caughey, Bolotin
[2], Kazakov [12], Nigam [16], Roberts, Spanos [18,23], Elishakoff [7]), method
of statistical quadratisation (Spanos, Donley [22]), functional method by
Volterra and Wiener [14,24]. In addition to the above-mentioned methods, which
have been the most discussed ones in the recent decade, other methods have been
developed in the past, such as the asymptotic method by
Krylov-Bogoliubov-Mitropolsky [2,12], suitably adapted methods of the small
parameter, especially the perturbation version [16], harmonic linearisation [2]
and mean values [2]. Thanks to computer technology also other methods have been
given a green light, based on simple but time-consuming and computationally
intensive approaches. In particular, there are simulation methods in various
modifications. Simulation approaches solve dynamic tasks directly in the time
domain, which is demanding on computation time. If we add to the above the random
nature of excitation and the need to obtain a complete picture of system
behaviour for various excitation realisations, then we come to the Monte Carlo
method [1,10,19,20]. Other authors have explored ways of increasing efficiency
by combining the Monte Carlo method with the other aforementioned methods (for
example, a combination of statistical linearisation and the Monte Carlo
method [7]).
2. METHOD OF EQUIVALENT
STATISTICAL LINEARISATION
Equivalent statistical
linearisation (ESL) has been used for a relatively long period to deal with
randomly excited nonlinear systems, especially in the frequency domain. It is
an approximation method, in which solving a system of nonlinear differential
equations is replaced by solving an equivalent linear system suitable to obtain
the Fourier transform of the system. The method was first presented by Krylov
and Bogoliubov [2,12], and further elaborated by Booton [1,2], Caughey [21],
Kazakov [12], Iwan, Yang [22], Spanos [23], then evaluated by Roberts and
Spanos in [18]. The development of ESL within nonlinear stochastic dynamics is
also associated with the works of Foeter [23], Malhotra and Penzien [24],
Iwan and Yang [21], Atalik and Utku [18], Iwan and Mason [24],
Brücker and Lin [21], as well as many others. Especially, the 1960s
to 1980s were a period of enormous increase in method applications.
We obtain the parameters
of an equivalent linear system by satisfying a certain pre-selected criterion,
under which we assess the conformity of the original and linearised model
especially in the outputs that are characterised mainly by statistical moments.
By their very nature, the presented techniques are a generalisation of
deterministic linearisation methods by Krylov and Bogoliubov. The most
frequently used criteria include:
· criterion based on
energy balance of an actual and equivalent model,
· criterion of conformity
of the corresponding mean values and response dispersions of the original
and linearised nonlinear function with a random input (less suitable),
· criterion of the minimum
root-mean-square deviation of an actual and approximated (linearised, or
squared) function.
It should be noted that,
on one hand, the advantages of this method certainly include its simplicity and
admissible estimate of the first two statistical moments, but on the other
hand, the change in nature of the random variable in the output, for example,
the Gaussian output does not correspond to the Gaussian input, as contemplated
by the method’s theoretical foundations. A significant shortcoming of ESL
is the possible incompatibility in the spectral response of an actual and
linearised system (for example, the difference in the characteristics of the
function of power spectral density, etc.).
For a system with
multiple degrees of freedom, we present a generalised solution methodology
based on the procedure applied by Spanos and Donley in [20] to the method of
equivalent statistical quadratisation. Let’s consider a system of
nonlinear differential equations in the form
, (2)
where M, B, K are the matrices of mass, damping and stiffness of the
linear part of the system, x(t) is the vector of unknown
displacements, f(t) is the vector
of random excitation and 
is the vector of
nonlinear forces that are a function of velocity and displacement. Let’s
assume the solution
, (3)
where mx is the vector of displacement mean values, xc is the vector of stationary
centered displacements that, however, in general do not necessarily have
Gaussian character. If we substitute (3) into (2), we obtain
. (4)
We calculate the vector of the
system response mean values as follows
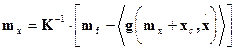, (5)
where 
is the mean value
of the vector of nonlinear forces, and mf
is the vector of the mean values of the load forces vector f(t). The load forces vector
f(t) can be expressed in the
form
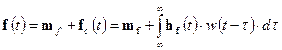, (6)
where fc(t) is the centred load
component, of which we assume to have a Gaussian character, w(t)
is the above-mentioned centred random function with a “white
noise” character. Then, the excitation power spectral density matrix
is
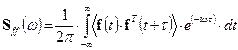or 
, (7,8)
where (*) is the symbol for a
complex conjugate (matrix), Sww is the
power spectral density of the function w(t) = 2p×d(t) and is equal to 1, Hf (w) is the Fourier transform of the impulse function hf (t). The response centred component can be determined from the
equation
. (9)
We replace this
"original" nonlinear system with an "equivalent linear"
system
, (10)
where ai are the equivalent linearisation matrices that we
determine from the condition of minimum root-mean-square deviation of
differences between the functional values of the actual and linearised
function, that is
. (11)
Parameter e is thus the vector of residuals
defined as follows
. (12)
By substitution of (12) to the condition (11) we obtain the system
, (13)
where the
vector 
has dimensions 2n´1, the symbol < > represents again the mean value operator, A is the matrix of linearisation coefficients a1 and a2 with dimension 2n´n in the form
(14)
and the
matrix of right-hand sides GN has dimension 2n´n and the form
. (15)
The system (13)
represents n linear systems with 2n unknowns. The resulting equivalent
system for centred component will be in the form (10).
In technical practice, we often encounter tasks where input to the
system is the power spectral density (PSD) matrix of excitation. Then, we
calculate the response according to known equations for linear systems, that is
, (16)
where the
frequency response of a linearised system is
, (17)
the PSD
input matrix is
(18)
and Sxx(w) will naturally be the PSD output (response) matrix, which
determines the spectral properties of the system and by its integration we
determine an estimate of second-order statistical moments (variance). The mean
value is determined from (5). The actual implementation of the calculation can
only be carried out iteratively, since the matrices a1 and a2
contain information about the first two statistical moments. The task leads to
solving a system of 2n nonlinear
equations, that is to (5) and
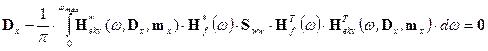, (19)
where Dx is the matrix of variances (we are
mainly interested in diagonal elements). It is usually challenging to perform
the initial estimate of mx and Dx,
therefore it is preferable to first carry out the calculation only with the
linear part of the system, and then calculate the matrices a1 and a2 from the results
obtained. These matrices then get more specific in each iterative step. The
calculation is completed when the pre-defined convergence criterion is
satisfied.
3. STATISTICAL
LINEARISATION OF GEOMETRICALLY NONLINEAR ROD FINITE ELEMENTS
Our aim is to present
possible ways of analysing geometrically nonlinear rod systems excited by
random forces. First, for simplicity, we expressed the total Lagrange’s
formulation of geometrical nonlinearity of a plane rod (truss) according to [3,26].
We know that for relative elongation the following relation applies
, (20)
where ue = [u1, u2, u3, u4]
is the unknown nodal displacement vector, the matrices BL and BNL have the form
, (21)
where a is the rod (truss) length. Internal forces in the element are
expressed as follows
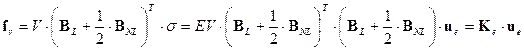. (22)
Let V be the rod volume (V = const.),
s is the normal stress in
the element, Ke is the nonlinear rod stiffness matrix, fv = [fv1, fv2, fv3, fv4]T is the vector of internal
forces, for which applies that fv3 = -fv1 and fv4 = -fv2. Then, the
forces fv1 and fv2 will be
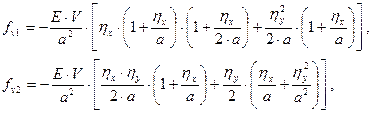(23)
where hx = u3 - u1 and hx = u4 - u2. Nonlinear relations (23)
must be “linearised” in accordance with the statistical
linearisation method, that is, create a linear equivalent model. We are
building on the theoretical basis described in the previous subchapter.
Let us resolve the vectors of displacement and internal forces into a
unidirectional component and a centred random component, that is
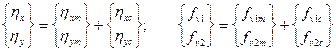. (24)
If we apply the criterion
(11), we obtain a system of equations (13) that in our case is as follows
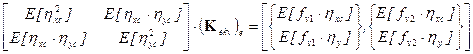. (25)
We solve the system (25)
numerically, which generalises the procedure also for application to other
types of finite elements with the only difference that the dimension of
matrices will change. In simpler cases, such as ours, (Kekv)e
can be determined analytically, as presented in [3] by Cherng and Wen. They
expressed the internal forces using the following equivalent relations
(26)
with the ultimate notation of the
equivalent relation between the internal forces vector fv and the displacement vector
ue
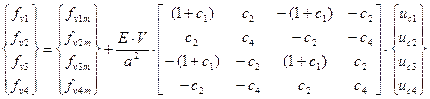(27)
or
. (28)
The matrices Klin and KSL represent the linear and
linearised component of the resulting stiffness matrix of plane rod element. We
calculate the mean values fv1m and fv2m
using the following equations (29) and (30)
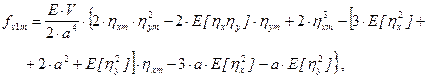(29)
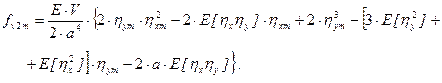(30)
The linearisation coefficients will be as follows:
c1 = [6a.hxm + 3E(hx2) + 3E(hy2)] / 2a2, c2 = [a.hym + E(hxhy)] / a2,
c3 = [a.hym + E(hxhy)] / a2, c4 = [2a.hxm + E(hx2) + 3E(hy2)] / 2a2.
After applying globalisation "FEM" procedures to compile
linearised equations of motion we obtain
. (31)
By dividing the equation
(6.82) into unidirectional and centred alternating parts we obtain a system of
equations
and 
. (32, 33)
From the theory of
stochastic processes for systems with Gaussian distribution [4,8], and
provided that the input power spectral
density (PSD) Sff (w) is known, we can rewrite the equation of state (33) into the form
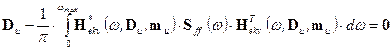, (34)
where the equivalent transfer is
calculated as follows
(35)
and B is the Rayleigh damping
matrix (B = a.M + b.K). The above procedure was based on
the total Lagrange formulation of geometric nonlinearity defined for a rod
(truss) element. However, it is generally known that the effect of nonlinearity
under consideration is much greater in the case of hyper-elastic materials than
in the case of metal materials, where the nonlinear component has a character
of "weak nonlinearity".
4. SENSITIVITY ANALYSIS AND OPTIMISATION
Optimal design in terms of
selected properties is an important part of solving problems in machine
mechanics. Most often, it is a standard strength design, which is not always
sufficient, even in some cases insufficient. The optimal design may also
include spectral tuning [8,11,15], or a design from the perspective of other
dynamic system properties [7,14]. A vast development of optimum design of
mainly linear problems in continuum mechanics was noted in the 1980s [17].
Optimisation is on the decline in recent years and the main focus is on the
optimal design of nonlinear systems.
Therefore, let us consider
thinking about optimising the geometrically nonlinear rod (truss) structures
with random inputs, sensitivity analysis [9], and the suitability of some
optimisation approaches. The part of many software systems created mainly on the basis of FEM is
sensitivity analysis. It is part of the gradient optimisation strategy of all types. Gradient
information always tells us more about the impact or significance of each
optimisation variable on the monitored mechanical quantities (displacements,
stresses, accelerations, etc.). The sensitivity analysis process can be
considered as a selection process for the subsequent calculation of significant
optimisation variables [11,17]. It is the calculation of gradients by exact way
or by apn proximation procedure. In the first case, the gradient or the
gradient matrix (sensitivity matrix) is expressed exactly. In the second case,
the relevant derivations are calculated using known numerical equations.
Nonlinearity brings
considerable complexity to this process, especially in the case of analytical
expression of the necessary derivation. Let us show how the problems in the
case of stress sensitivity analysis of the truss element are mentioned.
We are searching a derivation
of the average stress in the j-th element according to the i-th cross-sectional area (optimisation
variable Xi)
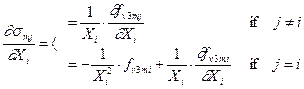(36)
where the derivation of fv3mj = - fv1mj according to Xi is generally obtained by derivation
of (29). The calculation of the stress dispersion derivation in the j-th element of i-th cross-sectional area will be
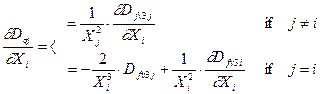(37)
where the derivative of the variance Dfv3j according to Xi is generally obtained by deriving the
matrix of dispersions of the internal forces of the j-th element
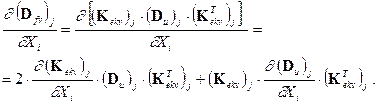(38)
Since (Kekv)j is a function of the displacement dispersion matrix (Du)j
and the average values of the displacement
vector (um)j, it is a very complex task. The centre of the presented analysis will be the calculation of the global
vector derivation of the displacements average values um and the global matrix of displacements variance Du according
to Xi. We obtain a system of nonlinear
algebraic equations by derivation of state equations (5 and 34)
,
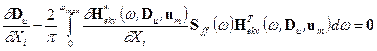. (39)
The system of equations (39)
can only be solved iteratively, which of course reduces the effectiveness of
this approach. The advantage of exact procedures in sensitivity analysis, based
on a smaller number of numerical analyses loses the timeliness, hence,
numerical derivation is more appropriate.
5. NUMERICAL EXAMPLE
We will design the
cross-sectional areas of the rod structure considering three optimisation groups of the same
cross-section. The first group of elements consists of rods 8 to 14 with
cross-sectional area A1,
second rods 15 to 25 with area A2
and third rods 1 to 7 with area A3. The loading force F has a random character of
frequency-limited "Gaussian white noise" with PSD: Sff = 15·106 [N2.s]
and with average value Fm = 1·105 [N].
The solution will be implemented in the frequency range á0,300ñ [Hz]. Other calculation parameters: material damping coefficient bc = 10-6, Young modulus E = 2,1·1011 [Pa]
and dimensions of the construction are a = 0.8 [m],
b = 0.8 [m].
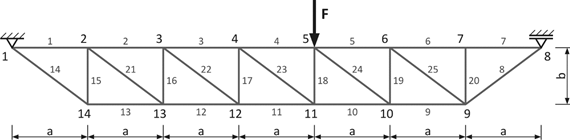
Fig. 1. Analysed rod
(truss) structure
Solving task was formulated as
an optimisation problem with stress restrictions. Three optimisation variables A1, A2, A3
and the objective function (mass of the structure) were considered in the form
,
where n is the number of rods, r is the density of the material, li is the length of the i-th rod, Ai is the
cross-sectional area of the i-th rod
with a value of A1, A2 or A3,
depending on
which optimisation group it belongs to.
The restrictive conditions
were bound to the first two statistical moments of stresses in the elements
with the following values smdov = 50 [MPa] for the average values of
stresses in the elements and sDdov = 60 [MPa] for the standard deviations. The mathematical notation of the
restrictive conditions is as follows:
- for average values: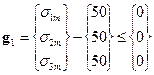 
, where 
,
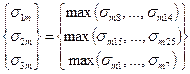where sm1, sm2, ..., sm25 are absolute values of the average stresses in the individual elements.
- for standard deviations: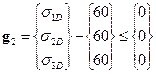 
, where 
,
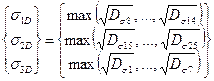where 
are standard deviations of
stresses in the individual elements.
The Nelder-Mead optimisation
algorithm built in MATLAB was used to solve our optimising problem. Selected
results of the optimisation process are processed in Tables 1 to 4 and
graphically in Figure 2.
Tab. 1
Objective function
|
Construction weight |
Start value |
Result value |
|
W [kg] |
1052.3 |
453.6 |
Tab. 2
Design
variables for individual optimisation groups
|
optimisation variable |
Start value |
Result value |
|
A1 [m2] |
6.0·10-3 |
3.51·10-3 |
|
A2 [m2] |
6.0·10-3 |
1.63·10-3 |
|
A3 [m2] |
6.0·10-3 |
3.43·10-3 |
Tab. 3
Maximum of average stress values for each optimisation group
|
Average stress |
Start value |
Result value |
|
s1m [MPa] |
30.21 |
49.89 |
|
s2m [MPa] |
14.25 |
50.13 |
|
s3m [MPa] |
30.22 |
50.21 |
Tab. 4
Maximum of standard deviations of stresses
calculated for individual optimisation groups
|
Standard deviation
of stress |
Start value |
Result value |
|
s1D [MPa] |
39.79 |
57.62 |
|
s2D [MPa] |
24.53 |
54.17 |
|
s3D [MPa] |
38.47 |
55.83 |
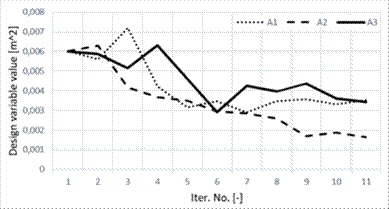
Fig. 2. Analysed
rod (truss) structure
Minor changes in stress
distribution not only for average values but also for standard deviations can
be determined from processed results. This was caused by the applied geometric
nonlinearity as well as the optimisation process itself as documented in Tables
3 and 4. Consideration of nonlinear analysis computationally complicated the
task, but results do not differ significantly from linear stochastic analysis.
The reason may be that the geometric nonlinearity of oscillating rod structures
does not appear significantly as in other cases.
6. CONCLUSION
Methods of nonlinear analysis
and optimisation of mechanical systems are certainly a topical issue today.
Many approaches based on simplifying assumptions of different importance have
been suggested in the past. Some approaches, especially from the numerical
point of view, have succeeded, some have lost importance. This also happened in
stochastic nonlinear dynamics. Due to the strong hardware support, time-based
Monte Carlo simulations [10] are now preferred, but the application of
linearisation techniques remains a useful tool for frequency domain solutions.
The approaches of statistical linearisation are an interesting alternative in
connection with finite elements with geometric or material nonlinearity.
Structural optimisation is an
essential part of creating and analysing virtual models of structures in
construction, engineering or other industries. The results of the presented
study confirm that the optimum design of nonlinear model parameters is specific
compared to linear models. Nonlinearities can cause significant changes not
only in the optimisation process itself [6], but also in the end results, overestimating
or underestimating the first two statistical moments. In conclusion, the
optimal design of a nonlinear mechanical system leads to the striking
result that cannot be predicted in advance. Therefore, a basic linear analysis
of simplified physical models alone cannot be relied upon in design. It is
necessary to get as close as possible to reality and it is often non-linear.
Acknowledgement
This work was supported by the grant agency KEGA
project No. 015ŽU-4/2017 and grant agency VEGA project No. 1/0073/19.
References
1.
Bendat
Julius S. 1990. Nonlinear system analysis
and identification from random data. New York: John Wiley & Sons.
2.
Brepta
Rudolf, Ladislav Půst, František
Turek. 1994. Mechanical vibration. Technical handbook. Praha: Sobotáles.
3.
Cherng
Rwey-Hua., Wen Yi-Kwei. 1991. „Stochastic
finite element analysis of non-linear plane trusses”. Int. Journal Non-Linear Mechanics 26(6):
835-849.
4.
Dekýš
Vladimír, Alžbeta Sapietová, Ondrej Števka.
2014. „Understanding of the dynamical properties of machines
based on the interpretation of spectral measurements and FRF”. Experimental stress analysis 51. Applied Mech. and Materials 486:
106-112.
5.
Dobiáš
Ivan. 1988. Nonlinear dynamic systems
with random inputs. Praha: Academia.
6.
Dodok
Tomáš, Nadežda Čuboňová, Miroslav
Císar, Ivan Kuric, Ivan Zajačko. 2017. „Utilization
of strategies to generate and optimize machining sequences in CAD/CAM”. Procedia Engineering 192: 113-118. ISSN
1877-7058.
7.
Elishakoff
Isaac, Pierluigi Colombi. 1993. „Successful combination of the stochastic
linearization and Monte Carlo methods”. J. of Sound and Vibration 160(3): 554-558.
8.
Frankovský
Peter, Darina Hroncová, Ingrid Delyová, Peter Hudák. 2012.
„Inverse and forward dynamic analysis of two link
manipulator”. Procedia Engineering
48: 158-163.
9.
Flizikowski Jozef, Marek Macko, Jacek Czerniak., Adam Mroziński.
2011. „Implementation of genetic algorithms into development
of mechatronic multi-edge's grinder design”, In ASME 2011 International Mechanical Engineering Congress and Exposition,
IMECE. Nov. 11-17, 2011, Denver, Colorado, USA.
10.
Gerlici
Juraj, Tomáš Lack. 2014. „Modified HHT Method for vehicle vibration
analysis in time domain utilisation”. Applied
Mechanics and Materials 486: 396-405.
11.
Homišin
Jaroslav, Robert
Grega, Peter Kaššay, Gabriel Fedorko, Vieroslav Molnár. 2019. “Removal
of systematic failure of belt conveyor drive by reducing vibrations”. Engineering Failure Analysis 99: 192-202. ISSN
1350-6307.
12.
Kazakov Igor J. 1983. Analysis
of the stochastic system in the space of states. Moskow: Nauka.
13.
Krawiec Piotr, Grzegorz Domek, Łukasz Warguła, Konrad
Waluś, Jarosław Adamiec. 2018.
„The application of the optical system ATOS II for
rapid prototyping methods of non-classical models of cogbelt pulleys”. MATEC Web of Conferences 157 (01010).
14.
Kropáč
Oldřich. 1987. Random
effects in mechanical systems. Prague: SNTL.
15.
Mazurkiewicz
D. 2010. „Tests of extendability and strength of adhesive-sealed joints
in the context of developing a computer system for monitoring the condition of
belt joints during conveyor operation”. Eksploatacja i Niezawodnosc – Maintenance and Reliability 3:
34-39.
16.
Nigam
N.C. 1983. Introduction to Random
Vibrations. Cambridge : MIT Press.
17.
Olsen
Gregory R., Vanderplaats Garret N. 1989. „Method for Nonlinear Optimization with
Discrete Design Variables”. AIAA
Journal 27(11): 1584-1589.
18.
Roberts
John B., Pol D. Spanos. 1990. Random
Vibrations and Statistical Linearization. New York: John Wiley & Sons.
19.
Shinozuka
Masanobu. 1972. „Monte Carlo simulation of structural
dynamics”. Computer and Structures
2: 865-874.
20.
Smutny
J., V. Nohal, D. Vukusicova, H. Seelmann. 2018. “Vibration analysis by
the Wigner-Ville transformation method”. Komunikacie 4. ISSN: 1335-4205.
21.
Soong
T.T., M. Grigoriu. 1993. Random Vibration
of Mechanical and Structural Systems. Prentice-Hall: Englewood Cliffs.
22.
Spanos
Pol D., M.G. Donley. 1991. „Equivalent statistical quadratization for
nonlinear systems”. Journal of
Engineering Mechanics ASCE 117:
1289-1309.
23.
Spanos
Pol D. 1981. „Stochastic linearization in structural
dynamics”. Applied Mechanics
Reviews 34(1): 1-8.
24.
To Cho
W.S. 2000. Nonlinear Random Vibration:
Analytical Techniques and Applications. Lise, Netherlands: Swets &
Zeitlinger B.V.
25.
Turygin
Yuri, Pavol Božek, Ivan V. Abramov, Yury R. Nikitin.
2018. „Reliability determination and diagnostics of a
mechatronic system”. Advances in
Science and Technology Research Journal 12(2): 274-290.
26.
Wen
Y.K. 1989. „Methods of random vibration for inelastic
structures”. Applied Mechanics
Reviews 42: 39-52.
27.
Zul'ová
L., R. Grega, J. Krajňák. 2017. „Optimization of noisiness of
mechanical system by using a pneumatic tuner during a failure of piston
machine”. Engineering Failure
Analysis 79: 845-851. ISSN 1350-6307.
Received 05.01.2019; accepted in revised form 04.05.2019
Scientific
Journal of Silesian University of Technology. Series Transport is licensed
under a Creative Commons Attribution 4.0 International License