Article citation information:
Korkmaz, E., Akgungor, A.P. Estimation of passenger-kilometer and tonne-kilometer values for highway transportation in Turkey using the flower pollination algorithm. Scientific Journal of Silesian University of Technology. Series Transport. 2018, 98, 45-52. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2018.98.5.
Ersin KORKMAZ [1], Ali
Payidar AKGUNGOR[2]
ESTIMATION
OF PASSENGER-KILOMETER AND TONNE-KILOMETER VALUES FOR HIGHWAY TRANSPORTATION IN
TURKEY USING THE FLOWER POLLINATION ALGORITHM
Summary. Within the scope of this study, intercity passenger
and freight movements in Turkey are estimated by using the flower pollination
algorithm (FPA), while demand forecasts are performed on transport systems
considering possible future scenarios. Since the passenger and freight
transport system in Turkey mainly involves road transport, passenger-kilometer
and tonne-kilometer values of this system are estimated. By relying on three
independent parameters, models were developed in three different forms: linear,
force and semi-quadratic. Population (P) between 1990 and 2016, gross domestic
product per capita (GDPperC) in US dollars and the number of vehicles were used
as input parameters for the development of the models. When the passenger-kilometer
models were created, the number of cars, buses and minibuses that are
predominantly used for passenger transportation was preferred for the number of
vehicles, while the number of trucks and vans used for cargo transportation
were taken into consideration in the tonne-kilometer models. The coefficients
of the models were determined by FPA optimization, with models developed to
estimate passenger-kilometer and tonne-kilometer values. The model results were
compared with the observation values and their performance was evaluated. Two
different scenarios were created to estimate passenger-kilometer and tonne-kilometer
in 2030. Parallel to the increase in population and welfare level, it is
predicted that demand for passenger and freight transport will increase. In
particular, the higher input parameter values in Scenario 1 significantly
affect the increase in demand, leading to a demand increase of around 50%. In
addition, the FPA has demonstrated effective performance in predicting the demand
for passenger and freight transport and that it can be used in many different
areas.
Keywords: passenger-kilometer,
tonne-kilometer, flower pollination algorithm
1. INTRODUCTION
Transport, defined as the rapid, economic and
secure displacement of people and goods, is a service activity created by other
sectors of demand, with industry, commerce, agriculture and tourism among the
most important sectors that generate demand. In the main, Turkey has a highway
transport system, with approximately 90% of passenger and freight transport [1]
carried out via this transportation system. The highway transportation system
brings about many problems, especially traffic accidents. It is possible to
obtain many benefits and to avoid transportation problems with the development
of transportation systems with a specific plan for and the coordination of each
transport system. For this purpose, it is necessary to determine future
transportation demands in order to create the right plans and policies.
Many researchers have been working on
forecasting transport demand for years. Different approaches have been applied
to estimate the demand for passenger and freight transport, and more realistic
models have been put forward. Garrido and Mahmassani [2] have applied the multinomial
probit model with a spatially and temporally correlated error structure to
estimate freight transport demand. The model has been successfully applied to
the actual transport data set presented by a large truck load carrier. In
addition to the substantive information obtained from the estimation results,
the predictive tests were performed to assess the predictive ability of the
model for operational purposes [11]. Haldenbilen and Ceylan [3] used
socio-economic data and developed demand prediction models using genetic
algorithms. They attempted to estimate freight and passenger movements in
intercity roads in Turkey for the period up to 2025 by using the proposed
models. Çelikoğlu and Cığızoğlu [4] conducted an
estimation of passenger flows with a generalized regression neural network and
compared them with a stochastic model. It has been shown that the proposed
model gives better results than observational results and performs better than
the statistical model. Semeida [5] developed forecasting models for travel
demand for less populated places in north-eastern Egypt with multiple linear
regression and generalized linear modelling. Demand models can provide
acceptable statistics within regions and are conceptually suitable. In
addition, this study found that the generalized linear modelling approach is
more appropriate and accurate than the regression approach. Nuzzolo and Comi
[6] developed a model for predicting the demand for urban freight in Rome,
depending on the quantity, delivery and vehicle. The developed modelling system
is multistage and considers a separate selection approach for each decision
level. The model has been tested using traffic counts and interviews with
retailers and truck drivers in the inner area of Rome. Yang [7] developed demand
prediction models for regional freight transport by applying simple linear
regression, multiple linear regression and non-linear regression approaches.
The latter approach outperformed others. Toole et al. [8] estimated travel
demand using mobile phone call records in conjunction with open and crowded
geographical data, census records and surveys. The flexibility of the developed
system has been analysed in various cities around the world.
The aim of this study is to develop simple and
practical transportation demand forecasting models based on population, GDPperC
and the number of vehicles. In addition, it seeks to demonstrate that the FPA,
one of the artificial intelligence techniques, is applicable to the estimation
of transportation demand.
2. FLOWER POLLINATION ALGORITHM
The FPA, developed by Xie-She Yang
[9] in 2012, is inspired by the reproductive behaviour of flowering plants. The
pollination method is used in the maintenance of optimal biological viability
and reproduction. There are two important forms of pollination: biotic and
abiotic. The biotic form, which takes place with pollens transferred by
pollinators, such as flying insects, has been used in the reproduction of 90%
of flower plants. The abiotic form, in which no pollinator is required, is used
in 10% of plants. This model has been developed with certain assumptions and
rules. The FPA has four basic rules and looks for the most appropriate solution
according to these rules:
- The processes of global
pollination are carried out in biotic form, while pollinators carry pollen
in the form of cross-pollination according to Lévy flights.
- Abiotic pollination and
self-pollination constitute local pollination.
- Pollinators can improve the
reproduction probability of flower constancy, which is proportional to the
similarity of the two flowers.
- Local and global pollution can
be controlled by a switching probability p ∈ [0,1].
Given that insects can fly for a
long time, pollen can be transported over long distances. This situation
guarantees the best reproduction possible. The mathematical expression of
flower constancy is shown in Equation 1.
![]() (1)
(1)
where ![]() is solution vector at iteration t and g∗ is the current best. Here, γ is a scaling factor to control the
step size.
is solution vector at iteration t and g∗ is the current best. Here, γ is a scaling factor to control the
step size.
The Lévy distribution is used to
correspond to the strength of pollination. When insects travel long distances,
the movement of insects can be represented by the Lévy distribution. Lévys
mathematical expression is shown in Equation 2.
![]() (2)
(2)
where Γ (λ) is the standard gamma
function and s is the step size. This distribution is valid for s>0 large
steps. In theory, s0ť0 is required; but, in practice, s0 can be as small as
0.1. For local pollution, both Rule 2 and Rule 3 are shown in Equation 3.
![]() (3)
(3)
where ![]() are pollen from different flowers of the same
plant species.
are pollen from different flowers of the same
plant species.
3. PASSENGER-KILOMETER AND TONNE-KILOMETER
MODELS USING THE FLOWER POLLINATION ALGORITHM
Population (P), GDPperC and the number of vehicles (V) were used as input
variables in the development of the models. These data were obtained from the
Turkey Statistical Institute [10]. During the creation of the passenger-kilometer
models, the number of cars, buses and minibuses that are generally used for
passenger transportation were used for the number of vehicles, while the number
of trucks and vans used for cargo transportation were taken into consideration
in the tonne-kilometer models. Twenty-two of the 27-year-old input parameters
between 1990 and 2016 were randomly divided and used as training data, while the rest were used as test data. The models
developed in linear, force and semi-quadratic forms are shown in Equations 4-6.
Linear form:
![]() (4)
(4)
Power form:
![]() (5)
(5)
Semi-quadratic form:
![]() (6)
(6)
Here, x1, x2 and x3
are population, GDPperC and the number of vehicles, respectively. Wis
are the coefficients of the models.
After the models were optimized
according to the FPA, the coefficients of models were obtained, as shown in
Table 1.
Tab. 1
Coefficients of the models
|
Tonne-kilometer |
||
|
Linear |
Power |
Semi-quadratic |
|
w1=10,185 |
w1=0.097 |
w1=9,979 |
|
w2=3,429,856 |
w2=1.336 |
w2=-55,146,909 |
|
w3=-11,231 |
w3=-0.285 |
w3=-175,884 |
|
w4=-481,854,122,943 |
w4=0.453 |
w4=-282,809 |
|
|
|
w5=-5,588 |
|
|
|
w6=7,115,182 |
|
|
|
w7=-371,062,336,694 |
|
Passenger-kilometer |
||
|
Linear |
Power |
Semi-quadratic |
|
w1=5,747 |
w1=0.335 |
w1=-1,223 |
|
w2=-832,688 |
w2=1.299 |
w2=-15,297,166 |
|
w3=31,827 |
w3=-0.036 |
w3=-33,060 |
|
w4=394,859,379,208 |
w4=0.256 |
w4=-910,708 |
|
|
|
w5=1,255 |
|
|
|
w6=3,939,353 |
|
|
|
w7=363,813,728,095 |
4. FINDINGS AND EVALUATION
The performance evaluation of the proposed models was
performed according to the mean absolute percentage error (MAPE) and the
coefficient of determination (R2) methods. The mathematical
expressions of the comparison criteria are given in Equations 7 and 8.
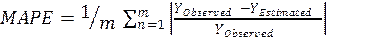 (7)
(7)
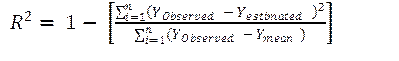 (8)
(8)
The statistical values of the passenger-kilometer and tonne-kilometer
estimation models according to training and test data are given in Table 2.
Tab. 2
Statistics for training and
test data
|
|
Passenger-kilometerm |
Tonne-kilometer |
|||||
|
|
|
Linear |
Power |
Semi-quadratic |
Linear |
Power |
Semi-quadratic |
|
Training |
MAPE |
4.1 |
6.64 |
3.09 |
6.18 |
8.15 |
5.57 |
|
R2 |
96.17 |
91.29 |
97.74 |
95.87 |
92.47 |
96.53 |
|
|
Test |
MAPE |
4.36 |
8.81 |
3.7 |
6.07 |
9.28 |
6.26 |
|
R2 |
95.98 |
92.42 |
97.74 |
97.39 |
95.06 |
97.29 |
|
When the results of the
statistics given in Table 2 are analysed as training and test data, it is
understood that the semi-quadratic model gives the best result in terms of MAPE
and R2 values and provides the closest estimate to the observation
values with minimum error. In the passenger-kilometer forecast, the performance
of the model was better than the tonne-kilometer forecast, and could be
estimated with an average error of 3%. It has been shown that, although the
performance of the linear model is worse than the semi-quadratic model, it can
be an alternative method because it is a practical and useful form. The
performance of the force model has been unsuccessful compared to other models,
while it has been observed that the estimations of this form for the passenger-kilometer
and the tonne-kilometer model are very different from the observation results
with a 9% error.
5. PASSENGER-KILOMETERM AND TONNE-KILOMETER
PROJECTION
Passenger-kilometer and tonne-kilometer values for the
future are estimated with two possible scenarios. In Scenario 1, the population
is predicted to increase by 1.7% per year on average, and it is assumed that it
will reach about 100 million in 2030. The increase in GDPperC is determined as
4% by considering the economic growth data for Turkey. The scenario is
also set by assuming that vehicle numbers will increase by 3%. In Scenario 2,
the projection of the Turkey Statistical Institute data has been used for
population growth, with the population estimated to be approximately 89 million
in 2030. The increase in GDPperC and the number of vehicles is determined by
considering the 27-year growth rate. Thus, while the number of vehicles used
for passenger transport in 2030 is approximately 19 million vehicles, it is
predicted that the number of vehicles used for freight transport will be 5.5
million. Tables 3 and 4 show the projection values of the input parameters in
Scenario I and Scenario II, respectively.
Tab. 3
Scenario I: input variable
future forecast
|
Years |
Future
projection |
|||
|
|
Population |
GDPperC |
Number of vehicles for passengers |
Number of vehicles for freight |
|
2017 |
81,171,724 |
9,739 |
12,422,372 |
4,353,173 |
|
2018 |
82,551,643 |
10,128 |
12,857,155 |
4,440,237 |
|
2019 |
83,955,021 |
10,533 |
13307,156 |
4,529,042 |
|
2020 |
85,382256 |
10,955 |
13,772,906 |
4,619,622 |
|
2021 |
86,833,755 |
11,393 |
14,254,958 |
4,712,015 |
|
2022 |
88,309,929 |
11,848 |
14,753,881 |
4,806,255 |
|
2023 |
89,811,197 |
12,322 |
15,270,267 |
4,902,380 |
|
2024 |
91,337,988 |
12,815 |
15,804,727 |
5,000,428 |
|
2025 |
92,890,734 |
13,328 |
16,357,892 |
5,100,436 |
|
2026 |
94,469,876 |
1,3861 |
16,930,418 |
5,202,445 |
|
2027 |
96,075,864 |
14,415 |
17,522,983 |
5,306,494 |
|
2028 |
97,709,154 |
14,992 |
18,136,287 |
5,412,624 |
|
2029 |
99,370,209 |
15,592 |
18,771,057 |
5,520,876 |
|
2030 |
101,059,503 |
1,6215 |
19,428,044 |
5,631,294 |
Tab. 4
Scenario II: input variable
future forecast
|
Years |
Future
projection |
|||
|
|
Population |
GDPperC |
Number of vehicles for passengers |
Number of vehicles for freight |
|
2017 |
80,550,000 |
10,670 |
12,087,653 |
4,127,815 |
|
2018 |
81,320,000 |
10,760 |
12,154,523 |
4283,771 |
|
2019 |
82,080,000 |
10,853 |
12,753,633 |
4,439,727 |
|
2020 |
82,820,000 |
10,949 |
13,369,193 |
4,595,684 |
|
2021 |
83,540,000 |
11,050 |
14,001,201 |
4,751,640 |
|
2022 |
84,250,000 |
11,154 |
14,649,657 |
4,907,596 |
|
2023 |
84,940,000 |
11,263 |
15,314,562 |
5,063,552 |
|
2024 |
85,570,000 |
11,381 |
15,995,916 |
5,219,508 |
|
2025 |
86,180,000 |
11,504 |
16,693,718 |
5,375,465 |
|
2026 |
86,780,000 |
11,631 |
17,407,968 |
5,531,421 |
|
2027 |
87,350,000 |
11,762 |
18,138,668 |
5,687,377 |
|
2028 |
87,900,000 |
11,899 |
18,885,815 |
5,843,333 |
|
2029 |
88,430,000 |
12,040 |
19,649,412 |
5,999,289 |
|
2030 |
88,930,000 |
12,188 |
20,429,456 |
6,155,245 |
According to both scenarios, the passenger-kilometer and tom-km demand for
the time period up to 2030 was forecasted using the semi-quadratic model, which
offered the best performance. The distribution graph of these estimates is
given in Figure 1.
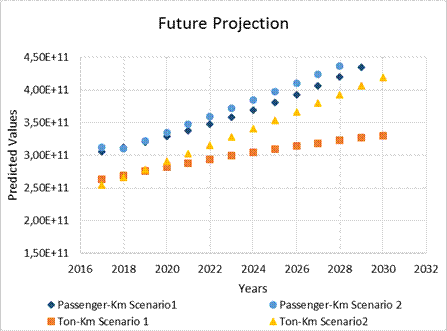
Fig. 1. Passenger-kilometer
and tonne-kilometer prediction values
In the passenger-kilometer
estimation, both scenarios showed parallel predictions, while the tonne-kilometer
estimation was expected to show a different trend according to the scenario.
6. CONCLUSION
In this study, the applicability of the FPA for the
estimation of passenger-kilometer and tonne-kilometer values in Turkey has been
demonstrated. Three different forms of road passenger and freight demand
forecasting models have been developed with statistical data covering 27 years,
and the results are presented. The best performance has been observed with the
semi-quadratic model, compared to other models. When looking at the simplicity
and suitability of the forms, it can be seen that the linear model could be
used as an effective alternative approach, even though it delivered worse
results than the semi-quadratic model.
According to different scenarios, it is expected that
the demand for passenger and freight transport will increase in parallel with
an increase in the population and the level of prosperity. In particular,
according to the input parameter values in Scenario 2, the increase in freight
and passenger demand is more than in the case of Scenario 1, while it is
predicted that demand will increase by 50%. In addition, the rate of increase
for trucks and pickups in Scenarios 1 and 2 is also reflected in the demand
increase, and it is understood from the graph in Figure 1 that there is a
linear relationship between them.
The FPA has demonstrated effective performance in predicting
passenger and freight transport demand and that it can be used in many
different areas. The effectiveness of the FPA approach will be highlighted
in future studies by comparing it to other artificial intelligence techniques.
References
1.
Aydemir H., M.K.
Çubuk. 2017. Karayollarının Türkiyede Genel Durumunun
Araştırılması ile Yaşanan Değişimler ve Gelecek
Stratejilerine Dair Tavsiyeler. [In Turkish: Changes experienced on
highways: an investigation into the general situation in Turkey and recommendations
relating to future strategies.] Gazi
Mühendislik Bilimleri Dergisi 2(3): 128-146.
2.
Garrido R.A., H.S.
Mahmassani. 2000. Forecasting freight transportation demand with space-time
multinomial probit model. Transportation
Research Part B 34: 403-418.
3.
Haldenbilen S., H.
Ceylan. 2005. Şehirler Arası Ulaşım Talebinin Genetik Algoritma ile
Modellenmesi. [From Turkish: Modelling of intercity transportation demand
with a genetic algorithm.] IMO Teknik
Dergi 238: 3599-3618.
4.
Çelikoğlu
H.B., H.K. Cığızoğlu. 2007. Public transportation trip
flow modelling with generalized regression neural networks. Advances in Engineering Software 38(2):
71-79.
5.
Semeida A.M. 2014.
Derivation of travel demand forecasting models for low population areas: the
case of Port Said Governorate, North East Egypt. Journal of Traffic and Transportation Engineering 1(3): 196-208.
6.
Nuzzolo A, A.
Comi. 2014. Urban freight demand forecasting: a mixed
quantity/delivery/vehicle-based model. Transportation
Research Part E 65: 84-98.
7.
Yang Y. 2015.
Development of the regional freight transportation demand prediction models
based on the regression analysis methods. Neurocomputing
158: 42-47.
8.
Toole J.L., S.
Colak, B. Sturt, L.P. Alexander, A. Evsukoff, M.C. Gonzalez. 2015. The path
most traveled: travel demand estimation using big data resources. Transportation Research Part C 58:
162-177.
9.
Yang X.S. 2014. Nature-inspired Optimization Algorithms.
London and Waltham, MA: Elsevier.
10.
Turkish
Statistical Institute. Road traffic accident statistics. Available at:
http://www.tuik.gov.tr.
11.
Hlusička M., J.
Kraus, 2017. Increasing the usability of near-sea aerodromes. Nase More 64(2): 45-49.
Received 18.10.2017; accepted in revised form 12.01.2018
![]()
Scientific Journal of
Silesian University of Technology. Series Transport is licensed under
a Creative Commons Attribution 4.0 International License